Исследование свойств внутриглазного инородного тела на основе анализа рентгенографических изображений черепа

Актуальность работы обоснована необходимостью автоматизации процессов диагностирования и локализации внутриглазного инородного тела [1, 2]. Одной из основных причин неудачного или несвоевременного извлечения внутриглазного инородного тела (ВИТ) является некачественная диагностика из-за несовершенства диагностической техники, ошибок в проведении диагностических манипуляций, наличия мелких (менее 1,0 мм) осколков, не улавливаемым ультразвуком. Среди методов, с помощью которых можно определить локализацию ВИТ, наиболее широкое распространение получило рентгеновское исследование, в результате которого наблюдаются изображения рентгеновских проекций и по ним проводится оценивание различных характеристик и параметров, позволяющих сделать предположение об уточнённом диагнозе. Достоинствами метода является высокая информативность о взаимоотношении ВИТ и внутриглазных структур, быстрота и безболезненность исследования, возможность проведения его в ранние сроки после травмы, выявление материала инородных тел. Данная работа осуществляется совместно с Самарской клинической офтальмологической больницей им. Т.И. Ерошевского, где применяемый в настоящее время метод рентгеновского исследования, основанный на использовании стандартно-схемАтической модели глазного яблока, не позволяет использовать весь спектр возможностей высококачественного современного диагностического оборудования.

Согласно методике, используемой в Самарской клинической офтальмологической больнице им. Т.И. Ерошевского, диагностика ВИТ проводится по рентгенограммам, выполненным в двух проекциях: фронтальной и боковой. Расчёт положения ВИТ относительно оси глаза, расстояние его от наружной капсулы глаза осуществляется с помощью специальных расчётных сеток [3] с миллиметровыми делениями (рис. 1).

Перед приведением R-исследований на глазное яблоко пациента накладывается протез-индикатор со свинцовыми метками, которые служат ориенти- рами при расчёте на R-грамме положения ВИТ и его размеров (рис. 1).

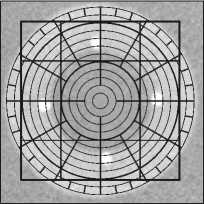
Рис. 1. Пример изображения типового снимка протеза-индикатора и расчётной сетки Горяева

Свинец используется в метках, поскольку он как тяжёлый элемент сильнее поглощает рентгеновское излучение и метки на изображении имеют большую яркость, чем окружающая их окрестность, поэтому чётко выделяются на рентгенограмме. Кроме того, эти метки, будучи геометрически расположенными на двух взаимно перпендикулярных прямых, образуют подобие системы координат, с помощью которой возможно определить в плоскости изображения координаты залегания ВИТ. Расчёт не является абсолютно точным из-за возможных погрешностей в укладке головы пациента и рентгеновской плёнки, а также из-за неполного контакта протеза-индикатора с глазным яблоком и его смещения. Итогом совместной с врачами работы является создание пространственной компьютерной модели внутриглазного инородного тела и параметрической модели глазного яблока с механизмом отслеживания временных изменений параметров на основе рентгенографических данных. Это позволяет спроектировать автоматизированные рабочие места врачей (АРМ хирурга-офтальмолога) с возможностью на дооперационном этапе проводить обнаружение ВИТ, определять его взаимоотношения с окружающими тканями глаза, корректировать объём хирургического вмешательства, прогнозировать его исход и автоматизировать работу кабинета медицинской статистики.

Задачей данной работы является определение зависимости соотношений значений функции яркости опорных маркерных точек протеза-индикатора и объекта на рентгенографическом изображении от набора начальных данных, определяющих интенсивность излучения. В состав данных входят: задаваемое в рентгеновском аппарате напряжение, сила тока на рентгеновской трубке, экспозиция (время излучения). Таким образом, может быть установлена непосредственная зависимость значения функции яркости отдельного элемента изображения ВИТ от интенсивности излучения.

Рассмотрим физическую сторону процесса – определение интенсивности рентгеновского излучения, прошедшего алюминиевый протез-индикатор и попадающего на фотоприёмник аппарата. Для решения задачи был рассмотрен закон Бугера (закон ослабления интенсивности), специфическая зависимость коэффициента поглощения от длины волны излучения и от природы вещества (т. е. атомного номера элемента или заряда ядра). Исходные данные представляют собой изображения в формате DICOM [4,5].

Взаимодействие рентгеновских лучей и вещества

Пучок рентгеновских лучей ослабляется при прохождении через вещество [6]. Взаимодействие излучения и вещества достаточно сложно – фотоны, не прошедшие через вещество вместе с пучком, могли претерпеть различные преобразования: а) они могли остаться фотонами, но изменить направление своего движения без потери энергии; это излучение, рассеянное без изменения длины волны; если имеет место небольшая потеря энергии, то это рассеяние с изменением длины, или «эффект Комптона»; б) фотоны могли быть поглощены атомами; это фотоэлектрический эффект. Возбуждённый атом испускает при этом два рода излучения: электроны и рентгеновские лучи, длина волны которых определяется не длиной первичной волны, а является характеристической для возбуждённого атома.

Мы рассмотрим суммарный эффект этих явлений, не анализируя подробно каждый отдельно, т. е. будем изучать поглощение рентгеновских лучей в веществе.

Поглощение рентгеновских лучей

Рассмотрим суммарное поглощение, вызываемое фотоэлектрическим эффектом и рассеянием [6,7]. Последняя причина поглощения к тому же незначительна по сравнению с первой, за исключением тех случаев, когда лучи с короткими длинами волн (но эти случаи остаются за пределами рассматриваемой нами области) проходят через лёгкие элементы.

Будем считать, что экран очень тонкий и однородный; пучок монохроматических лучей с сечением, равным единице, пересекая его, теряет энергию dI , пропорциональную пересечённой массе экрана на 1 см2 dp и первичной интенсивности пучка I . Запишем это в виде: dI = -nIdp, где П — коэффициент массового поглощения вещества экрана. Для экрана конечной толщины, интегрируя, находим, что отношение интенсивности падающего пучка к интенсивности прошедшего пучка зависит от массы на единицу поверхности p , пересечённой пучком, и определяется формулой I/10 = exp (-np), что равносильно I/10 = exp (-n5x), где x — толщина слоя, а 5 - плотность поглощающего вещества. Коэффициент массового вещества n постоянен для данного вещества, в каком бы физическом состоянии оно ни находилось. Коэффициент линейного поглощения Ц = П5 зависит от плотности экрана. Поглощение рентгеновских лучей веществом – явление атомное: для сложного вещества оно равно сумме поглощений всеми составляющими элементами и в первом приближении не зависит от характера связи между ними [6]. Причина этой зависимости в том, что рентгеновские фотоны, обладая высокой энергией, взаимодействуют с электронами внутренних оболочек, тогда как для видимого света имеют значение внешние электроны, состояние которых уже существенно зависит от характера межатомных связей.

Например, свинцовое стекло поглощает рентгеновские лучи тем сильнее, чем больше в нём свинца, но в то же время оно остаётся прозрачным для видимого света. Таблицы с коэффициентами поглощения элементов для разных длин волн достаточны для расчёта коэффициента поглощения любым веществом известного состава. В табл. 1 приведены его значения для алюминия и свинца в рассматриваемом диапазоне длин волн [6]:

Таблица 1. Значения коэффициентов поглощения

Элемент	Длины волн, ангстрем
	0,71	1,44	1,54	1,66	1,79	1,94	2,10	2,29
Al	5,3	40,0	48,7	58,4	73,4	92,8	117	149
Pb	141	202	241	294	354	429	499	585

Зависимость поглощения от длины волны

Показатель поглощения элемента является одновременно функцией рассматриваемой длины волны и атомного номера элемента. Увеличение ц происходит скачками, неравномерно: поглощение резко возрастает, когда длина волны, уменьшаясь, проходит некоторые постоянные величины, называемые порогами поглощения. Эти разрывы объясняются механизмом фотоэлектрического эффекта, т.е. поглощения фотонов атомами. Как только λ становится меньше λ K (предельная длина волны оболочки), поглощение слоем резко увеличивается, а затем постепенно убывает при дальнейшем уменьшении λ. Внутри одной области длин волн коэффициент поглощения приблизительно пропорционален Х 3 [6].

Зависимость поглощения от природы элемента

Будем считать постоянной длину волны. Для данного монохроматического излучения поглощение, вообще говоря, возрастает с атомным номером Z. Лёгкие элементы (органические вещества, алю- миний) поглощают достаточно слабо, тогда как тяжёлые элементы поглощают весьма сильно; хорошо известно, что для защиты от рентгеновских лучей используется свинец. Но увеличение поглощения по мере возрастания атомного номера не непрерывно, а происходит скачками; скачки эти вызываются теми же причинами, что и в предыдущем случае. Для области, заключённой между двумя скачками, коэффициент поглощения также приблизительно про-3

порционален Z , но этот закон менее строг, чем тот, который связывает ц и X .

Определение коэффициента поглощения

Используем эмпирические законы, связывающие ц с X и Z , для интерполяционного расчёта значений ц для различных элементов и длин волн. Согласно вышеизложенному, можно считать, что коэффициент поглощения пропорционален и произведению X ³ • Z ³: ц = C -X ³ • Z ³, где C - неизвестная константа. Её мы определим, взяв из таблицы несколько пробных значений длин волн и атомных номеров интересующих нас элементов – алюминия и свинца. В результате получим приближённое значение:

C = 0,00619052 • 10³⁰ м ^- 4 = 6,19052 • 10 ^{- 13} ( Е ) — 4 .

Расчёт интенсивности

Вычислим далее интенсивность рентгеновского излучения, прошедшего через алюминиевый протез и падающего на фотоприёмник, для чего используем закон ослабления интенсивности. Поскольку этот закон определён для конкретной длины волны, а мы имеем целый набор, то интенсивность будет находиться как интеграл:

X 2

I = j I0 [X]- exp (-ц(X, Z) x) dX =

X i

^X 2

= J10 [X]- exp (-CX3Z3x) dX, Xi где 10 [X] - заданное дискретно начальное распределение интенсивности по длинам волн (спектр), X1, X2 - нижняя и верхняя границы спектра, x -толщина протеза, Z – атомный номер элемента вещества, через которое проходит излучение.

Если вещество состоит из N элементов, то в по-

N казателе экспоненты берут сумму: ^цjxj. В дан-j=i ном случае у нас протез состоит из двух видов элементов: алюминия (Al) и свинца (Pb), поэтому:

^X 2

I = J I 0 [ X ] - exp ( - C X ³ [ Z A _zx A _; + Z p _bX p _b ] ) d X ,    (2)

Xi где X1 =( hc)/(eU), (U - известное напряжение трубки), X2 = 1,39 A - верхняя граница спектра (она также известна из экспериментально найденного распределения). Необходимые данные для расчёта: толщина алюминиевого протеза: xAl = 1 мм, толщина слоя свинца: xPb = 0,2мм . Все значения I0 [X] считаются известными из экспериментального графика, который представлен на рис. 2.

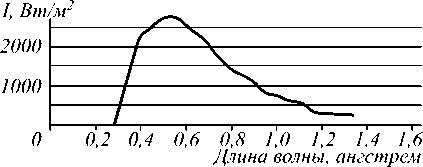
Рис. 2. Распределение интенсивности

Это непрерывный спектр излучения рентгеновской трубки (напряжение 40 кВ).

Применим соответствующим образом масштабные коэффициенты к данному графику по напряжению и силе тока.

Поскольку нижняя граница диапазона длин волн зависит от напряжения, то в соответствии с вводимым значением U_new длина волны будет равна X 1 • UjU nw . Известно также, что максимум спектра составляет X _max = ( 32 ) X 1 . Интенсивность I будет масштабироваться по току, как I • i nw/ i , и по квадратам напряжений, исходя из энергетических соображений, как I • ( U new/ U ) 2 , поскольку суммарная энергия также пропорциональна U ² . Таким образом, мы можем для различных значений напряжения U и тока I находить интенсивность.

Рассчитаем интенсивность пучка ( I ₁ ), проходящего только через вещество свинца, по формуле (2), положив в ней x_Al = 0 (рис. 3).

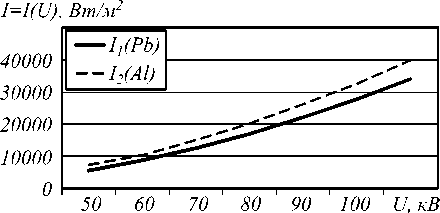
Рис. 3. Зависимость значения интенсивности от напряжения для различных материалов

Значения интенсивности I ₂ , найденные по формуле (2) при x_Pb = 0 , определяют интенсивность пучка, проходящего только через вещество алюминия.

Проведём аналогичные операции для вычисления интенсивности, как и в предыдущем случае, но при постоянном напряжении на трубке U = 110 кВ и меняющемся токе. Рис. 4 – для зависимости интенсивности от тока по той же формуле (2):

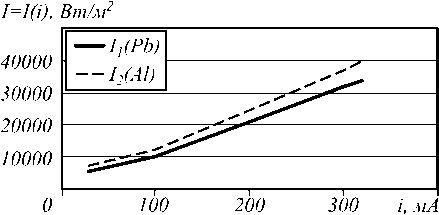
Рис. 4. Зависимость значения интенсивности от силы тока при постоянном напряжении U = 110 кВ

Таким образом, мы, построив данные зависимости, приходим к выводу, что с увеличением как тока, так и напряжения интенсивность излучения увеличивается, причём в первом случае оно линейное, во втором – почти квадратичное. Это подтверждает, в частности, представление о том, что суммарная энергия излучения пропорциональна квадрату напряжения.

Определение параметров ВИТ

Для анализа свойств ВИТ необходимо определить средний атомный номер элементов, из которых он состоит [6]. Если наблюдаем объекты одного и того же размера, имеющие разный средний атомный номер и различную яркость на изображении, то ВИТ, средний атомный номер которого больше, будет темнее. Таким образом, сопоставив яркость наблюдаемого ВИТ с яркостями объекта известного нам материала, мы сможем определить средний атомный номер, а значит, и физические свойства объекта.

Обработке подвергались рентгенографические изображения алюминиевого протеза, представленные в медицинском формате DICOM. Съёмка проводилась при варьировании в некоторых пределах параметров установки – тока, напряжения и экспозиции.

Алгоритм анализа изображения заключался в оценке средней яркости по конкретным характерным областям (по маркерным точкам и непосредственно по «кольцу» протеза-индикатора). Также необходимо найти величину, при которой спектр (распределение по частотам) интенсивности оставался бы неизменным и которая определялась бы поглощением излучения. Согласно закону поглощения – закон Бугера: ln(I/10) = -(цAlxAl +ЦPbxPb), где x — толщина материала. Таким образом, этой величиной является логарифм отношения интенсивностей после и до поглощения, т.к. он пропорционален коэффициенту поглощения, т.е. может определять поглощающие свойства. В дальнейшем удобнее использовать в качестве оценки отношения интенсивностей отношение значений функций яркости: k = ln (f/fo ) = -px, т.к. между ними прямая моно- тонная зависимость, и подтвердим это экспериментально. В формуле обозначено: F – среднее значение функции яркости для кольца протеза, а F0 – среднее значение функции яркости маркера. Коэффициент связывает яркость двух наблюдаемых объ- ектов на изображении и позволяет определять свойства одного объекта на основе свойств другого наблюдаемого объекта.

В результате эксперимента, заключавшегося в получении (при различных напряжениях) и дальнейшей оцифровке снимков протеза, были определены значения функции яркости отсчётов всего кольца и маркерных точек DICOM изображений. В последнем столбце табл. 2 подсчитан логарифм отношения значений функций яркости кольца и маркера для соответствующего значения напряжения. Здесь сила тока постоянна и равна I =320 мА, параметр яркости – логарифм отношения яркостей кольца и маркера (рис. 5 а , б ).

Таблица 2

№	U , кВ	Значение функции яркости кольца	Значение функции яркости маркера	Параметр k
1	50	41,15	14,66	1,032
3	70	44,66	17,15	0,957
5	90	64,40	26,84	0,875
7	110	112,41	49,39	0,822

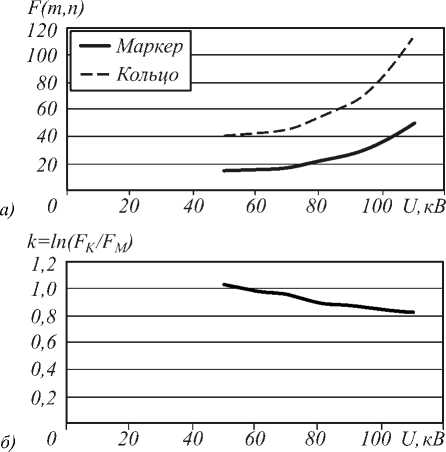
Рис. 5. Зависимость от напряжения яркости для различных объектов (маркера и кольца) (а), параметра k (б)

В табл. 3 приведена зависимость яркостей тех же областей, что и в предыдущем случае, от значения силы электрического тока при постоянном напряжении U = 110 кВ.

Таблица 3

№	i , мА	Значение функции яркости кольца	Значение функции яркости маркера	Параметр k
1	320	111,00	49,39	0,819
2	250	95,55	42,15	0,820
3	200	82,62	36,38	0,820
4	160	74,45	32,73	0,821
5	100	69,08	30,39	0,821

Графики для значений яркости и величины логарифма отношения яркостей приведены на рис. 6 а , б соответственно.

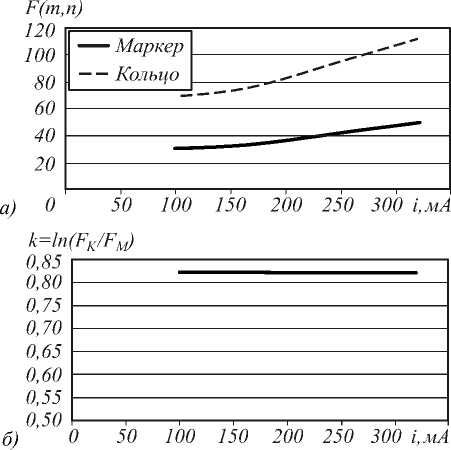
Рис. 6. Зависимость от силы тока яркости для различных объектов (маркера и кольца) (а), параметра k (б)

Анализируя полученные графики, сделаем следующие выводы. График на рис. 5 а показывает, что с ростом напряжения абсолютное значение функции яркости возрастает (визуально сравнивая с теоретической, можно сказать, что зависимость квадратичная); на рис. 5 б видно, что величина разности логарифмов яркостей кольца и маркера постепенно убывает, поскольку спадает поглощающая способность излучения и увеличивается его проникающая способность.

Абсолютное значение функции яркости с ростом силы тока практически линейно возрастает (при неизменном напряжении), что отражено на рис. 6 а , а величина логарифма отношения яркостей остаётся почти постоянной (это видно на рис. 6 б ), поскольку спектр (распределение) не меняется. Это говорит о том, что измерения, полученные на практике, хорошо согласуются с теорией, в данном случае – с законом поглощения.

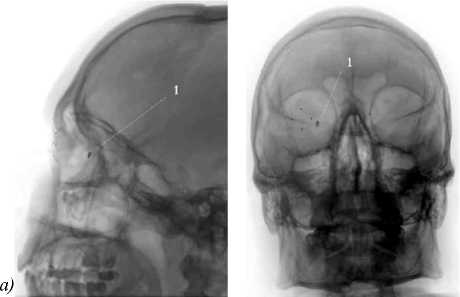
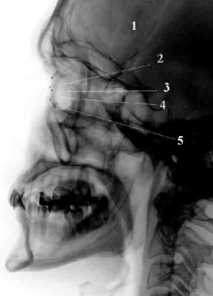
Полученные результаты применимы к реальным изображениям для определения свойств внутриглазного инородного тела, исходя из значений функции яркости этого объекта. Проанализируем следующие оцифрованные снимки: с изображением головы пациента, протеза-индикатора, ВИТ для определения свойств ВИТ, найдя его яркость и яркость маркерных точек. На рис. 7 представлены изображения головы пациента в профильной и во фронтальной проекциях (а – 184.dcm, 673.dcm: цифрой 1 обозначено ВИТ, б –764.dcm, 667.dcm: маркерные точки: цифры 1-4, ВИТ – цифра 5).

Вычислим средние значения абсолютных величин значений функции яркости маркерных точек и ВИТ и параметр k . Напряжение считается постоянным и равным U = 110 кВ (табл. 4).

Таблица 4

Изо-браже-ние	Значение функции яркости маркера	Значение функции яркости ВИТ	k	Вид проекции
764.dcm	46,94	75,54	0,476	фронтальная
667.dcm	47,00	93,57	0,688	профильная
184.dcm	76,99	124,93	0,484	профильная
673.dcm	69,62	83,17	0,178	фронтальная

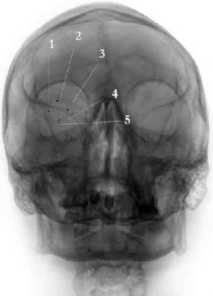
Анализируя полученное значение k и известные значения функции яркости маркерных точек при заданных значениях напряжений, силы тока и времени экспозиции, можно сделать выводы о физических свойствах инородного тела.

Таким образом, в результате исследования можно сформировать алгоритм анализа свойств инородного тела, который в дальнейшем можно использовать в задаче автоматического распознавания ВИТ на рентгеновских снимках:

• 1.    Используем изображение во фронтальной проекции, так как внутри области глаза фон можно считать однородным.

• 2.    Оцениванием среднее значение функции яркости по характерным областям DICOM изображения (маркер и ВИТ) (рис. 8).

• 3.    Оцениванием параметр k , как натуральный логарифм отношения функции яркости F ( m , n ) маркеров и ВИТ.

• 4.    Анализируем полученное значение параметра k на графике (рис. 5 б ), который показывает распределение характеристической кривой для свинца (маркеры). Если параметр k лежит ниже кривой, то ВИТ соответствует либо свинцу меньшей толщины, либо материалу меньшей поглощающей способности. Если известен материал ВИТ, то можно оценить его толщину. Если по двум проекциям произведена оценка толщины ВИТ, то можно определить средний атомный номер материала.

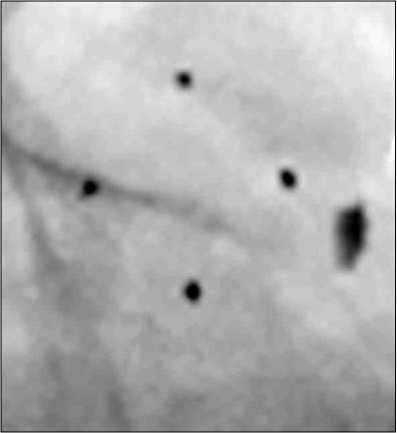
Рис. 8. Характерные области рентгеновского изображения (маркеры и ВИТ)

Заключение

Экспериментально установлен факт пропорциональности между интенсивностью излучения и функцией яркости отсчётов изображения. Предложен способ определения общих свойств внутриглазного инородного тела, основанный на соотношениях яркостей отсчётов на рентгенограмме и на экспериментальных кривых зависимости яркости. Выведена величина, определяемая поглощением (логарифм отношения яркостей характерных областей), согласно которой можно определить физические свойства инородного тела (средний атомный номер материала), зная его значение функции яркости. Если известен материал ВИТ, то можно оценить его толщину.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), гранта

Президента РФ поддержки ведущих научных школ (НШ-3086.2008.9), программы Президиума РАН «Фундаментальные науки – медицине», гранта РФФИ 10-07-00341-а, государственного контракта № 02.740.11.0841.