Исследование технического состояния как фактора надежности технологической системы металлорежущего станка

вость металлорежущего станка оказывают деформации элементов эквивалентной упругой системы ( X нс , X гд , X nn ) в направлении подачи стола, поэтому целесообразно в качестве диагностических параметров использовать динамические характеристики, определенные в этом направлении.

Учитывая положение, передаточная функция эквивалентной упругой системы:

^WЭУС ⁽ Р ) = W HC ⁽ Р ) + W rn ⁽ Р ) + W nn ⁽ Р ) ' (1) где W_HC ( Р ) , W_rn ( Р ) , W _nn ( Р ) — передаточные функции соответственно НС, главного привода, привода подач, рассматриваемых как параллельно соединенные элементы.

Передаточная функция разомкнутой системы:

W PA3 ⁽ Р ) = W 3YC ⁽ Р ) ¹ W nP ⁽ Р ) , (2) где W nP ( Р ) – характеристика процесса резания, учитывающая изменение настройки.

Если рассматривать главный привод как одномассовую колебательную систему, то его передаточная функция запишется в виде:

Wrn(P) = т2 2 т 1’     (3)

T 2 Р + T 1 р + 1 ^v ’ где T_г и T 1 — инерционная постоянная и постоянная времени демпфирования соответственно; q – приведенная крутильная податливость; W rn ( Р ) необходимо привести к поступательным перемещенным в направлении оси ОХ подачи стола

у

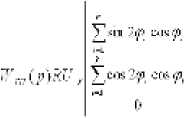
У «in ?» пп I».   11

У<0«2^> II H (? I где R и k – радиус и число зубьев фрезы; U x – изменение толщины среза по оси ОX в плоскости, проходящей через ось фрезы; pi - угол, определяющий положение зуба фрезы относительно точки входа его в заготовку.

Приведенная передаточная функция w n ( p ) отражает взаимосвязь между единичным изменением вектора силы и суммарным изменением толщины среза из-за закручивания главного привода [2].

Передаточная функция привода подач с учетом характеристики жидкостного трения в направляющих и упругости привода [3]:

w ч- ) =

______________^р+1______________ в, mp +(в,в3 + m+в,ву)р2 + (в2 + в, к - в)р+c

(5) где в – наклон статистической кривой трения, соответствующий рассматриваемой скорости подачи; в , и в — постоянные времени всплывания стола и жидкостного трения; в 2 — постоянная демпфирования в механической части привода; m и c – приведенные масса стола и коэффициент жесткости привода.

НС станка обычно моделируют многомассовой системой с упругими и диссипативными связями. Число масс можно определить по экспериментальным АФХЧ НС, исходя из количества резонансных состояний в рассматриваемом частотном диапазоне возмущений. Экспериментальные исследования динамических характеристик гаммы тяжелых вертикально-фрезерных станков производства УЗТиФС (мод.654, 6560, 6560МФЗ) показали, что АФЧХ НС имеют три явно выраженных резонансных состояния (рисунок 2). Это обусловлено упругими связями: станины с основанием ( f , = 25 Гц ) , стойки и шпиндельной бабки ( f 2 = 45 Гц ) , стойки и станины ( f 3 = 62 Гц ) . Возмущающее воздействие создавалось вибратором, варьирование амплитуды возмущающего воздействия при определении АФХЧ показало квазилийность НС в направлении подачи стола. Исходя из этого, динамическую модель НС можно представить в виде трехмассовой линейной системы с упругими и диссипативными связями (рисунок 3).

Здесь m , - приведенная масса станин и стола; m ₂ и m ₃ - массы стойки и шпиндельной бабки соответственно; C , , C 2 , С ₃ - приведенные коэффициенты жесткости связей; к , , к 2 , к 3 -коэффициенты демпфирования; x , , X 2 , X ₃ -перемещения соответствующих масс в направлении подачи стола; р ( t ) - возмущающее воздействие процесса резания.

Дифференциальные уравнения движения масс:

m₁x ₁ + c ₂( X — x ,) + к , х + к ₂( x — x) = P(t );               !

m 2 x ₂ + c ₂( x ₂ - x ) + к 2 (x ₂ - x ) + c ₃( x - x , ) + к , ( x - x) = 0; > (6) m3x + c ₃( x - x) + к 3 (x - x ₂) = Pt ).

Для определения АФЧХ НС воспользуется методом механического импеданса, учитывая гармонический характер возмущающего воздействия и линейность системы. Заменяя в системе уравнений (6) P (t), x, (t), x 2 (t), x 3 (t) соот-itot      iHDt      iUDt      iUDt

0 e , x, e , x 2 e    , x 3 e    , где P0 - амплитуда возмущений; x,, x2, x3 -амплитуды колебаний масс.

После соответствующих преобразований получим систему алгебраических уравнений отно- сительно x,, x2, x3

x , ( c , + c ₂ - m , to ² + ik , to + ik ₂ to ) - x ₂ ( c ₂ + ik ₂ to ) = P ₀;

- x , ( c 2 + ik 2 ® ) + x 2 ( c 2 + c 3 - m 2 ® + ik 2 ® + ik 3 ® ) -

- x ₃ ( c ₃ + ik ₃ ® ) = 0;                                    (7)

- x ₂ ( c ₃ + ik ₃ ю ) + x ₃ ( c ₃ - m ₃ ® ² + ik ₃ ® ) = P ₀

Разделим уравнение системы (7) на P 0 и представим его в каноническом виде:

A,, x, + A,2 x 2 + A,3 x3 = ,;

A 2, x, + A 22 x 2 + A 23 x 3 = 0:

A 3, x, + A32 x 2 + A 33 x3 = ,,

где

A ,, = [( c , + c ₂ - m to 2 ) + i ( к , ® + к ₂ to )], / P ₀;

A , ₂ = ( - c ₂ - ik ₂ to ), / P ₀;

A ,3 = 0;

A ₂ , = ( - c ₂ + ik ₂ to ), / P ₀;

A ₂₂ = [( c ₂ + c ₃ - m ₂ to ²) + i to ( к ₂ + к ₃)], / P ₀;

A ₂₃ = ( - c ₃ - i to k ₃), / P ₀;

A 3, = 0;

A ₃₂ = ( - c ₃ - ik₃ to ),/ P ₀;

A ₃₃ = [( c ₃ - m ₃ to ²) + ik ₃ to ], / P ₀.

Решение системы уравнений (8) ищем в виде

x, = A, / A; x2 = A2 / A; x3 = A3 / A, (9) где

	AH	A ,2	0		,	A ,2	0
A =	A ,2	A 22	A 23	;            A , -	0	A 22	A 23
	0	A 23	A 33		,	A 23	A 33
	A ,,	,	0		AH	A ,2	,
A 2 =	A ,2	0	A 23	;            A 3 -	A ,2	A 22	0
	0	,	A 33		0	A 23	,

• - комплексные определители системы (8) АФЧХ НС запишется в виде:

Whc(ito) = (x -x3)/Po.     (10)

Амплитуда и фаза относительных колебаний стола и шпиндельной бабки в направлении подачи под действием единичной возмущающей силы может быть найдена из соотношений:

Ahc =

НС

J [( А - А 3 ) А o + ( В 1 - В 3 ) В о ] ² + [( В , - В 3 ) А о - ( А - А 3 ) B 0F .

А о2 + Во2                            ’ ф нс = arctg

Bi An - A₀B₀ -A—⁰---—- - arctg

A 1 A 0 - B , B 0       ^S

B 3 A 0 - A 3 B 0

A 3 A 0 - B 3 B 0 ’

где A ₀; B ₀; A , ; B 1 ; A ₃; B ₃ - соответственно действительные и мнимые части комплексных определителей A ; A , ; A ₃.

Характеристика процесса резания при торцевом фрезеровании W _np ( p ) , учитывающая периодические импульсные возмущения при выходе нагруженного зуба из металла и колебания скорости резания, может быть определена из соотношений, приведенных в работе [4]. В первом приближении можно воспользоваться общепринятой передаточной функцией процесса резания, соответствующей периодическому звену:

W_nP ( P ) = k P /1 + T P P , ⁽¹²⁾ где T_P – постоянная времени стружкообразова-ния; k _P – статическая характеристика процесса резания.

Представление W ПР ( p ) в виде (12) справедливо только при устойчивом стружкообра-зовании.

Для проверки адекватности полученной динамической модели объекту, была рассчитана динамическая характеристика НС по связи с процессом резания для станка модели 6560МФЗ.

Параметры динамической системы определились экспериментально на реальном объекте. Коэффициенты жесткости c_i находились путем линеаризации кривых нагружения основных элементов НС при статистических испытаниях на жесткость. Собственные частоты f_i определяем по экспериментальной АФЧХ (см. рисунок 2), полученной при воздействии вибратором. Приведенные “парциальные” массы рассчитываем по соотношению:

mt = Ci /!(2nfi )2. (13)

Также по экспериментальной АФЧХ определяем коэффициенты сопротивлений k _i :

k i = 2mm i V ® O i ^- to pi , ⁽¹⁴⁾ где to pi = 2 n f - собственная круговая частота; to pi - резонансная частота.

Чистовые значения параметров динамической системы сведены в табл. 1.

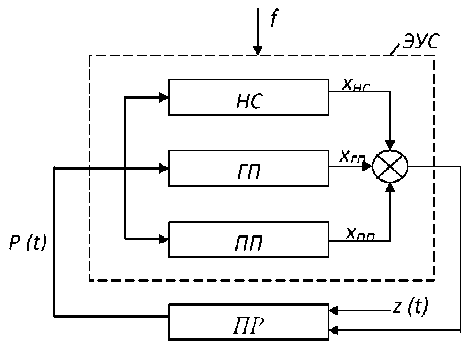
Рис. 1. Схема динамической системы вертикально-фрезерного станка

Таблица 1. Структурные параметры динамической системы станка модели 6560МФЗ

m ,	c 1	k 1	m 2	c 2	k 2	m 3	c 3	k 3
кг	кг / с2	кг / с	кг	кг / с с	кг / с	кг	кг / с 2	кг/ с
8110	200*106	787*103	5450	435*10 6	530*103	997	1511*10 6	284*103

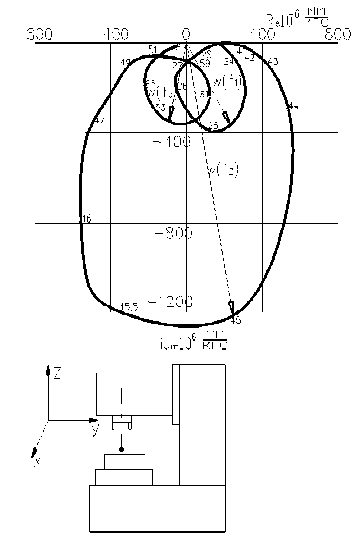
Рис. 2. Экспериментальная АФЧХ станка модели 6560МФ3 в направлении подачи стола при воздействии вибратором

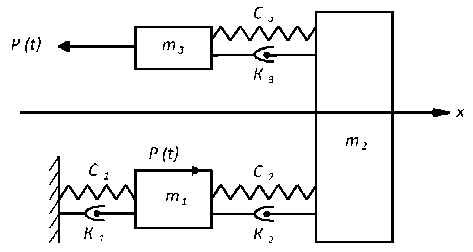
Рис. 3. Динамическая модель несущей системы станка-стенда фрезерного станка

Сравнение экспериментальной АФЧХ с расчетной, полученной по приведенным выше зависимостям на ЭЦВМ показали их хорошее совпадение. Расхождения по амплитуде не превышало 20%, по фазе 25% (рис. 4), что позволяет использовать динамическую модель станка для задач диагностики.