Исследование текстурных признаков для диагностики заболеваний костной ткани по рентгеновским изображениям

Остеопороз – это системное заболевание, поражающее все кости скелета, сопровождающееся снижением плотности и прочности костной ткани, а также нарушением её структуры, что приводит к высокому риску переломов даже при небольшой травме. Остеопения – это лёгкая форма остеопороза. Для предупреждения переломов важно как можно раньше поставить правильный диагноз, чтобы назначить лекарственные средства, замедляющие развитие заболевания [1, 2].

Стандартным средством диагностики остеопороза является процедура денситометрии, основанная на измерении минеральной плотности костной ткани. К сожалению, для этого требуется дорогостоящая аппаратура, которая в российских клиниках в настоящее время распространена очень слабо.

С другой стороны, имеется метод субъективной диагностики остеопороза по рентгеновским снимкам определённых областей интереса, на которых хорошо заметны изменения в так называемой трабекулярной структуре костной ткани [3]. Например, на рис. 1 а и 1 б видно, как меняется структура шейки бедра, поражённой остеопорозом: на втором изображении структура выглядит более прозрачной, волокнистой, редкой.

Общая проблема субъективной диагностики заключается в отсутствии средств автоматизации этого процесса. В свете этого возникает задача разработки компьютерных методов такой диагностики, что позволило бы ускорить её и сделало более доступной не только узким специалистам, но и специалистам широкого профиля. Кроме того, такой подход значительно дешевле использования специализированного оборудования для денситометрии и мог бы применяться повсеместно.

Основная идея, на которой построена работа, – использовать текстурные признаки для оценивания целостности структуры трабекул по рентгеновским снимкам шейки бедра, что может производиться программно, без участия квалифицированных спе- б)

циалистов.

а)

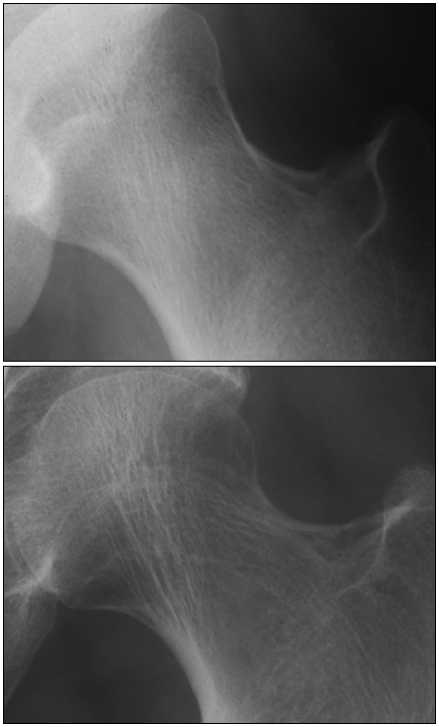
Рис. 1. Рентгенограммы шейки бедра: здорового человека (а), страдающего остеопорозом (б)

В зарубежных изданиях описаны некоторые попытки использовать отдельные группы признаков, например, маски Лоу [4], признаки Харалика [5], спектральные характеристики [6], вейвлет-ана- лиз [7], для описания трабекулярной структуры костной ткани. Однако сравнение эффективности различных признаков для решения задачи автоматической диагностики и отбор оптимальной группы признаков не проводились.

1.    Регистрация изображений и предварительная обработка

Для получения физических снимков используется аналоговая запись изображения на рентгеночувствительную плёнку, которая впоследствии подвергается сканированию. Область снимка включает тазобедренный сустав и шейку бедра.

Разрешение таких изображений до сканирования, по сути, зависит от разрешения рентгеночувствительной плёнки. В данном исследовании используется плёнка KodakMedical X-Ray Film General Purpose Green (MXG). Её разрешающая способность составляет примерно 16 линий на мм или 400 точек на дюйм.

С нашей точки зрения, изображение на плёнке можно рассматривать как функцию x 0 ( 1 1 , 1 2 ) , возвращающую яркость изображения в точке с координатами ( 1 1 , 1 2 ) . Изображение ограничено, то есть 0 <  1 1 <  1 1 и 0 <  1 2 <  l 2 . Оно монохромное, то есть имеет только один канал яркости – оттенки серого.

Полученные физические фотографии подвергаются сканированию, причём разрешение при этом не теряется. Можно считать, что в процессе оцифровки непрерывное изображение x ₀ ( 1 1 , 1 2 ) последовательно подвергается двум преобразованиям: дискретизации и квантованию, в результате чего получается двумерное дискретное изображение x ( m , n ), состоящее из M х N отсчётов (0 <  m <  M и 0 <  n <  N ). Каждый отсчёт характеризует уровень яркости и принимает целочисленные значения от0 до L - 1 = 255 включительно.

В порядке предварительной обработки изображения ориентируются, на них локализуется область интереса. От дополнительных преобразований, таких как контрастирование и фильтрация шумов, было решено отказаться, чтобы не потерять информацию, потенциально содержащуюся на изображении. Кроме того, на изображении x ( m , n ) специалистом выделяется полигональная область D x , включающая только трабекулярную структуру.

2.    Текстурные признаки

Моменты функции яркости

Допустим, что имеющиеся участки изображений – реализации двумерных стационарных случайных полей. Тогда можно говорить о центральных и начальных моментах как о постоянных величинах, не зависящих от номера отсчёта на изображении [8]. В предположении об эргодичности их состоятельные оценки могут быть посчитаны по отсчётам функции яркости изображения [9].

В данном исследовании были использованы следующие признаки на основе моментов функции яркости: средняя яркость x , средняя энергия (1), среднеквадратическое отклонение о , коэффициент асимметрии, коэффициент эксцесса.

• ⁵    = ,1 S ^x 2 ⁽ m , n ).

I D x\ ( m , n ) e D x

Корреляционные характеристики

Часто в качестве текстурных признаков используют отсчёты выборочной нормированной корреляционной функции [10]:

R ( m , n ) =

S   x (i, j) x (i + m, j + n)

(i -j)6 Dx (m, n)____________________________________________ s\Dx ( m, n )| где Dx ( m. n )={( i. j k Dx l( i + m. j + n k Dx } .

Во многих источниках рекомендуется использовать именно такую корреляционную функцию без вычитания математического ожидания, так как колебания непосредственно функции яркости более информативны, чем её сдвиг относительно среднего значения, который может быть вызван, например, неравномерной освещённостью изображения [10, 11]. В ходе исследований использовались 8 отсчётов такой функции: для двух расстояний и четырёх направлений.

Признаки Габора

Двумерная функция Габора определяется как

00  0  0

G ( ¹ 1 , ¹ 2 ; ¹ 1 , ¹ 2 , ^to 1 , ^to 2 )

f ( t 1 — t 10 ) ( t ² — t 2 )

I    2 о2   ⁺   2 о2

e I

I + i ( to 0 1 1 +Ш0 1 ₂

)

. (2)

Произвольный двумерный сигнал x ₀ ( 1 1 , 1 ₂ ) может быть представлен в виде разложения по таким функциям:

a ( 1 10 , 1 20 , o> 0 , ® 0 ) =

+^ +^

= J j x 0 ( 1 1 , 1 2 ) G ( 1 1 , 1 2 ; 1 0 , 1 20 , ® ° , ® 2 ) d 1 1 d 1 2 .

-^ —^

Фурье-образ функции Габора (2) выражается в виде [10]:

(G (ц , ® 2 ; 1 1 ⁰, 1 0 , ® “ , ® ° , O 1 , 0 2 ) =

22       .

— о2 ^-W0 +02 to.-to0          _m0L0+/flY,_m0L0\

2 1 1^ 1/ 2\ 2 2/ I i ( ( to] 0) 1 ) ¹ 1 ⁺ ( ^2 ^2 ) ¹ 2 )

= 2 П0 1 0 2 e ^{v                 y}e

Используя Фурье-образ x_Q ( 1 1 , 1 ₂ ) сигнала x ₀ ( 1 1 , 1 ₂ ) , можно переписать разложение (3) в частотной области [10]:

a ( 1 10 , 1 0 , ® 0 , ® 0 ) =

+^ +^

= J J x ₀ ( 1 1 , 1 ₂ ) G ( 1 1 , 1 ₂; 1 10 , 1 ₂⁰, ® 0 , ® 2 ) d 1 1 d 1 ₂.

-^ -^

Это преобразование можно интерпретировать как поточечное умножение Фурье-образа сигнала на гауссовское окно с последующим обратным преобразованием Фурье. Именно эта идея используется на практике.

Рассмотрим дополненный нулями дискретный сигнал x (n1, n 2) =

I x ( n 1 + n 0 , n ₂ + n 0 ) , ( n 1 + n 0 , n ₂ + n 0 ) е D_x ; (4)

• 10 ,                       (n. + n0,n2 + n0)? D.

1       1      2       2 X

Здесь n 0 и n 0 - левая и нижняя границы множества D_x соответственно. Функция x ( n 1 , n ₂ ) определена для n 1 е { 0,1,..., M - 1 } и n ₂ е { 0,1,..., N - 1 } , где M - 1 и N - 1 - правая и нижняя границы множества D_x соответственно.

Над этим сигналом выполняется преобразование Фурье, и полученный образ поточечно умножается на заранее заданные гауссовские окна вида

| ( m 1 - m 0 ( k ) ) ( m ₂ - m 0 ( k ) ) | I 2 02 ( к )           2 02 ( к ) I

W k ( m 1 , m ₂ ) = e ^v                     ' .

В результате имеем набор комплексных изображений спектров исходного изображения, на каждом из которых выделена определённая область частот:

Уk (m1,m2 ) = X(m,,m2)(Wk (m1,m2) + Wk (m1,m2)), где окно Wk (m1, m2) имеет центр (-m0 (k),-m0 (k)), чтобы полученный спектр всё ещё соответствовал вещественным изображениям. Признаками будем считать средние энергии этих изображений [10], аналогичные (1):

+1

1        L 2 J       L 2 J gk=г,<   2     2 у k (m1,m 2)уk (m1,m 2).

MN     Г m - 1 1    Г N - 1 1

mi

Разобьём частотную область на прямоугольные участки, как показано на схеме (рис. 2).

в	14	7	2	8	15	16
9	10				11	12
3		4		5	б
1			0	1
6		5	2	4	3
12	11	8		7	10	9
16	15				14	13

Рис. 2. Разбиение спектральной области для выбора центров гауссовских окон

Центры гауссовских окон ( m ₁⁰( k ), m 0 ( k )) поместим в центры соответствующих участков, а параметры o 1 ( k ) и o ₂( k ) зададим как половины соответствующих линейных размеров этих участков. Такое разбиение позволяет лучше отличать высокочастотные текстуры [10].Таким образом, имеем 17 признаков Габора.

Признаки Харалика

Рассмотрим P d ₆ ( i , j ) - вероятность того, что два отсчёта функции яркости, находящиеся на расстоянии d в направлении 6 друг от друга, имеют цвета i и j . Положим

D d„ d 2 ( i , j ) =

= { ( m , n ) e D_x ( d 1 , d ₂ ) | { x ( m , n ) , x ( m + d 1 , n + d ₂ ) } =

= { i, j}} ,

тогда эти вероятности могут быть оценены как

P d б ( i , j ) = ”

D ( i , j ) D x ( d ,0 )

D 0#, d ( i , j ) D x ( 0, d ) ",

D d d ( i , j ) D x ( d , d )' ’

D + d , - d ( i , j ) D x ( ^{+ d} , ^{- d} )

6 = 0;

6 = ^П

6=+ 4

6=

П

.

Здесь i и j могут принимать значения от 0 до L - 1 включительно. Для фиксированных d и 6 (далее эти индексы опущены) могут быть рассчитаны 14 признаков Харалика [12]: второй угловой момент, контраст Харалика, корреляция Харалика, дисперсия Харалика, обратный разностный момент, суммарное среднее, суммарная дисперсия, суммарная энтропия, энтропия, разностная дисперсия, разностная энтропия, первая информационная мера корреляции, вторая информационная мера корреляции, максимальный коэффициент корреляции.

В данном исследовании использовалось два расстояния и четыре направления, так что всего рассчитывалось 112 признаков Харалика. Дополнительные сведения об этих признаках и способах их быстрого вычисления можно найти в [13].

Признаки Тамуры

Имеются 6 признаков, признанных существенными для зрительного восприятия в результате психологического эксперимента [14]. Все они вычисляются по эвристическим процедурам и никак не масштабируются.

• - Зернистость - это признак, связанный с расстоянием между заметными пространственными колебания-

• ми оттенков серого, то есть с размером примитивных элементов (текстелей), формирующих текстуру.

  – Контраст Тамуры – это мера того, насколько сильно и резко может меняться цвет на изображении.

  – Направленность – это признак, измеряемый с помощью гистограммы локальных направлений контуров.

  – Линейность – это признак, показывающий, насколько прямолинейны контуры на изображении.

  – Регулярность – это общая изменчивость первых четырёх признаков между различными частями изображения.

  – Грубость – субъективная оценка грубости переходов на изображении.

3.    Экспериментальные исследования

Эти признаки вычисляются по достаточно сложным эвристическим процедурам, описание которых выходит за рамки данной статьи.

За время выполнения исследования в клиники Самарского государственного медицинского университета с подозрением на остеопороз поступило 50 пациентов. Каждому с помощью денситометрии был поставлен один из трёх диагнозов: остеопороз, остеопения или без патологий. Кроме того, были получены рентгеновские снимки шейки бедра каждого пациента, они были оцифрованы и использовались как входные данные, наряду с известными диагнозами.

Для каждого из пятидесяти изображений были посчитаны все 148 имеющихся признаков. Далее полученные векторы признаков были случайным образом разделены на две выборки: обучающую и контрольную.

Для отбора признаков использовалась упрощённая процедура, подобная описанной в [16]. Изначальным показателем качества признаков выбран критерий дисперсионного анализа.

Пусть имеется обучающая выборка U е К K ^{х х}, где U_ij – значение i -го признака для j -го вектора из обучающей выборки. Относительно каждого вектора-столбца признаков U j е К K известен его класс Ф ( U j ). Вычислим значения оценок внутриклассовых дисперсий

D ⁽ l ) ( ^k ) = 17 I ( U j - M ( l ) ( ^k ) ) 2 ,

• ^V 1 / Ф ( U j ) = 1

где D ^{( 1} ) ( k ) - дисперсия k -го признака внутри 1 -го класса ( l принимает значения 0,1,2 для нормы, остеопении и остеопороза соответственно),

V =^ j е { 1,2, _ , V } Ф ( U j ) = 1 }| - количество векторов класса l в обучающей выборке,

M ^{( 1} ) ( k ) = — I U_kj - среднее значение признака

• ^V 1 j Ф ( Uj} = 1

k внутри l -го класса.

Среднее значение среди внутриклассовых дисперсий характеризует рассеяние соответствующего признака относительно средних значений классов:

D ^W( k ) = 1 1 D ^{( 1} ) ( k ) .                         (5)

³ 1 = 0

Кроме того, определим значение оценки дисперсии смеси распределений:

V 2

D ( ^k ) = 7 1 ( U kj - ^{M w}( ^k ) ) , ^V j = 1

V

где M w( k ) = -1 Uj

^V j = 1

среднее значение k -го

признака по всем элементам обучающей выборки.

Признак тем более информативен, чем лучше он разделяет классы. То есть лучшими признаками яв- ляются те, у которых отношение дисперсии смеси (6) к средней внутриклассовой дисперсии (5) больше. Таким образом, признаки нужно отсортировать в порядке невозрастания следующего критерия:

J ( ^k ) =

D ( ^k ) D ^(z) ( k )

после чего оставить только несколько первых.

В табл. 1 приведены десять лучших по критерию (7) признаков. Видно, что в данной задаче наиболее эффективными оказались корреляционные характеристики.

Таблица 1. Результаты дисперсионного анализа

№	Признак	J ( k )	е
1	Ближняя побочнодиагональная корреляция	3,71	0,32
2	Ближняя горизонтальная корреляция	3,60	0,52
3	Ближняя вертикальная корреляция	2,82	0,48
4	Дальняя побочнодиагональная корреляция	2,79	0,32
5	Ближняя главнодиагональная корреляция	2,50	0,56
6	Дальняя вертикальная корреляция	2,32	0,52
7	Дальняя горизонтальная корреляция	2,31	0,52
8	Ближний горизонтальный контраст Харалика	2,02	0,56
9	Дальний побочнодиагональный контраст Харалика	1,98	0,68
10	Дальняя побочнодиагональная разностная дисперсия	1,96	0,76

Рассмотрим контрольную выборку U е К K ^{х х} объёма V . Настроенный с помощью обучающей выборки U классификатор реализует отображение Ф ( v ), которое каждому вектору признаков U j ставит в соответствие класс, к которому его относит классификатор. Кроме того, относительно каждого вектора U j известен его реальный класс Ф ( U j ).

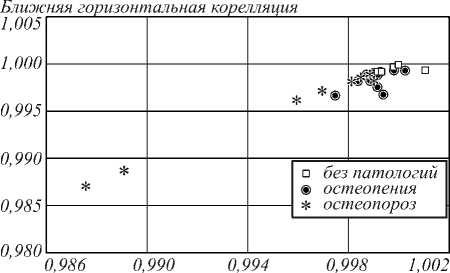
На рис. 3 наглядно показан разброс векторов из контрольной выборки в пространстве из двух лучших признаков, отобранных на основании дисперсионного анализа векторов из обучающей выборки.

Классификацию векторов будем производить с использованием правила ближайшего соседа. Этот алгоритм классификации выбран ввиду простоты реализации, высокой скорости работы, возможности обучения с учителем и низкой ошибки классификации [17].

Ближняя побочнодиагональная корелляция

Рис. 3. Векторы из контрольной выборки в пространстве из двух лучших признаков

Учитывая, что априорные вероятности появления объектов из различных классов неизвестны, имеем несмещённую оценку вероятности ошибочной классификации [17]:

£ = V |{ j е { 1,2, _ , Г} | Ф ( й? ) ^Ф ( Ц 7 _у )}|. (8)

В табл. 1 приведены значения такой ошибки с использованием каждого признака по отдельности. Видно, что ни один из них самостоятельно не справляется с задачей классификации.

Для отбора лучшей группы признаков воспользуемся аналогом процедуры, описанной в [16]. Однако в отличие от [16] будем добавлять в текущую группу очередной признак в порядке убывания критерия (7) и оценивать ошибку классификации (8) векторов из контрольной выборки, произведённой с помощью данной группы.

Таблица 2. Результаты отбора группы признаков

Группа признаков	£
1	0,32
1, 2	0,32
1, 2, 3	0,44
1, 2, 3, 4	0,36
1, 2, 3, 4, 5	0,40
1, 2, 3, 4, 5, 6	0,36
1, 2, 3, 4, 5, 6, 7	0,28
1, 2, 3, 4, 5, 6, 7, 8	0,20
1, 2, 3, 4, 5, 6, 7, 8, 9	0,24
1, 2, 3, 4, 5, 6, 7, 8, 9, 10	0,28

В табл. 2 представлены оценки вероятностей ошибочной классификации (8) для указанных групп признаков, номера которых соответствуют табл. 1. Видно, что первый локальный минимум наблюдается для группы из восьми признаков, из которых семь корреляционных и один признак Харалика. Оценка вероятности ошибки составляет 0,2.

На самом деле при классификации по группе из тридцати лучших признаков оценка вероятности ошибки составила 0,16, что меньше, чем 0,2. Но, во-первых, тридцать признаков – это уже достаточно много, и их вычисление занимает время (несколько секунд), а, во-вторых, учитывая небольшое число векторов в контрольной выборке, нельзя быть уверенным, что такая ошибка не была получена случайно.

Заключение

В данной работе был предложен способ автоматизированной диагностики остеопоротических отклонений по рентгеновским снимкам шейки бедра. На основании экспериментальных исследований эта методика была опробована, и было показано, что лучшими в данной задаче являются корреляционные характеристики изображения.

Предложенный метод диагностики обладает по сравнению с другими такими достоинствами, как низкая стоимость, высокая скорость постановки диагноза, распространённость необходимой аппаратуры, универсальность, учёт трабекулярной структуры костной ткани.

Тем не менее этот подход обладает и недостатками, такими как зависимость многих признаков от изменений общей яркости изображения, зависимость от выбора специалистом полигональной области интереса, невозможность учитывать возраст, пол и другие особенности пациента, которые учитывает денситометрия.

Высокая ошибка классификации связана, кроме собственно погрешности метода, прежде всего с фактом использования результатов денситометрии в качестве априорных диагнозов. Ведь результаты денситометрии основаны на минеральной плотности костной ткани, в то время как текстурные признаки характеризуют целостность трабекулярной структуры. Качество классификации предположительно можно повысить, если при обучении опираться на экспертную оценку снимков или на факты уже случившихся переломов.

В целом, результаты исследований показывают, что предложенный метод может быть использован в клинической практике для диагностики остеопороза при отсутствии аппаратуры для денситометрии или даже в дополнение к ней.