Исследование теплообмена в контактном аппарате с пленочными форсунками

В ряде тепломассообменных аппаратов энергетики и химической технологии происходит непосредственное взаимодействие газа и сплошной жидкостной пленки, вытекающей из кольцевой щели. В реактивном пространстве таких аппаратов газ взаимодействует со сплошной жидкостной пленкой, каплями, на которые распадается струя, и пленкой жидкости, стекающей по стенкам камеры. Существующие методики расчета подобных аппаратов оперируют параметрами, относящимися в целом к контактной камере, не выделяя из общего процесса тепломассообмена вклад каждой из зон. Анализ многочисленных опытных данных, полученных на промышленных и лабораторных установках [1, 2], позволил авторам создать упрощенную математическую модель процесса теплообмена в малоисследованной зоне - в свободной жидкостной пленке.

Рассмотрим установившееся течение осесимметричной жидкостной пленки, вытекающей из кольцевой щели (рис. 1). При взаимодействии жидкостной пленки с газовым потоком в полости тепломассообменного аппарата силы тяжести и поверхностного натяжения, действующие на элемент жидкости и стремящиеся свернуть пленку, компенсируются динамическим напором газа.

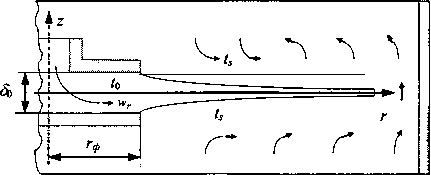
Рис. 1. Схема течения жидкостной пленки

В результате такого взаимодействия форма пленки становится близкой к форме диска, что характерно для многих тепломассообменных аппаратов. Неравномерный профиль скоростей на выходе из сопла достаточно быстро релаксирует к равномерному [3], и затем при взаимодействии с газом мало отличается от равномерного [4]. Длина участка релаксации может быть определена по уравнению / = C5Re[5], где значение коэффициента С принято равным 1/24, как и для случая истечения струи из бесконечной щели, поскольку поперечный размер пленки 8 г в реальных условиях меньше радиуса отбойного диска форсунки Гф на порядок и более. Для некоторых жидкостей, в частности для воды, длина участка релаксации со- ставляет 0,5-2,5 см, что значительно меньше радиуса разлета жидкостной пленки.

Задача значительно упрощается, если учесть отмеченные выше замечания и пренебречь влиянием пульсаций, обусловленных взаимодействием сил тяжести, инерции, поверхностного натяжения и вязкости. Результаты решения такой задачи могут быть распространены от устья форсунки до места распада струи на капли.

При постановке краевой задачи сделаны следующие предположения: процесс стационарный, свободная жидкостная пленка имеет форму диска, поле скоростей в жидкостной пленке практически равномерно, радиальная скорость и теплофизические параметры жидкости являются величинами постоянными, величина осевого градиента температур много больше радиального.

Запишем уравнение распространения тепла в жидкостной пленке в цилиндрических координатах, полагая, что осевой градиент температур много больше радиального градиента и радиальная скорость жидкости w_r значительно больше осевой скорости w_:

Начальные условия на выходе из сопла:

' = 'о-                 (2)

Граничные условия определим из условия, что на поверхности струи температура жидкости равна температуре насыщения:

2 = ^&_r t = t_s.              (3)

При заданных условиях теплообмена задача становится симметричной и начало координат удобно поместить на оси струи, как показано на рис. 1. Условие симметрии запишем в виде:

z=0, 5 = 0.                  (4)

Введем безразмерные координаты. Обозначим Л = г/?0, Z = z!br, & = (ts-t)/(ts-t0), где гф и г - радиус форсунки и текущий радиус струи; 8Г-поперечный размер струи на удалении г от сопла форсунки; t0, ts - начальная температура струи и температура насыщения. Экспериментальные исследования динамики свободной жидкостной пленки, представленные в [6], показывают, что скорость жидкости вдоль радиуса можно считать постоянной. Тогда из закона сохранения массы 2%pw080r^ = 2itpwr8rr выразим поперечный размер пленки б                                  (5)

r г R

С учетом последнего выражения и новых переменных RmZ уравнение (1) запишем в виде

89    ₂ Ьф 8²9 Z 89           _

----= ft------ /  \ cR Ре QZ2 R6Z

80wr где Ре =     - число Пекле, 0+= —— геомет-

«* 8

рическая характеристика форсунки. Начальное (2) и граничные (3) условия примут вид:

Я = 1, 9 = 1;(7)

Z = ±-, 9 = 0.(8)

Условие симметрии в безразмерных координатах примет вид:

Z = 0,   — = 0.(9)

8Z

Краевая задача (6)-(9) решена численными методами. Расчет средней температуры 9 в сечении R представлен на рис. 2. Задача решена для чисел Пекле и параметра Ь_ф характерных для режимов эксплуатации контактного теплообменника [1].

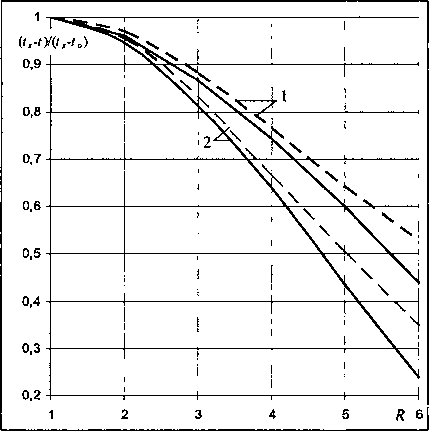
Рис. 2. Относительный прогрев жидкостной пленки: 1 - (£ф/Ре)=0,0005, 2 - 0,001; прерывистая линия -численный расчет, сплошная линия - расчет по формуле (12)

Предположим, что в уравнении (6) второе слагаемое в правой части с увеличением радиуса незначительно влияет на распределение температуры в пленке. Тогда уравнение теплообмена запишем в виде

89 _ ^2 ^Ф 8²9

8R Ре 8Z2 '

(Ю)

Краевую задачу (7)—(10) можно решить методом разделения переменных:

9 = ^k-^exp(-(3²(^ )PeV -1)) cos 0„Z, (11)

л=0 Vn где Р = (2и+1)л.

Уравнение (11) позволяет определить температуру жидкости в любой точке струи. На рис. 3

представлено распределение температуры в пленке на различном удалении от форсунки для характерного режима работы контактного теплообменника с пленочными форсунками. Для такого случая расчеты показывают, что верхний и нижний тепловые пограничные слои соединяются на расстоянии 7?=3,5.

Используя теорему о среднем определим среднюю температуру жидкости в сечении 7?

2            оо о

^= \MZ= ^^ехр(-р_и²(^/Ре)(Т?³-1)) . (12)

_1       л=0 Ри

Расчет средней температуры жидкости в сечении R , выполненный по формуле (12), представлен на рис. 2. Так как сплошность пленки воды сохраняется на расстояниях 7?=1 - 4,5...5,5 [6], то в этом диапазоне можно отметить хорошее соответствие численного и аналитического расчетов и справедливость принятого упрощения в отношении уравнения (6).

На рис. 4 представлены расчетные и опытные данные по теплообмену в жидкостной пленке. Опыты проведены на лабораторной установке [2], в которой свободная жидкостная пленка контактировала с продуктами сгорания дизельного топлива. За температуру t_s взята температура мокрого термометра входящих газов, являющейся предельной температурой нагрева воды в контактных аппаратах. В расчетное уравнение (12) заложены исходные параметры, создаваемые в экспериментальной установке, но при этом обнаружилось расхождение расчетных и опытных данных - в среднем на 38 % (рис. 4). Объяснение такого расхождения может быть следующее.

В опытах газ поступает в контактную камеру снизу и основной нагрев струи происходит через нижнюю поверхность, затем газ огибает жидкост ную пленку у стенки контактной камеры и далее на некотором расстоянии основной поток газа сосредотачивается у стенки контактной камеры. Над пленкой образуется застойная зона с небольшой циркуляцией уже частично охлажденного газа. В этой зоне интенсивность теплообмена низка и не обеспечивается прогрев поверхностного слоя пленки до температуры насыщения входящих газов. Таким образом, условие (8) на верхней поверхности пленки в опытах не выполнялось.

Для учета этого фактора сформулируем новую краевую задачу, в которой будем считать верхнюю поверхность жидкостной пленки теплоизолированной. Для удобства решения ось OZ свяжем с нижней поверхностью жидкостной пленки. Значения Z будут меняться от 0 до 1. В краевой задаче (7)—(10) уравнение теплопроводности (10) и начальное условие (7) остаются без изменений, условие симметрии (9) не соблюдается, а граничные условия (8) примут вид:

при Z = 0 9 = 0,                (13)

при 7 = 1 — = 0.               (14)

Решение краевой задачи (10), (7), (13), (14) также проведем методом разделения переменных. Ее решение имеет вид:

S^ е^Н^/РеДТ?3-1)) sin^Z, (15) ^₽n-smP„cos₽„ где Р„ = ^и+^л .

На рис. 5 представлено распределение температуры в жидкостной пленке на различном удалении от форсунки, рассчитанное по уравнению (15) при значении (ZyPe)=0,0021.

Средняя температура жидкости в сечении R

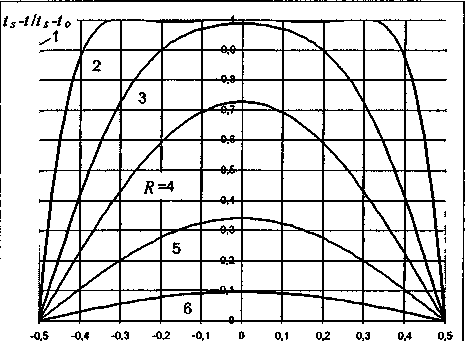
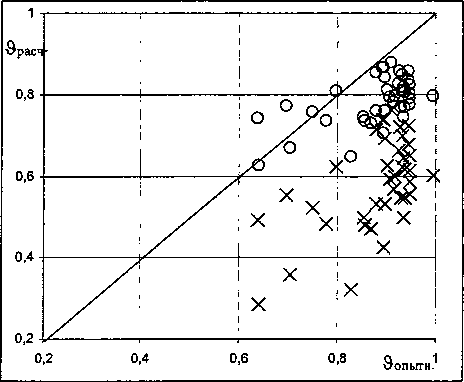
Рис. 3. Распределение температуры в жидкостной    Рис. 4. Соотношение опытных и теоретических данных по теплообмену в жидкостной пленке: х - расчет по уравнению (12), о - расчет по уравнению (16)

пленке: нагрев с двух сторон, (7^ Ре) =0,0021

_ 1 э = Jmz = о

-Ё _в в^м^в л ^^!^ -1». (16) №=oP«VP_n 8Шр_и COSp_n)

На рис. 4 сопоставлены опытные данные по теплообмену в свободной жидкостной пленке и расчетные данные по уравнению (16). Расхождение составляет в среднем 9,3 %.

Полученные выше уравнения позволяют приближенно решать задачу тепломассообмена в контактном аппарате с пространственными жидкостными пленками. Более точные данные, на наш взгляд, можно получить численным экспериментом, рассматривая сопряженную задачу тепломассообмена между газом и свободной жидкостной пленкой. В то же время уравнения (11), (12), (15) и (16) могут служить основой в постановке и отладке такого численного эксперимента.

Рассмотрим возможности упрощения расчета уравнений (11), (12), (15) и (16). Анализ сходимости ряда выполнен с помощью программы обработки электронных таблиц Excel, установленной в компьютере типа IBM. В [7] приведено классическое решение задачи теплообмена в плоской неограниченной пластине. Приведенный в [7] ряд при числе Фурье >0,3 становится настолько бы-стросходящимся, что распределение температуры достаточно точно можно описать первым членом ряда. Аналогичная зависимость выполняется для рядов, приведенных выше, но только в отношении комплекса Ьф/Ре. Кроме того, исследования показали, что ряд при фиксированном значении Ьф/Ре существенно сходится с удалением от сопла. Это объясняется тем, что безразмерный ра диус пленки R имеет показатель степени 3. Очевидно, что для уравнений (И), (12), (15) и (16) вопрос об ограничении ряда в практических расчетах необходимо решать по показателю {Ьф!Рё){^ -1), который при значениях < 0,3 может обеспечить достаточную точность вычислений (рис. 6). Обозначив в уравнениях (11), (12), (15) и (16) коэффициенты ряда в виде а - ЕЛ ехр(-^аф/РеХР3 -1)) cos (sin)P„Z , и=0

приведем их значения:

Коэф-ты уравнения	Р„ (Н),(12)	А„ (И)	А„ (12)	А (15),(16)	А„ (15)	А„ (16)
п=0	3,141593	1,27324	0,810569	1,570796	1,27324	0,810569
п=1	9,424778	-0,42441	0,090063	4,712389	0,424413	0,090063
п=2	15,70796	0,254648	0,032423	7,853982	0,254648	0,032423
п=3	21,99115	-0,18189	0,016542	10,99557	0,181891	0,016542
п=4	28,27433	0,141471	0,010007	14,13717	0,141471	0,010007
п=5	34,55752	-0,11575	0,006699	17,27876	0,115749	0,006699

Выводы

Сформулирована математическая модель теплообмена в сплошной жидкостной пленке и получено аналитическое решение в виде быстро сходящегося ряда.

• 1.    Проведено сравнение экспериментальных данных с аналитическими решениями для двух вариантов граничных условий.

• 2.    Показано, что для принятой схемы движения теплоносителей можно пренебречь теплообменом в кормовой зоне сплошной жидкостной пленки, обтекаемой поперечным потоком газа.

  

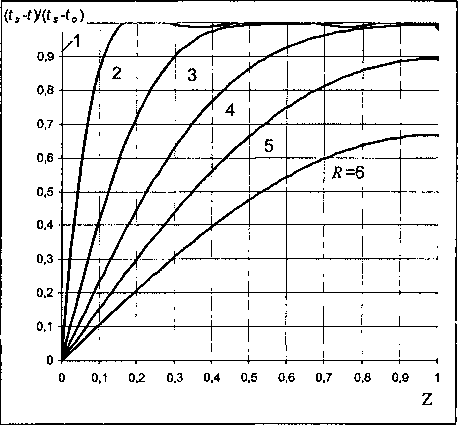
  Рис. 5. Распределение температуры в жидкостной пленке: нагрев с одной стороны, ^Ь_ф]Ре) =0,0021

  
  
  

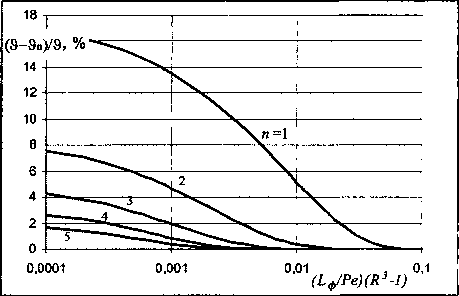
  Рис. 6. Относительная погрешность в определении средней температуры жидкостной пленки по п членам ряда уравнения (16)