Исследование теплового эффекта на основе наночастиц жидких кристаллов

Рахматуллина Р.Г., Нжийа Н., Русинов А.А., Маскова А.Р. Исследование теплового эффекта на основе наночастиц жидких кристаллов // Нанотехнологии в строительстве. 2024. Т. 16, № 3. С. 235–242. – EDN: HCIGHR.

Наноструктурные и высокодисперсные системы обладают химическими, электрическими, магнитными, механическими, оптическими и другими свойствами. Образование наностуктурных систем может привести к изменению физических свойств, а именно изменить предел прочности, текучести, теплоемкость, температуру, магнитные переходы и т.д., поэтому, обладая уникальными свойствами, широко привлекают внимание специалистов в области физики, химии, материаловедения, биологии [1–3].

В настоящее время известно, что течение жидкостей и газов по водопроводным, нефтепроводным и газопроводным трубам встречается во многих областях промышленности. Физико-химические законы течения жидкостей и газов оказывают важную роль на протекание процесса разделения.

В непрозрачных проводниках появляется задача определения направления, измерения величины потока жидкости и расхода потока объема жидкости в проводниках. Имеется несколько способов определения теплового эффекта и температуры [4–8]. В данной работе измерение теплового эффекта проводилось пирометрическим способом.

Рассмотрим два тела, приведем их в соприкосновение и будем нагревать.

Мы знаем, что при этом температура будет изменяться во времени. Соприкосновение тел приводит к увеличению движения мельчайших частиц, и, соответственно, будет происходить обмен энергией между мельчайшими частицами. Обмен энергией, передаваемой между мельчайшими частицами от более горячего тела к более холодному, называют тепловым эффектом (потоком). Таким образом, теплота распространяется от точки с более высокой температурой к точке с более низкой температурой во всех направлениях. Для возникновения теплового эффекта в различных поверхностях пространства достаточно в этих поверхностях создать разные температуры с наличием разности температур [9–13].

Тепловые трубы – важнейшие элементы теплоэнергетических установок, представляющие собой автономные, герметично-замкнутые, двухфазные теплопередающие устройства. Перечислим преимущественные достоинства: простота конструкции, способность выдерживать большие тепловые потоки при незначительных перепадах температуры, небольшая масса, тепловая труба может работать в широком интервале температур, к тому же теплопроводящие свойства тепловых труб выше, чем у самых теплопроводных металлов [14–19].

Принцип действия тепловых труб заключается в том, что перенос тепла происходит за счет того, что в горячем участке трубы жидкость испаряется, по- том конденсируется на холодном участке. Жидкость возвращается в испаритель за счет капиллярных сил [18–23].

При создании тепловых труб возникают трудно решаемые проблемы – это совместимость материалов.

Исследование и ремонт трубопроводов с использованием композитных материалов доказывает свою высокую эффективность [24–28].

МЕТОДЫ И МАТЕРИАЛЫ

Во всех телах перенос теплоты зависит от перераспределения температуры. Для появления перераспределения теплоты необходима разность температур.

Для изучения теплового эффекта собрана экспериментальная установка, которая состоит из термостата, нагревателя и термопары. Вода в термостате при постоянной температуре пропускается через проводник. Для нагревания участка внешней поверхности потока проводника используется нагреватель с пластиной. Температура в области нагрева определяется термопарой, показания которой выводятся на мультиметры [29–31].

В эксперименте в зоне проводника действует тепловой поток. Отметим, что на перераспределение теплового поля влияют такие процессы, как теплопроводность и теплоотдача. При теплопроводности перенос теплоты происходит на молекулярном уровне между различными частями тел. При броуновском движении молекул, атомов или наночастиц, при столкновении друг с другом происходит перенос энергии соответственно между молекулами, атомами или наночастицами. Когда по проводнику течет ток, выделяется мощность, при этом плотность тока также увеличивается, и все это приводит к увеличению выделения теплоты и температуры.

Для использования перераспределения теплоты в проводниках в расчетах нами предложено выражение закона Фурье:

q = – βT, где β – коэффициент теплопроводности; T – температура.

В результате неравномерного нагревания проводника наблюдаются тепловые потоки. Перераспределение температурного поля является довольно сложной задачей. Ранее проведенные экспериментальные исследования показали, что измерение температуры возможно только пирометрическим методом. Согласно пирометрическому методу, исследуемый образец должен покрываться тонким слоем материала.

Для наблюдения теплового эффекта использовались соединения на основе наночастиц жидких кри-

ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ

Таблица 1

Наименование соединений на основе наночастиц жидких кристаллов

№ Соединения жидких кристаллов Количественные соотношения соединений I Холестерилолеат и гексилоксибензойная кислота 6:2 II Холестерилолеат и нонилоксибензойная кислота 3:1 III Холестерилолеат и бутилоксибензойная кислота 5:2 сталлов. Жидкие кристаллы обладают уникальным свойством, таким, как текучесть, которая присуща обычным жидкостям.

На основании электронных спектров были рассчитаны размеры наночастиц жидких кристаллов в пределах от 1,7 до 4 нм. Сами соединения представлены в табл. 1.

Из табл. 1 видно, что для получения соединений жидких кристаллов во всех соотношениях применялся холестерилолеат, в основу которого добавлялись различные кислоты в разных количественных соотношениях. В данной работе использовалось соединение на основе наночастиц жидких кристаллов под номером I.

Для получения экспериментальных соединений использовалась следующая схема. В начале все соединения в представленных в табл. 1 соотношениях помещались в стеклянный сосуд. В первом случае частицы перемешивались специальной стеклянной палочкой, и соединения доводились до однородной массы. Второй случай позволил получить однородное распределение наночастиц. В третьем случае приготовленные соединения нагревались до температуры до полного расплавления.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Полученные соединения наносились тонкой пленкой на поверхность проводника (приблизительно 10 мкм). Далее на поверхности проводника осуществлялась теплоотдача с образованием многокрасочных цветов. Измерения проводились при помощи оптического пирометра, за начало отчета взята область нагрева.

На месте, где осуществляется нагрев, происходит поглощение тепла. При этом тепловое поле устремляется ровно и постепенно. Напомним, что на распределение тепла влияют теплопроводность и теплоотдача.

Нами были измерены зависимости изменения температуры на поверхности проводника с соединениями на основе наночастиц жидких кристаллов. В результате эксперимента получили три зависимости изменения температуры на поверхности проводника в зоне нагревания и в зоне охлаждения.

На рис. 1 приведен график зависимости изменения температуры в зоне теплового эффекта проводника в отсутствии движения жидкости.

На рис. 2 представлен график зависимости перераспределения температуры в зоне теплового

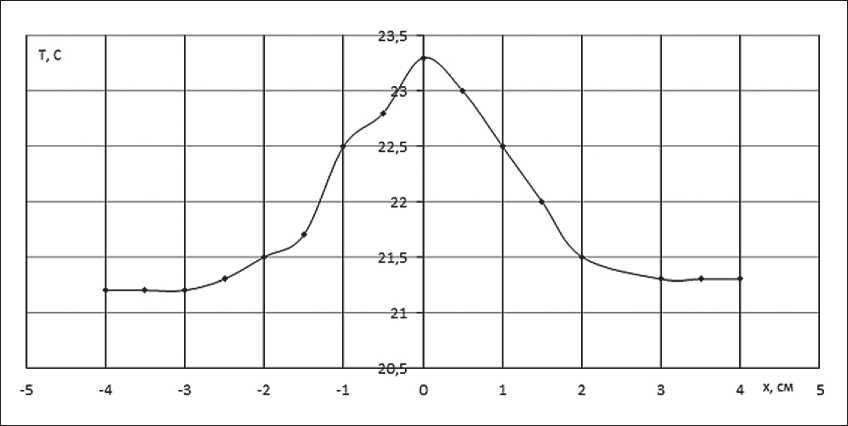
Рис. 1. График зависимости изменения температуры в зоне теплового эффекта проводника в отсутствии движения жидкости

ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ

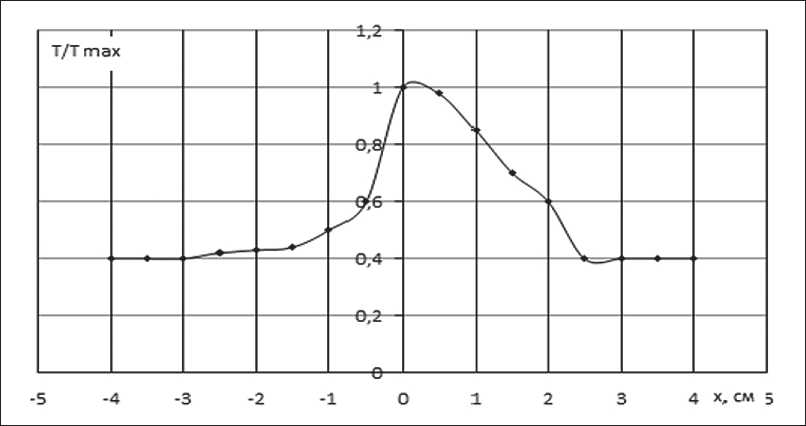
Рис. 2. График зависимости изменения температуры в зоне теплового потока проводника в присутствии движения жидкости

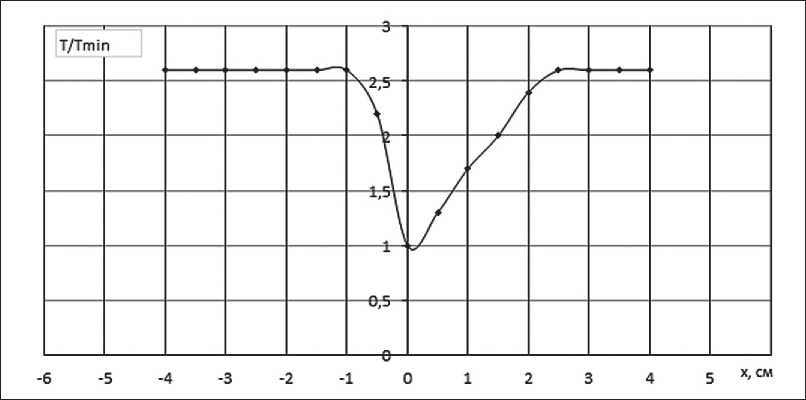
Рис. 3. График зависимости изменения температуры проводника в зоне охлаждения

эффекта проводника, когда присутствует движение жидкости.

Представленные на рис. 1 и 2 графики имеют нелинейные зависимости, и на всех кривых имеется четко выраженный максимум, который в зоне теплового эффекта в присутствии движения жидкости смещается [32, 33].

Из рис. 3 видно, что на месте, где осуществляется охлаждение потока проводника, график зависимости перераспределения температуры имеет ассиметрич-ные изменения.

Таким образом, из проведенных экспериментальных исследований получили наличие теплового эффекта жидкости [34]. В результате отметим, что при наличии движения жидкости и в отсутствии движения жидкости наблюдается неравномерное распределение температурного поля.

Скорость движения жидкости рассчитали по следующей формуле:

υ = Q / S ,                                       (1)

где Q – расход потока объема жидкости, м³/с ;

S – площадь поперечного сечения проводника, м2. Расход теплового потока рассчитали по фор муле:

Q = V / t ,                                          (2)

где V – объем жидкости, м³; t – время, с.

ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ

Таблица 2

Характеристики скорости движения и расхода потока объема жидкости

Скорость движения жидкости, υ , м/с	Расход потока объема жидкости, Q ·10–5 , м2/с
0,0995	1,66
0,0331	5,00
1,6600	0,83

Для наблюдения направления теплового эффекта математически рассчитали по вышепоказанным формулам величины скорости движения жидкости υ и расход потока объема жидкости Q [35] . Полученные значения представлены в следующей табл. 2.

Используя табл. 2, построили спектры (рис. 4) перераспределения температур на поверхности проводника для различных скоростей движения жидкости. Первому спектру соответствует скорость υ ₁ = 0,0995 м/с, второму спектру соответствует скорость υ ₂= 0,0331м/с и третьему спектру – υ ₃=1,660 м/с.

Из рис. 4 видно, что с повышением значений скоростей движения жидкости спектры перераспределения температур и тепловой эффект сужается.

В следующем графике приведена зависимость мощности нагревателя на поверхности проводника от скорости потока жидкости (рис. 5).

Как видно из рис. 5, для поддержания постоянной температуры с увеличением скорости надо увеличивать мощность нагревателя. До скорости 0,155 м/с наблюдается линейная зависимость, при дальнейшем увеличении значений скорости потока график становится более пологим. Возможно, в этой точке изменяется режим движения жидкости.

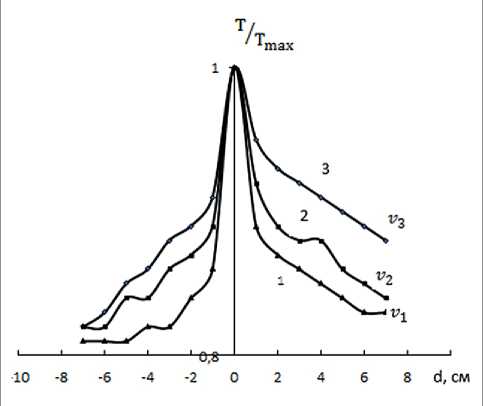
Рис. 4. Спектры перераспределения температур на поверхности проводника для различных скоростей движения жидкости

Анализируя полученные зависимости, можно математически вычислить величину потока жидкости [36].

Рассмотрим жидкость с температурой T , которая движется в проводнике с поперечной поверхностью S . Изменение температуры жидкости вдоль проводника равно:

dT = (t,x) = —dt + —dx ,

• 4        dtdx

dT  dTdTdx

T=VH .

dx   dtdx dt

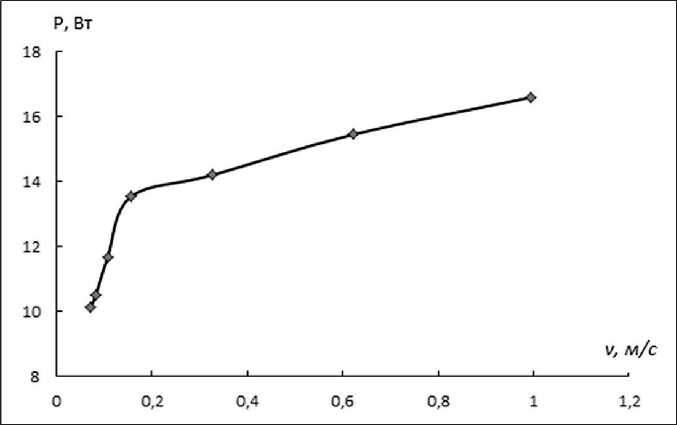
Рис. 5. График зависимости мощности нагревателя на поверхности проводника от скорости потока жидкости

ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ

Так как dx / dt = υ , тогда dT / dt = ( ∂T / ∂t + ∂T / ∂x ) υ , где ∂T / ∂t – производная температуры по искушению; ( ∂T / ∂x ) υ – конвективный член, характеризующий конвективные теплообменники.

Если температура остается постоянной во времени, то ∂T / ∂t = 0 , тогда получим выражение:

ат _ i dT dx v dt

Согласно уравнению (3), чем больше жидкость находится в движении (увеличение скорости), тем меньше происходит теплообмен с внешней средой, как показано на рис. 5. Зависимость мощности нагревателя для поддержания постоянной температуры на поверхности потокопроводника от скорости потока жидкости вначале характеризуется очень быстрым ростом мощности, а далее имеет линейную эволюцию (уменьшение мощности). Возможно, это связано с тем, что чем больше жидкость находится в движении, тем больше происходит обмен тепла путем конвекции.

При теплоотдаче на поверхности проводника появляются многокрасочные цвета.

На рис. 6 показано изображение, когда нет движения жидкости по проводнику.

Если в проводнике происходит движение жидкости, то имеет место тепловой поток и изображение при этом меняется (рис. 7).

Из рис. 7 видно, что белому цвету подходит холодная зона, а синему цвету подходит теплая зона проводника.

Далее дополнительно в данной работе рассмотрены влияния вязкости жидких кристаллов от концентрации наночастиц. Для этого в рамках исследования были рассмотрены нематические жидкие кристаллы с добавлением наночастиц ( Ta–Si ) c различными концентрациями. Приведем структурную формулу нематического жидкого кристалла 4-нитробензилиден-4’-гептоксианилин: C₇H₁₅–O– C₆H₄–N = CH–C₆H₄–NO₂.

Изменяли концентрацию наночастиц от 0,25 до 3%. С помощью лазерного анализатора определили размеры наночастиц Ta–Si . Средний диаметр наночастиц Ta–Si получился около 8 нм. В табл. 3 приведены результаты измерений вязкости нематических жидких кристаллов от концентрации наночастиц Ta–Si .

Таблица 3

Результаты измерений вязкости нематических жидких кристаллов от концентрации наночастиц Ta–Si

Концентрация наночастиц Ta–Si , %	Вязкость, η, мПа·с
Жидкий кристалл
0,25	315,1
0,50	354,7
1,00	374,6
2,00	385,2
3,00	433,4

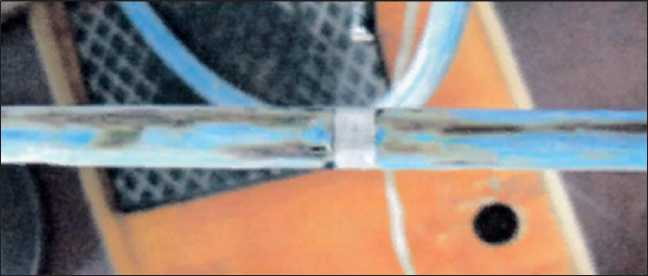
Рис. 6. Изображение теплового потока при отсутствии нагрева и движения жидкости

Рис. 7. Изображение теплового потока в наличии движения жидкости

ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ

Из приведенной выше табл. 3 видно, что с увеличением концентрации наночастиц Ta–Si вязкость жидких кристаллов увеличивается.

ВЫВОДЫ

При наблюдении теплового потока более эффективными оказались соединения на основе наночастиц жидких кристаллов, а именно хлестерилолеат и гексилоксибензойная кислота.

Приведенные выше данные показывают, что тепловой эффект на поверхности распределен неравно- мерно. Отметим, что вызванное локальное изменение температуры на поверхности проводника показывает несимметричность температурного поля. Это еще раз доказывает существование эффекта теплового потока.

В результате экспериментального исследования было показано локальное изменение температуры поверхности потока проводника.

Приведенный способ можно применить для эффективного определения направления потока в случае непрозрачных стенок проводника.

Соединение наночастиц приводит к изменению вязкости жидких кристаллов.