Исследование теплового состояния паропровода при пуске турбины Т-110 / 120-130 на базе обратной задачи теплопроводности

Технология пуска турбины в большой степени зависит от температурного состояния оборудования перед пуском. В соответствии с этим различают пуски из холодного, неостывшего и горячего состояния.

Пуск турбины из холодного состояния это пуск, когда температура металла низа ЦВД в зоне регулирующий ступени не превышает 200 0С. Пуском турбины из горячего состояния считается пуск, когда температура металла низа ЦВД в зоне регулирующей ступени более 400 0С. Существуют стационарные режимы, при которых параметры пара и тепловое состояние элементов конструкции турбоагрегата не меняются с течением времени, и нестационарные (переходные) режимы эксплуатации, связанные с изменением теплового состояния турбины при переходе из одного состояния в другое при изменении электрической или тепловой нагрузки.

К наиболее сложным случаям нестационарного режима относится пуск турбины, поскольку возникающие в процессе его термические и механические напряжения в элементах турбины – суммируется. Поэтому от правильного проведения пуска, останова существенно зависит эксплуатационная надежность и долговечность турбоагрегата.

В данной работе мы рассмотрели определение теплового состояния паропровода турбины на базе обратной задачи теплопроводности. Взяли экспериментальные данные при пуске турбины из холодного состояния, которые показаны в таблице 1. Данные записывались каждые 60 секунд.

Таблица 1 – Экспериментальные данные

01.10.2016 22:00:00	24,93
01.10.2016 22:01:00	24,94
01.10.2016 22:02:00	24,94
01.10.2016 22:03:00	24,96
01.10.2016 22:04:00	24,96
01.10.2016 22:05:00	24,99
01.10.2016 22:06:00	25,38
01.10.2016 22:07:00	27,77
01.10.2016 22:08:00	36,22
01.10.2016 22:09:00	47,48
01.10.2016 22:10:00	57,53
01.10.2016 22:11:00	66,04
01.10.2016 22:12:00	73,27
01.10.2016 22:13:00	79,4
01.10.2016 22:14:00	84,6
01.10.2016 22:15:00	89,02
01.10.2016 22:16:00	92,77
01.10.2016 22:17:00	96,03
01.10.2016 22:18:00	98,88
01.10.2016 22:19:00	101,44
01.10.2016 22:20:00	103,76
01.10.2016 22:21:00	105,9
01.10.2016 22:22:00	107,88
01.10.2016 22:23:00	109,77
01.10.2016 22:24:00	111,55
01.10.2016 22:25:00	113,29
01.10.2016 22:26:00	114,97
01.10.2016 22:27:00	116,6
01.10.2016 22:28:00	118,2
01.10.2016 22:29:00	119,77
01.10.2016 22:30:00	121,34
01.10.2016 22:31:00	122,89
01.10.2016 22:32:00	124,44
01.10.2016 22:33:00	125,94
01.10.2016 22:34:00	127,4
01.10.2016 22:35:00	128,85
01.10.2016 22:36:00	130,29
01.10.2016 22:37:00	131,67
01.10.2016 22:38:00	132,99
01.10.2016 22:39:00	134,25
01.10.2016 22:40:00	135,46
01.10.2016 22:41:00	136,61
01.10.2016 22:42:00	137,68
01.10.2016 22:43:00	138,69

01.10.2016 22:44:00	139,67
01.10.2016 22:45:00	140,56
01.10.2016 22:46:00	141,43
01.10.2016 22:47:00	142,25
01.10.2016 22:48:00	143,04
01.10.2016 22:49:00	143,75
01.10.2016 22:50:00	144,46
01.10.2016 22:51:00	145,09

Паропровод турбины решается как для пластины, эффективным методом является использования решения граничной обратной задачи теплопроводности (ОЗТ). Экспериментальные значения температур внутри паропровода необходимы для решения данной обратной задачи нестационарной теплопроводности (ОЗТ), в то время как для решения прямой задачи теплопроводности (ПЗТ) в объем предварительных сведений включаются теплофизические свойства материала тела (коэффициент теплопроводности, удельная теплоемкость и плотность), начальное распределение температуры и параметры граничных условий (температура или плотность теплового потока на ограничивающих поверхностях тела, коэффициент теплоотдачи и температура омывающей тело жидкости или газа). Для решения задачи будем рассматривать граничную обратную задачу нестационарной теплопроводности в постановке Коши.

Допущения при расчетах:

• 1)    Теплофизические свойства материала постоянны и не изменяются в

течение всего процесса нагрева.

• 2)    Принимая во внимание отношение наружного и внутреннего диаметров, расчет ведется как для неограниченной пластины.

• 3)    В расчете принимается, что наложена идеальная тепловая изоляция

  d T ( x, т ) d x

  
  

  = 0, т >  0

  x = 0

  
  

Таблица 2 –Обозначения

Обозначения
x –координата; τ–время; T ( x ,τ)–температура; a –коэффициент температуропроводности материала; λ–теплопроводность материала; с –теплоемкость; ρ–плотность;	Bi–критерий Био; Fo–критерий Фурье; α–коэффициент теплоотдачи; l 0 –полутолщина пластины; T f, 0 –температура   омывающей среды; T 0 –начальная температура.

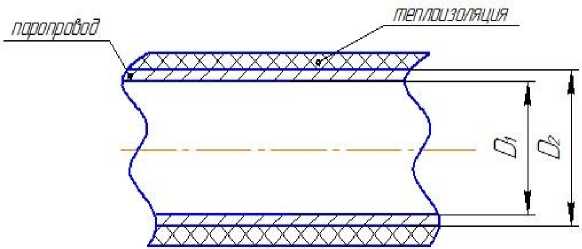
Рисунок 1 – Часть паропровода с теплоизоляцией

Аналитическое решение линейной одномерной обратной задачи теплопроводности на основе преобразования Лапласа

Рассмотрена граничная обратная задача в постановке Коши для неограниченной пластины, которая содержит уравнение процесса нестационарной теплопроводности [1].

d T ( x , t )       d ² T ( X , t )      _

------= a-- :—, т >  0

дт          d x ²

и установленные на одной из плоскостей (в точке х =0) зависимости от времени температуры

T (0, т ) = f ( т ), т >  0

и ее градиента

д T ( x , т)         , .      .

' ,      = Ф ( т ), т >  0

^д x    x = 0

На рисунке 2 в качестве примера показаны распределения экспериментально установленных функций f (τ) и φ(τ).

Применяя к задаче (1)–(3) интегральное преобразование Лапласа по

аргументу x

ГО

L (T ( x , t )) = V ( p , t ) = j T ( x , t ) • exp( - px ) dx , ⁰                                             (4)

при аппроксимации зависимостей f(t) и φ( t ) полиномами

nm f (t) = £ ak • tk            ф(t) = £bk • tk k=0                                   k=0

решение в оригиналах задачи (1)–(3) дает зависимость для искомого

распределения температуры

n

T(x, t) = X ak k=0

k + 1 t i = 1

k — i + 1      2 - i — 2

kVt • x

( k — i + 1)!(2 i — 2)!

m

+ X bk k=0

k + 1            k — i + 1     2 - i — 2

k vt • x

^X ( k — i + 1)! - (2 i — 1)!

и модуля её градиента:

д T ( x , t ) _ ^ k + 1 kVt^{k —} i ^{+ 1} • x^{2i — 3}

д x "t ! a k t24 k — i + 1)! - (2 i — 3)!

m

+ X bk k=0

k + 1            k — i + 1     2 - i — 2

kvt     • x

^X ( k — i + 1)! - (2 i — 2)!

(здесь под t понимается величина, равная a τ) .

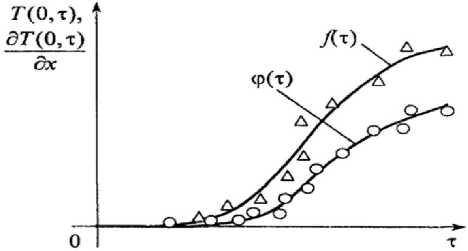
Рисунок 2 - Пример распределения температуры и ее градиента в пластине

Аналитическое решение ПЗТ

Для решения ПЗТ был написан алгоритм расчета в среде Mathcad 15.0 по формулам, представленным в работе. Исходные данные для расчета представлены в таблице 3, а его результаты на рисунке 3.

Таблица 3 – Исходные данные для расчета

Материал	Сталь марки 15Х1М1Ф
Температура пара, 0С	555
Коэффициент     теплопроводности, Вт/(мК)	33,44
Удельная теплоемкость,кДж/(кгК)	0,58
Плотность, кг/м3	7800

Использование аналитического решения ОЗТ

Исходными данными для расчета ОЗТ являлись приведенные на рисунке 3 результаты расчета ПЗТ. Аппроксимация решения ПЗТ производилась с помощью кубического сплайна, начиная с 13–ой секунды от начала нагревания пластины. Сравнение результатов решения ПЗТ и ОЗТ для точки х =0,018 м (в плоскости симметрии пластины) показало их практическое совпадение.

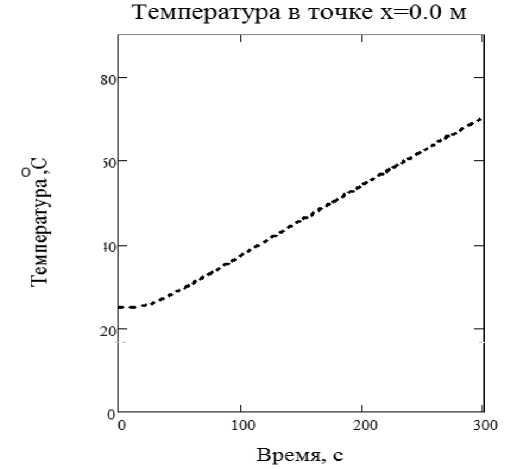
Рисунок 3 – Результат расчета ПЗТ для точки x =0 м

Для решения ОЗТ был написан алгоритм расчета в среде Mathcad 15.0. по формулам, представленным в работе. В работе производится аппроксимация экспериментальных данных. Вид аппроксимирующей кривой представлен на рисунке 4.

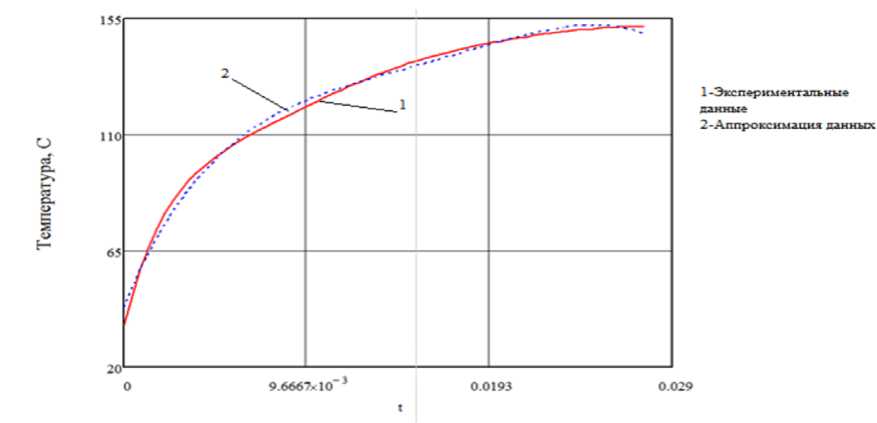
Рисунок 4 - Аппроксимация экспериментальных данных

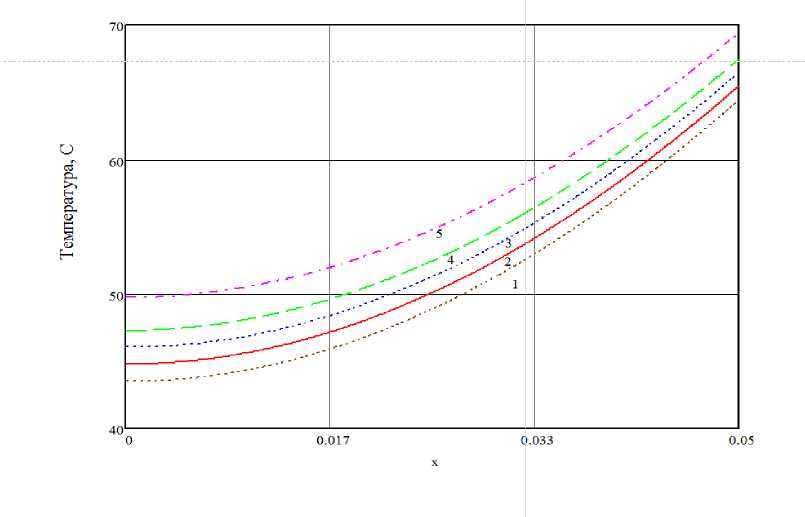
Рисунок 5 – Результат решения ОЗТ для паропровода

1–в начальный момент времени, 2–через 10 секунд после начала прогрева, 3–через 20 секунд после начала прогрева, 4–через 30 секунд после начала прогрева, 5–через 50 секунд после начала прогрева

Данные вычисления методом ОЗТ показывают как меняется температура прогрева паропровода турбины с внутренней стороны.