Исследование терморадиационной сушки технических тканей с использованием комплексных безразмерных критериев тепломассобмена

Сушка тканей термоизлучением является одним из эффективных способов термического обезвоживания материалов. За счет интенсификации процесса сушки и возникающих больших удельных тепловых потоков получают значительный технологический и экономический эффект [1]. Эффективность терморадиационной сушки заключается еще и в том, что оно обеспечивает высокотемпературный нагрев ткани, уменьшается миграция красителей и аппретов, при этом наблюдается высокая интенсивность испарения влаги с поверхности материала за счет максимальной глубины проникновения лучей в ткань и обеспечивается высокое качество обрабатываемого продукта [1]. Предварительно перед сушкой ткани проводят технологическую обработку специальными полимерными аппретами и клеевыми пропитками для обеспечения жесткости и каркасности. Нанесение аппретов на ткань с одновременным увлажнением производится в плюсовочных ваннах. Затем ткани подвергаются каландрированию для обеспечения равномерной влажности и поступают на сушку.

ПОСТАНОВКА ЗАДАЧИ

Сушка технических тканей производилась на металлической поверхности стола экспери- ментальной установки при вынужденном движении воздуха. Ткань располагалась параллельно от близко расположенных (250 мм) светлых источников излучения. В качестве излучателей использовались лампы с нихромовой спиралью со степенью черноты окисленного нихрома £1 = 0,82 v 0,90, стекла £2 = 0,82 ^ 0,92. При принятом расположении ткани от излучателей угловые коэффициенты излучения φ, характеризующие эффективность излучения φ = 1. Степень черноты натуральных тканей £ж = 0,75 ^ 0,80.

Исследование комбинированной конвективно-терморадиационной сушки тканей проводилось с трехкратной повторяемостью эксперимента для каждого режима с целью получения достоверных результатов. Сушка тканей проводилась при трех режимах: 1). 1_азл = 150 °С; t_c = 80 °С; 2). t_uM = 190 °С; t_c = 100 °С; 3). t^, = 250 °С; t_c = 120 °С. Скорость воздуха υ = 0,8 ÷ 1,1 м/с.

Решение системы уравнений тепломассо-переноса дает зависимость процесса сушки от большой группы тепломассообменных критериев подобия. Однако не все критерии в одинаковой мере влияют на характер протекания процесса сушки [2]. В условиях терморадиационной сушки тканей для безразмерной избыточной температуры можно записать

T* = f(X, Fo, Bi, Rb, Bo, £, Ko, Pd, Pn, W, Г), где T — относительная избыточная температура материала; X — безразмерная координата; Fo — критерий Фурье; Bi — критерий Био; Rb — критерий Ребиндера; Bo — критерий Больцмана; ε — критерий фазового превращения вещества; Ko — критерий Коссовича; Pd — критерий Предводителева; Pn — критерий Поснова; Ψ — коэффициент неравномерности распределения температуры и влажности в теле; Г — постоянная формы.

При изменении условий взаимодействия поверхности материала с внешней средой происходит изменение влияния критериев подобия на процесс сушки. В зависимости от роли и влияния на процесс сушки критерии подобия подразделяются на критерии поверхностного тепловлагообмена и критерии внутреннего теп-ломассопереноса [2]. Поскольку коэффициенты теплопереноса для тканей хорошо изучены [3], исследование сушки тканей тепловыми лучами ограничиваем изучением влияния критериев подобия на теплоперенос, а закономерности влагообмена рассмотрим на основе обработки экспериментальных данных. Зависимость коэффициентов теплопереноса для тканей приведены в таблице 1.

В процессе сушки тонких материалов

Таблица 1 – Зависимость коэффициентов переноса тепла от влажности тканей
Вискоза Х 0 = 0,058 Вт / м •Х; с 0 = 1600 Дж/ кг ^° С;					Лен Х0 = 0,058 Вт / м ^° С; с 0 = 1600 Дж/ кг ^° С;
W, %	^ 0 , Вт/ м ^° С	Р , кг / м3	с , Дж / кг -° С	а , м2 / ч	W, %	^ 0 , Вт/ м ^° С	Р , кг / м3	с , Дж / кг -° С	а , м2 / ч
90	0,187	759	2825	3,14	160	0,276	675	3150	4,67
80	0,173	713	2750	3,17	140	0,248	637	3060	4,58
60	0,144	640	2569	3,15	120	0,219	587	2960	4,537
50	0,13	600	2462	3,16	100	0,19	537	2840	4,49
40	0,116	556	2339	3,24	80	0,161	482	2690	4,48
20	0,087	488	2031	3,16	60	0,132	430	2500	4,47
10	0,072	453	1835	3,11	40	0,104	374	2260	4,41
					20	0,075	321	1946	4,32
					10	0,06	294	1744	4,27

при значениях теплообменного критерия Био Bi < 0,2 и критерия Фурье Fo > 0,2 происходит быстрое прогревание материала за счет глубокого проникновения излучения в ткань и выравнивания температур и влагосодержаний по поверхности и объему [1, 4]. В этих условиях сушка тканей происходит без температурных градиентов внутри тела и отсутствия в материале термического переноса вещества [2].

В отсутствии термического переноса вещества и фазовых превращений в тонких материалах влияние комплексного критерия е • Ko • Pn = 0 [2]. Критерий Ребиндера Rb и критерий Био Bi оказывают влияние на тепло-перенос. При малых значениях этих критериев влияние на скорость изменения температуры dT / dFo незначительно. В процессе сушки с уменьшением влагосодержания критерий Rb увеличивается, а критерий Ko уменьшается. Значения критерия Rb к концу сушки Rb = 0,1 ^ 0,35 указывают на необходимость прекращения процесса для избежания перерасхода энергии на сушку и пересушивания материала. Критерий Коссовича Ko на начальной стадии сушки большее влияние оказывает на массоперенос, в заключительной — на теп-лоперенос [2]. Скорость прогрева материала определяется комбинированным отношением критериев Bi / Ko = f(Fo) [2]. Критерий фазового превращения е и критерий Поснова Pn в отсутствии термического переноса вещества ε · Pn = 0 (влага в материале перемещается в виде жидкости). Постоянная формы тела для плоских тел Г = 0. Коэффициенты неравномерности распределения температуры W _t и влагосодержания ^ _ц во влажном теле при значениях критерия Bi < 0,2 для тканей равны W _t = W _u = 1. Происходит быстрое выравнивание температур и вла-госодержаний в теле по поверхности и объему. Произведение критериев Fo и Предводителева Pd представляют важные обобщенные переменные по температурам и влагосодержаниям

„ аттХ „

, (1)

I гх. * 11 К ' х ' а где a — коэффициент температуропроводности, м2/с; т — время сушки, мин; RV — отношение объема тела к поверхности, м; mt и m^ — темп нагревания влажного тела и темп убыли влаго-содержания, мин-1.

Радиационный критерий Больцмана Во получен из решения уравнения энергии для сложного теплообмена в плоском слое поглощающей и излучающей среды с непрозрачными серыми границами [5]. В результате решения получен безразмерный комплекс

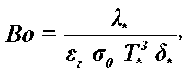
где Л , — теплопроводность излучающей непрозрачной среды; £ _г — степень черноты излучающего газа; а ₀ — константа излучения абсолютно черного тела, Вт/м² К⁴; T , — абсолютная температура излучающей среды по толщине излучающего слоя 6 * .

А.Н. Пехович [6] использовал критерий Во для расчета температуры твердых тел при нагреве и охлаждении по номограммам. Для случая радиационного теплообмена в прозрачной непоглощающей среде критерий Больцмана имеет вид:

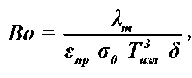
где Л _т — теплопроводность тела; е _пр — приведенная степень черноты системы излучатель-материал; Т_изё — абсолютная температура излучателя, К; δ — толщина материала, мм.

При построении расчетных графиков необходимы дополнительные условия: начальная температура материала Т_ож ; температура излучателя Т_изё ; отношение Т_ож / Т_изё , приведенная степень черноты системы излучатель–материал е _пр и безразмерная координата х / 6 .

Безразмерная избыточная температура Т* задается условием

,                      (4)

t£ "" С где tc , t, t0M — температура среды (воздуха), среднеинтегральная, и начальная температура влажного материала, °С.

За определяющую температуру при сушке тканей принималась температура теплоносителя (среды) tc. Степень черноты системы излуча- тель–материал определялась по зависимости

,

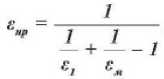
где £ 1 и е _ж — степени черноты нихромового излучателя и материала.

Критерий Во₀ абсолютно сухих тканей при заданных значениях £ _пр зависит только от режима сушки Т_мё , поскольку коэффициент теплопроводности сухих тканей Х ₀ от температуры не зависит [3]. Численные значения Bo w для влажных тканей значительно зависят от влажности. Влияние влажности тканей на теплопроводность и теплоемкость значительно и выражается зависимостями [3]

, Вт/м°С;

, Дж/кг°С,

№    1 + и где А0 и Aw — теплопроводности сухого и влажного материала, Вт/м°С; с0 и св - теплоемкости сухого тела и воды, Дж/кг°С; W и U — абсолютное и относительное текущее влагосодержание материала.

Плотность влажной ткани p w измерялась в эксперименте весовым способом. Коэффициент температуропроводности а влажной ткани вычислялся по соотношению

, м2/ч.

С» Pw

Значения коэффициентов теплопереноса для тканей даны в таблице 1.

Безразмерная координата X = х / 8 при х = 8 для тонких материалов X = 1. В качестве определяющего размера принимается отношение объема тела к поверхности R_V = V / F = 8 .Упро-щенное критериальное уравнение для безразмерной температуры можно представить в виде

T * = f( Fo , Pd_t , Rb , Bi / Ko , Bo ) , где Fo • Pd_t = m_t т .

РЕГУЛЯРНЫЙ ТЕПЛОВОЙ РЕЖИМ

В процессах нагревания или охлаждения твердых тел широко используется теория регу- лярного режима Г.М. Кондратьева, согласно которой процесс нагревания определяется только условиями внешнего теплообмена, теплофизическими свойствами и размерами тела, а температура материала изменяется во времени по экспоненциальному закону [4]. Нагрев влажного тела в процессе сушки при tc = const представляет регулярный режим, как по температурам, так и по влагосодержаниям [4], поскольку и кривые сушки и температурные кривые представляют собой экспоненты.

Основным признаком регулярного режима в процессе сушки являются условия

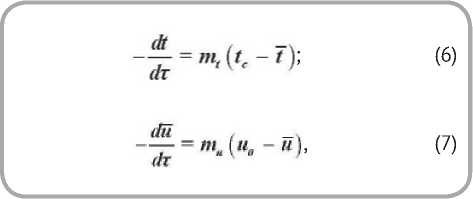
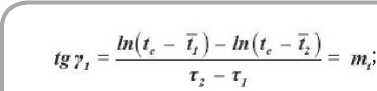
где и₀ — начальное влагосодержание материала.

Постоянные m_t и т_и определяются экспериментально, построением г р афических зависимостей ln(t_c -t) и ln(W₀ - W) от времени сушки т .

Темп нагревания влажного тела и темп убыли влагосодержания т_и находятся из соотношений

,      (9)

г, - г, ч________________________________7

где t_c — температура среды (воздуха), °C; t 1 и t₂ — фиксированные значения температуры, °C; W₀ — начальное влагосодержание материала; W 1 и W 2 — фиксированные значения влаго-содержания.

Из уравнения теплового баланса для стадии регулярного режима [4] можно записать выражение для темпа нагревания влажного тела

,

,

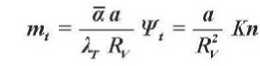
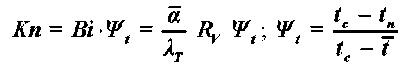
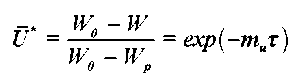
где а -текущее значение коэффициента теплообмена, Вт/м²°С; W t - коэффициент неравномерности распределения температуры в теле; Kn - критерий Кондратьева; t n - температура поверхности, °С.

При сушке тканей R V = 0,8 -1,2 мм и при значениях критерия Bi < 0,2 коэффициент формы К_ф ^ 0, а коэффициент неравномерности распределения температуры в теле W t = 1.

В этом случае Kn = Bi , а темп нагревания влажного тела равен [4,7]

где W 0 , W p , W p - начальное, равновесное и текущее влагосодержание материала.

Секундный поток тепла на нагрев влажного тела [7]

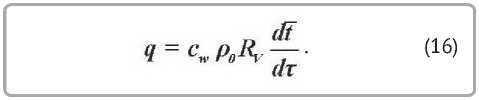
Дифференцируя решение (13) и подставляя результат в (16), получаем [7]:

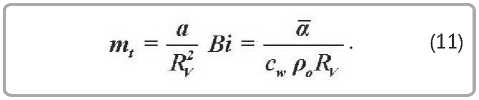
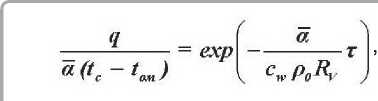
Для случая нагревания влажного тела при Bi ^ 0 и отсутствия градиента температуры внутри тела можно записать балансовое уравнение тепла [4,7]:

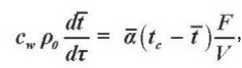
где F - площадь поверхности влажного тела, м²;

V - объем влажного тела, м³.

Тепло а (t c -1) идет на нагревание влажного тела. Решение (12) можно записать следующим образом [7]:

.

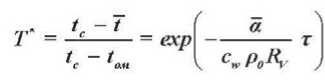
Из уравнений (11) и (13) следует

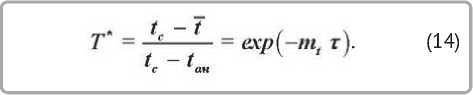
В результате обработки экспериментальных данных методом наименьших квадратов получено значение темпа нагревания для влажных тканей m_t = 0,24. Вычисление m_t по зависимости (11) дает значение m_t = 0,3 - 0,4.

Для безразмерного влагосодержания можно написать аналогичное соотношение:

где t c , t_0M - температура среды (воздуха) и начальная температура влажного материала, °С.

Максимальное количество тепла, затраченное на испарение влаги из материала в начальной стадии процесса сушки, равно:

q = а (t - t ) = r p R „ (du /d r )  . (18)

max кр ^v c ом      0 V          max ()

где (du /d r )_max = N_max - максимальная скорость сушки, определяемая по кривым сушки; r - теплота парообразования, Дж/кг.

Тогда уравнение (17) с учетом (18) можно записать в виде q = qmax exp(- mtT).          (19)

Следовательно, регуляризация кинетики сушки происходит не только по температурам и вла-госодержаниям, но и по тепловым потокам.

ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ И ВЫВОД ЭМПИРИЧЕСКИХ УРАВНЕНИЙ

На рисунке 1 представлены кривые сушки и температурные кривые в процессе сушки вискозной ткани при различных режимах. Видно, что периода постоянной скорости сушки не наблюдается ни по температурам, ни по влагосо-держаниям.

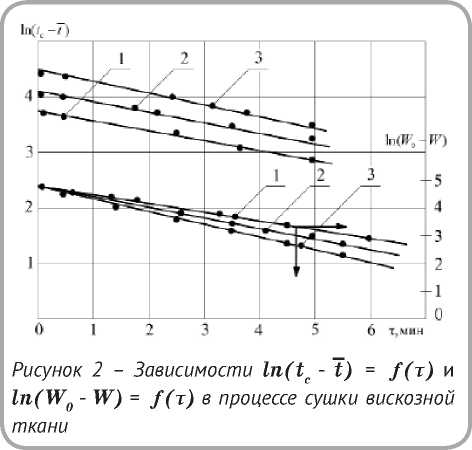
На рисунке 2 изображены графические зависимости ln(t c - t) = /( т ) и ln(W 0 - W) = /( т ) для процесса сушки вискозы. Видно,что зависимости имеют вид прямых и, следовательно, изменение температуры и влагосодержания происходит по экспоненциальной зависимости. Темп нагревания влажного тела m_t является одинаковым для всех точек тела и не зависит от режима сушки. В стадии регулярного режима при Bi < 0,2 и W _t = 1 температура принимает равномерное распределение по всему объёму тела и поверхности. Величина m_t не зависит от размеров, физических свойств тела, режима сушки и в стадии регулярного режима является величиной постоянной для среднеинтегральных значений температур и определяется только формой и видом тела [4,7].

Темп убыли влагосодержания т_и является сложной функцией режима сушки, начального влагосодержания материала W 0 , способа подвода тепла и других факторов, влияющих на сушку. Обработка опытных данных показала, что отношение максимальной скорости сушки тканей к начальному влагосодержанию W 0 является обобщенной переменной, учитывающей влияние всех факторов, воздействующих на процесс.

На рисунках 3 и 4 представлены результаты обработки экспериментальных данных в виде зависимостей U * = /(т_и т ) ; m_u = f(N_max) , T * = /(m i и T * = f(BO w ) .

В результате обработки данных методом наименьших квадратов получены уравнения

Т’ = ——-^— = ехр(-1,15т₁т^ ;     (20)

и - Н⁷

U* = —¹-----= 0.17 ехр( т г);     (21)

X/

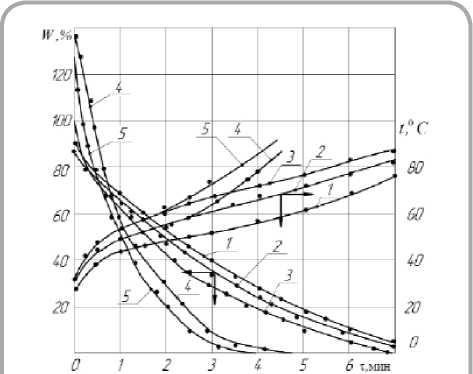
Рисунок 1 - Кривые сушки и температурные кривые в процессе сушки вискозной ткани при режимах: Вискоза. 1. t^ = 150 °C; t_c = 80 °C; 2. t „зё = 190 °C; t_c = 100 °C; 3. t_ = 250 °C; t_c = 120 °C; Лен: 4. t_um = 190 °C; t_e = 100 °C; 5. t_u3ё = 250 °C; t_c = 120 °C;. Скорость воздуха: и = 0,8 ^ 1,1 м/с.

значительно экономит время и сокращает объем

,

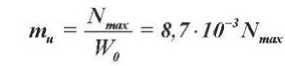
расчетной работы. Решение уравнений (20) и

(21) дает

где N_max = (du /di) — максимальная скорость сушки материала, мин^-1.

Использование устойчивых обобщенных комплексных переменных т ^ и т т позволяет определять температуру материала и время сушки при любых режимах и различных начальных влагосодержаниях. Такой метод исследования

—          t - t t - tr--£---и— r ехр(1Д5т,т)

.

г = — bi---- ------ т. 0,17 (W.-W,)

.

Для исследования влияния на кинетику сушки тканей критериев подобия необходимо знать закономерности их изменения. Вычисление коэффициента теплообмена проводилось по критериальному уравнению [1]

f т* X' / т¹ X* ^ / X^

,      (24)

где Nu — критерий Нуссельта; Re — критерий Рейнольдса; T_ì , T_èçë и T_ñ — абсолютные температуры мокрого термометра, излучателя, среды (воздуха).

За определяющий размер при сушке тканей принималась длина образца по набеганию потока воздуха l = 0,12 м.

Плотность теплового потока определялась по уравнению теплообмена q =«(te - tn).

Критерий Ребиндера Rb и критерий Коссови-ча К о вычислялись по соотношениям _.

с С (t-t ) w          н* ' с ан '

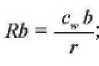
Температурный коэффициент сушки b = d t / d è — важнейшая характеристика кинетики сушки, определяется графическим диф ф еренцированием температурных кривых t = f(u) (рисунок 5 а ). Обработкой эксперимента, представленного на рисунок 5 б , получена зависимость

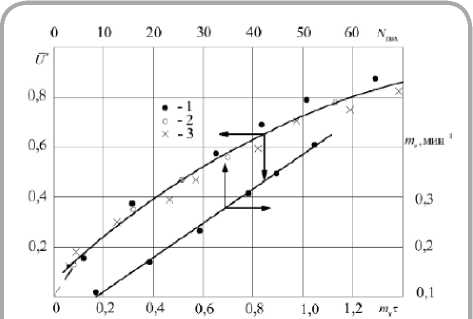
Рисунок 3 – Зав и симость относительного влагосодержания U^* от относительного времени сушки т_и т и зависимость темпа убыли влагосодержания m_u = /(N max ) для процесса сушки вискозной ткани при режимах, указанных на рисунке 1

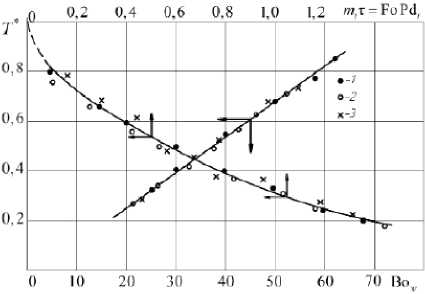
Рисунок 4 – Зависимости относительной

избыточной температуры T* = f (mtT) и T* = / (Bow) для процесса сушки вискозной

ткани. Режимы сушки даны на рисунке 1

Rb = 0,1 exp ( - 1,4 (и - u p )) .     (25)

представлены зависимости для процесса сушки вискозной ткани

В процессе сушки влажных материалов критерий Rb изменяется от нуля до некоторой максимальной величины, указывающей на прекращение процесса, а критерий К о — от максимальной величины в начальной стадии сушки до нуля при W = W_p .

Результаты исследования влияния критериев подобия теплообмена на закономерности изменения относительной температуры T^* для всех режимов даны в таблице 2, а на рисунке 6

Bi / Ko = f (Fo • Pdt) = f (mtT) и

T * = f (Fo • Pd t ) = f (m t T ) .

Зависимость относительной избыточной тем пературы T* = f (Bi I Ko) имеет вид

T* = 0,06 (Bi / Ko)0-5.          (26)

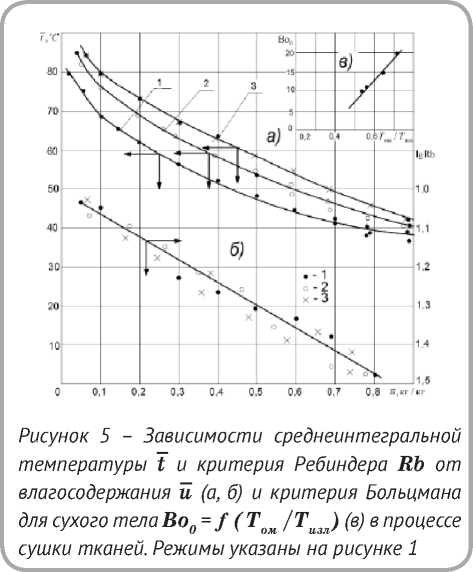
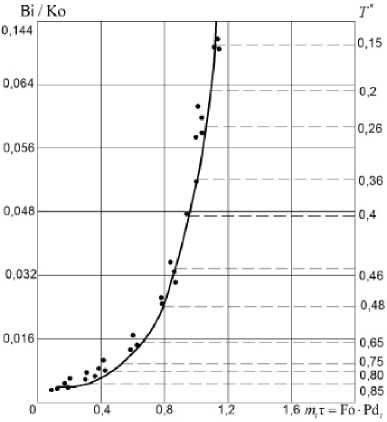
Рисунок 6 – Зависимости отношения критериев Bi/Ko и относительной температуры Т * от комбинированного критерия Fo • Pd_t = m_t T в процессе сушки технических тканей для заданных режимов сушки

Рассмотрим влияние критерия Больцмана на тепломассоперенос в процессе терморадиационной сушки тканей. При терморадиационной сушке влажных материалов значительно интенсифицируется теплообмен и увеличивается интенсивность испарения влаги с поверхности влажного тела. В этих условиях критерий Больцмана в одинаковой мере влияет на тепло- и вла-гообмен.

Численные величины критерия Bo₀ для сухих тканей при заданных режимах сушки в зависимости от режима при Л_о = const принимали следующие значения для вискозной и ткани:

• 1.    Т_азл = 423 K; t_c = 80 °С; Т_ож / Т_азл = 0,71; ВО о = 18.

• 2.    ^Т... = ⁴⁶³ К; t =¹⁰⁰ °С; ^То. / ^Т^ = ^0,65; Во₀ = 15.

• 3.    Т_изл = 523 К; t_c = 120 °С; Т_ож / Т_изл = 0,57;

ВО 0 =

На рисунке 4 представлена зависимость Т * = f (Bo w ) для процесса сушки вискозной ткани, описываемая уравнением

Т* = 0,0135 (Bo0 + 0,55 W),   (27)

Bo w = Во₀ + 0,55 W .           ⁽²⁸⁾

Критерий Больцмана Bo для сухого материала является функцией Т_изл и отношения

Т_ож / Т_и3ё и определяется зависимостью

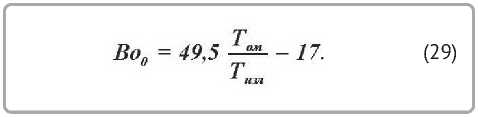
Взаимосвязь между критериями Больцмана для влажной и сухой тканей при сушке тепловыми лучами для заданных режимов можно выразить уравнениями

;            (30)

.        (31)

где W — заданное текущее влагосодержание материала.

Плотность тепловых потоков в процессе сушки тканей достаточно точно вычисляется по уравнениям (18) и (19). На рисунке 7 б даны за-

Таблица 2 - Расчетные значения критериев Нуссельта Nu , Био Bi , Коссовича К о для процесса сушки вискозной ткани при различных режимах

Режим сушки: Т_азё = 423 K; t_c = 80 °С; v = 1,1 м/с

W , %	Nu	а , Вт/м2°С	Bi	Ko	Bi / Ko	T*	t 3KC , °С	t pac , С
80	87,7	26,3	0,13	31,7	0,004	0,84	40	38
60	78	23,4	0,138	20	0,007	0,76	44	42
40	63,1	18,9	0,135	12,7	0,011	0,65	50	48
20	46,2	13,9	0,132	5,4	0,024	0,46	61	58
10	32,2	10,2	0,125	2,5	0,049	0,35	67	64
		Режим сушки: T èçë		= 463 K; tc =	100 °С; v =	1,1 м/с
80	94,9	30,5	0,145	29	0,005	0,84	45	42
60	83,6	26,8	0,151	17	0,0088	0,75	50	48
40	68,3	21,8	0,155	9,85	0,0157	0,65	56	55
20	50,1	16,2	0,157	4,7	0,033	0,48	68	69
10	26,5	11,7	0,145	2,2	0,066	0,38	73	73
		Режим сушки: T èçë		= 523 K; tc =	120°С; v =	1,1 м/с
80	104	34,4	0,168	29	0,0058	0,86	46	43
60	91,8	30,3	0,17	16	0,01	0,76	53	52
40	75	24,7	0,175	9,4	0,018	0,69	63	64
20	54,9	18,1	0,178	4,3	0,0410,	0,50	74	75
10	40,3	13,5	0,165	2,2	075	0,45	80	79

висимости q = f(W) , которые выражаются уравнением

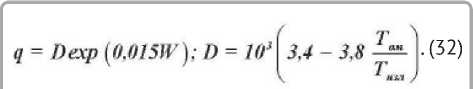
Для подтверждения достоверности полученных значений тепловых потоков по уравнениям (19) и (32) проведен расчет теплообмена по формуле излучения Стефана-Больцмана с учетом влияния конвекции [3]:

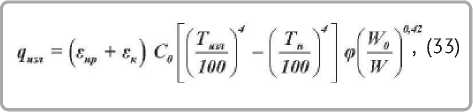
где Ñ₀ — коэффициент излучения абсолютно черного тела, Вт/м² К⁴.

Угловой коэффициент эффективности излучения ф = 1.

Приведенная степень черноты системы определялась по выражению (5).

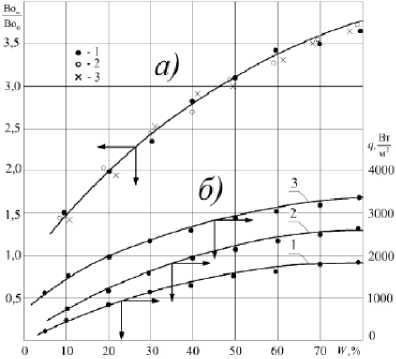
Рисунок 7 – Зависимости комбинированного отношения критерия Bo_w / Bo₀ и плотности теплового потока q от влагосодержания W для процесса сушки вискозной ткани при режимах,

указанных на рисунке 1

Участие конвекции учитывается увеличением степени черноты системы за счет е _к :

ВЕСТНИК ВИТЕБСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА

ВЫПУСК 27

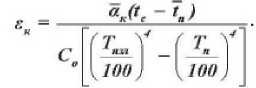
При использовании уравнения (33) суммарное значение ( е _пр + е _к ) составляло 0,66 - 0,7 для всего процесса сушки тканей. Результаты расчетов q_u3 ^ по формуле (33) даны в таблице 3.

ГРАФИЧЕСКИЙ РАСЧЕТ КИНЕТИКИ СУШКИ ТКАНЕЙ

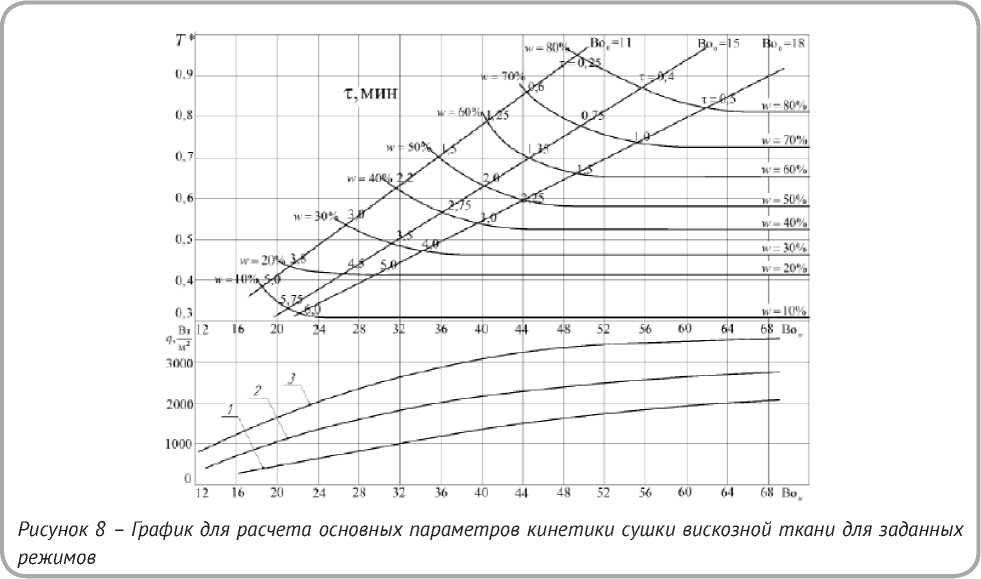
По результатам экспериментов (рисунке 1) вычисляются значения относительной избыточной температуры Т* как функция влагосодержа-ния Wтканей. Затем, с использованием таблицы 1, вычисляются значения критериев Больцмана для абсолютно сухой и влажной тканей. По эмпирическим формулам (27, 28) наносятся линии Во0 = const с фиксацией значений влагосодер-жаний для каждого режима сушки и строятся линии W = const с обозначением времени сушки т = f (W). В нижней части графика (рисунок 8) наносятся зависимости плотности тепловых потоков q = f (Bow, W). Таким образом, все основные характеристики сушки тканей тепловыми лучами рассчитываются графическим способом, что позволяет достаточно просто, точно и быстро проводить все необходимые расчеты, что экономит время и сокращает объем расчетной работы. График (рисунок 8) является расчетной номограммой.

Для расчетов по графику достаточно знать режим сушки, который задается значением Во₀ и текущим влагосодержанием W . В таблице 4 дано сопоставление экспериментальных и графических значений основных параметров кинетики сушки вискозной ткани по графику рисунка 8.

Пример расчета: Режим сушки вискозы Т_иё = 423 K, Т_ож / Т_цзл = 0,71. Для данного режима Во₀ = 18. По заданному текущему вла-госодержанию W = 60 %, относительная температура Т * = 0,66; интегральная температура ^ граф = ⁴⁴ °С; L = ⁴³ °С; время сушки: ^Т граф = ^{1,5 ми}н; ^Т » с = ^{1,5 ми}н; ^Bow граф = ^49,5; ^BOw раса = ⁵¹ Bo w _расч = 50,5 по формулам (28) и (31).

Для вискозной ткани расчетный график строится в том же порядке, с использованием тех же эмпирических уравнений.

ЗАКЛЮЧЕНИЕ

В процессе исследования терморадиационной сушки тканей рассмотрено влияние отдельных критериев подобия теплообмена на кинетику сушки технических тканей. Изучение кинетики

Таблица 3 – Сравнение экспериментальных и расчетных значений среднеинтегральных температур, времени сушки и плотностей тепловых потоков по формулам (22), (23) и (19), (32), (33) для различных режимов сушки вискозной ткани
Режим сушки: Тизё = 423 K; tc = 80 °С; v = 1,1 м/с
W , %	Т ЭК с , мин	Т рас , мин (23)	t ,KC , °С	t pac , С (22)	q , Вт/м2 (19)	q , Вт/м2 (32)	q3K c , Вт/м2	q .3^ , Вт/м2 (33)
80 60 40 20 10	0,65 1,95 2,85 4,5 5,4	0,72 1,76 3,2 4,3 4,9	42 54 61,5 71,5 78	40 54 62 72 78	2750 2314 1965 1380 1980	3060 2280 1795 1270 1020	2650 2270 2000 1280 850	2880 1890 1750 1100 780
Режим сушки: Тим = 523 K; tc = 120 °С; v = 1,1 м/с
80 60 40 20 10	0,4 1,25 2,32 3,7 5,7	0,47 1,45 2,54 3,35 5,2	42 55 68 77 83	39 54,5 68 79 85	3510 3140 2585 2140 1427	3900 3150 2350 1780 1495	3420 3125 2620 2000 1500	3300 2780 2100 1690 1250

сушки тканей методом регулярного теплового режима нагревания влажных тел и обработка опытных данных на основе обобщенных переменных позволяет получить расчетные эмпирические уравнения для определения основных кинетических характеристик процесса. Определены темп нагревания влажного тела mt и темп убыли влагосодержания т^. На основе взаимо- связи между критерием Больцмана для сухого и влажного тела предложен графический способ расчета кинетики сушки тканей, что экономит время и средства на проведение эксперимента и сокращает объем расчетной работы. Предлагаемый метод исследования может быть использован в расчетах кинетики сушки различных влажных материалов термоизлучением.

Таблица 4 – Сопоставление экспериментальных и графических значений основных параметров кинетики сушки вискозной ткани по графику рисунка 8
Режим сушки: Т				из „ = 423 K; t c = 80 °С; v = 1,1 м/с
W , %	Т экс ,с	Т рас , с (23)	т * экс	т * граф	t^c , °С	tг!>аф , С	Ч экс , ВТ/м 2	^ граф , Вт/м2 (32)
70	62	64	0,76	0,75	43	40	1850	1850
60	90	89	0,67	0,66	46	44	1700	1600
40	180	180	0,54	0,53	51	49,5	1250	1270
20	285	300	0,39	0,42	60,5	59	850	750
10	365	360	0,38	0,33	67	64	500	600
		Режим сушки: Тмё = 463 K; t			= 100 °С; v	= 1,1 м/с
70	46	150	0,77	0,77	46	44	2500	2600
60	85	90	0,71	0,71	51	49	2450	2400
40	158	168	0,57	0,58	60	58	2000	2150
20	278	270	0,42	0,42	70	71	980	1150
10	295	305	0,33	0,33	78	76	750	950