Исследование тормозных режимов зарезонансных вибрационных транспортирующих машин

го момента нагрузки и момента сопротивления вызванного вращающимися дебалансными массами является актуальной.

Рассмотрим поведение АДВД в процессе торможения на примере динамической одномассовой вибрационной системы направленных колебаний (рисунок 1).

Уравнения движения представленной на рис. 1 вибрационной системы имеют вид [1, 2]:

<

( m + m , ( ® )) x + b x ( ю )x + k x ( ю )x = ^ m i R m i cos a + e )sin ю t ) + F ;

i = 1

( m + m( m ))y + b y ( ю ) y + k y ( ю ) y = ^ m i Rai i sln a + Dsin ^ t ) + N ;

i = 1

J i ^Ю = M ЭМ1 - M ВИБР1 - ^m0i^Ri g ^sln( ® t ) - M МЕХ1 " (2) dt

Уравнения (1) описывают движение грузо-несущего органа ВТМ согласно второму закону Ньютона, а уравнение (2) – закону равновесия моментов на валу i -го вибродвигателя.

В уравнениях (1-2) обозначено: a — угол наклона грузонесущего органа к горизонту; в -угол направления вынуждающей силы; m₁ – масса грузонесущего органа с расположенными на нем двигателями; m 1 ( m ) — масса груза, колеблющаяся в фазе с грузонесущим органом; m_0i – масса i -го дебаланса; R_i – эксцентриситет i -го дебаланса; g – ускорение свободного падения; y и x – смещение грузонесущего органа по осям Y и Х (вибросмещение); y = dy I dt и x = dx / dt — скорость грузонесущего органа по осям Y и Х ; y = d ² y / dt и x = d ² x I dt — ускорение грузонесущего органа по осям Y и Х ; b y ( ю ) и b_x ( ю ) -коэффициенты сопротивления системы по осям Y и X ; k_y ( ю ) и k_x ( ю ) - жесткости упругих связей по осям Y и X ; N и F – нормальная и касательная составляющие нагрузки от транспортируемого груза на грузонесущий орган; J_i – приведенный момент инерции i -го электродвигателя;

М_ЭМi – электромагнитный момент на валу i -го электродвигателя; М_МЕХi – момент сопротивления на валу i -го электродвигателя, обусловленный механическими потерями; М_ВИБРi – вибрационный момент на валу i -го электродвигателя; щ_i – частота вращения вала i -го электродвигателя; m ₀ i R i to i cos( a + в ) sin( to i t ) — проекция центробежной силы дебалансов на ось Х ; m ₀ , R . o . sin( a + e )sin( to i t ) — проекцияцентро-бежной силы дебалансов на ось Y ; m ₀ Rg sin( to i t ) - моменты сопротивления на валу i -го электродвигателя, вызванный весом дебаланса.

В случае системы с двумя степенями свободы вибрационный момент i -го вибродвигателя имеет две составляющие:

• 1.    M_ВИБPiY = F_xi ■ y — составляющая, обусловленная наличием смещения системы по оси Y и проекции центробежной силы i -го дебалансно-го вибродвигателя на ось Х , где F xi определяется по формуле:

• 2.    M ВивРх = F yi " x — составляющая, обусловленная наличием смещения системы по оси X и проекции центробежной силы i -го дебалансно-го вибродвигателя на ось Y , где F yi определяется по формуле:

• 3.    Результирующее выражение вибрационного момента, приложенного к валу i -го вибродвигателя, определяется следующей формулой:

F xi = m о i Rto i^{cos( a} + ^{e )sin( to} i t ).

Fyi = m0iRto/ sin(a + e)sin(toit)•

^M ВИБPi = ^Fxi ' y ^{+ F}yi "  ^X .

Процесс конденсаторного торможения осуществляется двумя ступенями с различными значениями емкости, либо может производиться одной из ступеней. Схема, обеспечивающая конденсаторное торможение, имеет небольшую постоянно подключенную емкость (1 ступень, служащая также для компенсации реактивной

мощности вибродвигателя в рабочем режиме) и подключаемую значительную емкость (2 ступень). Первая ступень обеспечивает начало торможения после отключения АДВД, а вторая – дальнейшее снижение скорости вибродвигателя в процессе торможения.

При торможении электромагнитные процессы в каждом АДВД описываются по формулам:

0 = R A i A

⁰ = ^RB i B

0 = R_Ci_C

0 = R a i a

0 = R b i b

0 = R c i c

+ d^A dt

+ d^B dt

+ d^C dt d^a , + dt ’

⁺ u CA ;

⁺ u CB ;

⁺ u CC ;

+

d ^b .

dt

+ d W c dt

;

•

Здесь обозначено:

R_A, R_B, R_C, R_a, R_b, R_c – активные сопротивления обмоток статора и приведенные активные сопротивления обмоток ротора; i_A, i_B, i_C, i_a, i_b, i_c – фазные токи статора и ротора в процессе торможения; у A , ^ _B , W_C , W_a , ¥ ь , ^ c — потокосцепления статорных и роторных обмоток в процессе торможения; u_CA, u_CB, u_CC – падение напряжения на тормозных конденсаторах в фазах двигателя.

Потокосцепление АДВД определяется выражением в матричной форме:

[ у ] = [ F ■ M ] x [ i ] , где ^[ у ^] = ^[ у ^ ,У в ,y C ,У а ,У ь ,У с ^{] -} матрица-столбец потокосцеплений; [ i ] = [i_A , i_B , i_C , i_a , i b , i_c ] – матрица-столбец токов; [ M ] – матрица ин-

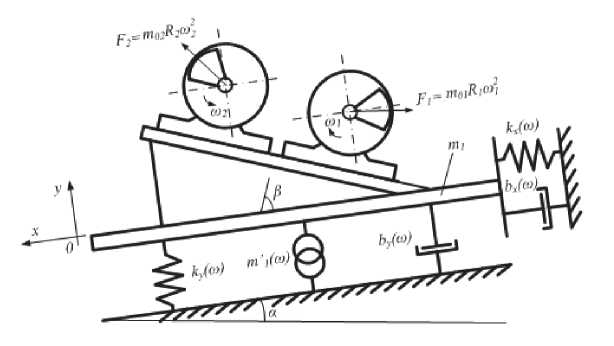
Рис. 1. Одномассовая вибрационная система

дуктивностей, F – коэффициент, относительной частоты самовозбуждения АДВД в процессе торможения.

Коэффициент относительной частоты самовозбуждения АДВД определяется выражением [3, 4]:

F =

f CL ^,

где f – частота питающего напряжения, С – эквивалентная емкость тормозных конденсаторов, L – эквивалентная индуктивность фазы двигателя.

Падение напряжения на тормозных конденсаторах в фазах двигателя определяется из выражений:

1 Г • u CA = CF J i A dt ;

'B = C ■ F J iBdt’

1 Г

ucc = c f J icdt’ где С – емкость тормозных конденсаторов в фазе двигателя.

Уравнение электромагнитного момента с учетом вышесказанного определяется:

_   Vs

МЭМ = — РМ\-(iAic + iBia + icib ) - (iAib + iBic + iCia )], где М – взаимная индуктивность; р – число пар полюсов АДВД.

Представленная система нелинейных дифференциальных уравнений эффективно решается с помощью вычислительной техники с использованием численных методов интегрирования и дифференцирования. Для этих целей была создана математическая модель рассматриваемой вибрационной системы и асинхронного дебалан-сного электродвигателя с конденсаторами в программной среде МВТУ 3.7, проведены исследования тормозных режимов работы вибрацион- ной транспортирующей машины.

Основные параметры вибротранспортера: m=113кг, b_y=b_x=1150Н/м, k_y=k_x=316000 кг*м/с², а =10 * , в =40 * . Тип вибродвигателя ИВ - 105 -2 на базе АДВД с параметрами: Р_Н=1,1 кВт, n_Н=1450 об/мин, R₁=9,53 Ом, L₁=0,037 Гн, R₂=5,619 Ом, L₂=0,029 Гн, L_m=0,447 Гн, J_д=0,0026 кг/м², m₀=1,5 кг, r₀=0,05 м. Параметры пускового устройства: 1 ступень – С_т1=60 мкФ , 2 ступень – С =200 мкФ .

т2

На рис. 2 представлены расчетные осциллограммы изменения частоты вращения АДВД и амплитуды колебаний ВТМ по оси Y при выбеге. Из осциллограмм частоты вращения можно заключить, что изменение скорости от номинального значения до нуля происходит за достаточно длительный период времени. За это время амплитуда колебаний машины достигает максимальных значений в области резонансной частоты системы ( а _рез=¹5^2,8 с^-1 ).

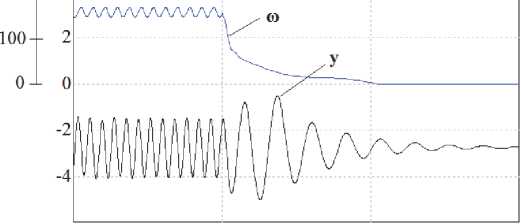
На рис. 3 представлены характеристики изменения частоты вращения АДВД и амплитуды колебаний ВТМ по оси Y при одноступенчатом конденсаторном торможении (2 ступень). Очевидно, что влияние отрицательного тормозного момента благоприятно сказывается на времени торможения, уменьшая последнее. В результате значения максимальных амплитуд машины при прохождении области резонанса значительно уменьшаются, что может положительно сказаться на надежной работе вибрационной транспортирующей машины.

На рис. 4 показаны характеристики изменения частоты вращения АДВД и амплитуды колебаний ВТМ по оси Y при двухступенчатом конденсаторном торможении (1 и 2 ступени). Из рисунка видно, что время торможения при данном типе торможении существенно сократилось. А максимальные резонансные амплитуды колебаний ВТМ практически отсутствуют, тем самым, исключаются критические условия работы транспортера.

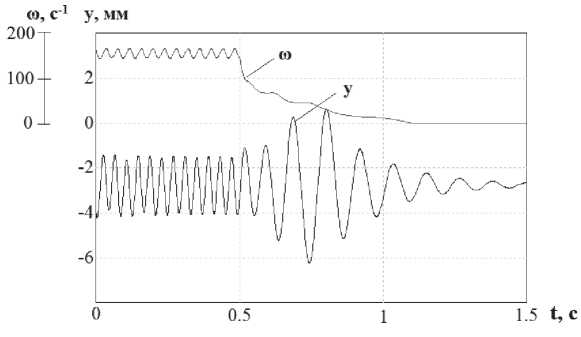
Рис. 2. Частота вращения АДВД и смещение системы по оси Y при выбеге

(О, С"1 у, мм

0                   0.5                   1                   1.5 t, с

Рис. 3. Частота вращения АДВД и смещение системы по оси Y при конденсаторном торможении (2 ступень)

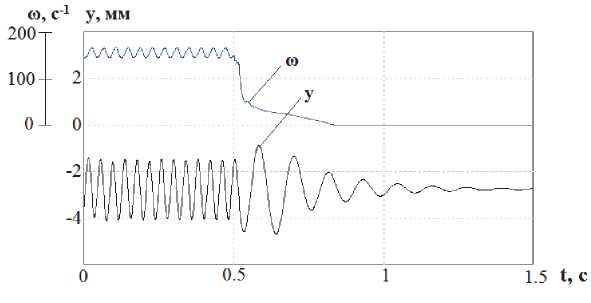
Рис. 4. Частота вращения АДВД и смещение системы по оси Y при конденсаторном торможении (1 и 2 ступени)

ВЫВОДЫ

• 1.    Конденсаторное торможение АДВД ВТМ позволяет существенно сократить время торможения и максимальные резонансные амплитуды колебаний машины, исключив тем самым неблагоприятные режимы ее работы.

• 2.    Двухступенчатое конденсаторное торможение АДВД ВТМ обладает более высокой эффективностью по сравнению с одноступенчатым торможением. Данное обстоятельство связано с тем, что тормозной момент, прикладываемый к АДВД, при двухступенчатом торможении при-

• сутствует практически на всем протяжении процесса торможения машины.