Исследование тороидального резонатора ускорительного СВЧ-ионного двигателя

При поддержке Российского научного фонда на материально-технической базе научноисследовательской лаборатории ОмГТУ «Двигательные установки микротяги малых космических аппаратов» (НИЛ «ДУМИТ МКА») ведётся разработка ускорительного СВЧ-ионного микродвигателя (УМД). В конструкции предложен способ резонаторного ускорения ионизированного газа в переменном электрическом поле [1]. Авторами был изготовлен прототип УМД, структурная схема которого представлена на рис. 1. В данном прототипе реализована схема двойного последовательного ускорения ионизированного газа: постоянным и переменным электрическими полями. Источником электромагнитной энергии является твердотельный СВЧ-автогенератор (поз. 8), установленный в цилиндрический резонатор (поз. 11). Ускорительные элементы прототипа представлены в виде электродов ионно-оптической системы (ИОС) постоянной разности потенциалов (поз. 1 и 4) и перфорированными торцевыми крышками (поз. 5 и 6) двух цилиндрических резонаторов (поз. 12 и 13). Соосно установленные цилиндрические резонаторы (поз. 12 и 13) образуют тороидальный резонатор с ускоряющим зазором величиной s .

Охлаждение платы СВЧ-автогенератора осуществляется элементом Пельтье (поз. 7) с отводом тепла на корпус прототипа. В прототипе реализовано внешнее энергопитание, поэтому внутри внешнего резонатора (11) установлен фильтр низких частот (ФНЧ), и электро- – 858 –

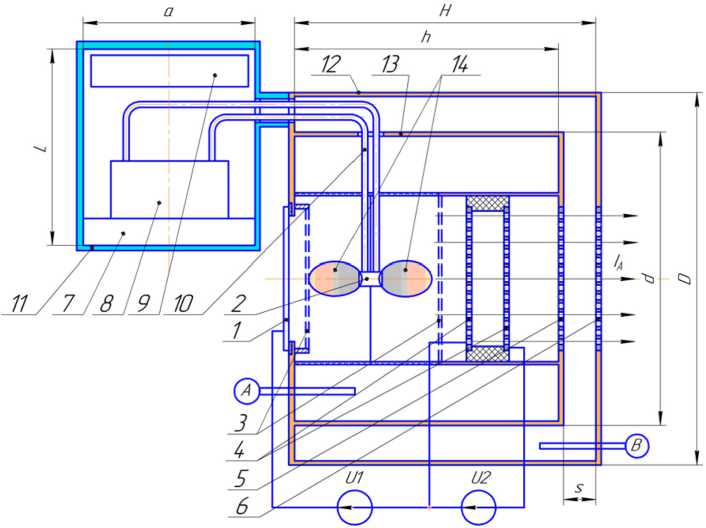
Рис. 1. Структурная схема прототипа УМД

Fig. 1. Block diagram of the prototype of the accelerator micro thruster ды ИОС изолированы от области высокочастотных колебаний защитными сетками (поз. 3). Данные конструктивные особенности позволяют избежать выхода СВЧ-энергии из полости резонаторов по силовым проводам. Источником рабочего тела – плазмы, служит высокочастотный ёмкостной зазор (поз. 2), образованный сетчатыми электродами. Подвод энергии от автогенератора к ёмкостному зазору осуществляется двухпроводной линией связи (поз. 10). Линия связи соединяет воедино все три резонатора (поз. 11–13) прототипа. Плазма, генерируемая в высокочастотном зазоре (2), принимает гантелевидную форму (поз. 14). Подача номинального напряжения U 1 приводит к извлечению отрицательной компоненты плазмы на электрод (поз. 1) ИОС (в экспериментах рабочий газ – азот). В полости газоразрядной камеры образуется положительный объёмный заряд, и ионы вытесняются в зазор между электродами (поз.4) ИОС. Номинальное напряжение U 2 регулируемое. В ИОС осуществляется первичное ускорение ионов. Из первого ускоряющего промежутка ионы попадают в ускоряющий зазор тороидального резонатора, где получают дополнительный прирост кинетической энергии (вторичное ускорение).

Постановка задачи

Целью исследования является определение величины переменного ускоряющего напряжения, возбуждаемого электромагнитной волной в ёмкостном зазоре тороидального резонатора. Следует отметить, что экспериментальное определение напряженности переменного электрического поля проблематично вследствие малых величин ускоряющих зазоров, куда физически невозможно установить датчик прибора измерения уровня электромагнитного поля.

Методика расчёта тороидального ускорителя основана на методике расчёта полицилин-дрического ускорителя (ПЦУ) [2]. Сама методика, в свою очередь, сформирована на классическом подходе представления тороидального резонатора как замкнутого RC-контура.

Напряжение в зазоре резонатора можно определить из выражения:

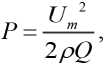
где Um – амплитуда напряжения на зазоре, а ρ = 1/ωС0 – характеристическое сопротивление резонатора на частоте ω; Q –добротность резонатора.

Отсюда

и„=4Г^р

Трудоёмкой в определении величиной является мощность, рассеиваемая в полости резонатора. Определение величины Р не обходится без экспериментальных замеров. Данная мощность есть мощность электромагнитного излучения плазмогенератора. Так как конструкция УМД – это закрытая металлическая оболочка, то вся электромагнитная энергия, излучаемая СВЧ-генератором, поглощается резонатором.

Частотный анализ резонаторов

Частоты резонаторов определялись анализатором спектра Arinst SSA-TG R 2 (волновое сопротивление R вол = 50 Ом). Приёмником сигнала служила штыревая антенна длиной 5 см и диаметром 2 мм. Данная конструкция позволяла ввести антенну через малое отверстие в полость тороидального резонатора прототипа УМД. Частотный анализ проводился в режиме работы прототипа без разряда на электродах СВЧ-автогенератора.

В табл. 1 приведены замеренные значения частот и уровня сигнала у выходного разъёма СВЧ-автогенератора, помещённого в цилиндрический резонатор без установленного тороидального резонатора. СВЧ-автогенератор расположен в резонаторе диаметром 80 мм, высотой 100 мм.

Резонансные частоты собственных колебаний в цилиндрическом резонаторе для видов Н mnp и Е mnp (m – число полных периодов стоячих волн поля, укладывающихся по окружности резонатора (азимутальное направление), n – число полупериодов стоячей волны поля, укладывающихся по диаметру резонатора 2·a (радиальное направление), р – число полупериодов поля стоячей волны, укладывающихся на длине резонатора l (продольное направление)), можно определить по формулам [3]:

Таблица 1. Измеренные значения частот и мощностей автогенератора в цилиндрическом резонаторе

Table 1. Measured values of frequencies and capacities of an autogenerator in a cylindrical resonator

№ гармоники	Частота, МГц	Уровень сигнала, дБм	№ гармоники	Частота, МГц	Уровень сигнала, дБм
1	429.65	10	7	3002.04	-31.4
2	-	-	8	3430.73	-35.9
3	1286.7	-24	9	3859.43	-37.5
4	1715.59	-35.6	10	4288.13	-41
5	2144.45	-28	11	4716.84	-58
6	2573.32	-37

– для колебаний видов Н mnp

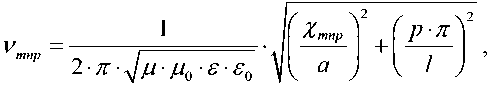
– для колебаний вида Е mnp

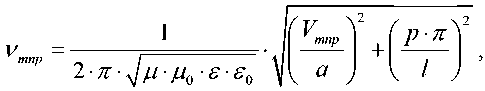
где ε₀ и μ₀ – электрическая и магнитная постоянные; ε и μ – электрическая и магнитная проницаемости среды в резонаторе; χmnp и Vmnp – корни с номером m функции Бесселя порядка n (табл. 2).

Согласно формулам (3) и (4) для внешнего цилиндрического резонатора были получены частоты, представленные в табл. 3 (при р = 0) и табл. 4 (при р = 1).

Проблемой в расчётном определении частоты внешнего цилиндрического резонатора является неизвестность в части относительной магнитной проницаемости среды в резонаторе μ и относительной диэлектрической проницаемости ε , так как внутри резонатора расположены плата СВЧ-автогенератора, ФНЧ, система охлаждения на элементе Пельтье и корпусные элементы. Соответственно, подкоренное выражение в формулах (3) и (4) μ·ε ≠ 1 и частоты резонатора могут быть намного ниже.

Таблица 2. Корни χ mnp и V mnp функции Бесселя порядка n

Table 2. Roots χ mnp and V mnp Bessel functions of order n

m	n	0	1	2
χ mnp
1		3.832	1.84	3.054
2		7.016	5.335	6.705
mnp
1		2.405	3.832	5.135
2		5.52	7.016	8.417

Таблица 3. Частоты колебаний видов Н_mnp и Е_mnp при р = 0 ( μ = 1, ε = 1)

Table 3. The oscillation frequencies of the Н mnp and Е mnp types at р = 0 ( μ = 1, ε = 1)

m               n	0	1	2
Н mnp , МГц
1	4570	2195	3642
2	8368	6363	7997
Е mnp , МГц
1	2868	4570	6124
2	6584	8368	10040

Таблица 4. Частоты колебаний видов Н_mnp и Е_mnp при р =1 ( μ =1, ε =1)

Table 4. The oscillation frequencies of the Н_mnp and Е_mnp types at р =1 ( μ =1, ε =1)

m	n	0	1	2
Н mnp , МГц
1		4810	2657	3939
2		8501	6537	8136
Е mnp , МГц
1		3236	4810	6305
2		6752	8501	10150

При отношении l/а ≥ 2.03 (длинные резонаторы) низшим видом колебаний будет Н 111 . Данное отношение для применяемого резонатора составляет 2.5. Частота низшего вида колебаний при μ·ε = 1 по выражению (3) составляет 2657 МГц.

Далее были получены частоты тороидального резонатора (табл. 5) и цилиндрического резонатора, находящегося внутри тороидального резонатора (табл. 6). В этих замерах к внешнему

Таблица 5. Измеренные значения частот и мощностей автогенератора в тороидальном резонаторе

Table 5. Measured values of frequencies and capacities of an autogenerator in a toroidal resonator

№ гармоники	Частота, МГц	Уровень сигнала, дБм	№ гармоники	Частота, МГц	Уровень сигнала, дБм
1	248.45	-22	9	2236	-55
2	496.92	-46	10	2484.79	-45
3	745.54	-54	11	2733.3	-47
4	-	-	12	2981.82	-65
5	1242.36	-61	13	3230.38	-67
6	1490.97	-63	14	3478.79	-63
7	1739.43	-63	15	3727.28	-50
8	1987.92	-55

Таблица 6. Измеренные значения частот и мощностей автогенератора во внутреннем цилиндрическом резонаторе

Table 6. Measured values of frequencies and capacities of an autogenerator in an internal cylindrical resonator

№ гармоники Частота, МГц Уровень сигнала, дБм № гармоники Частота, МГц Уровень сигнала, дБм 1 244.72 -15.9 7 1712.67 -63 2 489.36 -52 8 1957.31 -62 3 734.01 -27.4 9 2201.95 -39.6 4 978.5 -34.7 10 2446.59 -48 5 1223.38 -30 11 2687 -44 6 1460 -53 12 2934 -58 цилиндрическому резонатору с автогенератором через штепсельный разъем присоединялась ускорительная часть двигателя, состоящая из медных резонаторов, содержащих пластиковые элементы конструкции (АБС-пластик) и ёмкостный СВЧ-автогенератор. Замеры проводились через малые отверстия в торцевых стенках обоих резонаторов (поз. А и В, рис. 1). От штепсельного разъёма линия связи проходит через пространство между стенками резонаторов и вводится в полость внутреннего резонатора к ёмкостному излучателю.

Расчётная резонансная частота тороидального резонатора при μ·ε = 1 равна [4]:

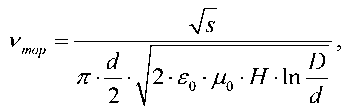
где D = 140 мм – диаметр тороидального резонатора; d = 98 мм – диаметр внутреннего цилиндрического резонатора; H = 62 мм – высота тороидального резонатора; s = 2 мм – длина ускоряющего зазора.

По формуле (5) резонансная частота тороидального резонатора составила 404 МГц.

По формулам (3) и (4) для внутреннего резонатора можно получить значения частот при μ·ε = 1 и соотношении l/а = 1.2. В этом случае р = 0 и низшим видом колебаний будет Е 010 .

Данные сведены в табл. 7.

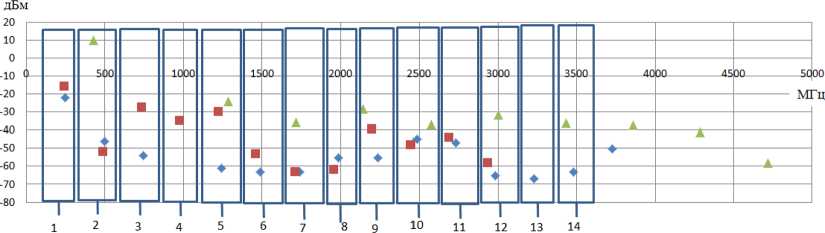
На рис. 2 представлена сводная диаграмма частот и их мощностей для всех трёх резонаторов.

На диаграмме выделены области близких частот резонаторов. Область 1 соответствует основной частоте внутреннего цилиндрического и тороидального резонаторов.

Область 2 – это основная частота цилиндрического внешнего резонатора. Видно, что уровень мощности сигнала на основной частоте наивысший для всех трёх резонаторов.

Области 5, 7, 9, 10, 12, 14 для внешнего цилиндрического резонатора имеют практически одинаковый уровень мощности, что может указывать на резонансные эффекты в полости резонатора на частотах от 1290 МГц до 3860 МГц. Сопоставление замеренных (табл. 1) и теоретически полученных (табл. 2) частот внешнего цилиндрического резонатора в области совпадения отражено в табл. 8. Там же представлены замеренные мощности сигналов.

Таблица 7. Частоты колебаний видов Н_mnp и Е_mnp внутреннего цилиндрического резонатора при р = 0 ( μ = 1, ε = 1)

Table 7. The oscillation frequencies of the Н_mnp and Е_mnp types of the internal cylindrical resonator at р = 0 ( μ = 1, ε = 1)

m               n	0	1	2
Н mnp , МГц
1	3656	1756	2914
2	6694	5090	6398
Е mnp , МГц
1	2295	3656	4900
2	5267	6694	8031

♦ Тороидальный резонатор ■Внутренний цилиндрический резонатор Внешний цилиндрический резонатор

Рис. 2. Диаграмма частот и их мощностей тороидального, цилиндрического внутреннего и цилиндрического наружного резонаторов

Fig. 2. Diagram of frequencies and their capacities of toroidal, cylindrical inner and cylindrical outer resonators

Таблица 8. Замеренные и расчётные частоты внешнего цилиндрического резонатора и их соотношение

Table 8. Measured and calculated frequencies of external cylindrical resonators and their ratio

f теор , МГц	2195	2657	2868	3236	3642	3939	4570
f зам , МГц	2144.45	2573.32	3002.04	3430.73	3959.43	4288.13	4716.84
Δf ,%	2.3	3.2	4.5	5.7	5.7	8.2	3.2
Р , дБм	-28	-37	-31.4	-35.9	-37.5	-41	-58

Из табл. 8 видно, что приближение частоты гармоники к собственной частоте резонатора выражается в удержании мощности сигнала на более высоком уровне. Исключением из данной зависимости является частота 4716.84 МГц.

Области 3–5, 9 на рис. 2 показывают реакцию внутреннего цилиндрического резонатора на частоты 734.01 МГц, 978.5 МГц, 1223.38 МГц и 2201.95 МГц при совместной работе с тороидальным резонатором. Видно, что реакция тороидального резонатора на эти гармоники отсутствует. В областях 2, 10 и 11 видна реакция тороидального резонатора на частоты 496.92МГц, 2484.79 МГц и 2733.3 МГц при отсутствии реакции внутреннего цилиндрического резонатора. Напомним, что расчётная резонансная частота тороидального резонатора составила 404 МГц. Сравнивать расчетные и замеренные частоты внутреннего цилиндрического резонатора нет необходимости, так как внутренний цилиндрический резонатор является реактором с чередующимися диэлектрическими и металлическими элементами конструкции.

Опыт совместного частотного исследования резонаторов при наличии общей колебательной линии и большого числа гармоник позволяет определить область резонансных частот каждого резонатора по величине их реакции на гармоники.

Среднюю мощность сигнала, рассеиваемого в стенках тороидального резонатора можно определить по формуле:

где | U | – модуль комплексного напряжения сигнала в резонаторе; Rmop – сопротивление материала стенок резонатора.

Для нахождения модуля комплексного сопротивления требуется определить входное сопротивление штыревой антенны для каждой гармоники, присутствующей в тороидальном резонаторе. Для этих целей использовалась программа для расчёта и анализа антенн MMANA-GAL. В табл. 9 представлены результаты моделирования.

По показаниям анализатора спектра (с учётом ослабления сигнала внутренним аттенюатором в 20 дБ) (табл. 5) и по входному сопротивлению принимающей антенны (табл. 9) можно получить значение напряжения в резонаторе:

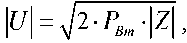
где PBm – уровень мощности сигнала в тороидальном резонаторе в Вт при учёте ослабления в 100 раз; Z = R + R_6O4+i-X – входное сопротивление принимающей линии.

Сопротивление стенок тороидального резонатора обусловлено скин-эффектом и выражается формулой:

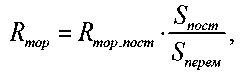
'ипгт

где топ пост P mop.пост   r q

– электрическое сопротивление при постоянном токе эквивалентного пост

провода, чья площадь боковой поверхности равна площади внутренней поверхности тороидального резонатора; ρ – удельное электрическое сопротивление материала резонатора; Lпост – длина эквивалентного провода; Sпост – площадь поперечного сечения эквивалентного провода при постоянном токе;

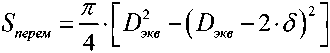
– площадь поперечного сечения экви- валентного провода при переменном токе; Dэкв – диаметр сечения эквивалентного провода;

Таблица 9. Результаты расчёта активного и реактивного сопротивлений штыревой антенны в программе MMANA

Table 9. The results of the calculation of the active and reactive resistances of the antenna in the MMANA program

№ гармоники	Частота, МГц	R , Ом	i·X , Ом	№ гармоники	Частота, МГц	R , Ом	i·X , Ом
1	248.45	0.339	-3076	9	2236	34.423	-125.9
2	496.92	1.273	-1410	10	2484.79	47.365	-69.809
3	745.54	2.824	-879.83	11	2733.3	65.259	-16.697
4	-			12	2981.82	89.936	34.906
5	1242.36	8.218	-459.9	13	3230.38	126.07	86.76
6	1490.97	12.414	-348.61	14	3478.79	179.4	137.084
7	1739.43	17.793	-259.56	15	3727.28	258.783	179.67
8	1987.92	24.916	-187.63

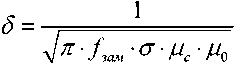
– глубина скин-слоя; fзам – частота электромагнитной волны в резона- торе; σ – электрическая проводимость материала стенок резонатора; μс – магнитная проницаемость материала стенок резонатора.

По формуле (6) были получены значения мощности, рассеиваемой в стенках тороидального резонатора. Данные представлены в табл. 10.

Таблица 10. Расчётные значения рассеиваемой в тороидальном резонаторе мощности электромагнитной волны

Table 10. Calculated values of the electromagnetic wave power dissipated in a toroidal resonator

№ гармоники	Частота, МГц	Р тор , Вт	№ гармоники	Частота, МГц	Р тор , Вт
1	248.45	1.269	9	2236	1.046·10–5
2	496.92	1.639·10–3	10	2484.79	7.839·10–5
3	745.54	1.325·10–4	11	2733.3	4.584·10–5
4	-	-	12	2981.82	8.615·10–7
5	1242.36	1.077·10–5	13	3230.38	7.108·10–7
6	1490.97	4.741·10–6	14	3478.79	2.342·10–6
7	1739.43	3.325·10–6	15	3727.28	6.036·10–5
8	1987.92	1.478·10–5

Видно, что основная частота несёт основную энергию, тогда как энергии гармоник пренебрежимо малы. Суммарное значение мощности, рассеиваемой в резонаторе, составило 1.271 Вт.

Калориметрическое исследование тороидального резонатора

В практике для измерения СВЧ-мощности применяется калориметрический метод. Он нашёл широкое применение благодаря простоте превращения энергии электрического тока в теплоту [5]. В рамках экспериментального исследования мощности, рассеиваемой в тороидальном резонаторе, была проведена работа по калориметрическим исследованиям корпуса прототипа ускорительного СВЧ-ионного двигателя. Работа проводилась с применением тепловизора Testo 872 + 605i в условиях вакуумной камеры. Производилась съёмка торцевой поверхности тороидального резонатора от момента подачи электромагнитной энергии до установления теплового равновесия системы.

На рис. 3 представлено изображение с камеры тепловизора Testo 872 + 605i.

На рис. 3 позициями обозначены: 1 – тороидальный резонатор; 2 – внешний резонатор автогенератора; 3 – перфорированная сетка тороидального резонатора; 4 – разъём замера частоты тороидального резонатора.

На рис. 4 представлены термографические изображения торцевой поверхности тороидального резонатора в начальный момент, когда отсутствует подача электромагнитной энергии,

Рис. 3. Вид на торцевую стенку тороидального резонатора в вакуумной камере

Fig. 3. View of the end wall of a toroidal resonator in a vacuum chamber

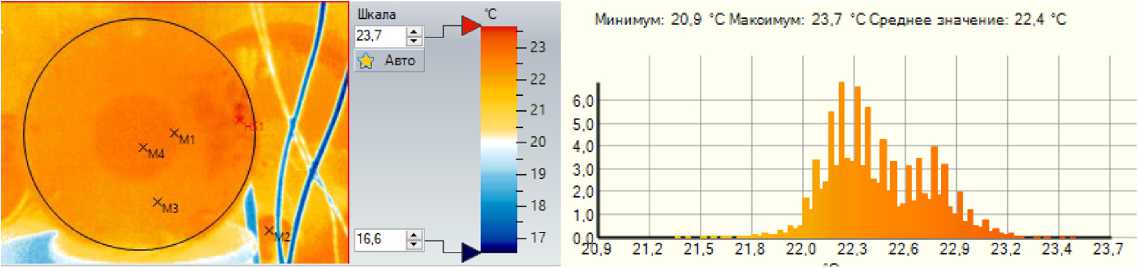
Термограмма при t=0 сек (генератор выключен)

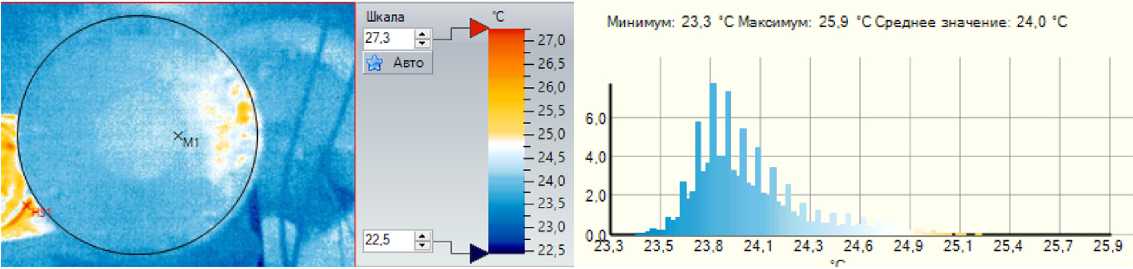
Термограмма при t=622 сек

Рис. 4. Примеры термограмм торцевой стенки тороидального резонатора

Fig. 4. Examples of thermograms of the end wall of a toroidal resonator и в конечный момент, когда наблюдается установившееся тепловое равновесие системы, а также отображены цветовые тепловые шкалы и гистограммы распределения температуры в выделенных на термограммах областях.

В табл. 11 указаны температуры поверхности торцевой стенки тороидального резонатора в зависимости от времени измерения.

Данные из табл. 11 можно представить в виде диаграммы (рис. 5).

Расчёт проводился из условия, что внешний и внутренний резонаторы нагреваются равномерно. По геометрическим размерам, толщине стенок резонаторов (1 мм) и плотности материала (медь) была определена масса резонаторной сборки. Она составила 0.617 кг. Для восходящей прямой нагрева (до точки t = 347 сек) определялась тепловая мощность:

'   = т -с тепл рез ;

Т -т

кон _____ нач

А/

Таким образом, согласно калориметрическому исследованию мощность СВЧ-потерь в полости резонатора составила 0.97 Вт при энергопотреблении генератора 3 Вт.

Для определения характеристического сопротивления резонатора на основной частоте необходимо найти электрическую ёмкость резонатора. Емкость, на которую нагружен резонатор, определяется как емкость плоского конденсатора, образованного круглыми крышками на внутреннем и внешнем цилиндрах, и ёмкость, образованная цилиндрическими поверхностями резонаторов:

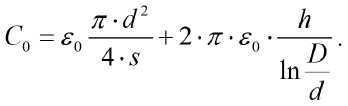
Добротность тороидального резонатора на основе расчёта коаксиального резонатора равна [6]:

,____ l(2^.£ + sin(2.^£))

2 = 875 • д/Л -102 ■                  2(11)

,          1 ( pctg^-pX’

15 p-ctg(p-L) d (          у’ где β = 2π/λ – волновое число; λ = с/fтор – длина волны основной частоты в резонаторе.

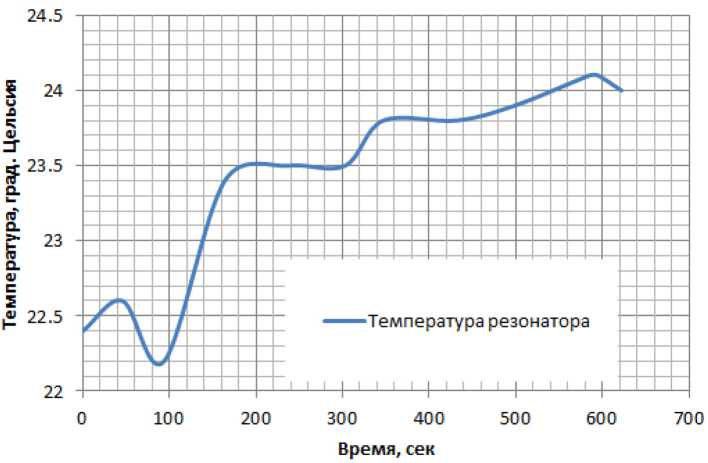
Рис. 5. Диаграмма роста температуры поверхности тороидального резонатора

Fig. 5. Diagram of the temperature rise of the surface of the toroidal resonator

Таблица 11. Температуры поверхности тороидального резонатора в зависимости от времени

Table 11. Toroidal resonator surface temperatures as a function of time

t, сек	0	46	94	164	238	303	347	432	499	585	595	622
T, 0C	22.4	22.6	22.2	23.4	23.5	23.5	23.8	23.8	23.9	24.1	24.1	24

Таблица 12. Расчётные параметры тороидального резонатора прототипа

Table 12. Сalculated parameters of the prototype toroidal resonator

f тор , МГц	λ , м	С 0 , пФ	ρ , Ом	Q	U , В
248.45	1.207	42.907	14.93	6589	436.8

Результаты расчёта тороидального резонатора прототипа УМД при учете мощности СВЧ-потерь, определённых калориметрическим методом, представлены в табл. 12.

Обсуждение результатов

Авторами была проведена работа в части определения ускоряющего напряжения в зазоре тороидального резонатора. Работа имеет практическое значение, так как направлена на исследование выходных характеристик прототипа ускорительного СВЧ-ионного двигателя. В ходе исследования экспериментальным путем определялась мощность СВЧ-потерь в полости тороидального резонатора при безразрядном режиме работы прототипа. Данная величина была найдена частотным и калориметрическим методами. Первый метод показал значение мощности потерь 1.271 Вт, второй метод – 0.97 Вт. Расхождение результатов двух экспериментальных методов составила ≈24 %. Величина ускоряющего напряжения, рассчитанная для безразрядного режима работы прототипа по калориметрическим данным, составила 436.8 В при энергопотреблении СВЧ-автогенератора 3 Вт. Неоспоримым преимуществом калориметрического метода является простота его реализации и математического аппарата. Однако тепловой метод не применим в случае разрядного режима работы прототипа. Возникновение проводящей среды между электродами плазмогенератора приводит к потерям энергии электромагнитного поля в плазме (нагрев плазмы). Также вследствие рекомбинации возникает излучение оптического диапазона. При этом термографирование стенок резонатора будет отражать суммарный нагрев от волн ВЧ/СВЧ-диапазона и оптического диапазона. Ускоряющее напряжение в резонаторе обусловлено только действием микроволнового излучения. Таким образом, в случае разрядного режима работы прототипа УМД калориметрический метод будет давать завышенное значение мощности СВЧ-потерь. Частотный метод, являясь более громоздким, лишён данного недостатка. В целом в разрядном режиме работы прототипа величина ускоряющего напряжения в зазоре тороидального резонатора будет ниже, нежели в безразрядном режиме.

Также в ходе исследования было установлено, что, несмотря на густой спектр гармоник, 99 % энергии в тороидальном резонаторе передаётся на основной частоте. Остальные частоты являются индикаторными, т.е. отражают резонансные области тех или иных пассивных элементов колебательного контура.

Заключение

Расхождение в результатах калориметрического и частотного методов исследования мощности СВЧ-потерь в тороидальном резонаторе составило не более 24 %. Область применения частотного метода определения мощности СВЧ-потерь заключается в установлении значений – 869 – ускоряющего напряжения при работе прототипов УМД в условиях вакуумной камеры при наличии в рабочих полостях ионизированной газовой среды.