Исследование управляемого сверхвысокочастотного жидкокристаллического фазовращателя

Перестраиваемые фазовращатели являются важнейшими элементами фазированных антенных решеток радиолокационных станций, они используются также в современных системах связи, в различной измерительной и специальной радиоаппаратуре. Ранее была предложена [1] и позже исследована [2] резонансная конструкция микрополоскового электрически управляемого жидкокристаллического фазовращателя. Фактически такой фазовращатель представляет собой микрополосковый фильтр, в котором в качестве подложки используется жидкий кристалл (ЖК). Благодаря наличию анизотропии диэлектрической проницаемости у ЖК в такой конструкции появляется возможность управления фазой электромагнитных СВЧ-колебаний путем изменения напряжения, прикладываемого между микрополосковыми проводниками и экраном. При этом размеры резонансной конструкции получаются существенно меньшими, чем у фазовращателя с той же величиной управляемого фазового сдвига, но выполненного в виде микрополосковой линии передачи, заполненной ЖК. Фазовращатель резонансной кон

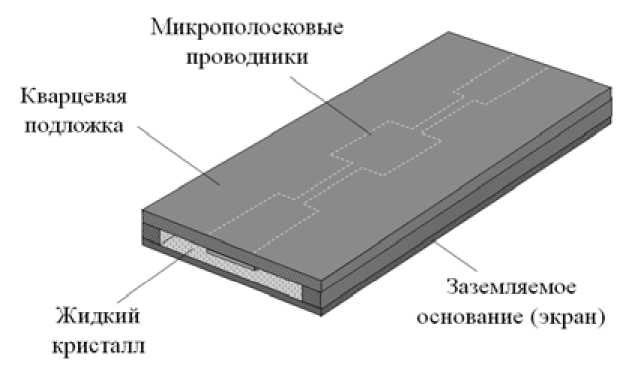
Рис. 1. Конструкция и топология проводников пятирезонаторного фазовращателя струкции может иметь центральную частоту полосы пропускания от единиц до десятков и теоретически до сотен гигагерц, так как анизотропия ЖК сохраняется и в оптическом диапазоне частот. На рис. 1 показана конструкция фазовращателя, состоящего из пяти резонаторов.

Подложкой фазовращателя служит жидкий кристалл, который удерживается силами поверхностного натяжения между верхним нерегулярным проводником и нижним – экраном. Такую конструкцию несложно реализовать, изготовив, например, нерегулярный полосковый проводник на подложке из кварца. Вход и выход фазовращателя подключаются к внешним линиям передачи с волновым сопротивлением 50 Ом.

Результаты теоретических исследований

Как показали проведенные ранее исследования [2], в резонансной конструкции фазовращателя величина управляемого фазового сдвига зависит, в первую очередь, от следующих параметров: относительной ширины полосы пропускания устройства, количества резонаторов в нем и анизотропии диэлектрической проницаемости ЖК. Однако, полученные результаты носили качественный характер, а систематических исследований резонансной конструкции не проводилось. В связи с этим важным является получение аналитической зависимости величины управляемого фазового сдвига резонансного фазовращателя от его основных конструктивных и электрических параметров.

Введем следующие обозначения: величина управляемого фазового сдвига - А ф, количество резонаторов в фазовращателе - n , ширина полосы рабочих частот фазовращателя - g f, ширина полосы пропускания устройства – ∆ f , значения продольной и поперечной компонент действительной части диэлектрической проницаемости ЖК - 8ц и е_± , анизотропия диэлектрической проницаемости - А 8= 8ц - 8_±, среднее значение диэлектрической проницаемости ЖК -⁸= (⁸н^{- 8} ± )^/2-

Получим выражение, связывающее относительную ширину полосы пропускания фильтра А fIf > с относительной шириной полосы рабочих частот устройства g f ] f , . Предположим, что при среднем значении диэлектрической проницаемости ЖК устройство имеет центральную

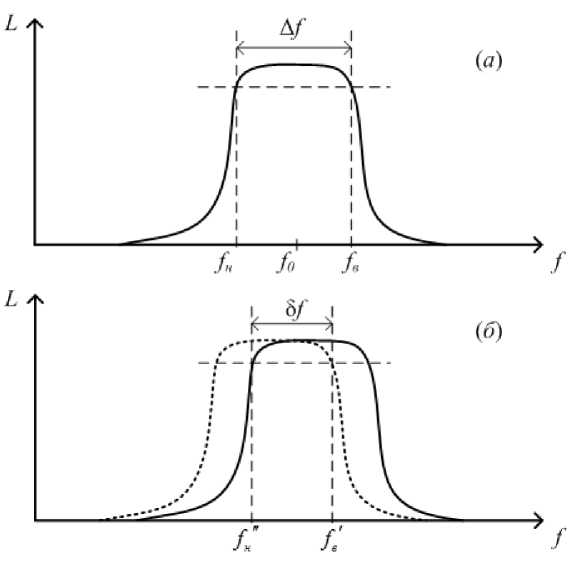
Рис. 2. Амплитудно-частотная характеристика устройства при среднем значении диэлектрической проницаемости ЖК ( а ) и предельных значениях е ( б )

частоту полосы пропускания f₀ и абсолютную ширину полосы пропускания А/ по уровню -3 дБ (рис. 2 а ). Тогда при изменении диэлектрической проницаемости ЖК под действием управляющего поля, будет происходить сдвиг полосы пропускания на амплитудно-частотной характеристике (АЧХ), однако при этом существует область рабочих частот устройства δ f , в пределах которой прямые потери прошедшего сигнала остаются минимальными и почти постоянными, в то время как фаза пошедшего сигнала существенно изменяется (рис. 2 б ).

Пусть под действием управляющего поля диэлектрическая проницаемость ЖК приняла максимально возможное значение Ей = е + ^^ , тогда центральная частота полосы пропускания ¹¹                      2

ε станет равной j0 = j0    , а верхняя и нижняя частоты полосы пропускания fs и fH , соот- ветственно. В отсутствие управляющего поля диэлектрическая проницаемость ЖК уменьша- е ется до е, = е -п% . При этом центральная частота становится равной f0 - f0-т=, а верхняя '2                                                                          е± и нижняя граничные частоты fe” и fH” соответственно (рис. 2б). Следует отметить, что при перестройке из-за изменения коэффициентов связи между резонаторами меняется и ширина полосы пропускания устройства, однако это изменение мало (несколько процентов), и им в первом приближении можно пренебречь.

Запишем выражение для ширины полосы рабочих частот фазовращателя:

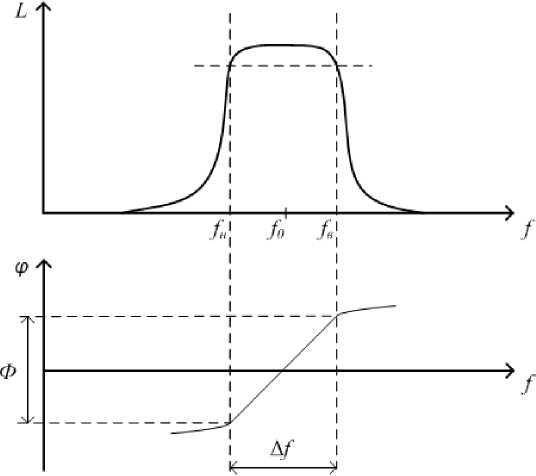
Рис. 3. Амплитудно-частотная и фазо-частотная характеристики полосового фильтра

f )        ^A f )

оf = f -Jh, = l f0 +— l-l f0 —— l = f0 -f0 +Af(1)

V ² J V ² J

Подставляя выражения для f ‘ и f 0", получим:

5f = f,    - f о -t^ + A f.(2)

^£ ±

Разделив на f , перейдем к относительным величинам: г г

5Ш, =^-^1 + АШ,.(3)

Данная формула позволяет при известной анизотропии ЖК и заданной относительной ши^рине полосы рабочих частот фазовращателя 3 f/^f > найти необходимую относительную ширину полосы пропускания устройства как фильтра A f If > .

Будем считать, что в полосе пропускания ∆f устройства фаза изменяется линейно (что верно в первом приближении для оптимально настроенной конструкции) на величину Φ (рис. 3).

Тогда зависимость набега фазы от частоты будет в общем случае описываться формулой

^Ф

ф ( f ) = k ( f - f 0 ) + d ф , где f , и d ф - константы, а коэффициент пропорциональности k = а_ .

При изменении центральной частоты от f ‘ до f ‘ разность набега фазы в рабочей полосе частот составит Аф = k ( f ‘ - f ‘ ). Подставляя выражения для k, f" и f ‘ , получим:

Аф =

^А f/^f > Цё ? Т⁸ !! J

Выражая Af If, через 3f If, с помощью формулы (3) и подставляя это значение в (4), по- лучим:

Аф =

Ф

( Г

V Е

Л

3 flf ) -

J

( Г V £

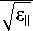
Е

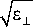
Вводя обозначение Зе =—^= —Д и подставляя значения для е _± и 8ц, получим: V^£ ± _х^е

Зе =

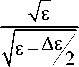
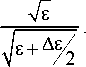
При этом следует учитывать, что 8 и А8 - это среднее значение и анизотропия эффективной диэлектрической проницаемости ЖК подложки. Величину изменения фазы Ф в полосе пропускания устройства ∆f при числе резонаторов n> 1 можно представить в виде Ф( n )=0.7×( n -1)×180º [3].

Подставляя (6) в (5), окончательно получаем:

Ф

АФ = 7777---.

³ f/^f ) + 1

Зе

Таким образом, формула (7) описывает зависимость величины управляемого фазового сдвига в рабочей полосе частот от количества резонаторов фазовращателя, относительной ширины полосы рабочих частот и величины анизотропии диэлектрической проницаемости ЖК.

Для проверки результатов были построены зависимости величины управляемого фазового сдвига от относительной ширины полосы рабочих частот исследуемого фазовращателя (рис. 4).

Кривые были рассчитаны в квазистатическом приближении в программе Microwave Office и по полученной формуле (7). Расчет проводили с количеством резонаторов n =5 и n =9 при анизотропии диэлектрической проницаемости ЖК Δε=0,4 и среднем значении диэлектрической проницаемости ε=3.

Зависимости, рассчитанные в квазистатическом приближении, состоят из двух участков. Это связано с тем, что относительная ширина первой полосы пропускания фазовращателя зависит от разности волновых сопротивлений микрополосковых линий, образующих его полуволновые отрезки (чем она больше, тем меньше ширина полосы), и для реализуемых на практике минимальных ширин полосковых проводников (100 мкм) не может быть достаточно мала. Известно, что абсолютные ширины первой и последующих полос пропускания фильтров на основе структуры фотонного кристалла одинаковы, а их центральные частоты кратны центральной частоте первой полосы пропускания f [5]. Поэтому относительная ширина полос пропускания с увеличением их номера N становится меньше и составляет А/ 7( N f) ). В связи с этим малые значения относительной ширины полосы рабочих частот исследуемого фазовращателя были реализованы на частотах второй полосы пропускания. Как видно из рис. 4, кривые, рассчитанные по полученной формуле (7) и в квазистатическом приближении, находятся в хорошем соответствии друг с другом, что позволяет сделать вывод об адекватности использованных приближений.

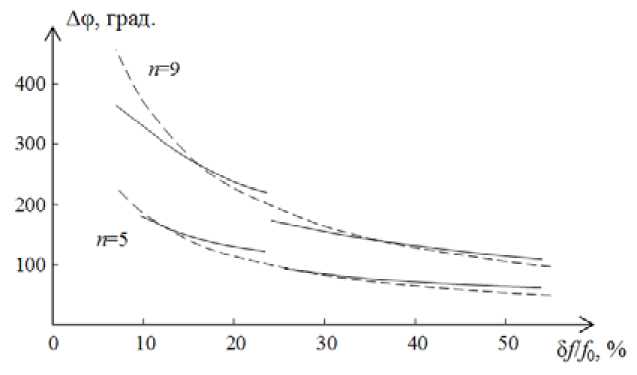
Рис. 4. Зависимость величины управляемого фазового сдвига от относительной ширины полосы рабочих частот резонансного фазовращателя (сплошные линии – расчет в программе Microwave Office , штриховые линии – расчет по полученной формуле)

Проведенные исследования показали, что исследуемую конструкцию фазовращателя целесообразно использовать при относительных рабочих полосах частот сигнала менее 20 %. В этом случае ее размеры, при прочих равных условиях, получаются существенно меньшими, чем у фазовращателя на основе согласованной линии передачи, заполненной ЖК.

Результаты экспериментальных исследований

Для экспериментальной проверки работоспособности исследуемой конструкции был синтезирован и изготовлен девятизвенный фазовращатель для реальной жидкокристаллической смеси с толщиной слоя 0,5 мм, у которой диэлектрическая проницаемость при переориентации молекул изменяется в пределах 2,7 - 3. Устройство настраивали на вторую полосу пропускания с тем, чтобы увеличить управляемый сдвиг фазы, а для уменьшения размеров конструкции в ее топологии проводников на подвешенной кварцевой подложке толщиной 0,3 мм использовали дополнительные скачки ширины. Рабочая полоса частот устройства составляла 5 ff =10 % и имела центральную частоту f =26 ГГц. После изготовления макета фазовращателя размеры топологии его проводников определяли на цифровом измерительном микроскопе, а затем именно эти размеры подставляли в программу анализа для объективного сравнения результатов расчета с экспериментом. На рис. 5 а представлены рассчитанные и измеренные амплитудно-частотные характеристики изготовленного макета, а на рис. 5 б показаны частотные зависимости управляемого сдвига фазы. Для переориентации молекул ЖК использовали внешнее магнитное поле напряженностью 3 кЭ, однако в этой же конструкции можно осуществить и электрическое управление фазой электромагнитных волн, если подавать напряжение смещения между микрополосковыми проводниками и корпусом устройства. На рис. 5 в показана фотография изготовленного макета фазовращателя.

Измеренная величина управляемого фазового сдвига в центре рабочей полосы частот составила 225°, что хорошо согласуется с величиной, вычисленной по полученной формуле (7) с учетом диэлектрических потерь ЖК. Видно не только достаточно хорошее согласие теории и – 190 –

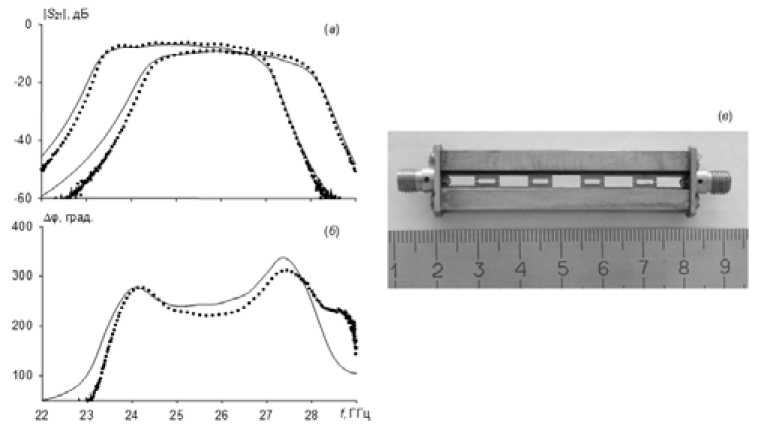
Рис. 5. Амплитудно-частотные характеристики ( а ), зависимость максимальной величины управляемого фазового сдвига от частоты ( б ) и фотография ( в ) исследованного фазовращателя (линии – расчет, точки – эксперимент)

эксперимента, но и сравнительно большой управляемый сдвиг фазы в устройстве при высокой степени его миниатюрности. Фактор качества устройства, определяемый как отношение максимальной величины управляемого фазового сдвига к средним потерям [4] и используемый для объективного сравнения различных конструкций фазовращателей, составил 30 град/дБ. Важно отметить, что характеристики имеющегося в наличии ЖК сравнительно невысоки – анизотропия диэлектрической проницаемости ∆ε=0,3 и тангенс угла диэлектрических потерь tgδ≈0,02. При использовании ЖК с лучшими характеристиками [6] в исследуемой конструкции можно получить существенно больший управляемый фазовый сдвиг при меньших потерях в рабочей полосе частот.

Заключение

В работе теоретически и экспериментально исследована конструкция микрополоскового электрически управляемого жидкокристаллического фазовращателя. Получено аналитическое выражение, связывающее величину управляемого фазового сдвига с основными конструктивными и электрическими параметрами фазовращателя. Проведенные исследования резонансной конструкции управляемого жидкокристаллического фазовращателя показали ее высокую эффективность и возможность использования в сантиметровом и миллиметровом диапазонах длин волн. Важной особенностью рассмотренной конструкции является то, что она также выполняет функцию полосно-пропускающего фильтра. В некоторых случаях это может значительно упростить схемы различных приборов, так как исключается необходимость использования в них дополнительных частотно-селективных устройств.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 гг.

Статья подготовлена и публикуется при поддержке Программы развития Сибирского федерального университета.