Исследование условий ликвидации неустойчивых однофазных коротких замыканий в линии с параллельными полуфазами 500 кВ

В [1] была обоснована схема дальней электропередачи СВН с использованием параллельных полуфаз. Как и в традиционных трехфазных линиях, в ВЛ с параллельными полуфазами целесообразно для ликвидации неустойчивых однофазных коротких замыканий применять однофазные автоматические повторные включения (ОАПВ). В многочисленных работах вопросы ОАПВ в традиционных трехфазных линиях проработаны основательно.

В частности, показано, что успешность ОАПВ определяется характеристиками вторичной дуги в длинных промежутках и эффективностью методов для снижения вторичного тока дуги (ВТД) и после гашения вторичной дуги восстанавливающегося напряжения (ВН).

Вторичная дуга подпитывается через емкостную и индуктивную связи поврежденной фазы со здоровыми фазами в паузу ОАПВ. При оснащении ВЛ 4-лучевыми шунтирующими реакторами отключенная фаза будет физически связана со здоровыми фазами через 4-лучевой ШР.

Гашение вторичной дуги определяется ВТД, протекающим в дуге до ее гашения ( I д ) и ВН, возникающим в месте вторичной дуги после ее гашения ( U_BH ).

В [2] показано, что среднее время гашения дуги зависит от установившегося ВТД. Зависимость допустимой длительности паузы ОАПВ представлена на рис. 1.

Необходимо также принимать во внимание степень загрузки линии и увеличение во время динамического перехода угла между напряжениями по концам линии, достигающего величин δ ≈ 2λ, где λ – электрическая длина линии.

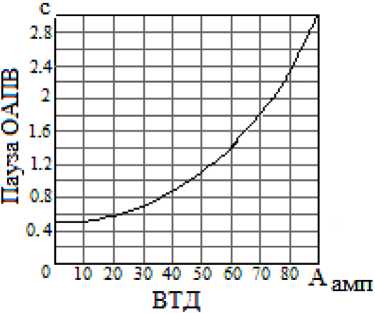
Рис. 1. Зависимость допустимой длительности паузы ОАПВ от амплитуды вынужденной составляющей ВТД

Fig. 1. Dependence of the permissible duration of the SPAR pause on the amplitude of the forced component of the SAC

При этом адекватное моделирование линии является необходимым условием для получения корректных результатов. В следующем разделе описана методика, использующая теорию многополюсников для надлежащего учета процессов в линии.

Анализ в данной статье выполнен для ВЛ 500 кВ с параллельными полуфазами (рис. 2), которая имеет следующие геометрические размеры: межфазовое расстояние по горизонтали и вертикали – 10 м; средняя высота подвеса нижних фаз – 11 м; расстояние между тросом и верхними фазами по вертикали – 6 м; конструкция фазы 3×АС-400; шаг расщепления – 0,4 м; конструкция троса – АС-70.

На рис. 3 приведена принципиальная схема ВЛ с параллельными полуфазами, применительно к которой рассматривается вопрос ликвидации неустойчивых ОКЗ в паузу ОАПВ.

Алгоритм расчета ВДТ и ВН в линии с ПП

Наиболее универсальным методом расчета является матричный метод, в котором линия и другие элементы электропередачи представляются в фазных координатах. Для получения общей картины достаточно оценить ВТД в узловых точках 1 и 2. На рис. 4 представлена схема

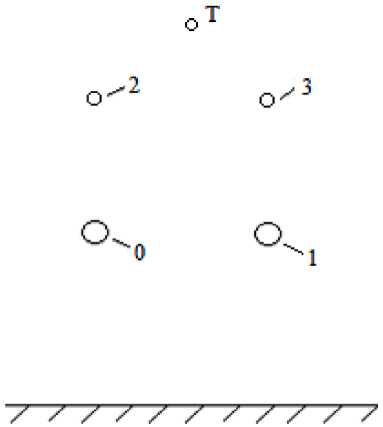
Рис. 2. Схема расположения фаз и полуфаз над землей

Fig. 2. Layout of phases and half phases above ground

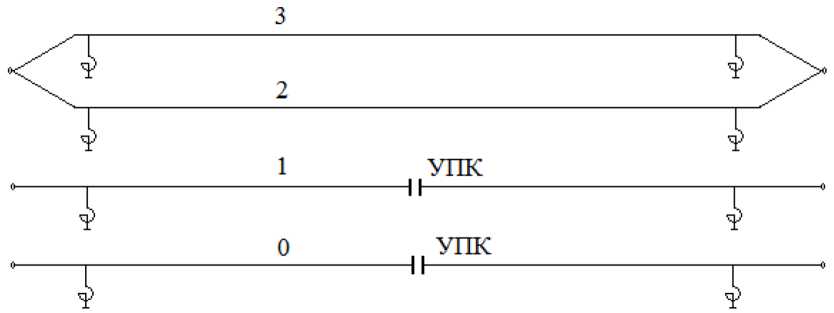
Рис. 3. Принципиальная схема ВЛ с параллельными полуфазами

Fig. 3. Schematic diagram of an overhead line with parallel half-phases

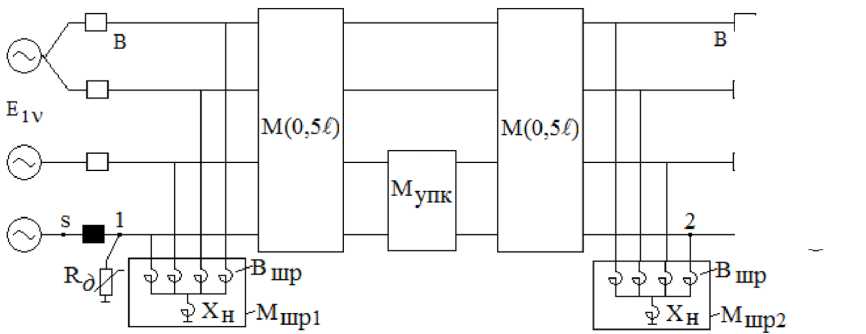
Рис. 4. Полная схема ВЛ с ПП для расчета ВДТ и ВН

Fig. 4. Complete diagram of overhead lines with PHPh for calculating SAC and TRV для расчета ВТД в начале линии в виде каскадного соединения отдельных участков, каждый из которых замещается соответствующим многополюсником (на рис. 4 ВТД обозначен как Iд).

Полная фазная матрица схемы формируется согласно рис. 4:

М$г=МвМдМшр1м^-5^Мупк -M^M^-Mg

Соответствующие матрицы в формуле (1) определяются следующим образом.

Полная матрица нетранспонированного половинного участка линии имеет вид

M(o,5l) =

А(о, si) В(о, si)

,

где

"4,o(o,5£) 41^0.50 4)2(0,5£) 4)з(0.50" 4o(oa£) 4i(<^1) 42(oa£) 4з(о,5£) A(0,50= v42O(o,5£) Л21(о,з£) Л22(о,з£) Л23(о,з1) _Лзо(о,з1) Л31(о,з1) Л32(о,з1) Л33(о,з1) Soo(o,sl) Sol(o,sl) SO2(o,sl) SO3(o,sl) Sw(0,5£) Sn(o,5l) S12(0,5£) S13(o,5£) B(0,50= 52O(o,5£) S21(o,5£) S22(o,5£) S23(o,5£) S3O(o,5£) S31(o,5£) S32(o,5£) S33(o,5£) Coo(o,5£) Co1(o,5£) CO2(o,5£) CO3(o,5£)" C1o(o,5£) Ch(o,5£) C12(o,5£) C13(o,5£) C(0,5l)= C2O(o,5£) C21(o,5£) C22(o,5£) C23(o,5£) QoCo.50 C31(o,5£) C32(o,5O C33(o.5O_ "Z)oo(o.5O D01(0.5f) DO2(o.5O D03^n Ao(oa£) Ai(oa£) A2(oa£) Аз(о,5£) D(0,5Q= Z)2O(o,5£) Z)21(o,5£) Z)22(o,5£) Z>23(o,5£) – матричные фазные коэффициенты _D3O(o,5O Z>31(0,50 D32(0.50 Z>33(0,50 для половинного участка линии.

Полная матрица шунтирующего реактора при наличии нулевого реактора в его нейтрали запишется как

м = tup где ¥ , = 7Г1 , где			14    04 V     1 *-шрф jXH	, jXH	jXH "
	^шр "*" j^H
	jXH	Хг	tip    J ri	jXH	jXH
^шрф	jXH		jXH	^lup "*" jXu	jXH
	jXH		jXH	jXH	^lup ^ jXy

где Zшр – фазное сопротивление собственно шунтирующего реактора; Xн – сопротивление ней- трального реактора.

Полная матрица УПК имеет вид

м =

упк

I4 ^упК

04   14

2упк    О О О упк

О    Х_упк о о

О  ООО

О  ООО где Zупк – фазное сопротивление УПК.

Нулевая и единичная матрицы 4-го порядка соответственно находятся как

	"0	0	0	0"	"1	0	0	0"
04 =	0 0	0 0	0 0	0 0 ’	0 *»= 0	1 0	0 1	0 0 '
	0	0	0	0	0	0	0	1
Рис. 5 показывает	схему		моделирования			коммутационного состояния выключателя

(В). Если R_v = 0, то это соответствует включенному состоянию фазы v . При R_v → ∞ будет моделироваться разомкнутое состояние. Для проводимого анализа достаточно принять Rv = 10⁶ Ом.

Соответственно, полная матрица состояния выключателя выглядит так:

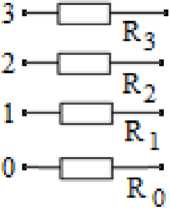
Рис. 5. Моделирование коммутационного состояния выключателя

Fig. 5. Modeling the switching state of a circuit breaker

Мв =

Re

14 ’

где

о о о

о

*1 о о

о

о

^2

о

о о о

R3

Например, для фазы ключена.

где

– матрица состояния выключателя.

о

о

о

о

о

о

о

о

0

О

О

о

о

о

о

106

Полная фазная матрица дуги имеет вид

,

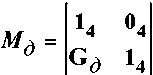
0, 1 и полуфаза 2 включены, а полуфаза 3 от-

о о о

о о о

о о о

о

о

о

о о о

– матрица дуги для полуфазы 3.

Rd

Проводимость дуги занимает соответствующее место на главной диагонали матрицы дуги в зависимости от фазы или полуфазы, на которой имеет место дуга.

ВТД зависит от сопротивления вторичной дуги, которое является нелинейной функцией ВТД. Принимая во внимание модель дуги, представленную в [3], сопротивление дуги можно аппроксимировать следующим выражением:

где для ВЛ 500 кВ а = 1,4 и А « 1,3 • 105.

Как показано в [4], для определения ВТД можно воспользоваться следующим нелинейным уравнением:

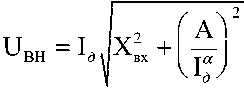
где UВН – ВН в месте возникновения дуги после ее погасания; XВХ – реактивная составляющая входного сопротивления пассивной электрической цепи со стороны места возникновения дуги при ее отсутствии.

Наиболее просто ВДТ определяется путем графического решения вышеприведенного нелинейного уравнения.

В целом алгоритм для определения ВТД строится следующим образом. Сначала определяется полная фазная матрица всей схемы согласно (1), а также полная фазная матрица участка 1-r.

Далее определяются соответствующие подматрицы этих полных матриц

A_sr = submatrix^M_sr , 0,3,0,3), B_sr = submatrix^M_sr , 0,3,4,7), A_lr = submatrix^My, 0,3,0,3), В = submatrix^M^, 0,3,4,7).

Определив вектор-столбец фазных токов в конце схемы

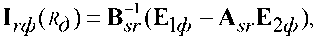
где

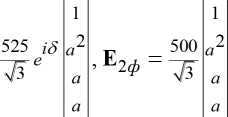
вектор – столбцы заданных ЭДС по концам линии,

Пл/ . /3

,

найдем вектор-столбец фазных напряжений в i-м узле в месте горения дуги:

и1ф(Rд) - A1 rЕ2ф + B1 rIrф(Rд).(11)

Далее определяется напряжение в месте горения вторичной дуги:

U(R д) = и1фз,о(R д).(12)

Заметим, что полагая в (12) Rv ^ да (практически достаточно принять Rv = 10 6 Ом), найдем из (12) ВН на аварийной фазе после гашения вторичной дуги:

UЗн = U(R д = 106).(13)

Входное сопротивление относительно места дуги определится как

XBX=Jm------вн----,(14)

:кз (Rd = 1 Ом)

ивн где                       – ток в месте дуги при ее шунтировании.

1кз(Кд=10м)

Анализ ВТД и ВН при ликвидации ОКЗ в концевых узлах полуфаз

Основываясь на предложенном алгоритме, проанализируем условия гашения вторичной дуги для ВЛ 500 кВ при возникновении аварий в концевых узлах схемы, где имеют место наиболее неблагоприятные условия. Реактивная мощность ШР на фазу составляет 60 Мвар.

Сначала рассмотрим необходимые условия, при которых гарантируется успешное ОАПВ. Длительность паузы успешного ОАПВ, не превышающая 1,0 с, удовлетворяется при условии

I

втд ≤ 45А

ампл .

Второе обстоятельство, которое должно приниматься в расчет, это создание приемлемых условий для работы защитных аппаратов ОПН, установленных на концах линии.

После гашения дуги имеет место реакция отключенной фазы, обусловленная взаимодействием емкостных и индуктивных элементов электропередачи. ВН имеет форму биений, поскольку свободная частота близка к промышленной частоте.

Как показано в [5], для ВЛ 500 кВ допустимая величина вынужденной составляющей ВН оценивается величиной Uвн.доп = 230 кВ, и, соответственно, должно выполняться условие

U вн ≤ U вн.доп .                                                                   (16)

На рис. 6 представлены результаты расчетов ВН в узле 1 при аварии в полуфазе 3 в зависимости от величины проводимости ШР, установленных на аварийной полуфазе 3 (ПФ3).

При номинальной проводимости ШР, равной В_{шр .н ом} = 6,53 ∙ 10^–4 См, имеют место резонансные условия. Для того чтобы обеспечить допустимый уровень ВН, требуется в режиме паузы ОАПВ снижение проводимости ШР, что может быть сделано при использовании управляемых ШР [6]. Более простое и эффективное решение состоит в отключении ШР2 на аварийной полуфазе ПФ3, что иллюстрирует рис. 7.

По данным табл. 1 на рис. 8 а и 8 б приведено графическое решение уравнения (8), результатом которого являются ВТД, приведенные в этой же таблице.

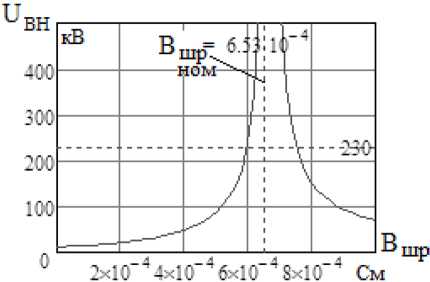
Рис. 6. Зависимость ВН в узле 1 от проводимости ШР на ПФ3

Fig. 6. Dependence of TRV at node 1 on the conductivity of the ShR at HPh3

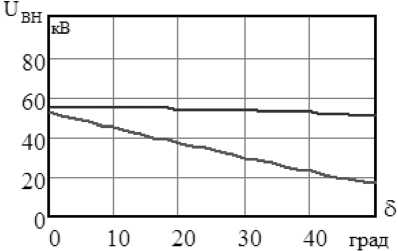
Рис. 7. Зависимость ВН в узлах 1 и 2 от углового сдвига на линии

Fig. 7. Dependence of TRV at nodes 1 and 2 on the angular displacement on the line

Таблица 1. Данные схемы и результаты решения уравнения (8) при ОАПВ ПФ3

Table 1. These schemes and the results of solving Eq. (8) at SPAR HPh3

Схемные и режимные параметры Анализируемый узел	UBH , кВ	XВХ, Ом	Iд, Аамп	t ОАПВ , с
Узел 1	51,8	1321	42,4	0,93
Узел 2	54	1440	42,4	0,93

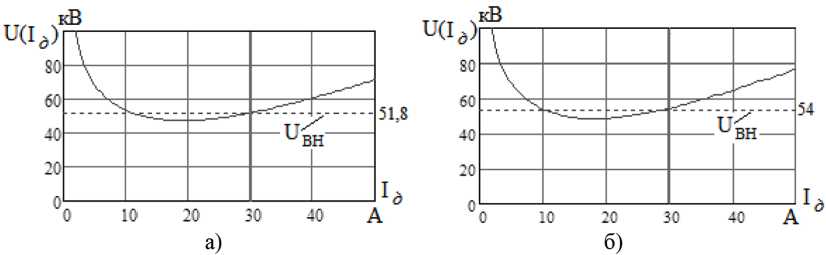
Рис. 8. Графическое определение ВТД: а – в начале линии; б – в конце линии

Fig. 8. Graphical definition of SAC: a – at the beginning of the line; б – at the end of the line

Как следует из табл. 1, условие (15) выполняется.

При осуществлении ОАПВ в случае аварии на полуфазе 2 результаты расчетов мало отличаются от предыдущего случая, если на аварийной ПФ2 отключается ШР1, что подтверждают данные табл. 2.

Особенность подпитки тока дуги при авариях на ПФ3 и ПФ2 состоит в том, что напряжения остающихся в работе Ф1 и Ф2 и полуфазы ПФ2 (или ПФ3) образуют симметричную тройку векторов, в результате чего ВТД имеют пониженный уровень. При авариях на Ф1 или Ф2 имеет место ситуация, сходная с традиционными трехфазными линиями, и поэтому в данных случаях задача снижения ВТД решается хорошо известным способом, а именно путем включения в нейтраль ШР нулевого реактора [7], что существенно снижает электростатическую составляющую тока подпитки.

На рис. 9 показана зависимость ВН от величины нейтрального реактора.

Наименьшие ВН имеют место при значении нулевого реактора в диапазоне Xн=400–600Ом.Вэтомслучаенапряжениена нейтралях ШРне превышает допустимыйуро-

Таблица 2. Данные схемы и результаты решения уравнения (8) при ОАПВ ПФ2

Table 2. These schemes and the results of solving Eq. (8) at SPAR HPh2

Схемные и режимные параметры Анализируемый узел	U BH , кВ	X ВХ , Ом	I д , Аамп	t ОАПВ , с
Узел 1	55,3	1440	43,8	0,96
Узел 2	53	1321	43.8	0,96

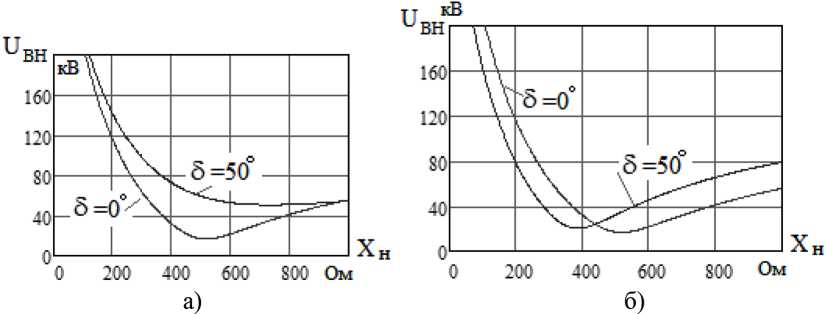
Рис. 9. ВН в зависимости от сопротивления нулевого реактора: а – в начале линии; б – в конце линии

• Fig. 9.    TRV depending on the resistance of the zero reactor: a – at the beginning of the line; б – at the end of the line

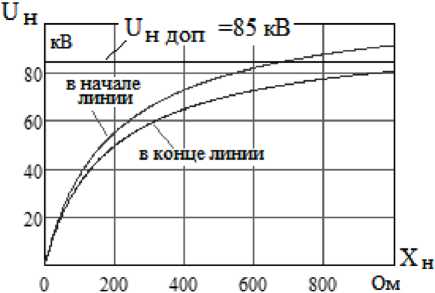
Рис. 10. Напряжение на нейтралях ШР в зависимости от сопротивления нулевого реактора

• Fig. 10.    Voltagejn the neutrals ShRdepending on the resistance of the zero reactor

Таблица 3. Данные схемы и результаты решения уравнения (8) при ОАПВ Ф1

Table 3. These schemes and the results of solving Eq. (8) at SPAR Ph2

Схемные и режимные параметры Анализируемый узел XHОм UBH, кВ XВХ, Ом Iд, Аамп tОАПВ, с Узел 1 400 72,8 2569 35,4 0,79 Узел 2 400 31,7 2569 0 0,5 вень, как это следует из рис. 10, который для изоляции класса 35 кВ, по данным [7], составляет 85кВ.

По данным табл. 3 на рис. 11 а и 11 б приведено графическое решение уравнения (8) для случая аварийной ситуации на фазе 1, результатом которого являются ВТД, приведенные в этой же таблице.

Как вытекает из данных табл. 3, условие (15) выполняется с большим запасом, при этом при аварии в конце линии ВН недостаточно для возникновения вторичной дуги.

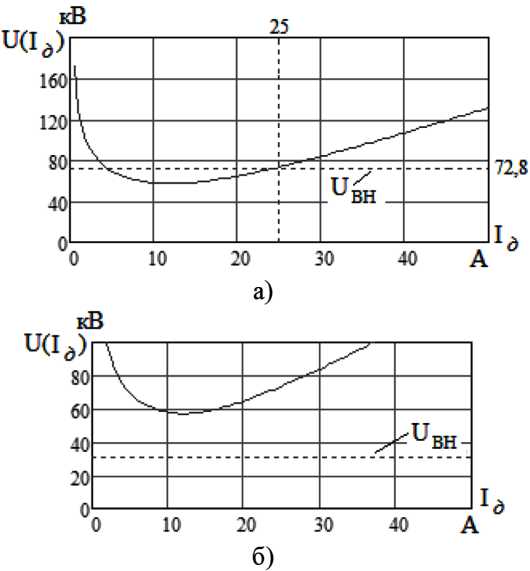
Рис. 11. Графическое определение ВТД при аварии на Ф1: а – в начале линии; б – в конце линии

Fig. 11. Graphical definition of SAC in case of accident on Ph1: a – at the beginning of the line; б – at the end of the line

Таблица 4. Данные схемы и результаты решения уравнения (8) при ОАПВ Ф0

Table 4. These schemes and the results of solving Eq. (8) at SPAR Ph0

Схемные и режимные параметры Анализируемый узел	XHОм	UBH , кВ	XВХ, Ом	Iд, Аамп	t ОАПВ , с
Узел 1	400	29,1	2569	0	0,5
Узел 2	400	70,1	2569	32,5	0,74

При осуществлении ОАПВ в случае аварии на фазе 0 результаты расчетов оказываются подобными предыдущему случаю, если используются нейтральные реакторы величиной 400 Ом, что подтверждают данные табл. 4.

Заключение

В данной статье обоснован метод для анализа ОАПВ в нетранспонированной линии 500 кВ с параллельными полуфазами. Предлагаемый алгоритм позволяет рассчитывать восстанавливающиеся напряжения (ВН) и вторичные токи дуги (ВТД) в концевых пунктах аварийных фаз и полуфаз, принимая в расчет реальное расположение фаз и полуфаз над землей.

В статье доказывается, что при ликвидации однофазных аварий на полуфазе 2 достаточно отключить ШР1 на аварийной ПФ2, а при аварии на полуфазе 3 следует отключить ШР2 на аварийной ПФ3. При ликвидации аварий, воникающих на рабочих фазах 0 и 1, требуется включение в нейтраль ШР1 и ШР2 нулевых реакторов с оптимальной величиной порядка 400 Ом.

В результате использования предложенных мероприятий обеспечивается успешное ОАПВ при бестоковой паузе в пределах 1,0 с.