Исследование устойчивости алгоритма восстановления фазы к отсутствующей информации в центре детектора в случае когерентного рассеяния на упорядоченной структуре

Когерентная рентгеновская дифракционная микроскопия (КРДМ) – универсальный и мощный метод рентгеновской микроскопии низкого разрешения, разработанный для визуализации некристаллических и упорядоченных образцов на нано- и микромасштабах [1–4]. Для восстановления комплексной волновой функции рассеянного излучения и дальнейшего получения изображения в реальном пространстве из интенсивности дифракции часто используется один из самых простых и эффективных алгоритмов – гибридный алгоритм ввода-вывода ( hybrid input-output , HIO), разработанный Финапом [5]. При восстановлении фазы при помощи HIO используется только измеренное двумерное распределение интенсивности дифракционной картины и приблизительная оценка формы и размеров образца [6]. Если форма и размеры образца неизвестны, но область когерентности рентгеновского пучка превышает размер образца как минимум в два раза, решение фазовой проблемы возможно при помощи алгоритма компактной свёртки, который позволяет последовательно восстановить форму образца из двумерной автокорреляционной функции (также известной как функция Паттерсона) [6].

Частой проблемой в экспериментах по КРДМ в трансмиссионной геометрии является отсутствие нескольких начальных гармоник дифракции в центре позиционно-чувствительного детектора (ПЧД). Это происходит из-за необходимости защиты центральных пикселей матрицы ПЧД от прямого пучка рентгеновского излучения. Отсутствующие Фурье-гармоники, закрытые бимстопом, значительно искажают восстановленное изображение в реальном про- странстве при итерационном восстановлении фазы в экспериментах по КРДМ, Брэгговской КРДМ и пти-хографии [7–10].

Несмотря на то, что проблема отсутствия информации из центральных пикселей была детально проанализирована в работах [7–9, 11], влияние тени от бимстопа в задаче КРДМ для упорядоченной структуры может заметно отличаться от примеров, рассмотренных в предыдущих исследованиях, благодаря изолированности значительной части интенсивности рассеяния в области дифракционных пиков. Эта частная задача актуальна, например, для исследования ансамблей самоорганизующихся объектов, наноструктур, топологических магнитных решёток и других упорядоченных систем.

Основная часть

Мы провели численное моделирование для оценки устойчивости HIO для восстановления фазы в эксперименте малоугловой КРДМ в трансмиссионной геометрии. Алгоритм HIO включает в себя параметр в для обратной связи между исходным изображением р ( r ) на основе желаемого изменения выходного изображения р '( r ):

_n [р ⁽ i ^{+ 1)}( r ), r ^G S ,

р ^{( 1 + 1)} ( r ) = <

[р( 1)(r) -вр( 1)(r), r 4 S, где S обозначает множество точек, где р(r) выходит за пределы, ограниченные краем образца и, следовательно, требует изменений.

В качестве оригинального изображения была выбрана микрофотография массива самоорганизованного монослоя магнитных наночастиц, снятая при помощи сканирующего электронного микроскопа (рис. 1a). Размер исходного изображения и его Фурье-образа составляет 650×650 пикселей. Изображению была придана несимметричная форма, состоящая из трёх пересекающихся кругов, для исключения эквивалентных решений и лучшей стабилизации алгоритма. В качестве входных данных HIO были использованы матрицы с абсолютным значением Фурье-образа исходного изображения с добавленным к нему шумом, по амплитуде сравнимым со структурными пиками второго порядка (~1/3 интенсивности пиков первого порядка, отношение сигнал/шум SNR=3,54), а также изображение формы объекта и параметр обратной связи β = 0,9. Мы не использовали критерии неотрицательности и вещественности возможных решений.

Алгоритм сходится к локальным минимумам после 200 итераций. После 100 индивидуальных попыток результирующие восстановленные изображения усреднялись. В первую очередь, исходное изображение было восстановлено из картины дифракции, не содержащей затенённых пикселей. Далее мы последовательно удаляли информацию из цента детектора в радиусах R = 10; 20; 30; 40; 50 пикселей (рис. 1 e ).

а)

г)

д)

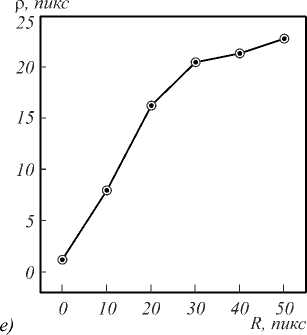
Рис. 1. Численное исследование эффективности алгоритма восстановления фазы HIO: исходное изображение

650×650 пикселей (а); изображения, восстановленные с помощью HIO из абсолютного значения Фурье-образа с отсутствующими начальными гармониками в центральном круге с радиусом R=0 (б); R=20 (в); R=50 пикселей (г); Фурье-образ исходного изображения (а) (пунктирными линиями обозначены границы круга с удаляемой информацией) (д);

функция разрешения в реальном пространстве в зависимости от радиуса круга R (е)

Ансамбль наночастиц на исходном изображении упакован в двумерную гексагональная решётку. Соответственно, Фурье-образ изображения содержит в себе следующую информацию: структурный фактор (набор из шести дифракционных пиков, симметрично расположенных вокруг центра детектора), формфактор каждой наночастицы и форм-фактор образца в целом. Форма пиков также является результатом интерференции структурного фактора рассеяния и форм-фактора образца, для восстановления которого из двумерной автокорреляционной функции достаточно одного такого пика [3,6].

В случае, когда все пиксели в центре Фурье-образа не затенены, исходное изображение восста- навливается полностью (рис. 1б). Кроме того, полное восстановление изображения возможно при удалении из центра картины круга с радиусом до 4 пикселей. При увеличении радиуса R информация о форме и размерах индивидуальных наночастиц и точном расположении дефектов теряется. В экстремальном случае, при удалении пикселей в окружности R =50 пикселей, то есть всей информации в пределах пиков первого порядка, частичное восстановление информации об объекте всё ещё возможно. Тип решётки и координаты частиц, за исключением дефектов упаковки, определяются с высокой точностью (рис. 1в, г). Качественно данный результат можно объяснить следующим образом. В кинематическом приближении амплитуда интенсивности когерентного рассеяния от упорядоченной структуры является свёрткой структурного фактора решётки, формфактора частиц (Фурье-образ единичного пятна) и форм-фактора апертуры (Фурье-образ формы объекта, в данном случае – асимметричной маски). В плоскости образца функция распределения электронной плотности для идеальной периодической структуры дана в виде v (r)= Σn δn (r – Rn), где Rn – координаты частиц в решётке. Фурье-образ этой функции ρ (q)= Σn δn (q – qn) определяет вектора обратной решётки qn и положения дифракционных пиков соответственно. Тогда амплитуда функции рассеяния Am выражается в следующем виде: A(q) = Σn Φ (qn) S (q) v (q)= Σn Φ (qn) S (q – qn), где Φ (qn) – форм-фактор одной частицы, S (q) – Фурье-образ формы образца. Таким образом, форм-фактор Φ (qn) только модулирует структурные пики и представлен только в некоторых точках Фурье пространства, определённых структурным фактором. Обратное Фурье-преобразование даже затенённой картины рассеяния возвращает координаты частиц в решётке, если она содержит дифракционные пики δ (q – qn). Пики модулируются высокочастотной функцией формы объекта в Фурье-пространстве S (q) и медленно меняющимся форм-фактором частиц – в нашем численном эксперименте средний размер частиц на изображении составляет 13 пикселей с разбросом

±6 пикселей, тогда как диаметр апертуры

330 пикселей. В симуляции использовалась область обратного пространства, включающая в себя только структурные пики первого порядка. Таким образом, для восстановления изображения формы частиц необходимо измерение структурных пиков высших порядков, модулированных форм-фактором. Можно заключить, что форма частиц, полученная на изображениях (рис. 1 в , г ), является не следствием формы реальных объектов, а пределом разрешения эксперимента. Данный эффект ранее наблюдался в эксперименте по КРДМ магнитных вихрей в тонкой пластине кирального магнетика [10] и наночастиц в фотонном кристалле [11 –13].

а)

б)

в)

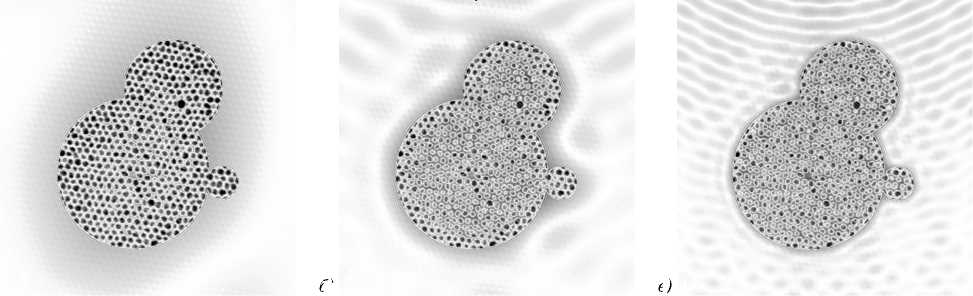
Рис. 2. Численное исследование чувствительности Фурье-голографии к затемненным пикселям в случаях R=0 (а); R=20 (б); R=50 пикселей (в)

Заключение

Данный результат показывает область применимости метода восстановления изображений в реаль-

Для подведения количественного анализа мы провели круговой корреляционный Фурье-анализ ( Fourier ring correlation , FRC) [14]. В данном случае FRC вычислялась как кросскорреляционная функция между исходным и восстановленными изображениями.

В качестве критерия отсечки FRC, определяющего разрешение для восстановленного изображения, было выбрано консервативное пороговое значение 1/2. Разрешение определяется точкой, в которой кросс-корреляционная функция необратимо пересекается с пороговым значением. В результате анализа функций FRC мы получили, что при увеличении радиуса тени бимстопа разрешения с 10 до 50 пикселей в обратном пространстве разрешение восстановленного изображения падает с ρ =8 до ρ =23 пикселей в реальном пространстве (рис. 1 е ). В данном случае значение ρ = 13 пикселей соответствует диаметру одной наночастицы на исходной картинке, то есть информация о свойствах индивидуальных объектов теряется уже при R = 10 пикселей. Тем не менее положение наночастиц в решётке определяется с высокой точностью даже в случае удаления всех пикселей между пиками первого порядка.

Для качественного сравнения подобный анализ был проведён для другого метода восстановления фазы – Фурье-голографии ( Fourier transform holography , FTH). В данном методе дифракционный волновой фронт модулируется известным опорным когерентным фоном, и картина в реальном пространстве восстанавливается единственным преобразованием Фурье [15]. В настоящем случае в качестве опорного фронта была использована окружность диаметром 5 пикселей, расположенная в 500 пикселях от центра изображения. Изображения, полученные в результате восстановления реального пространства в случаях затемнения 0, 20, 50 центральных пикселей дифракционной картины, представлены на рис. 2. При использовании данного метода разрешение восстановленного изображения не зависит от числа затемнённых пикселей, однако происходит неоднородная деформация контраста.

ном пространстве при помощи гибридного алгоритма ввода-вывода для экспериментов по когерентному малоугловому рассеянию и дифракции рентгеновско- го излучения. В случае использования бимстопа невозможно точное определение наличия дефектов упаковки и формы индивидуальных объектов, но возможно восстановление местоположений узлов упорядоченной решётки. Напротив, Фурье-голография устойчива к затемнённым пикселям в центре дифрак-тограммы. Как было показано в недавних работах по рентгеновской птихографии на оплоподобных наноструктурах [16, 17], данный метод тоже достаточно устойчив к наличию бимстопа.

Таким образом, для успешного восстановления фазы в задаче когерентной дифракции мы рекомендуем проводить несколько измерений с различными временами экспозиции для включения центральной области детектора в массив входных данных. Альтернативным решением может быть искусственная замена центральной области дифракционной картины на Фурье-образ известной формы объекта или использование опорной волны для восстановления фазы.

Работа выполнена при поддержке Швейцарского национального фонда научных исследований SNF Sinergia CRSII5-171003 NanoSkyrmionics.