Исследование устойчивости дислокационной подсистемы дисперсно-упрочненных материалов в условиях различных деформирующих воздействий

The model of dislocation subsystem evolution in heterophase alloys, containing noncoherent particles, is considered. The qualitative research of the dynamic system and the parametrical analysis are carried. The dislocation subsystem stability at various intensity of deformed effects is investigated. Availability of two stationary values of dislocation density is shown: steady p.'^!) and unstable p/²< At pF¹ < p < p,'^2-1 the dislocation density decreases when deformation increases.

Пластическая деформация кристаллов осуществляется преимущественно посредством локальных сдвигов в ограниченных областях кристаллографических плоскостей [1]. Каждая такая область (зона сдвига) возникает в результате испускания серии дислокационных петель после потери устойчивости дислокационным сегментом-источником. Каждая дислокационная петля в процессе ее формирования и расширения пересекается с десятками тысяч дислокаций некомпланарных систем скольжения (дислокаций "леса") [2,3]. Приблизительно, половина этих дислокаций оставляет ступеньки (пороги) на скользящих дислокациях. Движение порогов вместе со скользящей дислокацией сопровождается генерацией точечных дефектов - межузельных атомов и вакансий [1] При этом интенсивность генерации точечных дефектов тем выше, чем больше скорость дислокаций и, следовательно, чем выше их кинетическая энергия [3]

В области температур, где точечные дефекты достаточно подвижны, они достигают в процессе диффузионного движения дислокаций и аннигилируют на них При этом площадь экстраплоскости дислокации, являющейся стоком для точечных дефектов, уменьшается (при осаждении на дислокации вакансий) или возрастает (при осаждении межузельных атомов) При этом дислокации совершают диффузионные перемещения, которые сопровождаются аннигиляцией дислокаций при полном растворении экстраплоскостей или при их слиянии. Плотность дислокаций в кристалле в процессе его деформации может возрастать, уменьшаться или оставаться постоянной в зависимости от соотношения между интенсивностями генерации и аннигиляции дислокаций.

Проведено исследование устойчивости дислокационной подсистемы в дисперсно-упрочненных сплавах, в которых накопление дислокаций происходит кроме дислокационных барьеров (статистически накопленные дислокации [4]), также и на частицах второй фазы (геометрически необходимые дислокации [4]). Кроме того, значительный вклад в плотность дислокаций вносят дислокационные дипольные конфигурации [5]. Интенсивность генерации дислокаций в процессе пластической деформации может быть представлена, следовательно, как сумма трех слагаемых [6]:

+                                      (1

W ^^рь хръ

Первое слагаемое соответствует накоплению дислокаций на дислокационных барьерах, второе - вблизи частиц [5,6], третье - в дипольных конфигурациях, соединяющих частицы [5,6]. В (1) р - плотность дислокаций, b - вектор Бюргерса, Л - расстояние между частицами, D - диаметр зоны сдвига, F - безразмерный параметр [2], < х > - средняя величина параметра, характеризующего геометрию дислокаций, накопленных на частицах (призматических петель, колец Орована, петель вторичного скольжения), 8 - диаметр частицы.

Для области низких температур, где достаточно высокой подвижностью обладают только межузельные атомы, ограничимся рассмотрением аннигиляции дислокаций в результате осаждения на них деформационных точечных дефектов именно этого типа. Тогда для интенсивности аннигиляции дислокаций можно записать [6]:

К 7    3G^

где G - модуль сдвига, тауп=т-тк(р) - напряжение, избыточное над статическим сопротивлением движению дислокаций tr, т - приложенное напряжение. Такая ситуация может быть реализована при интенсивных деформирующих воздействиях, например, в камере Бриджмена, в шаровых мельницах и аттриторах, при интенсивных импульсных нагружениях.

Для условий динамического нагружения можно принять [3,5,6] F^l и DF2A где 1 ^ - длина пробега винтовой дислокации, равная [3,5,6]:

" ^p

Здесь < ДЕ,, > - средняя энергия образования деформационного точечного дефекта, р - доля порогообразующих дислокаций леса, £=0,5 - фактор Смоллмена.

С учетом (1)-(3), интенсивность накопления дислокаций в деформируемом дисперсно-упрочненном материале может быть записана [6]:

^dP ₌ ^FPA^<№k >   ₊ <Х>5 __1__ ^IWL п2

da %Tdynb3 Р 2X2pb \pb 3Gb V

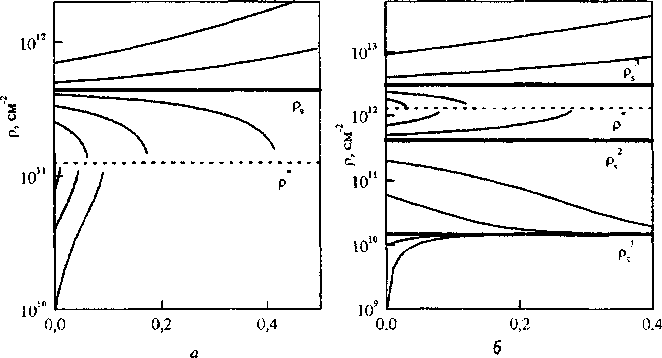
Уравнение (4) имеет два стационарных значения при р = р^ и р = р)²⁾, анализ которых показал, что возможны три случая. В первом случае, при низких значениях^,,, оба значения стационарных плотностей дислокаций р^, р<²⁾ являются комплексными и стационарные состояния дислокационной подсистемы отсутствуют (рис. 1,а). В этом случае при любых имеющих физический смысл значениях параметров модели и при любых начальных значениях ро плотность дислокаций в процессе деформации возрастает. Физически это может быть связано с двумя причинами 1) с уменьшением снижается интенсивность производства точечных дефектов дислокациями, так как замедление быстрых дислокаций, а затем их иммобилизация происходит при меньших линейных плотностях порогов; 2) уменьшается пробег дислокаций U , поэтому осуществление той же деформации связано с генерацией большей плотности дислокаций.

Во втором случае, при высоких значениях x_dyn оба корня являются действительными и различными (рис. 1,в). Стационарное состояние, характеризуемое плотностью р^, устойчиво, р⁽²⁾ соответствует неустойчивому равновесию.

Заметим, что возрастание плотности дислокаций при р>р*2) в рамках рассматриваемой модели ничем не ограничено (рис. 1). Это дает основание предполагать, что в кристалле в процессе деформации в таком режиме могут быть достигнуты плотности дислокаций, несовместимые с кристаллическим состоянием (р >1014 см"")

При плотностях дислокаций, близких к р®, вследствие неоднородности дислокационной подсистемы плотность дислокаций в локальных областях может быть выше или ниже стационарной величины. В областях, где р <р^2), плотность дислокаций будет монотонно уменьшаться, асимптотически приближаясь к стационарному значению р)”, соответствующему устойчивому равновесию. В областях, где р>р^2), будет происходить неограниченное возрастание плотности дислокаций пока существует кристаллическая решетка. Дислокационная подсистема распадается на две “фазы” с различной плотностью дислокаций. Вместе с тем, гетерофазный материал “распадается” на области кристаллического состояния и области аморфоподобного состояния

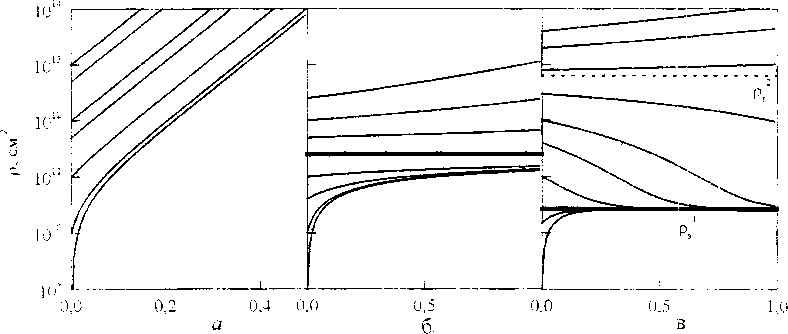
Рис. 1. Зависимость плотности дислокаций р от деформации при Лр=7-10"' см, G-10'МПа, Л’=2, ц*=2, 8=5-10"6 см и значения Тат(МПа) равны: а-100; 6-612. в-1000            ' '      ’

При некотором значении т.1уп стационарные значения плотностей дислокаций совпадают, pV'=P(,2)=Ps (Рис L6). При совпадении р^ и р^2) заключенная между шг ми область, в которой плотность дислокаций монотонно уменьшается с деформацией, исчезает. При плотностях дислокаций р<р, интенсивность накопления дислокаций dp/da >0, и плотность дислокаций асимптотически приближается к стационарному значению. При плотностях дислокаций р>р. интенсивность накопления дислокаций dpi da также положительна, но плотность дислокаций возрастает неограниченно. В гетерофазном материале со средней плотностью дислокаций р » ps в локальных областях, где р >р(, с увеличением деформации будет происходить нарастание плотностей дислокаций вплоть до достижения состояний,близких к аморфным. При этом дислокационная подсистема дисперсно-упрочненного материала ведет себя асимметрично по отношению к флуктуациям плотности дислокаций разного знака При локальных уменьшениях плотности дислокаций флуктуации “рассасываются”, и дислокационная подсистема возвращается в стационарное состояние, тогда как при отклонениях плотности дислокаций в сторону увеличения дислокационная подсистема неограниченно удаляется от стационарного состояния. Поэтому возникновение каждой флуктуации с р>р, сопровождается появлением новой высокодефектной области. С ростом дефор- мации число таких областей постоянно возрастает.

Таким образом, в зависимости от соотношения между плотностью дислокаций и избыточным напряжением кинетика дислокационной подсистемы может иметь существенно различный характер (см. рис. 1).

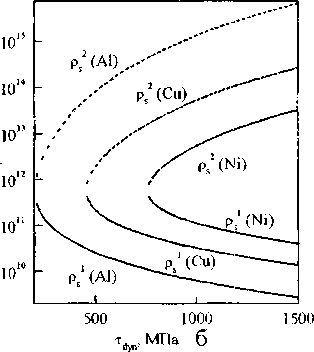
в -М10'4 см

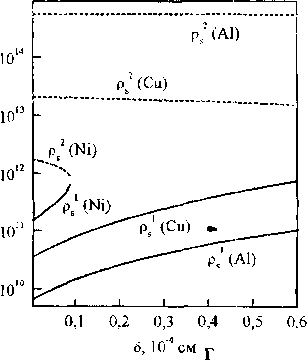
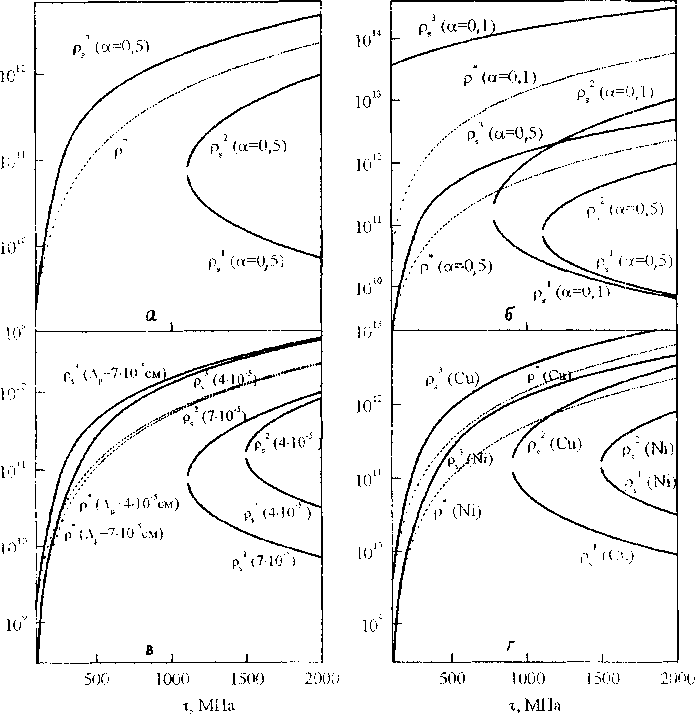
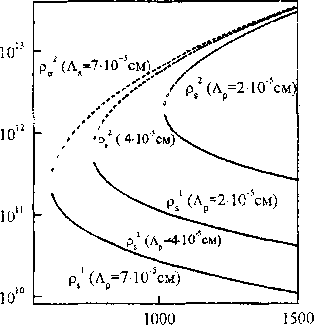
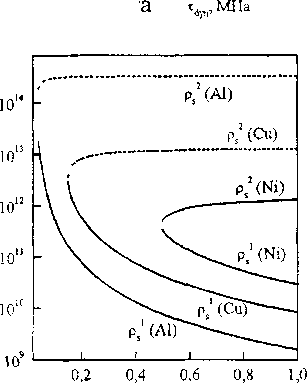
Рис 2 Стационарные значения плотности дислокаций при п*=2, 5=5-10"⁶см, G=2,710⁴ МПа (Al), G=610⁴ МПа (Си), G=10⁵ МПа (Ni) и a) G=10⁵ МПа; 6) Л_р=410'⁵ см, в) Td_yn=700 МПа, г) та_уп=8ОО МПа, Л_р=410"⁵см; ---- неустойчивое стационарное состояние;

--устойчивое стационарное состояние

На рис. 2 представлены диаграммы стационарных решений, на которых видно, в какой области значений параметров существуют два стационарных состояния, а также как изменяются значения стационарных плотностей дислокаций в зависимости от значений параметров модели, характерных для дисперсно-упрочненных материалов на основе никеля, меди и алюминия. Область значений исходной плотности дислокаций, при которой наблюдается деформационное разупрочнение с увеличением xdyn, расширяется. При некотором значении %d, определенном для каждого конкретного набора значений параметров, характеризующих дисперсно-упрочненный материал, как уже отме- чалось выше, оба стационарных значения плотности дислокаций - устойчивое и неустойчивое - совпадают, то есть область динамического разупрочнения отсутствует. Аналогичный характер изменения стационарных значений плотности дислокаций наблюдается с увеличением расстояния между частицами (рис. 2,в). С увеличением размера частиц 5 область значений исходной плотности дислокаций, при которой наблюдается деформационное разупрочнение, сужается (рис. 2,г).

Сравнение полученных результатов с результатами исследований моно- и поликристаллов однофазных материалов показывает, что общий характер поведения дислокационной подсистемы в поликристаллах однофазных материалов [7] и гетерофазных материалов аналогичен. И для тех, и для других наблюдается два стационарных состояния с аналогичным изменением параметрического портрета при изменении г^, что является, по-видимому, следствием того, что как в поликристаллах однофазных материалов, так и в гетерофазных материалах возникают дополнительные бартеры при движении дислокаций.

В сравнении с монокристаллами однофазных материалов в закономерностях изменения дислокационной подсистемы в гетерофазных материалах наблюдаются существенные различия: в однофазных материалах существует одно ненулевое стационарное состояние, в гетерофазных материалах их два [8].

Параметр тЛп весьма удобен при моделировании кинетики пластической деформации. поскольку он позволяет выделить динамические аспекты деформационного структурообразования. Однако для экспериментатора, который хотел бы исследовать закономерности пластического поведения материала в области деформационного разупрочнения, или для технолога, который хотел бы этими закономерностями воспользоваться, параметр т^, недоступен. Поэтому проведем исследование дислокационной подсистемы гетерофазных сплавов, деформируемых в условиях: 1) постоянной величины приложенного напряжения сдвига т; 2) постоянной нагрузки при одноосном растяжении и сжатии.

Рассмотрим поведение дислокационной подсистемы дисперсно-упрочненного материала при деформации с постоянным напряжением сдвига т. Если предположить, что деформация осуществляется под действием напряжения т»тк, то величину избыточного напряжения в этом случае можно представить в виде

Gb

U„=T~T--т-Ь -ссОйр А                 (5)

Исследование уравнения (4) в этом случае показало, что в зависимости от значений параметров модели существует одно или три стационарных решения. При этом существует особая точка р*=(т-т^ -СЬ/\Д_р - б)) /(a.Gb) , в которой нет решения

Исследование стационарных решений и р* показало, что возможны два случая:

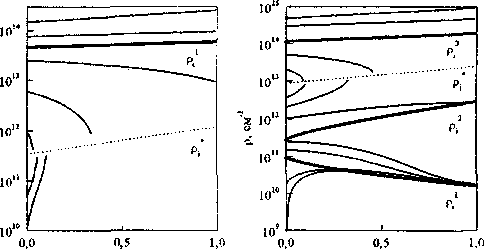
• 1)    Существует одно стационарное решение p_s, значение плотности дислокаций в котором выше значения плотности дислокаций в особой точке р*. В этом случае фазовое пространство (а, р) можно разделить на три области (рис. 3,а): первая, при р<р* интенсивность накопления дислокаций (/р/ da >0, и в этой области плотность дислокаций монотонно возрастает до значений р*. Вторая область, p*

  s, интенсивность накопления дислокаций

  dp! da<0, и в этом случае плотность дислокаций монотонно убывает до значений р*. При р>р$, что имеет место в третьей области, с увеличением деформации будет происходить нарастание плотности дислокаций. Таким образом, стационарное решение p_s является неустойчивым. Заметим, что возрастание плотности дислокаций при p>p_s в рамках рассматриваемой модели не ограничено.

• 2)    Существуют три стационарных решения p_s\ p_s², p_s³; в этом случае фазовое

пространство (а, р) можно разделить на пять областей (рис. 3,6). Первая, при р<р₅' интенсивность накопления дислокаций dpida>0, и в этой области плотность дислокаций монотонно возрастает до значений рД Вторая область, p_s^]

s², интенсивность накопления дислокаций

dp / da <0, и в этом случае плотность дислокаций монотонно убывает до значений Ps¹. И, следовательно, стационарное состояние, характеризуемое плотностью дислокаций рД, устойчиво. Третья область, p_s²

dp!da>0, и плотность дислокаций монотонно возрастает до значений р*. Четвертая область, р*<р<рД интенсивность накопления дислокаций dp!da и плотность дислокаций монотонно убывает до значения р*. Пятая область, р<р₅³, с увеличением деформации будет происходить нарастание плотностей дислокаций. Таким образом, состояния, характеризуемые стационарными значениями плотностей дислокаций р Д и рД, соответствуют неустойчивому равновесию (рис. 3).

Рис. 3. Зависимость плотности дислокаций р от деформации при Лр=7-10"5 см, G=105 МПа, F=2, п*=2, 5=5-10"6 см, т#=10 МПа, а=0,5 и т (МПа): а) 500; б) 1500

На рис. 4. представлены диаграммы стационарных решений для модели дисперсно-упрочненного материала, деформируемого в условиях постоянного напряжения сдвига т. При наборе значений параметров модели, характерных для гетерофазного материала на основе Ni, три стационарных решения появляются при высоких значениях напряжения, при этом с ростом т область деформационного разупрочнения расширяется (рис. 4,а). Параметрическое исследование модели показало следующие закономерности С уменьшением а три стационарных состояния дислокационной подсистемы появляются при меньших значениях т (рис. 4,6). Такая же зависимость наблюдается с увеличением расстояния между частицами (рис. 4,в), при больших значениях Лр три стационарных состояния появляются при меньшем напряжении, при этом уменьшается значение плотности дислокаций ps!, соответствующее устойчивому стационарному состоянию. На рис. 4,г приведены значения стационарных состояний для дисперсно-упрочненных материалов на основе меди и никеля.

Отметим, что при высоких значениях напряжения т, когда г » GZ>/(л^-б)+Ту +aGZip1 2, характер развития дефектной структуры, практически, аналогичен наблюдаемому в случае, рассмотренном выше при постоянном избыточном напряжении Tdvn, так как в области «реальных» значений плотности дислокаций будут наблюдаться два стационарных состояния, значение третьего стационарного состояния и особой точки р* превышают 1013 cm"z.

Рис. 4. Стационарные значения плотности дислокаций при F=2, м*=2.

5=5-10"6 см, тг=10 МПа и a) G=105 МПа, а=0,5, Лр=7-10"5 см,

б) G=105 МПа, Лр=7' 10"5 см, в) GH03 МПа, а=0,5, г) а=0,5, Лр=410"5 см, Си - G=6J04 МПа, Ni - GIO5 МПа. Обозначения: ps‘, ps2, ps3 -стационарные плотности дислокаций, р - особая точка

Было также проведено исследование модели для условий деформации при постоянной нагрузке (/^const). В условиях одноосного растяжения цилиндрического образца при постоянной нагрузке напряжение возрастает с изменением поперечного сечения образца в процессе деформации как т = т₀ехр(а/ к), где к - множитель Закса, в дальнейших расчетах принимаем км2.

Для выявления основных тенденций развития дислокационной подсистемы гетерофазного материала при P=const были найдены изоклины нуля для уравнения (4), то есть кривые, в каждой точке которых dpida-F Точки указанных кривых могут оказаться для интегральных кривых точками максимума и минимума. Изоклины нуля разбивают фазовое пространство на области, в которых производная имеет разные знаки, и. следовательно, поведение интегральных кривых р(а) имеет аналогичный характер.

Параметрическое исследование показало, что важным управляющим параметром при таком виде деформации является напряжение То. На рис. 5 приведены два возможных варианта развития дислокационной подсистемы в зависимости от значений То. Первый - когда дифференциальное уравнение имеет одну изоклину нуля pi1 и одну «особую» изоклину, при которой знаменатель обращается в нуль pi (рис. 5,а). Второй - дифференциальное уравнение имеет три изоклины нуля р/, рД р3 и «особую» изоклину pi* (рис. 5,6).

Рис 5. Зависимость плотности дислокаций р от деформации при а=0,1 и то (МПа): а)200; б) 800 (значения остальных параметров, как на рис. 3),. pi1, р;2, pi3 - изоклины нуля, pi - особая изоклина

Для одноосного сжатия число изоклин нуля в зависимости от значений параметров также одно или три. Однако зависимость изоклин от деформации при одноосном сжатии и растяжении имеет разный характер, а именно, с увеличением деформации при сжатии значение первой изоклины р^ возрастает, при растяжении - уменьшается. Значение других изоклин р;, pi2 и р;3 с ростом деформации уменьшается при сжатии, и увеличивается при растяжении. При этом область динамического разупрочнения между р/ и pi2 сужается с ростом деформации при сжатии и расширяется при растяжении

Проведенный анализ позволяет предполагать, что в зависимости от характеристик материала и его исходной дефектности возможно так подобрать деформирующее напряжение т, чтобы добиться желаемого режима деформирования.