Исследование устойчивости пластин с дефектами типа круглых отслоений
Автор: Бохоева Л.А.
Журнал: Вестник Бурятского государственного университета. Философия @vestnik-bsu
Рубрика: Физика и техника
Статья в выпуске: 6, 2007 года.
Бесплатный доступ
В данной работе рассматривается задача о нелинейном поведении пластины с круглым отслоением из слоистых материалов при потере устойчивости «смешанного» типа. Получены в явном виде характеристические уравнения для определения критической нагрузки пластины с дефектами типа отслоений в элементах конструкций, при одновременно локальной и глобальной потери устойчивости.
Короткий адрес: https://sciup.org/148178196
IDR: 148178196
Текст научной статьи Исследование устойчивости пластин с дефектами типа круглых отслоений
In the paper presents an nonlinear analysis of a plate with circular delamination from layered materials. The characteristic equations for definition of critical loading of a plate with defects of type circular delamination in elements of designs are received in an obvious kind, at simultaneously local and global loss of stability.
При проектировании конструкций из слоистых композиционных материалов весьма важной задачей является задача прогнозирования поведения их под нагрузкой. Дефекты типа отслоения являются распространённым видом дефекта и часто считаются определяющим фактором при решении вопроса об использовании композиционных материалов. В зависимости от относительных величин толщины и длины отслоения под действием сжимающих нагрузок наблюдаются три вида потери устойчивости элементов конструкций: общая потеря устойчивости (глобальная); локальная потеря устойчивости в зоне дефекта; одновременно локальная и глобальная («смешанная»).
Для длинных отслоений деформирование начинается с локального выпучивания тонкого отслоившегося слоя, но при увеличении нагрузки изгибные деформации возникают и в остальных частях элемента конструкции. В данной работе рассматривается задача о нелинейном поведении пластины с круглым отслоением при потере устойчивости «смешанного» типа. Из анализа существующих подходов для решения этой задачи следует, что метод математически либо строг и слишком сложен, либо предполагает проведение трудоемких вычислений. Поэтому назрела необходимость по лучения приближенного расчета закрити-ческих деформаций, которые предшествуют распространению дефекта, удобного для практического использования инженерам-конструкторам.
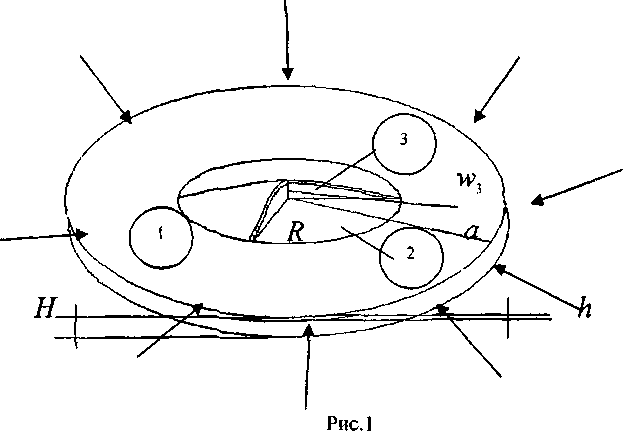
В работе рассматривается упрощенная конфигурация круглой пластины с радиусом а, которая имеет дефект в виде круглой платины с радиусом R, причем для нее выполняются следующие предположения:
-
1) Существует единственное приповерхностное отслоение круглой формы;
-
2) Это отслоение отделяет тонкий изотропный слой толщиной h от основной платины толщиной Н;
-
3) Размеры дефекта R малы по сравнению с основной пластиной, но велики по сравнению с толщиной отслоившегося слоя h,
В области дефекта пластина состоит из двух частей: отслоившаяся часть (верхняя) толщиной
h
с изменением радиуса 0 < г <
R
и нижняя часть, расположенная ниже отслоения, толщина которого равна
(H-h)
с изменением радиуса
0
г - h _ R с = —; h^ — ; а^ — ,
R Н а где и,(г) - радиальное перемещение, тДг)-функция поперечного прогиба, (1=1,2),
-
1 Работа выполнена в рамках целевой программы МОиН РФ «Развитие научного потенциала высшей школы (2006-2008 гг.)» (проект№ РНП.2.1.2.5517).
w,(r) и и^г)- функции перемещений, полученные в работе [1]. Пусть fj(r), Р2(г),
Р^г) соответственно нагрузка на 1,2,3 участках. Введем обозначения:
Q^=Pi^R. (i = l,3\ A2=Q,=^-, " D, 2 D2
hr^X-p)
(0<^ ^(г) = *, (f), W2(r) = w2(f) , W,(5-) = w2(r), „ EH1 где Dt =------— 12(1-Д2) 1 12(1-^) л ^-ш-. 2 12(1-A2)’ Рассмотрим второй участок. В полярной системе координат основное линеаризованное уравнение для круглой пластины, нагруженной контурными усилиями Рг, принимает вид = -л2^;(^), (о<^ <1). L J Не обращающееся в бесконечность при г-О решение для сплошной пластины как при осесимметричной, так и при неосесимметричной форме потери устойчивости определяется зависимостью wI(r) = SlJ0(^) + B2, где JtiAA ~ функция Бесселя, первого ро да J^) = -™J^). Следовательно, ^L^(r) = 4BA/R)J^). dr i R При r=R зависимость между перемещениями на 2 и 3 участках имеет вид ВЛ^Р V6(1-/22)^W" Так как при осесимметричной форме потери устойчивости напряжения и деформа ции на 2 участке равны Рг ^о-а) <7 = <7 =-----,Б = Ей =--- , то г ° (H-h) г ° E(H-h) величина радикального перемещения при r=R J О'ЯЖ При r=R прогиб дефекта (3 участок) и дефектного участка (2 участок) должны быть геометрически совместимы, т.е. должно быть выполнено необходимое условие совместимости Иэ(Я)=«2(/?)+уА(Я). Используя зависимости (1) и (2), имеем о-ц)ЕХгЕф-hf Е1,Н-h)UR4\- мА W(D = -«з(^) +----/ 2р4ьо-мА Отсюда следует выражение для Л2 ^=_J2^) (H-hf 3 Hh /6(1+/О ‘ +------Г ■ ■ —Wl) ПЕЕ<У^Л2 V 6(1 + /z) ни уанз+л I \-ц , Hh V«a+^( У На первом участке дифференциальное уравнение будет иметь вид: R J г , г I R = -Q №^), 1 <^ < —. R Введем обозначение функции/(<;) тогда уравнение (5) имеет вид АД - ц)В2 + ВД + = _Д-нигВ2 + Н - h , h2E i 1-/2 (H-hf; 2Уб(Ь^5 У 6(1 + ^ НИ . h2E пкд-^ 2^6(1-/?) Hh ^6Д + д) 3 тогда дифференциальное уравнение можно представить в виде Д-^и2Р2 hE(H - Hf H-h + 2-6(H-h)H VO-^Xi + ^Xi + A) ^-a^w), а R' 12Д£А [Д7^)Д7^)(Р7Д 127/ \Д + ^Д-а)Д + ^) приr=R /(1) = ^(1). Первый участок можно представить в виде толстостенной трубы, находящейся под действием внешнего давления, тогда (1-/z)22D2(1 (Я-й) + REhu3(R) - напряжения и перемещения равны <тДг>А-Вг"2; crff(r) = А + Вг~2; wi(r) = T Е АД-рУ + ВД+у)-г Уравнение совместимости второго и первого участков при r=R, полученное из условия укорочения под действием сжимающей нагрузки и дополнительного сближения вызванного изгибом дефекта, можно записать в виде: иДВ^иДВ^™1^. (4) С учетом уравнений (1), (2), (3) уравнение (4) преобразуем следующим образом Л(1-//)Я2+£(! + //) = = _ (I^aH^+^(1) , (5) (Н - А) 2^Д-мЪ где PJC = Л^,. Так как функцию ^(1) можно представить в виде = (1-//)Л2£>2 — + REhu3(R) Н Сделав преобразования, получаем Д]-//)/?2 + 5(1 + //) = ^-Х-^ХгО2+КЕЬиДВ^ ^ В сечении на границе дефекта должно выполняться уравнение равновесия сил (при z=R\. Рг-Рг+Рз, Д ^ ' 2" R1 ’ R1 или R2 R2 R2 Так как при r=R имеет место следующая зависимость о- / „ = A-B!R2 =--^~, тогда г r-к нг A-В/R2 =Ч6зД)ПлА2ОД/НР2. Решая совместно систему уравнений (4), (6), при г - R можно найти коэффициенты А и В, которые равны 5=11й№ 2 [ Н + REhu3 (7?) А= 2^"й№ "^ + ^^ ' Так как ' Н HR2 г2 тогда ^ц <40 ^ R R^-X) -AHR? BHR1 D/ На втором участке при r = R -^^^^"Т^ + ^W] + +^^[£№+^3w]= + 0-Л? X * REhuXRy — Л “И k ; ЖХ ) При r=R величина Q. (^) равна a^^^aoL^]. М^ - D^ NW R^^AV^h Радиальное перемещение при rR равно МЛ) = | А(\-^a+B(\ +^~ NW ^2^^ + ^ ^0) _ тг27бО-?) J^ R R^N^i?) r2J6 На третьем участке: M3(.R) = = -, ,Д-^ -[>/’(1)+U + Dv'(l)]. Из уравнения равновесия моментов получаем выражение для вычисления/^ при ^ -1, т.е. при r^R , Уh , [/'(1) + ^чу(1)]= К’АбХХ-м’Х 2EHR1 х[-£ (1) D3 - 2АгПг + REhu3 (/?)] + +^[аО)с>+№,№]■ (s) При заданных геометрических параметрах и характеристиках материала по формулам (7) и (8) можно определить критическую нагрузку и перемещения круглой пластины с дефектом. Уравнение равновесия моментов имеет вид мук^мда* +—-^=^==[^’(1) + (1 + //WD] + А24б.(1-А2) Jvh Pv где;2—r2 - r2 , сделав преобразования, окончательно получаем: /'(l) = -/zy/(l) + +M3(R) + ^-^—^ 3 2 2 При r-R на первом участке +/i3[V(l)-f-(l + /z)^(l)] + + ----------X X я2-(]-д)3-л2(1-й).д3(1) В работе получены в явном виде характеристические уравнения для определения критической нагрузки и закритического поведения пластины с дефектами типа круглых отслоений в элементах конструкций из слоистых материалов, при одновременно локальной и глобальной потере устойчивости.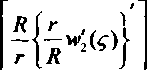
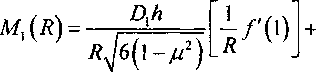
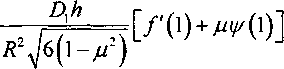
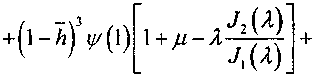
Список литературы Исследование устойчивости пластин с дефектами типа круглых отслоений
- Бохоева Л.А. Устойчивость круглых отслоений в слоистых элементах конструкций с учетом поперечного сдвига//Межвуз. сборник науч. трудов. -Чита, 1994. -С. 21-25.


