Исследование устойчивости пологих панелей из гибридных материалов с разрушающимися слоями композита

Гибридные композиционные материалы представляют собой сочетание нескольких типов армирующих наполнителей с различными упругими и прочностными свойствами в одной матрице. Использование принципа гибридизации расширяет возможности регулирования характеристик механических свойств композиционных материалов с целью достижения технологически приемлемого равновесия между преимуществами и недостатками, присущими любому композиту [1–3]. Такие композиции с успехом применяются в авиацион-

ных обшивочных конструкциях, лопастях вертолетных винтов и ветрогенераторов, объектах строительной техники, корпусах автомобилей и яхт и др. [4, 5].

Чаще всего полимерные композитные материалы с несколькими типами армирующего наполнителя используют в виде слоистых тонкостенных панелей, которые представляют собой объединение слоев с более жестким высокомодульным (high modulus) наполнителем со слоями низкомодульного (low modulus), но более прочного компонента. Прочность гибридной композиции при растяжении определяется соотношениями, следующими из правила смеси, и зависит от степени гибридизации, которая может быть оценена объемной долей высокомодульного компонента [3, 6].

и |_ 0СМ1ЛМЕ

АППАРАТЫ VI технологи ш^ин

Том 9

Из-за различия в деформативных и прочностных свойствах компонентов слоистого гибрида при монотонном нагружении разнородные слои разрушаются при совместной деформации неодновременно из-за различия в их предельных деформациях. Эту особенность механизма разрушения слоистых гибридов следует учитывать при оценке предельного состояния элементов конструкций, долговечности и трещиностойкости гибридных панелей [6].

В еще большей степени эта особенность сказывается на устойчивости гибридных панелей, так ¹⁶⁸ как при изгибе деформация слоев композитной среды неравномерна по толщине и зависит от расположения слоя в общем пакете. Это объектив-

но ускоряет процесс более раннего разрушения высокомодульных слоев с меньшей предельной деформацией. Поэтому деформация удаленных от срединной поверхности слоев высокомодульного компонента может достигнуть предельной

в ряд, методы Рэлея-Ритца, расширенный метод Канторовича, безэлементный метод Галеркина, метод подвижных наименьших квадратов Ритца и др., обладают высокой точностью, но являются трудоемкими при расчетах композитных конструкций со сложной геометрией и нетрадиционными граничными условиями. В настоящее время появились более производительные бессеточные методы [10], методы дифференциальных квадратур [16], методы дискретной сингулярной свертки [17], которые становятся все более популярными при численном решении начальных и краевых задач в инженерных приложениях.

2. Постановка задачи

величины задолго до наступления критического состояния всей слоистой конструкции. Но опыт показывает, что для некоторых вариантов структуры гибридной композиции преждевременное разрушение отдельных высокомодульных слоев не приводит к полной потере устойчивости всей панели вследствие перераспределения нагрузки между неразрушенными слоями. Несущая способность панели в этом случае во многом определяется структурными параметрами слоистой среды – степенью гибридизации (количеством слоев разной природы) и последовательностью укладки разнородных слоев.

В данной работе проведено исследование устойчивого состояния стеклоуглепластиковых панелей различной структуры при сжатии и сдвиге и дана оценка влияния разрушения перегруженных слоев гибридной пологой панели на критические усилия потери устойчивости в зависимости от последовательности укладки слоев, радиуса кривизны поверхности и граничных условий.

1. Обзор опубликованных материалов

Поведение многослойных ортотропных и анизотропных тонкостенных элементов конструкций под нагрузкой изучали многие исследователи [7–12], которыми были предложены различные кинематические модели для прогнозирования устойчивости и динамического поведения композитных конструкций на основе различных подходов теории анизотропных пластин и оболочек. Как правило, для решения задач на собственные значения композитных элементов ортогональной формы применяют приближенные аналитические или численные методы. Известные вычислительные процедуры [13–15], такие как разложение

При заданных геометрических параметрах панели (размеры сторон, радиусы кривизны), материалов элементарных слоев композита (модули упругости вдоль и поперек волокон, модуль сдвига, коэффициент Пуассона, толщина слоя, напряжения вдоль и поперек слоя, касательное напряжение), числа слоев в пакете и структуры армирования каждого слоя находятся мембранные и изгибные жесткости панели.

Решается задача на собственные значения и определяются собственные значения и принадлежащие им собственные векторы и собственные формы. Находятся минимальные собственные значения – коэффициенты устойчивости и критические усилия сжатия и сдвига, а также принадлежащие им собственные векторы и собственные формы. Панель после потери устойчивости нагружается контурным усилием в долях критического усилия, решается задача закритического деформирования при аппроксимации прогиба в виде произведения неизвестной амплитуды и минимальной собственной формы. Из решения нелинейной задачи определяются амплитуда прогиба и напряженно-деформированное состояние каждого композитного слоя.

Выполняется оценка несущей способности панели по моменту разрушения наиболее нагруженного слоя/слоев различной структуры с использованием критерия прочности Цая-Ву [18]. При пошаговом нагружении панели контурными усилиями сжатия T _x или сдвига T _xy по значениям компонент тензора напряжений каждого слоя £ 1 ⁽ i ) , £ 2 i ) , т^ ) вычисляют коэффициенты нагружен-ности слоев

F^(Т ) = p xy

(1) Y

£ 1

( i )

V °1 в )

+

/ ( i ) V £ 2

( i )

V ° 2 в 7

—

£ 1 ⁽ i ) £ 2 i )

V ° 1 в    ° 2 в У

+

(  ( i ) А

V ^Т 12 в 7

и устанавливается предельное усилие { T Xi ; T y ) p } , при котором в наиболее нагруженном i -ом слое коэффициент нагруженности F p ) ^ 1. Этот уровень нагружения соответствует исчерпанию не-

сущей способности данного слоя и окончанию первого этапа нагружения. Далее в рамках принятой модели этот поврежденный слой заменяют фиктивным слоем, обладающим механическими свойствами связующего, и проводят проверку прочности панели с учетом замены поврежденного слоя. В случае выполнения условия прочности для всего пакета после такой замены продолжают пошаговое увеличение нагрузки и послойный анализ нагруженности. Следующий этап заканчивается после достижения предельного состояния в следующем перегруженном слое (слоях) заменой его фиктивным слоем связующего и пересчетом напряженно-деформированного состояния новой структуры с возможным переходом к очередному этапу нагружения. Анализ послойного разрушения гибридных панелей, выполненный в работе, был ограничен пятью этапами нагружения.

Результатом алгоритма исследований служит определение на каждом этапе критических усилий сжатия и сдвига, а также предельные разрушающие усилия для каждого этапа (в статье не приводятся), позволяющие оценить влияние на них послойного разрушения слоев гибридного материала.

• 3.    Собственные значения и собственные формы панели из гибридных материалов

Рассмотрим пологую композитную панель из гибридного материала с отношением сторон a / b = 2 ( a = 2 м; b = 1 м), радиусами кривизны R x ^ от, R y = [от, 100, 50, 25, 10, 5} м, нагруженную контурными усилиями сжатия T _x и сдвига T _xy (рисунок 1). Панель п рин ято сч ита ть пол ого й при соотношении ее размеров и радиусов кривизны не менее 1/5, линейные размеры образующих поверхности панели примерно равны их проекции на плоскость. Панель имеет симметричную структуру армирования относительно срединной поверхности и состоит из блоков слоев стеклоткани

• (1)                                              (2)

толщиной 8^ ^J и углеродной ленты толщиной 8^ . Каждый слой определяется углом армирования φ .

Рассмотрены два тестовых варианта структуры стекло- и углепластиковой панели, сформирован- ные из 8 шестислойных блоков слоев стеклоткани (glass) (блоки G1, G2) и углеродной ленты (carbon) (блоки C 1, C 2) с двумя версиями укладки слоев в блоках - [0О/0О/+45О/-45О/0О/0О] и [00/900/+450/450/+450/-450]. Вариант А структуры панели соответствует последовательности укладки блоков [C 1/G2/C 1/G2]2s, вариант Б – [G1/C 2/G1/C 2]2s.

Характеристики механических свойств углепластика до разрушения слоя:

E 1 = 149 ГПа; E ₂ = 7,45 ГПа;

G 12 = 2,8 ГПа; μ 21 = 0,3,

σ 1 = (+2970 / –1000) МПа;

,₂ = (+434 / -210) МПа; т ₁₂ = 109 МПа;

после разрушения слоя: E 1 = 7,45 ГПа; E ₂ = 7,45 ГПа; G 12 = 2,8 ГПа;

σ 1 = (+434 / –210) МПа;

^ 2 = (+434 / -210) МПа; т 12 = 109 МПа;

Характеристики механических свойств стеклопластика до разрушения слоя:

E 1 = ⁵⁰ ГПа; E 2 = ¹⁶ ГПа; G 12 = 5,2 ГПа; _Л 21 = ^0,2^3,

σ 1 = (+1080 / –540) МПа;

5₂ = (+930 / -240) МПа; т ₁₂ = 96 МПа;

после разрушения слоя: E ₁ = 16 ГПа; E ₂ = 16 ГПа; G 12 = 5,2 ГПа;

σ 1 = (+930 / –240) МПа;

, 2 = (+930 / -240) МПа; ^т ,2 = 96 МПа;

Толщины слоев углепластика и стеклопластика соответственно равны 8(1) = 0,125 мм и 8И = 0,25™'

При исследовании прочности панели из гибридного материала с разрушающимися слоями будем опираться на решение геометрически нелинейной задачи закритического деформирования [9], из которой найдем критические усилия сжатия и сдвига и предельные усилия, приводящие к разрушению отдельных слоев композита. Решение задачи на собственные значения панели выполним с помощью метода Рэлея-Ритца, для чего функцию перемещений представим в виде двойного ряда, образованного «балочными» функциями [11]

а)                                                                           б)

Рисунок 1. Схемы нагружения пологой панели: а) – сжатие; б) – сдвиг

w = ЕЕ AmnWlm (x) wn (У ).

m = 1 n = 1

det [Q]-L4J[(x]

—

Для определения минимальных собственных значений и принадлежащих им собственных векторов и форм полную потенциальную энергию E панели площадью S представим в форме Брайана [19]:

ab

E=2 {JiM :.Г +2 D2 (-ЛКИ

^{+ D} 22 ( w y ) ^{2 + 4 D} 33 ( w , xy ) ^{2 + B} 22 ^кУ ⁽ w ^{) 2} -      ⁽²⁾

- Nx ( w x ) ² - 2 Ny ( w x )( w , У ) } dxdy.

Подставив в фун к цио нал энер гии E прогиб (1), вычислим интеграл (2) методом Симпсона [19], согласно которому область интегрирования разбивается на i х j ячеек сетки при i е { 0,... , i _max } , j е { 0 ,..., j _max } . Минимизируя получающееся после интегрирования выражение по каждому элементу неизвестного вектора амплитуд [ A J , получим однородную систему линейных алгебраических уравнений:

Н^ *M (w П^

LAJ 0,                       (3)

где            -             ,   „

И=иЦfL w.....,,> w „лDr

L w xx , w , yy ^,2 w , xy J dxdy ,

ab                   ab

[ t x ] = J J ( w x ) 2 dxdy , L t xy J = J J 2 ( w x )( w y ) dxdy ; 00                    00

L A x J , L^ xy J - векторы собственных значений.

Условие равенства нулю определителя одно родной системы уравнений (3)

Том 9

B 22 k y ²

D 11 D 22

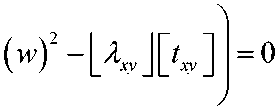
позволяет определить векторы собственных значений |_ A J , L A y J , а также несколько первых собственных векторов L q 1 J , L q ₂ J , L q₃ J ,..., соответствующих собственным значениям А 1 <  Л ₂<  Я 3... Затем вычисляем необходимые для аппроксимации за-кри т ического прогиба собственные формы в виде

W i

Е q p w i ( ^x ) ^w 2 ( y )

I p

> , где p - число членов ряда

На рисунке 2 приведены собственные формы, соответствующие минимальным собственным значениям-коэффициентам устойчивости изотропной панели при сжатии и сдвиге ( a = 2 м ; b = 1 м ; R_y = 50 м ; h = 2 мм ; / = 0⁰ ) .

Полагая, что форма закритического прогиба, при которой происходит разрушение перегруженного слоя, будет подобна первой собственной форме (форма соответствует минимальному собственному значению), переходим к решению задачи о закритическом деформировании пологой панели. Форма закритического прогиба

w zk = A Е q,w ( x ) w 2 ( y ) ; p = b³⁰. (4) ^p

Меняя уровень нагружения панели усилиями сжати я или сдвига, определяем момент, при котором в наиболее нагруженном слое композита выполнится условие F^ = 1.0 При поиске наиболее нагруженного слоя нео^.бходимо исследовать напряженное состояние в каждом узле сетки и каждом слое, которые подлежат анализу. Точность результатов расчетов предельных усилий сжатия и сдвига вытекает из погрешности аппроксимации закритического прогиба (4), шага разбиения сетки и погрешности при выполнении условия F^ = 1.0. Заменив в разрушенном слое исходные характеристики механических свойств на характеристики после разрушения слоя, повторяем расчет с новыми жесткостными и проч-

А                Б

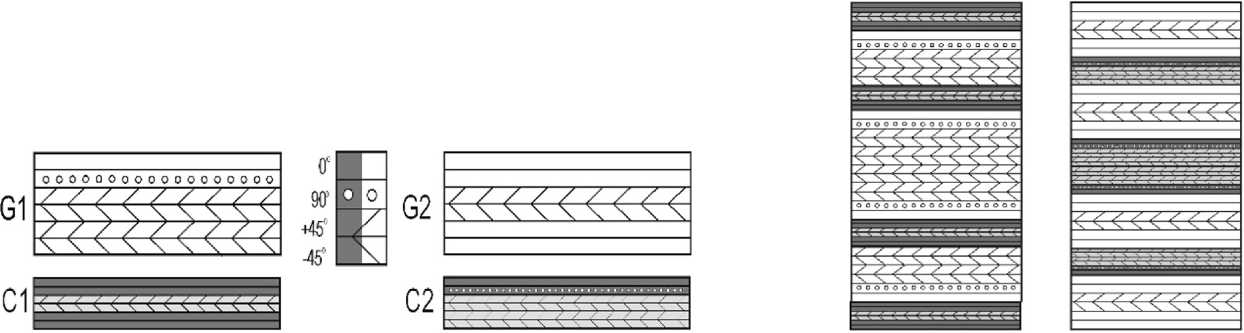
а)                                                              б)

Рисунок 2. Варианты укладки слоев гибридного композита: а) – блоки, б) – панели

ностными свойствами пакета слоев панели при сжатии и сдвиге.

Каждое исследование варианта армирования, радиуса кривизны, вида контурного усилия и граничных условий включало 5 этапов, на каждом из которых нагружение пологой панели доводилось до разрушения наиболее нагруженного слоя композитного материала. Жесткостные и прочностные характеристики панели определялись с учетом разрушенных на предыдущих этапах слоев в предположении, что для пакета слоев остается справедливой гипотеза Киргофа-Лява.

• 4.    Панель нагружена сжимающими усилиями в продольном направлении

• 5.    Панель нагруженакасательными усилиями сдвига

Результаты исследования послойного разрушения прямоугольной панели с разной кривизной в поперечном направлении на критические усилия сжатия приведены в таблицах 1 и 2. В таблице 1 показано изменение критических усилий сжатия панели со свободно опертыми кромками для двух вариантов армирования; в таблице 2 – изменение критических усилий сжатия панели с защемленными кромками. Сравнение результатов расчетов показывает, что вариант армирования Б более предпочтителен по устойчивости панели как со свободно опертыми кромками, так и с защемленными кромками. На рисунках 3 и 4 приведены графики изменения критических усилий сжатия в зависимости от радиусов кривизны и этапа нагружения для гибридной панели с различными 171 граничными условиями.

В таблицах 3 и 4 приведены результаты изменения критических усилий сдвига пологой ги-

Таблица 1

	N xkr( кH / м )
	R y = ∞	R y = 100 м	R y = 50 м	R y = 25 м	R y = 10 м	R y = 5 м
этап	вариант А
1	85,11	87,34	94,05	120,91	204,23	346,04
2	85,10	87,34	94,05	120,93	204,27	346,14
3	85,09	87,34	94,05	120,95	204,26	346,17
4	84,98	87,34	94,05	120,86	203,86	345,59
5	84,81	87,34	94,05	120,73	203,24	344,67
этап	вариант Б
1	115,63	118,45	126,91	159,02	255,02	427,08
2	114,78	118,45	126,91	157,12	251,64	421,85
3	109,74	118,45	126,91	145,70	231,35	390,17
4	109,74	113,41	126,07	142,22	226,18	363,19
5	109,74	112,55	121,02	137,96	220,61	337,40

Таблица 2

	N xkr( кH / м )
	R y = ∞	R y = 100 м	R y = 50 м	R y = 25 м	R y = 10 м	R y = 5 м
этап	вариант А
1	169,81	171,58	176,8	190,19	261,81	404,53
2	169,80	171,58	176,8	190,19	261,81	404,63
3	169,78	171,58	176,8	190,19	261,87	404,63
4	169,54	171,58	176,8	190,19	261,87	403,82
5	169,18	171,58	176,8	190,19	261,87	402,57
этап	вариант Б
1	227,48	228,61	231,98	245,3	332,09	498,69
2	227,48	225,51	228,87	245,3	332,09	491,69
3	224,38	206,96	210,28	242,2	327,31	448,98
4	205,85	206,96	210,28	242,2	327,31	415,55
5	205,85	206,95	210,28	223,4	298,39	383,63

ОСМИЧЕСКИЕ АППАРАТЫ И

ТЕХНОЛОГИИ нш

Том 9

а)                                                            б)

Рисунок 3. Собственные формы, соответствующие минимальным собственным значениям: (а) – при сжатии и (б) – сдвиге

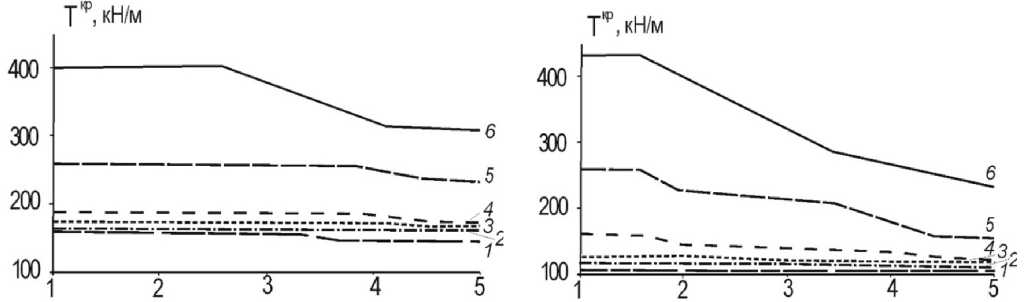
а)                                                            б)

Рисунок 4. Влияние кривизны панели и этапов нагружения на критические усилия сжатия N_xkr ( кH / м ) панели со свободно опертыми кромками:

• (а) – вариант А; (б) – вариант Б; 1 – R _y = ∞; 2 – R _y = 100; 3 – R _y = 50; 4 – R _y = 25; 5 – R _y = 10; 6 – R _y = 5

  Критические усилия сдвига панели со свободно опертыми кромками

  
  

  Критические усилия сдвига панели с защемленными кромками

  
  

Таблица 3

	N xykr ( кH / м )
	R y = ∞	R y = 100 м	R y = 50 м	R y = 25 м	R y = 10 м	R y = 5 м
этап	вариант А
1	121,84	125,12	133,47	156,02	229,03	365,60
2	121,72	124,81	132,89	154,88	218,08	359,71
3	115,47	118,44	126,18	147,24	215,13	342,36
4	115,47	118,44	126,18	147,25	211,01	342,36
5	115,46	118,44	126,18	147,25	206,96	342,56
этап	вариант Б
1	172,20	176,04	186,15	214,20	308,51	487,53
2	169,08	172,80	182,61	209,90	282,30	476,02
3	165,03	168,64	178,14	204,61	258,50	462,80
4	149,34	152,82	161,91	186,79	250,46	427,88
5	131,65	135,00	143,63	166,70	243,67	388,55

Таблица 4

	N xykr ( кH / м )
	R y = ∞	R y = 100 м	R y = 50 м	R y = 25 м	R y = 10 м	R y = 5 м
этап	вариант А
1	189,66	190,82	194,18	205,95	260,91	379,71
2	189,40	190,52	193,74	205,11	258,48	362,12
3	180,56	170,79	173,77	195,54	246,40	356,72
4	180,55	170,79	173,77	195,55	246,44	349,75
5	180,54	170,77	173,77	195,54	246,46	342,91
этап	вариант Б
1	264,93	266,29	270,24	284,39	353,74	508,08
2	260,49	256,52	260,26	279,31	346,61	467,79

Окончание таблицы 4

	N xykr( кH / м )
	R y = ∞	R y = 100 м	R y = 50 м	R y = 25 м	R y = 10 м	R y = 5 м
3	254,74	250,72	231,18	272,91	338,03	430,98
4	231,94	227,88	205,69	249,60	310,89	428,00
5	226,66	202,54	205,69	222,56	280,34	416,74