Исследование вариантов перехода от неограниченного параллелизма к ограниченному на примере умножения матриц

Введение. Существует множество различных подходов для разработки параллельных программ. При параллельном программировании часто применяются специальные приемы программирования и в большинстве случаев считается более эффективным написание кода программы под определенную вычисленную систему. А так как развитие вычислительной техники сегодня идет бурными темпами, то зачастую программистам приходится переписывать код под новую недавно разработанную систему. Основная проблема перехода от традиционного программирования к параллельному состоит в том, что невозможно разработать универсальный исполнитель, с помощью которого можно бы было достичь одинакового эффективного способа написания параллельных программ [1–3]. Помимо стиля написания программ в той или иной системе также необходимо учитывать количество используемых ресурсов и их вычислительную мощность. Следовательно, для осуществления эффективных параллельных вычислений приходится постоянно перестраивать структуру программы.

Вопрос о создании инструментальных средств, обеспечивающих переносимость параллельных программ, изучается уже достаточно давно. И все попытки разработать такие системы были связаны с написанием программ для обобщенной архитектуры [4].

Предлагается поставить акцент не на особенностях той или иной ВС, а использовать некую абстрактную систему, позволяющую стремиться к повышению эффективности кода за счет разработки программ с неограниченным параллелизмом. Повышая уровень абстракции, есть возможность построения различных комбинаций, сжимая параллелизм, и следовательно, перехода от неограниченного параллелизма к ограниченному.

В качестве математического аппарата в исследовании рассматривались различные подходы к описанию алгоритмов для повышения их реализации, в том числе подход, основанный на неограниченном параллелизме. Предлагается подход, в основе которого лежат различные ограничения на параллелизме. В ходе работы подробно изучались последовательные и параллельные методы умножения матриц, в том числе ленточные и блочные алгоритмы. После проведения декомпозиции в рамках решения задачи умножения матриц были предложены различные варианты последующего суммирования полученных результатов решения подзадач для повышения эффективности использования ресурсов последовательным способом и по каскадной схеме.

Данные исследования можно применять в различных областях науки, в том числе и для разработки программного обеспечения в ракетостроении, что позволит в дальнейшем усовершенствовать систему управления ракетой.

Алгоритм решения проблемы.

Постановка задачи. На самом деле постановка задачи выглядит следующим образом. Перемножаются две матрицы: A[M][L] * B[L][N] => C[M][N], где количество перемножений строк на столбцы S = M * N.

В каждой комбинации перемножения строки на столбец участвует L пар элементов.

Поэтому общее число одновременно возможных перемножений P = M * N * L, то есть, задается соответствующим параллелепипедом [5; 6].

Далее перемножаемые элементы для каждой комбинации строки и столбцах начинают складываться. При этом возможно использование обычного последовательного метода сложения или по каскадной схеме.

Матричное умножение. Операции с матрицами являются довольно трудоемкими для их реализации, поэтому они представляют собой классическую область применения параллельных вычислений.

Последовательный алгоритм умножения матриц. Если имеются две квадратные матрицы А и В, то С=А*В – результат их умножения

C ij =∑ⁿ k-1 =a ik * b kj , где i=1,…,n. j=1,…,m .

Этот алгоритм умножения двух матриц A и B является итеративным и ориентирован на последовательное вычисление строк матрицы С (рис. 1). При выполнении одной итерации внешнего цикла вычисляется одна строка результирующей матрицы [7].

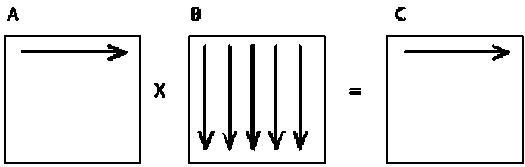
Рис. 1. Первая итерация умножения матриц при последовательном подходе

Fig. 1. First iteration of matrix multiplication in a sequential approach

В последовательном алгоритме матричного перемножения идет поэлементное умножение всех элементов матрицы. Информационный граф в таком случае будет довольно объемным и поэтому его анализ затруднен. Кроме того, этот способ перемножения становится неэффективным, если размер матрицы превышает объем кэш-памяти процессора. Необходим поиск более эффективных алгоритмов решения этой задачи [8; 9].

Из формулы (1) ясно, что вычисление каждого С ij осуществляется независимо и одновременно и может быть выполнено параллельно. Этот алгоритм с массовым параллелизмом, так как он содержит огромное количество операций, которые могут выполняться одновременно и независимо друг от друга [9].

Выбор способа разделения матриц приводит к определению конкретного метода параллельных вычислений. Существование разных схем распределения данных порождает целый ряд параллельных алгоритмов матричных вычислений.

Если абстрагироваться от использования конкретных ресурсов для решения задачи, то можно добиться повышения эффективности программ, постепенно сжимая первоначально неограниченный параллелизм.

Процесс умножения в данном случае будет начинаться с декомпозиции задачи на подзадачи. То есть для решения задачи (1), рассматриваются основные комбинации перемножаемых элементов матриц по i, j, k .

Возможны варианты, когда параллельно вычисляются результирующие строки, столбцы или группы столбцов матриц. К примеру, если выполнять тело цикла по i для каждого значения счетчика параллельно, то параллельно будут насчитываться строки произведения матриц. Если же поменять местами циклы по i и по j (что вполне возможно по причине независимости операций вложенных циклов по i и по j ) и выполнять параллельно тело цикла для каждого значения счетчика, то получится вариант программы, параллельно насчитывающий столбцы. Кроме того, можно также параллельно насчитывать каждый элемент результирующей матрицы [9].

Сокращение шагов при перемножении матриц и переход к параллельным алгоритмам. Как было отмечено выше, из определения операции умножения матриц А и В следует, что нахождение элементов результирующей матрицы С можно производить независимо друг от друга. Произведение матриц может рассматриваться как n ² независимых скалярных произведений либо как n независимых произведений матрицы на вектор. В обоих случаях используются разные алгоритмы [10].

В первом подходе для организации параллельных вычислений в качестве основной подзадачи используется процедура определения одного элемента результирующей матрицы С, при этом для осуществления всех необходимых вычислений каждая задача должна содержать хотя бы одну строку матрицы А и столбец матрицы В. Общее количество подзадач здесь n ². Во втором подходе для выполнения всех необходимых вычислений базовой подзадаче должны быть доступны одна из строк матрицы A и все столбцы матрицы B. Количество подзадач – n [11].

Для повышения эффективности алгоритма матричного умножения логично предположить, что если производить операции умножения матриц не поэлементно, а построчно, то это позволит добиться большей эффективности алгоритма с точки зрения параллелизма. В таком случае общая задача матричного умножения будет сводиться к разбиению ее на подзадачи. Далее эти подзадачи будут объединены для получения общего необходимого решения первоначальной задачи.

Из вышесказанного следует, что этот алгоритм можно рассмотреть как процесс решения независимых подзадач умножения матрицы А на столбцы матрицы В. И при этом информационный граф упрощается, в отличие от случая с последовательным алгоритмом умножения. Те есть все сводится к построению графа матричного умножения. Введение макроопераций осуществляется поэтапно с возвращаемым уровнем детализации используемых операций или декомпозиции [12].

Ленточный алгоритм. Рассмотрим ленточные алгоритмы, в которых матрицы A и B разбиваются на непрерывные последовательности строк или столбцов (рис. 2). Для осуществления этой процедуры в каждой подзадаче содержится строка А матрицы и имеется доступ к столбцам В. Одному процессору выделяется то или иное количество строк и столбцов. Простое решение этой проблемы – дублирование матрицы B во всех подзадачах. Здесь возможен следующий способ организации параллельных вычислений для матриц 3*3 [13]:

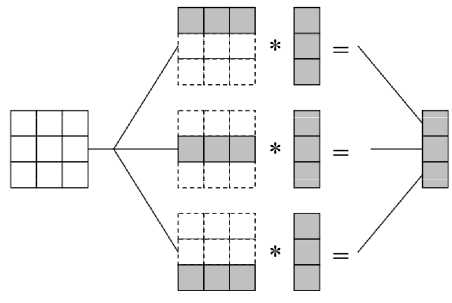
Рис. 2. Пример организации вычислений в алгоритме матричного умножения, основанного на разделении матриц на строки

Fig. 2 The example of the organization of calculations in a matrix multiplication algorithm based on dividing matrices into rows

Такие мелкозернистые задачи можно укрупнять, если размер матрицы оказывается больше числа вычислительных элементов или процессоров. В этом случае исходная матрица A и матрица результирующая С разбиваются на горизонтальные полосы. Размер таких полос при этом следует выбрать равным k = n/p (если n кратно p ), что позволяет по-прежнему обеспечить равномерность распределения вычислительной нагрузки по вычислительным элементам [13].

Выделенные базовые подзадачи характеризуются равным объемом передаваемых данных и одинаковой вычислительной трудоемкостью. В случае, когда размер матриц получается больше, чем число вычислительных элементов (процессоров и/или ядер) p , базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько соседних строк матрицы. В таком случае результирующая матрица С и исходная матрица A разбиваются на ряд горизонтальных полос [13].

Данный ленточный алгоритм обладает хорошей локализацией, и вдобавок, в нем нет взаимодействия между потоками данных. Но следует заметить, что если укрупнить подзадачи, то можно перейти к другим более эффективным с точки зрения параллелизма алгоритмам умножения матриц – к блочным алгоритмам.

Переход к блочным алгоритмам. В таких алгоритмах исходные матрицы А, В и результирующая матрица С представляются в виде наборов блоков.

В этом случае не только результирующая матрица, но и матрицы-аргументы умножения матриц разделяются между потоками параллельной программы на некие прямоугольные блоки. Этот подход позволяет добиться хорошей локализации данных и повысить эффективность использования кэш-памяти.

Также известны параллельные алгоритмы умножения матриц, основанные на блочном разделении данных, ориентированные на многопроцессорные вычислительные системы с распределенной памятью. При разработке алгоритмов, ориентированных на использование параллельных вычислительных систем с распределенной памятью необходимо учитывать, что размещение всех требуемых данных в каждой подзадаче (в данном случае – размещение в подзадачах необходимых наборов столбцов матрицы В и строк матрицы А) неизбежно приведет к дублированию и к значительному росту объема используемой памяти. В результате на систему накладываются некоторые ограничения, то есть вычисления должны быть организованы таким образом, чтобы в каждый текущий момент времени подзадачи содержали лишь часть необходимых для проведения расчетов данных, а доступ к остальной части данных обеспечивался бы при помощи передачи сообщений. К числу алгоритмов, реализующих описанный подход, относятся алгоритм Фокса и алгоритм Кэннона [14] (рис. 3).

Отличие этих алгоритмов состоит в последовательности передачи матричных блоков между процессорами любой вычислительной системы.

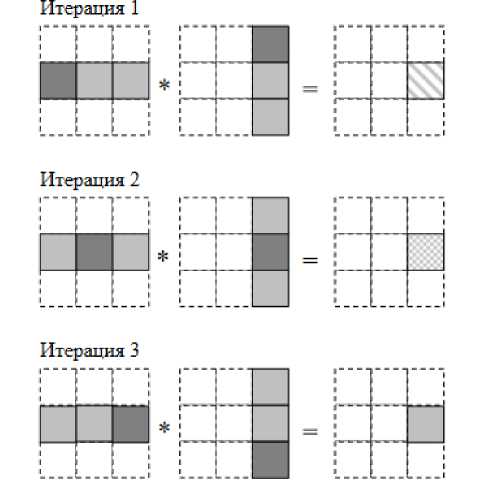
Рис. 3. Схема организации блочного умножения полос матрицы

Fig. 3. Block matrix organization scheme

Следует отметить, что после этапа декомпозиции с выделением подзадач и поиском эффективного параллельного алгоритма, необходимо произвести суммирование полученных решений от подзадач для получения общего результата решения задачи матричного умножения.

С точки зрения параллелизма, можно применять в данном случае не только последовательное суммирование, но и более эффективные параллельные методы, например, сложение по каскадной схеме (рис. 4).

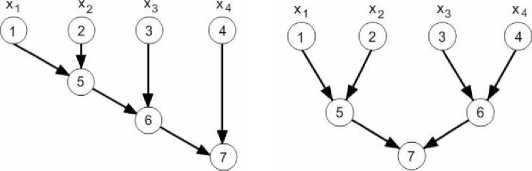
Рис. 4. Графы алгоритмов последовательного (слева) и каскадного суммирования (справа) [15]

Fig. 4. Graphs of sequential (left) and cascade summation algorithms (right) [15]

Заключение. После проведенного анализа вышеописанных алгоритмов, планируется полученные результаты использовать для поиска возможностей эквивалентных преобразований различных алгоритмов и разработки автоматизированной системы (некой базы знаний), позволяющей ее пользователю выбирать тот или иной алгоритм для решения своей задачи для того, чтобы добиться наиболее быстрого и эффективного решения с точки зрения использования ресурсов.

Использование алгоритмов, описывающих максимальный параллелизм решаемой задачи, предлагает разработчику дополнительные методы для анализа и вывода разнообразных алгоритмов с ограниченным параллелизмом, которые могут рассматриваться как варианты использования.

Рассмотрение всех алгоритмов, изученных в данной работе, а также, их реализация на функционально-потоковом параллельном языке, позволяющем выполнять операции с максимальным параллелизмом, открывает перспективы на дальнейшую разработку и усовершенствование методов и подходов повышения эффективности программ.

Acknowledgments. This work was supported by the financial support of the Russian Fund of Federal Property in the framework of the scientific project No. 17-07-00288 A.