Исследование виброизоляции промышленной швейной машины

В известной литературе [1 - 4] отсутствуют сведения по исследованию виброизоляции промышленных швейных машин.

Отсутствие исследований не позволяет на стадии проектирования оптимизировать уровни колебаний платформы и промстола швейной машины, с которыми контактируют руки оператора. Например, в швейных машинах фирмы «Typical» GC6720HD и Оршанского завода «Легмаш» 31-го ряда уровни виброскорости платформы и промстола различаются на 10 - 15 дБА при равных требованиях, предъявляемых к этим поверхностям. В связи с этим возникает задача выравнивания уровней виброскорости на платформе и крышке промстола, что должно привести к их уменьшению.

В настоящей работе поставлена задача разработки приближённой математической модели колебательной системы швейной машины с включением в неё виброизолирующих прокладок, что позволяет на стадии проектирования оптимизировать параметры виброскорости.

В настоящей работе предложена приближённая математическая модель колебательной системы швейной машины с включением в неё виброизолирующих прокладок.

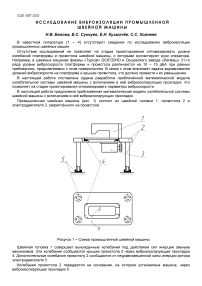
Промышленная швейная машина (рис. 1) состоит из швейной головки 1, промстола 2 и электродвигателя 3, закреплённого на промстоле.

Рисунок 1 - Схема промышленной швейной машины

Швейная головка 1 совершает вынужденные колебания под действием сил инерции звеньев механизмов. Эти колебания сообщаются крышке промстола 2 через виброизолирующие прокладки 4. Дополнительные колебания промстолу 2 сообщаются от неуравновешенной силы инерции ротора электродвигателя 3.

Колебания промстола 2 передаются на основание, на котором установлена машина, через виброизолирующие прокладки 5.

При работающей швейной машине колебания плоской платформы швейной головки и крышки 2 промстола могут передаваться на руки швей. Эти колебания не должны превышать уровней, предписанных санитарно-гигиеническими нормами [5].

Представим математическую модель колебаний швейной машины в виде системы с 2-мя степенями свободы (рис. 2 а).

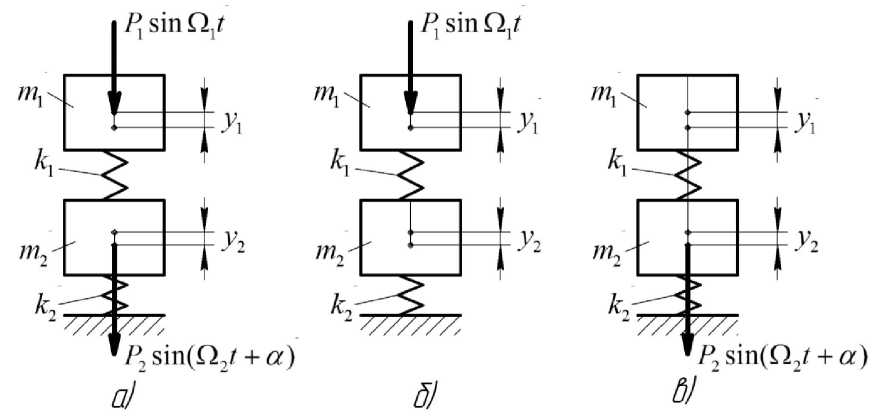
Рисунок 2 - Модели колебательных систем: а) модель 1; б) модель 2; в) модель 3

На рис. 2 а изображены:

т 1 — масса швейной головки, кг;

к 1 — коэффициент упругости виброизолирующих прокладок швейной головки (поз. 4 на рис. 1), Н/м;

m 2 — масса промстола и электродвигателя (поз. 2, 3 на рис. 1), кг;

k 2 — коэффициент упругости виброизолирующих прокладок промстола (поз. 5 на рис. 1), Н/м;

P 1 — амплитуда суммарной силы инерции механизмов швейной машины, Н;

Й 1 — угловая скорость главного вала швейной головки, рад/с;

P 2 — амплитуда неуравновешенной силы инерции ротора электродвигателя, Н;

^ 2 — угловая скорость ротора электродвигателям, рад/с.

Предполагается, что суммарная сила инерции механизмов швейной головки PГ изменяется по закону P_Y = Р_г5i ni₁t , а неуравновешенная сила инерции ротора электродвигателя — по закону Р _Э = P₂ s in(/2₂t + а) .

Решение уравнений колебаний представленной модели 1 является достаточно сложным, поэтому рассмотрим колебания этой модели в виде суммы колебаний более простых систем: модели № 2 и модели № 3 (рис. 2 б, 2 в).

Уравнение колебаний модели 2 имеет вид:

т1У 1 + к!(у1 - у2) = P iSiniTt,(1)

т2у2 + к2у2 - к 1(у 1 - у2) = 0.(2)

Ищем решения системы (1), (2) в виде:

у1 = A isiniit,(3)

у₂ = A ₂s i ni ₁1 .

Подставив (3), (4) и их вторые производные в (1), (2), рассмотрим условия, при которых (3), (4) превращаются в тождества. В результате получим систему линейных уравнений относительно A 1 , A 2 , решая которую получим выражения для определения амплитуд колебаний:

Д _ _____ Р 1 ⁽ к 1 + ^к1 - ^m1^Д 1 ) _____

¹     (к 1 -zn i ti^^ i +fc i -п^Д¹)- к¹ ’

А о = т/1к 1..

• ¹    (к 1 -т 1 Д¹)(к 1 +к 1 -п^Д¹)- к¹

Уравнение колебаний модели № 3 имеет вид:

m 1У 1 + к 1(у 1-У1 ) = 0,(7)

miyi + к1 yi - к1(у1 - У1) = Pisln(tii1 + а).(8)

Решение системы (7), (8) ищем в виде:

у 1 = Л 3s l п(Д i t + а),(9)

у1 = Л 4s1и(Д1t + а).(10)

Подставив (9), (10) и их вторые производные в (7), (8) и рассмотрев условия, при которых (7), (8) превращается в тождества, получаем систему линейных уравнений относительно A 3 , A 4 , решая которую определяем:

Л, =7 ,

• ³     (к 1 -т 1 Д¹ )(к 1 +к 1 -т 1 Д¹)-к 1 к 1

_________ ^(к 1^-m1 ^{Д 1 )р} 1 _________ ( к 1 —m 1 Д¹ )( к 1 +к 1 - m i ft ¹ ) —к 1 к i

Суммируя колебания моделей № 2 и № 3 получим:

у 1 = Л 1s l пД1 + Л 3 s 1п(Д 1t + а), у1 = Л 1s ln/211 + Л 4 s 1п(Д 1t + а).

Для проверки достоверности представленной модели колебаний швейной машины проведём экспериментальные исследования и расчёты по предлагаемым моделям 2 и 3 и сравним результаты.

Эксперимент проведён на серийном образце швейной машины 31-го ряда завода «Легмаш» (г. Орша). Замер показателей виброскорости проводился в точках Б швейной головки (см. рис. 1) и В промстола с помощью прибора ВШВ-003-М2 при частоте вращения главного вала швейной головки, равной 3000 об/мин. Съём информации о виброскорости в точках Б и В производился преобразователями пьезометрическими виброизмерительными ДН-ЗУ1 ТУ25-7706.019-88 и ДН-4-М1ТУ25-7705.020-86.

Результаты замеров приведены в верхней строке таблицы.

Таблица — Значения логарифмического уровня виброскорости в контрольных точках Б и В (положения точек указаны на рис. 1)

Метод определения	Lv , дБА
	точка Б платформы	точка В промстола
экспериментальный	87,5	73,5
расчётный	89	75

Для расчёта амплитуд колебаний по формулам (5), (6), (11), (12), (13), (14) необходимо иметь значения k 1 , k 2 , P 2 , m 1 , m 2 .

Коэффициенты упругости k 1 , k 2 виброизолирующих прокладок можно определить экспериментальным методом на приборе ЖНЗО-2, предназначенном для определения жёсткости деталей обуви.

Схема измерения показана на рис. 3 а. На рис. 3 б, 3 в показаны сечения виброизолирующих прокладок швейной головки (поз. 4 на рис. 1) и промстола (поз. 5 на рис. 1). На приборе замеряются деформации y виброизолирующих прокладок под действием груза P .

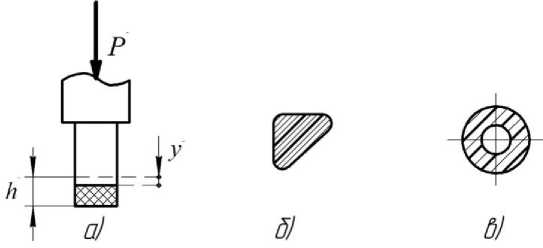
Рисунок 3 – Схема измерений коэффициентов упругости виброизолирующих прокладок

По результатам измерения деформаций y виброизолирующих прокладок швейной головки построен график зависимости y от P (рис. 4). Из графика видно, что коэффициент упругости      = dP _                .                                           .             . „ виброизолирующей прокладки не является величиной постоянной. Учитывая, что ay виброизолирующие прокладки 4 (см. рис. 1) предварительно сжимаются под действием силы веса G1 швейной головки, а амплитуда возмущающей нагрузки равна P1, принимаем коэффициент упругости k10 приближённо-постоянным и равным среднему значению на диапазоне изменения P от p .=  - ^1 до p =  +

=  - до      =  +   .

Тогда      =          , где ymax и ymin — значения y для Pmax и Pmin , полученные из графика на

Утах Ут1п рис. 4

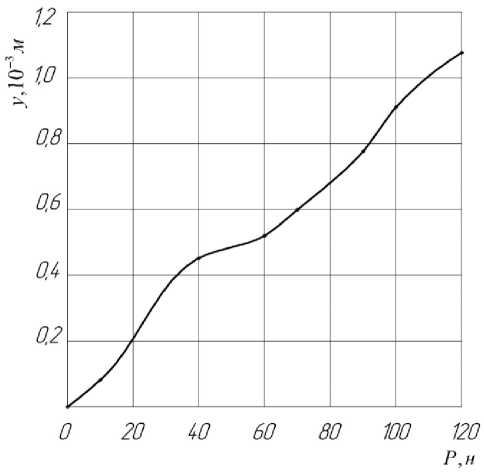
Рисунок 4 – График зависимости k 1 от P

Принимаем   G 1 = 294,3 Н, P 1 = 30 Н, получим P min = 60 Н, P max = 90 Н.   y min = 0,515∙10^-3 м;

y max = 0,785∙10^-3 м, k 10 = 111,1∙10³ Н/м.

Суммарный коэффициент упругости четырёх виброизолирующих прокладок составляет:

k 1 = 4 ∙ K 10 = 444,4∙10³ Н/м.

Аналогично определено значение k 2 для виброизолирующей прокладки промстола:

k 2 = 552∙10³ Н/м.

Выполним расчёт амплитуд вынужденных колебаний при следующих исходных данных:

m 1 = 30 кг; m 2 = 70 кг; Ω 1 = 314 рад/с; Ω 2 = 293 рад/с; k 1 = 444,4∙10³ Н/м, k 2 = 552∙10³ Н/м, P 1 = 35 Н.

Значение P 1 получено из результатов силового анализа механизмов швейных машин 31-го ряда завода «Легмаш».

В результате определены из формул (5), (6) A 1 = 13,7∙10^-6 м; A 2 = 0,92∙10^-6 м.

Значения A 3 , A 4 могут быть определены из формул (11), (12) при Ω 2 = 293 рад/с и известном P 2 . Значение P 2 зависит от балансировки ротора электродвигателя и не может быть определено теоретически. Поэтому определим P 2 экспериментальным методом для модели 3 (см. рис 2 в) колебательной системы. Эта модель может быть получена, если отсоединить от привода швейную головку и оставить включённым электродвигатель. Произведены замеры амплитуды A 3 колебаний в точке В (см. рис. 1) промстола с помощью прибора ВШВ-003-М2. A 3 = 0,5∙10^-6 м.

Этому значению A 3 согласно формуле (11) соответствует значение

Р 2 =

A 3 ⁽⁽ k^1-m1G 2 ⁾⁽ 14+1^ 2 0 2 ) ^-k1 . k²

=11,1 H .

k2

Подставляя это значение P 2 в формулу (13), получим

A 4 = 2,24∙10^-6 м.

Уравнения (13), (14) выражают суммы гармонических колебаний моделей 2 и 3 колебательной системы. Амплитудные значения этих колебаний не могут быть определены, т. к. неизвестен фазовый угол α .

В рассматриваемой колебательной системе доминирующими являются гармонические колебания, совершаемые под действием силы P 1 . Для приближённой оценки суммарных колебаний системы примем амплитуды колебаний в точках Б и В (см. рис. 1) равными соответственно:

^ сум . Б    ⁷ 1 + ~^i

• ⁷¹ сум . В   ⁷* 4 + 2 '

В результате получим:

A сум.Б = 14,16∙10^-6 м; A сум.В = 2,69∙10^-6 м.

Вычисление логарифмического уровня виброскорости L V гармонических колебаний при известной их амплитуде А произведём по формуле

L_v = 20tg- ,                            (15)

^o где V — среднегеометрическое значение скорости колебаний, м/с.

V = 0,707 A ∙ Ω 1 ,                            (16)

V 0 — базовое значение скорости колебаний, V 0 = 5∙10^-8 м/с.

Для вычисления значений A сум.Б и A сум.В получим L VƂ = 75 дБА, L VB = 89 дБА. Эти значения L V занесены в таблицу.

Из таблицы следует, что погрешность расчётного метода определения L V для контролируемых точек Б и В (см. рис. 1) составляет 1,7 % и 2 % и предложенная модель колебаний достаточно точно оценивает уровень колебаний системы.

В результате проведённых исследований впервые разработана приближённая математическая модель колебательной системы швейной машины с включением в неё виброизолирующих прокладок.

С использованием предложенной модели возможна оптимизация параметров виброизоляции с целью снижения вредного воздействия поверхностей стола и платформы на оператора.