Исследование вязкости полиэтилсилоксановых (ПЭС) жидкостей при малых градиентах скорости течения

Наличие низкочастотной (105 Гц) сдвиговой упругости жидкостей было обнаружено акусти- ческим резонансным методом с применением пьезокварцевого резонатора в виде прямоугольного бруска. Грань, колеблющаяся на резонансной частоте, контактирует на одном конце с прослойкой жидкости, накрытой твердой накладкой [1]. При тангенциальных смещениях пьезокварца прослойка жидкости испытывает деформации сдвига, и при этом меняются параметры резонансной кривой. Теория метода дает для комплексного модуля сдвига G* выражение:

4 р ² Mf o Дf*H

G* =------------- ,

S где М – масса пьезокварца;

f 0 – его резонансная частота;

A f* - комплексный сдвиг резонансной частоты;

H – толщина жидкой прослойки;

S – площадь контакта жидкости с пьезокварцем.

Для тангенса угла механических потерь будет иметь выражение:

tg 6 = AH .                                      (2)

A f'

Мнимый сдвиг резонансной частоты Af равен изменению полуширины резонансной кривой. В эксперименте применялся пьезокварц Х-18,5^о среза в форме прямоугольного бруска с резонансной частотой 74кГц, массой 6,24 г и размером 34,7х12х5,5 мм³. Площадь основания накладки составляла 0,2 см². Толщина жидкой прослойки определялась методом интерференции света в тонкой прослойке жидкости с точностью 0,01 мкм.

В работе [2] было показано, что при малых углах сдвиговой деформации наблюдается область линейной упругости, когда напряжение в прослойке жидкости оказывается пропорциональ- ным величине деформации. При дальнейшем возрастании угла деформации модуль сдвига уменьшается. Угол сдвиговой деформации при его малых значениях пропорционален отношению амплитуды колебания пьезокварца к толщине жидкой прослойки A/H. Амплитуда колебания пьезокварца определялась с помощью интерферометра Фабри-Перо [1, 3].

В наших экспериментах углы деформации не превышали 3-4⁰. Поэтому отношение A/H может служить мерой угловой деформации. Для удобства анализа экспериментальные результаты

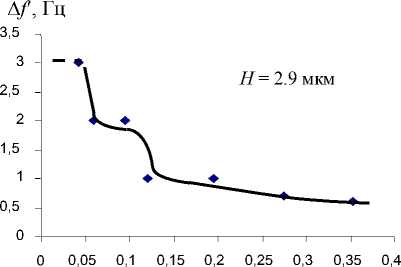
(A / H) ^1/2

Рис. 1. Зависимость A f от угла сдвиговой деформации для ПЭС-2

даются в зависимости от квадратного корня этого отношения.

На рисунке 1 показана зависимость действительного сдвига резонансной частоты пьезокварца от угла сдвиговой деформации для ПЭС-2 при температуре t=2° °C и толщине прослойки H=2,9 мкм. Из рисунка видно, что с увеличением угла сдвига A/H действительный сдвиг резонансной частоты Af уменьшается. Как видно из графика (пунктирные линии), для этой жидкости, в отличие от исследованных жидкостей в работах [1, 2], не удалось обнаружить область, соответствующую линейной сдвиговой упругости жидкости, где сдвиговое напряжение пропорционально сдвиговой деформации, поскольку не было возможности получить углы меньше критического угла сдвига . Для нашего случая критический угол сдвига фк ~ 8.4‘. Осо бенностью этой кривой является то, что первое резкое уменьшение Af' происходит при угле (A/H)1/2 ~ °,°5. Полагая, что исследуемая жидкость обладает развитой структурой со сравнительно большим периодом релаксации и с конечной прочностью, при малых углах сдвиговой деформации эта структура остается неизменной. При большем напряжении сдвига, соответствующего критическому углу сдвига, равновесная структура начинает разрушаться и действительный модуль сдвига уменьшается. По выражениям (1) и (2) можно рассчитать сдвиговую упругость G’ и tg6 при разных значениях амплитуды колебания.

В работе [4] было предположено, что при равновесной структуре эффективная вязкость может оказаться намного больше табличной вязкости , которая относится к жидкости с разрушенной пространственной структурой, соответствующей ламинарному течению жидкостей.

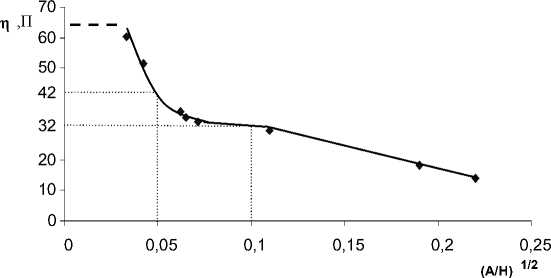
Рис. 2. Зависимость эффективной вязкости от угла сдвиговой деформации для ПЭС-2

На рисунке 2 представлена зависимость эффективной вязкости исследуемой жидкости ПЭС-2 от угла сдвиговой деформации, рассчитанная по реологической модели Максвелла:

η эф =

G( 1 + tg ²0 ) 2 n f o tg 9

Из рисунка 2 видно, что с увеличением величины угловой деформации A/H эффективная вязкость пэФ уменьшается, причем изменение вязкости жидкости происходит ступенчато, аналогично изменению модуля сдвига. Наглядно видна ньютоновская вязкость в виде площадки на гра- фике. При малых углах деформации эффективная вязкость ηэф соответствует неразрушенной структуре жидкости, по величине намного больше табличной вязкости. Данный результат наглядно подтверждает, что табличная вязкость относится к жидкости с полностью разрушенной пространственной структурой. Из рисунка можно видеть полную аналогию поведения вязкости обычных жидкостей с поведением вязкости дисперсных систем, обладающих тиксотропными свойствами. Поэтому представляет большой интерес возможность прямого измерения вязкости жидко- стей с неразрушенной равновесной структурой.

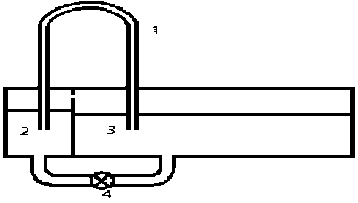
Рис. 3. Принципиальная схема установки для измерения вязкости: 1 – капилляр; 2 и 3 – сосуды с жидкостью; 4 – кран для выравнивания уровней

С этой целью была сконструирована установка по измерению вязкости жидкостей при предельно малых градиентах скорости течения (рис. 3), когда можно было ожидать, что при элементарных актах вязкого течения структура жидкости мало изменяется. Исследуемая жидкость перетекает из сосуда 2 в сосуд 3 по длинному капилляру 1 под действием создаваемой в них разности уровней, причем сечение первого сосуда примерно в 100 раз меньше второго, что позволяет пренебречь изменением уровня во втором сосуде. Кроме того, оба сосуда сообщаются широкой стеклянной трубкой с краном 4, при помощи которого уровни жидкостей в сосудах можно выравнивать. Сосуды герметично закрываются и между собой имеют воздушное сообщение.

Изменение уровня жидкости в малом сосуде измерялось вертикальным катетометром с точностью до 0,1 мкм. Такая точность достигалась увеличением дифракционной картины от границы мениск жидкости – воздух. Отсутствие влияния испарения, а также капиллярных и термоосмотических потоков проверялось по сохранению положения менисков жидкости при отсутствии разности уровней в сосудах.

Установка располагается на специальном фундаменте, изолированном от пола здания, чтобы исключить возможные вибрации установки.

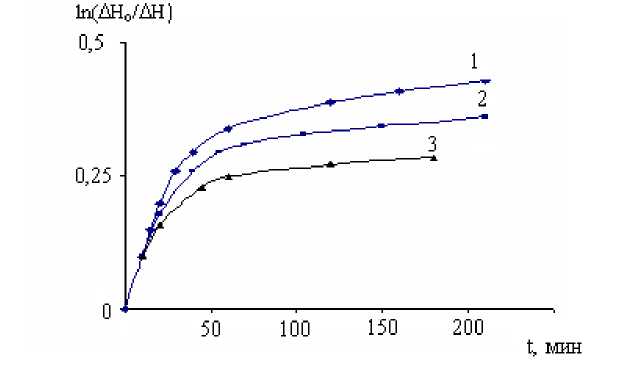
Рис. 4. Зависимость ln( Δ H o / Δ Н ) от времени t для жидкости ПЭС-1 при 1) Δ H 0 = 40 мкм, 2) Δ Н 0 = 35 мкм, 3) Δ Н 0 = 31 мкм

Зависимость между разностью уровней в сосудах и временем, когда исследуемая жидкость перетекает по капилляру из одного сосуда в другой, можно получить, воспользовавшись законом Пуазейля:

π r ² Δ p V = t ^,

8lη где V – объем жидкости, вытекающей из капилляра за время t;

r – радиус капилляра;

l – его длина;

Δ p – движущая разность давлений;

η – вязкость жидкости.

Можно показать, что между разностью уровней Δ H в сосудах и временем t существует следующая зависимость:

_ln Δ H 0 = π r ⁴ ρ g _{t ,                                    (5)}

ΔH    8Slη где ρ – плотность жидкости;

• S – площадь сечения малого сосуда, из которого вытекает жидкость;

Δ H о – начальная разность уровней.

Из выражения (5) следует, что если вязкость жидкости при любой разности давлений или при всех градиентах скорости течения остается постоянной, то зависимость ln ( Δ H o / Δ H) от времени должна быть линейной. Если же при малых градиентах скорости течения вязкость будет повышаться, то соответственно будет наблюдаться отклонение от этой зависимости. Для измерения повышенной вязкости ПЭС-1 использовался капилляр с внутренним диаметром 1,25 мм и длиной 87 см. Площадь сечения малого сосуда составляла 2,5 см².

На рисунке 4 представлены зависимости ln ( Δ H o / Δ H) от времени при разных значениях начальной разности уровней Δ H o для ПЭС-1. Можно видеть, что при больших градиентах скорости течения зависимость линейная. Однако, начиная с определенного значения разности уровней, наблюдается все большее отклонение от линейной зависимости, что свидетельствует о повышении наблюдаемой вязкости, причем при меньших значениях Δ H o отклонение начинается раньше.

Из формулы (5) видно, что вязкость обратно пропорциональна тангенсу угла наклона кривой зависимости ln ( Δ H o / Δ H) от t и для расчета вязкости можно получить выражение:

η = η o ⋅ tg ϕ o _{.                                              (6)}

tg ϕ

Соответствующий расчет вязкости по тангенсу угла наклона кривой дает для ПЭС-1 значение 0,43П, тогда как табличная вязкость равна 0,03П. Вязкость по мере уменьшения градиента скорости течения увеличивается в ∼ 14.3 раза.

Таким образом, исследование показало наличие особой структуры, подобной тиксотропной структуре коллоидных растворов, в жидкостях в условиях, близких к покою. В покое устанавливаются временные связи, приводящие к более упорядоченной структуре с повышенной вязкостью. При механическом воздействии временные зацепления нарушаются, приводя к значениям табличной вязкости, которая относится к жидкости с разрушенной пространственной структурой, соответствующей ламинарному течению жидкостей.

Рассмотренное явление может иметь важное практическое приложение во всех процессах, где преобладают медленные течения, например в грунтоведении и почвоведении, в частности, для объяснения явления морозного пучения грунтов, при процессах фильтрации жидкостей и растворов через искусственные и естественные мембраны.