Исследование вязкоупругих свойств текстильного подвеса в модели парашютной системы для перспективных космических возвращаемых аппаратов

В работе [1] предложен новый тип парашютной системы (ПС) с упругим звеном между парашютом и грузом, груз в которой тандемно разделяется на две части, соединеные гибким тросом. Выбором проектных параметров ПС возможно обеспечить малые динамические перегрузки на верхний груз в полете и при посадке. Для изделий авиационнокосмической техники верхним грузом может служить часть, которая не допускает высоких ударных перегрузок, например, кабина экипажа, а нижним грузом — отработавшие системы и узлы, в сохранении конструкционной целостности которых нет необходимости.

Летные эксперименты [2] показывают, что на этапе разделения и разведения грузов на заданную разность высот динамические перегрузки могут достигать нескольких десятков единиц. Для разработки алгоритма управления процессом разведения грузов, минимизирующего возникающие перегрузки, необходима математическая модель, учитывающая реальные механические свойства троса.

Основной задачей данной работы является получение основных механических характеристик погонной длины троса экспериментальной установки ПС для перспективных космических возвращаемых аппаратов с целью составления математической модели процесса разведения грузов, удовлетворительно согласующейся с опытными данными в части характеристик продольной деформации и максимальных динамических перегрузок.

экспериментальная установка

За основу экспериментальной установки взята материальная часть ПС, использовавшаяся в летном эксперименте, описанном в работе [1]. Для проведения исследования груз m ₁ вместе с механизмом управления длиной троса крепится стационарно на высоте ~5 м от пола (рис. 1). Груз m ₂ массой 4,65 кг подвешивается под ним на тросе.

Разведение грузов осуществляется при помощи механизма управления длиной троса, который представляет собой подпружиненную катушку с тормозом (рис. 2).

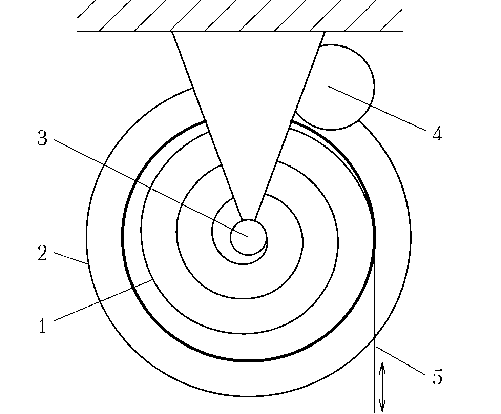
Рис. 2. Конструктивная схема механизма управления длиной троса: 1 — спиральная пружина кручения; 2 — обод катушки; 3 — ось; 4 — тормоз (зажим обода); 5 — трос

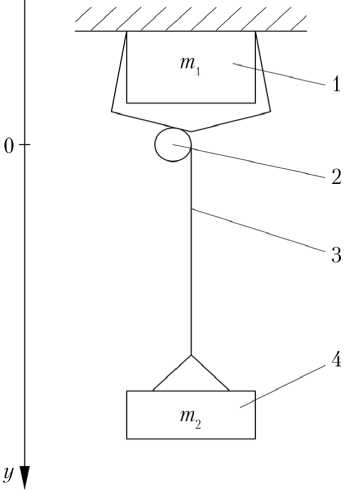
Рис. 1. Схема экспериментальной установки: 1 — груз m₁; 2 — механизм управления длиной троса; 3 — трос;

4 — груз m2

Трос намотан на катушку ∅ 100 мм, которая вращается на оси. Катушка соединена с неподвижной осью спиральной пружиной кручения. При вращении катушки пружина сжимается, создавая крутящий момент в обратную сторону. Имеется возможность прекращать вращение катушки, зажимая ее обод тормозом, работающим по циклограмме, представленной на рис. 3.

В летном эксперименте, описанном в работе [1], при разведении грузов тормоз механизма управления длиной троса работает по циклограмме, представленной на рис. 3.

В интервале времени от 0 до 1,4 с тормоз включен, груз m ₂ висит под грузом m ₁ (см. рис. 1). Далее начинается процесс дискретного опускания груза m ₂ относительно m ₁: тормоз периодически выключается на 0,3 с и включается на 0,2 с в течение 7,5 с.

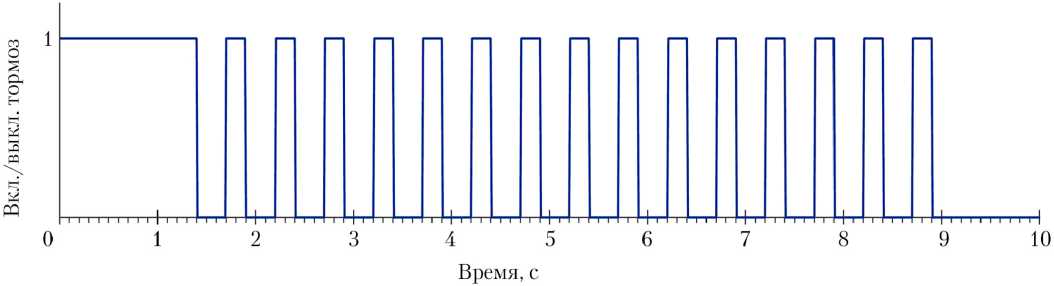
Рис. 3. Циклограмма работы тормоза механизма управления длиной троса: 0 — тормоз выключен; 1 — тормоз включен

Команды электронной системы управления подаются согласно представленной на рис. 3 циклограмме, однако при физической работе исполнительных органов имеется некоторая временная задержка.

В качестве троса применяется полиэфирный шнур ∅ 1,5 мм, сплетенный из 12 нитей. Согласно данным производителя, линейная плотность шнура составляет 2 г/м, разрывная нагрузка — 1 040 Н, высота плетения — 1,6 мм.

результаты стендового эксперимента

Обработка видеозаписи процесса движения [3] позволяет получить зависимость координаты y груза m ₂ от времени. Считаем, что нулевое значение высоты соответствует положению оси катушки (рис. 2). Зависимость динамических перегрузок m ₂ от времени фиксируется при помощи трехосного акселерометра, аналогичного тому, который применялся в работе [2] для фиксации перегрузок m ₁.

Результаты стендового эксперимента (с частотой видеозаписи 60 кадров в секунду) в виде графиков показаны на рис. 4.

Движение груза m2 начинается в момент времени t = 0 c. На графиках показан процесс опускания груза на пяти первых циклах. Далее движение груза m2 уже нельзя считать одномерным, поскольку возрастающие возмущения вызывают пространственное движение груза m2, и погрешность определения вертикальной координаты при помощи видеозаписи существенно возрастает.

Синей кривой на рис. 4 показана зависимость координаты y от времени. В момент времени t = 0 c точка подвеса груза m ₂ находится ниже оси катушки на 0,11 м. Далее начинается движение груза, кривая монотонно возрастает. В момент включения тормоза наблюдается точка перегиба кривой, затем при торможении производная функции координаты уменьшается и на 0,1–0,2 c меняет знак. После выключения тормоза происходит разгон, производная возрастает. Подобный характер движения прослеживается на пяти представленных циклах.

На рис. 4 график скорости получен дифференцированием табличной функции координаты при помощи центрального разностного отношения v = -^+^ + 0 (t2), (1) 2т где V — скорость груза; τ — отрезок времени, за который снимается кадр; yi–1 и yi+1 — координаты груза на следующем и предыдущем кадрах; O(τ2) — остаточный член, характеризующий погрешность аппроксимации.

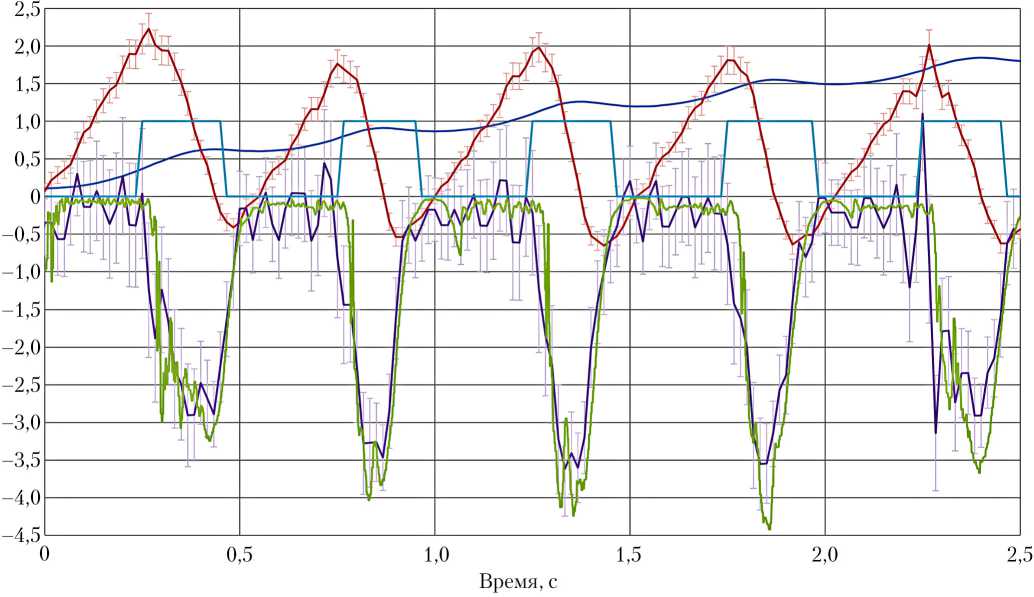
Рис. 4. Параметры движения груза m 2 в стендовом эксперименте: ■ — координата у, м; ■ — скорость, м/с; ■ — перегрузка, g; ■ — перегрузка (акселерометр), g; ■ — тормоз вкл./выкл.

Центральное разностное отношение (1) дает второй порядок точности [4]. График перегрузки n получен тем же способом дифференцирования функции скорости. На кривых рассчитанных скорости и перегрузки показаны планки погрешностей.

Погрешность фиксации координаты груза m ₂ определяется соответствием размера объекта количеству пикселей на видеоизображении. В полученной видеозаписи один пиксель соответствует величине погрешности δ _y = 2,5 мм. При движении объекта его изображение «размазывается», поэтому считаем, что при скорости 2 м/с погрешность определения координаты увеличивается вдвое и составляет величину δ _y = 5 мм. Для промежуточной скорости значение погрешности получаем линейной интерполяцией.

На основе методики обработки результатов экспериментов [5] погрешность вычисления скорости δ _V по формуле (1) определяется выражением

^δ V

^{2 δ y} 2 τ

.

Соответственно, погрешность вычисления перегрузки δ _n оценивается как

δ =   2 δ V n      2gτ

δ

y

2 g τ ^{2 ,}

где g — ускорение свободного падения.

Зеленой кривой на рис. 4 показана суммарная перегрузка, измеренная акселерометром. С учетом диапазона погрешностей, полученные данные хорошо согласуются с вычисленными значениями.

На кривой скорости (рис. 4) видно, что на втором и четвертом циклах минимальная скорость реализуется до момента подачи команды выключения тормоза. Значения модуля минимальной скорости | V _min| в этот момент значительно меньше модуля максимальной скорости | V _max| на рассматриваемом цикле, из чего следует, что колебательный процесс является затухающим.

Из графиков на рис. 4 видно, что при выключенном тормозе и разгоне груза под действием силы тяжести значение модуля перегрузки принимает некоторую величину, которая с каждым циклом возрастает. Это объясняется действием пружины кручения катушки. Усреднив показания перегрузки во время выключенного тормоза, можно оценить силу натяжения троса, вызванную действием пружины. На рис. 5 показаны графики зависимости силы натяжения троса Fпр от длины троса, полученные из перегрузок в стендовом эксперименте (см. рис. 4) и по результатам дополнительно проведенной серии измерений динамометром. При длине вытравленного троса, равной нулю (y = 0 м), сила натяжения Fпр ≈ 3 Н. При вытравливании троса пружина сжимается, увеличивается сила натяжения. Начиная с величины y = 2 м, значение силы остается примерно постоянной и составляет 6–8 Н. Участки несовпадения и немонотонности кривых могут быть вызваны процессами сухого трения в механизме пружины, когда между ее витками и кожухом возникает трение. Для дальнейших расчетных исследований на рис. 5 предлагается модель

1,125 y ² – 4,5 y – 3 (0 ≤ y ≤ 2),

7,5                 ( y > 2).

F пр

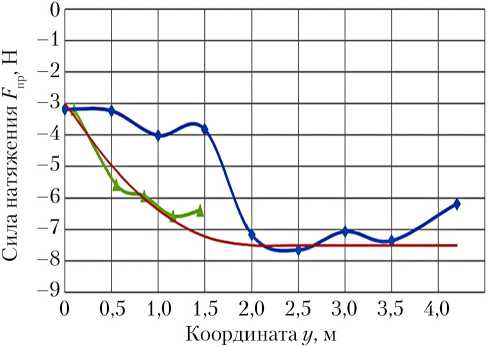
Рис. 5. Зависимость силы натяжения троса под действием пружины кручения катушки: ▲ — стендовый эксперимент; ♦ — измерения динамометром; ■ — модель

модель вязкоупругих деформаций троса

Существует большое количество моделей, описывающих с определенными допущениями поведение материалов при деформациях [6–8]. Самыми простыми из них являются модель упругого тела , подчиняющегося закону Гука, и модель вязкого тела , закон деформирования которого аналогичен закону течения идеальной вязкой жидкости, в которой напряжения пропорциональны скорости деформации.

В более общем случае вязкая составляющая силы может носить степенную зависимость от скорости деформаций [6].

В отдельную группу следует выделить упруго-вязкие модели [7]. В их основе лежит соединение вязкого и упругого элементов.

Одной из моделей, описывающих силы внутреннего трения в материале, является упруго-вязкая модель Кельвина – Фойгта [6], схематически изображенная на рис. 6. Она состоит из параллельно соединенных между собой упругого и вязкого элементов.

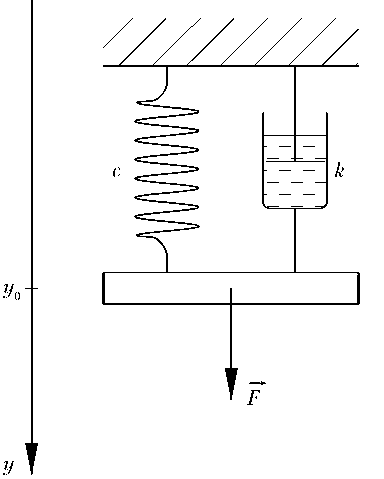
Рис. 6. Модель упруго-вязкого тела Кельвина–Фойгта: F — сила трения; c — коэффициент жесткости; k — коэффициент вязкости.

Таким образом, в модели считается, что силы трения имеют вязкий характер, а напряжения и деформации в простейшем случае одноосного напряженного состояния связаны зависимостью

F = c ( y – y ₀) + k y , dt

где c — коэффициент жесткости; k — коэффициент вязкости. Первое слагаемое в выражении (3) соответствует силе упругости, второе — силе вязкости. В модели (3) принимается допущение, что при растяжении троса нет остаточных деформаций, т. е. удлинение ( y – y ₀) — упругое [7].

Рассматриваемая модель обладает тремя полезными свойствами:

• •    при циклическом деформировании обнаруживается различие между зависимостями напряжения от деформации

при нагружении и разгрузке упруговязкой системы, что соответствует явлению гистерезиса, присущему процессам деформирования реальных тел;

• •    модель описывает свойство ползучести: при постоянной нагрузке с течением времени происходит постепенное увеличение деформации системы;

• •    при рассмотрении свободных колебаний модели Кельвина–Фойгта обнаруживается явление затухания колебаний, качественно сходное с явлением затухания колебаний реальных деформируемых тел.

В текстильном материале внутреннее трение является результатом совокупного действия большого числа малых отдельных сил трения между составными элементами различных масштабов. Модель (3) является весьма приблизительной и не претендует на точное описание процесса деформаций при механическом нагружении троса.

Принимая модель (3), уравнение свободных одномерных колебаний груза, подвешенного на вязкоупругом тросе, имеет вид my.. = mg – c(y – l0) – k y.. (4)

Приняв другие обозначения, уравнение (4) переписывается следующим образом:

y + 2 γ y + ω ₀ ² y = ω ₀ ² l ₀ + g,        (5)

где

2 γ = mk ,

ω

² = ^c

⁰ m ^.

При не слишком значительном вязком сопротивлении ( γ <  ω ₀) решение уравнения (5) имеет вид:

y = ae–γtsin(ωt + ϕ0) + l0 + mcg, где

ω = ω ₀² – γ ² ,

а параметры a и ϕ ₀ определяются из начальных условий задачи колебаний.

анализ результатов стендового эксперимента

Результаты анализа экспериментальных данных (см. рис. 4) приведены в таблице. В первом цикле при торможении груза происходит натяжение троса в бухте на катушке, что вносит неопределенность в описание свободных продольных колебаний, поэтому в таблице первый цикл не представлен. Для каждого цикла (со второго по пятый) определены моменты начала торможения («тормоз вкл.»), максимальной скорости Vmax, нулевой скорости V = 0 м/с и минимальной скорости Vmin. Считаем, что в момент включения тормоза координате y соответствует длина нерастянутого троса l0 на текущем цикле. Промежуток времени между моментами Vmax и V = 0 м/с считаем четвертью периода Т свободных колебаний и находим из него частоту колебаний

2π to = -у—.

Для вычисления коэффициента затухания используем значения скорости V max и Vmin на полупериоде:

Y = ~ In

V max

V min

результаты стендового эксперимента

№ цикла		t , c	y , м	V , м/с	l 0, м	T , c	to , 1/c	Y , 1/c	to 0, 1/c	k , кг/с	c , кг/с2	ES = cl 0, кг·м/с2	f = kl 0, кг·м/с
2	Тормоз вкл.	0,75	0,77	1,73	0,77	0,32	19,63	7,26	20,9	67,5	2 038	1 569	52,0
	V max	0,77	0,8	1,79
	V = 0 м/с	0,85	0,91	0
	V min	0,92	0,89	–0,56
3	Тормоз вкл.	1,25	1,1	1,91	1,1	0,4	15,71	5,42	16,6	50,4	1 284	1 412	55,4
	V max	1,27	1,13	1,98
	V = 0 м/с	1,37	1,26	0
	V min	1,43	1,24	–0,67
4	Тормоз вкл.	1,74	1,39	1,67	1,39	0,4	15,71	5,28	16,6	49,1	1 277	1 775	68,3
	V max	1,77	1,44	1,84
	V = 0 м/с	1,87	1,56	0
	V min	1,93	1,53	–0,64
5	Тормоз вкл.	2,23	1,65	1,59	1,65	0,56	11,22	3,22	11,7	29,9	634	1 045	49,4
	V max	2,26	1,7	1,65
	V = 0 м/с	2,4	1,85	0
	V min	2,47	1,81	–0,67
Результат:												1 450±270	56,3±7,2

Значения для собственной частоты to ₀, коэффициентов вязкости k и жесткости c находим из формул (8), (6) и (7), соответственно.

Из таблицы видно, что при увеличении длины нерастянутого троса l0 с каждым циклом уменьшаются значения k и c. В двух правых колонках приведены величины ES = сl0 и f = kl0, каждая из них принимает близкие значения в каждом цикле. Среднеквадратичное отклонение для ES по четырем циклам составляет 20%, для f — 13%. Численные результаты приведены в последней строке таблицы. Полученные значения можно использовать как параметры в математической модели движения груза на основе уравнения (4). Величины ES и f являются характеристиками используемого вида шнура. Для вычисления значений жесткости и вязкости шнура конкретной (погонной) длины нужно величины ES и f разделить на эту длину.

моделирование процесса опускания груза в стендовом эксперименте

Для моделирования стендового эксперимента рассматривается задача движения груза, подвешенного на вертикальном тросе. Трос стравливается с катушки. Управление движением происходит при помощи фрикционного тормоза, который имеет возможность мгновенно (без проскальзывания) прекращать вращение катушки. Схема модели показана на рис. 7. Груз движется под действием суперпозиции силы тяжести и силы натяжения троса. Тормоз работает с периодом 0,5 с: через 0,3 с от начала цикла подается команда на включение и потом, через 0,2 с, — на выключение (см. рис. 3). При фактической работе тормоза от момента выдачи команды до срабатывания механизма существуют временные задержки.

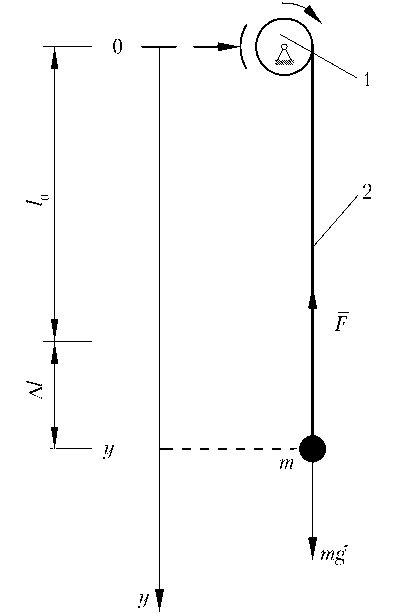
Рис. 7. Схема исследуемой модели: 1 — катушка с фрикционным тормозом; 2 — трос; l₀ — длина нерастянутого троса; Δl — удлинение троса; F — сила натяжения троса

Моделирование процесса движения груза на тросе сводится к последовательному попеременному решению двух независимых задач движения (при выключенном или включенном тормозе). При этом результаты решения одной задачи в конечный момент времени являются начальными условиями для другой.

При выключенном тормозе движение описывается дифференциальным уравнением m y2 = mg – Fпр,          (9)

где F _пр — сила натяжения троса, обусловленная действием пружины кручения, которая задается моделью (2).

При включенном тормозе считаем, что вращение катушки мгновенно останавливается, и движение груза происходит под действием суммы сил тяжести и натяжения троса:

где

m y = mg – F , dt ²

F = ^ES ( y – l ) + ^{f dy} .

• l 0           ⁰       l 0 dt

  
  

Дополнив уравнения (9) и (10) началь ными условиями y = y и = V , 0 dt 0 получаем задачи Коши, которые решаются любым из стандартных способов [4]. На временном интервале с включенным тормозом l0 = y0. Сила натяжения троса в выражении (11) состоит из слагаемых упругой деформации и вязкого трения, величины ES и f были определены экспериментально (см. таблицу).

Математическая модель силы натяжения троса (11) основана на допущении о гармонических свободных колебаниях груза на тросе с экспоненциально затухающей амплитудой.

Численное интегрирование уравнений (9) и (10) проводится методом Верле [9] с шагом τ = 0,01 с. Результаты работы математической модели показаны на рис. 8 в виде графиков координаты y , скорости V и перегрузки n в сравнении с экспериментальными данными.

Анализ графиков рис. 8 показывает, что результаты расчета совпадают с экспериментальными данными с учетом погрешности их определения практически на всех участках моделируемых циклов опускания груза. Рассогласование по координате y не превышает 3%. Следует отметить, что на результаты расчетов существенно влияют модель силы натяжения троса от пружины кручения на катушке и длительность циклов включения/выключения тормоза.

Рассмотрим более подробно расчетные параметры на втором цикле, представленные на рис. 9. Тормоз включается в момент времени 0,78 с. Согласно принятой модели (11), сила натяжения троса F складывается из упругой Fупр и вязкой Fвяз составляющих, их графики представлены на рис. 10. В момент включения тормоза удлинение троса (y – l0) равно нулю, а скорость движения груза V и, соответственно, скорость деформации максимальны. Следовательно, упругая составляющая силы Fупр натяжения троса в начальный момент равна нулю, а вязкая составляющая Fвяз — максимальна. Далее происходит удлинение троса и уменьшение скорости, упругая составляющая Fупр силы натяжения растет, а вязкая составляющая Fвяз уменьшается так, что их сумма F принимает максимальное значение через 0,05 с после включения тормоза. На графиках рис. 9 видно, что форма кривой расчетных перегрузок не совпадает с формой экспериментальных зави- симостей, максимальная перегрузка возникает в момент ~0,08 с от включения тормоза. В момент 0,1 с от включения тормоза скорость груза меняет знак и, следовательно, вязкая составляющая Fвяз также меняет знак. Упругая составляющая Fупр силы натяжения знак не меняет (строго говоря, текстильные материалы не работают на сжатие, и сила натяжения F = 0 Н при y ≤ l0, но в рассматриваемой задаче такой случай не реализуется).

На графике рис. 9 пунктирными кривыми показаны результаты расчетов без учета вязкой составляющей силы натяжения троса (имеется только упругая составляющая F _упр, F _вяз = 0 Н). Форма кривых скорости и перегрузок качественно отличается от результатов расчетов с учетом F _вяз. Максимальное значение перегрузок при этом возросло на 40%. Для выяснения зависимости вязкой составляющей силы натяжения троса от скорости движения груза при отрицательных значениях последней требуются дополнительные исследования.

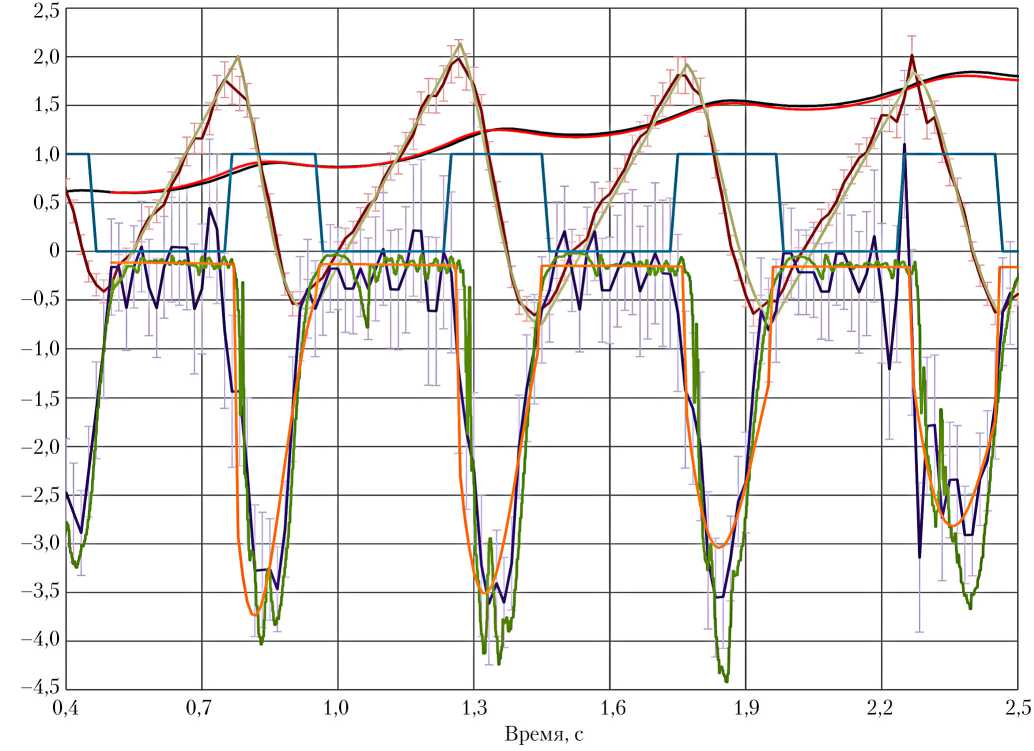
Рис. 8. Сравнение экспериментальных и расчетных данных кинематических и динамических параметров движения груза: ■ — координата у, м; ■ — координата у (расчет), м; ■ — скорость, м/с; ■ — скорость (расчет), м/с; ■ — перегрузка, g;

■ — перегрузка (акселерометр), g; ■ — перегрузка (расчет), g; ■ — тормоз вкл./выкл.

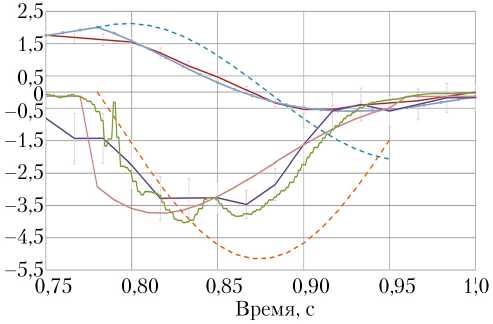
Рис. 9. Параметры движения груза на втором цикле: ■ — скорость V, м/с; ■ — скорость V (расчет), м/с; ■ — скорость V (расчет без учета F_вяз), м/с; ■ — перегрузка п (акселерометр); ■ — перегрузка п;

■ — перегрузка п (рас-чет); ■ — перегрузка п (расчет

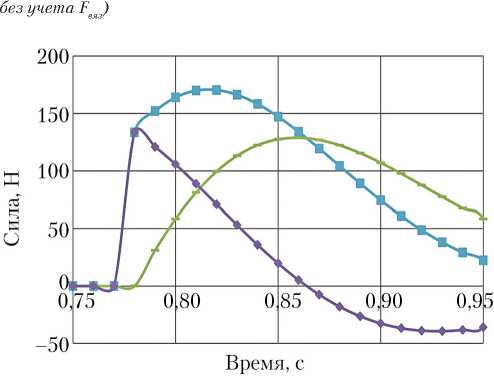
Рис. 10. Компоненты силы натяжения троса расчетной модели на втором цикле: ■ — F = F_упр + F_вяз;

ES

• ■ — F =---( У - l₀ ) ; ■ — F

упр 1            и            вяз f dy l0 dt

выводы

На основе материальной части, использовавшейся в работе [1], построен стенд с экспериментальной установкой для исследования механических характеристик текстильного троса.

В результате стендового эксперимента получены зависимости параметров движения и перегрузки груза от времени.

Из полученных экспериментальных данных определены коэффициенты жесткости и вязкости для погонной длины шнура, исходя из предположения о справедливости упруго-вязкой модели Кель-вина–Фойгта.

Разработана математическая модель одномерного движения груза на вязкоупругом текстильном подвесе в допущении упруго-вязкой модели Кельвина–Фойгта.

Результаты математического моделирования с использованием экспериментально полученных коэффициентов удовлетворительно согласуются с экспериментом в части значений деформаций и максимальной перегрузки.