Исследование влияния анизотропии поверхностного пластического упрочнения на распределение остаточных напряжений в полых и сплошных цилиндрических образцах

PNRPU MECHANICS BULLETIN

For the calculation of residual stresses and plastic strains in hollow and solid surface-hardened cylindrical specimens we suggest the mathematical models, which take into account both the cases of hardening leading to the isotropy (hydraulic shot blasting procedure) and to the anisotropy (roller burnishing process) of plastic strains in the surface layer. The introduced mathematical model has a hardening anisotropy parameter which ties the axial and circumferential components of the residual plastic strains tensor. We use the determined axial and/or circumferential components of the residual stresses tensor as the input information. Also we use the following assumptions: smallness of the off-diagonal elements of the residual plastic strains tensor and residual stresses tensor, plastic incompressibility of material, absence of the secondary plastic strains of the material in the compression area of the surface layer. The boundary value problems of the hardened layer stress-strain state estimation after the hardening for the hollow and solid cylindrical specimens are solved and the solution is given in the paper. We give the method for the mathematical model parameter identification under the condition of selfequilibrated residual stresses and the method for the experimental determination of residual stresses by the circles and strips approach. Also, the cycle of the hardening experiments for the hollow and solid specimens from the 40Kh steel (having different proportions of internal and outer diameters) in the roller burnishing process and hydraulic shot blasting modes was performed with the determination of the residual stresses. The mathematical model adequacy is verified through the comparisons with experimental data; good agreement of the calculated and experimental data is demonstrated. The calculated numerical values of the hardening anisotropy parameter are given. The fact that the procedure of surface anisotropic hardening (roller burnishing process) leads to the strong layering of the epures of axial and circumferential residual stresses in depth of the hardened layer is established. Contrastingly, the case of the isotropic hardening (hydraulic shot blasting) leads to almost coinciding epures. Using the experimental and calculated data we have shown that the hardening of tool roller type leads to the larger absolute values of the compressing stresses, which by more than 30% exceeds the stresses after the hardening of hydraulic shot blasting type for the specimens of the same geometry. For the main results of the research we have given the necessary data in the table and also we have presented the epures for the residual stresses distribution.

Наряду с металлофизическими подходами к улучшению прочностных свойств металлов и конструкторскими методами улучшения надежности элементов конструкций важную роль играют и технологические способы повышения характеристик износостойкости, прочности и сопротивления усталости на основе методов поверхностного пластического деформирования [1–8 и др.]. При этом положительный эффект от поверхностного пластического деформирования обусловлен главным образом за счет возникновения сжимающих остаточных напряжений в тонком поверхностно упрочненном слое детали, которые замедляют или вообще блокируют эволюцию (выход на поверхность) различного рода вакансий и дислокаций в процессе эксплуатации изделия. Число работ в области разработки феноменологических методов оценки остаточных напряжений и их влияния на физико-механические характеристики, повышающих показатели надежности, необозримо, но подавляющее их большинство связано с сугубо экспериментальными подходами, позволяющими определить одну или две компоненты тензора остаточных напряжений [9–15 и др.].

В работах [16, 17] рассмотрены подходы для определения трехосных полей остаточных напряжений, однако предложенные методы практически неразрешимы на техническом уровне. Кроме того, математическое разрешение проблемы определения остаточных напряжений в этих методах приводит к необходимости решения плохо обусловленных обратных задач. Существующие численные и численно-аналитические методы можно применять только в случае, если они сводятся либо к классической контактной упругопластической задаче [18–21], либо к задаче термоупругопластичности [22–27]. Применение аналогичных подходов к математическому моделированию методов поверхностного пластического деформирования, основанных на ударном (динамическом) взаимодействии инструмента с поверхностью деталей (обработка дробью, виброударная, центробежноударная обработка и др.) и квазистатическом взаимодействии деформирующего элемента (шарики, ролики и др.) с обрабатываемой поверхностью по схемам качения, скольжения или внедрения, крайне затруднительно в силу сложности учета всех технологических параметров процедуры упрочнения. Это связано с тем, что и при динамическом, и квазиста-тическом процессах упрочнения деформирующий элемент упорядоченно или хаотично оставляет на поверхности большое число локальных пластических отпечатков, которые в результате покрывают всю поверхность детали. Размеры очага пластической деформации зависят от материала детали, размера и формы инструмента, от энергии удара по поверхности и многих других (в основном случайных) факторов.

Математическое описание кинетики упрочненных конструкций в силовом поле внешних нагрузок приводит к постановке краевых задач с начальным напряженно-деформированным состоянием, сформированным после процедуры поверхностного пластического упрочнения. Для решения таких задач необходимо иметь полную информацию о тензорах остаточных напряжений и пластических деформаций по всему объему интегрирования. В работах [28, 29] разработан расчетно-экспериментальный метод определения компонент тензоров остаточных напряжений и пластических деформаций в сплошном цилиндрическом образце по экспериментально определенной окружной компоненте тензора остаточных напряжений в поверхностно упрочненном слое (задача решается в стандартной цилиндрической системе координат r , 0 , z ), при этом недиагональными компонентами тензоров напряжений и деформаций авторы пренебрегали. При решении поставленной задачи в [28, 29] использован ряд гипотез, одна из которых следующая: характер распределения пластических деформаций по глубине упрочненного слоя цилиндрического образца такой же, как и при упрочнении полупространства, что математически означает выполнение равенства q_z ( r ) = q ₀ ( r ) (здесь q_z ( r ) и q ₀ ( r ) - осевая и окружная компонента остаточных пластических деформаций). В дальнейшем будем говорить, что технологии упрочнения (пневмо- и гидродробеструйная обработка, обработка микрошариками, термопластическое упрочнение), соответствующие этой гипотезе, относятся к изотропному упрочнению поверхности в направлениях осей z и 0 .

Существующие экспериментальные данные [12, 13] и расчеты, выполненные в [28, 29], показывают, что при изотропном упрочнении эпюры осевой и окружной компонент остаточных напряжений в области упрочненного слоя у сплошных цилиндрических образцов практически совпадают. Однако для ряда упрочняющих обработок, например таких как обкатка роликом, алмазное выглаживание и др., величины экспериментальных осевых и окружных компонент остаточных напряжений в слое существенно различаются, и методика [28, 29] требует модификации. Попытка обобщения и уточнения модели [28,

• 29] предпринята в работах [30–32], в которых введен параметр анизотропии упрочнения a , учитывающий анизотропность распределения полей остаточных пластических деформаций соотношением

qz = a q 0, 0 < a < г, (1)

причем при a ^ 1 наблюдается существенное «расслоение» расчетных диаграмм осевых и окружных компонент остаточных напряжений в упрочненном слое.

В работе [33] методика работ [28–32] обобщена на поверхностно упрочненные полые цилиндрические образцы. Однако в [28–33] не были выполнены детальные теоретические и экспериментальные исследования влияния параметра анизотропии поверхностного пластического упрочнения на напряженно-деформированное состояние упрочненного слоя сплошных и полых цилиндрических образцов, что и является целью настоящей работы.

1.    Методика оценки напряженно-деформированного состояния в упрочненном слое сплошного цилиндрического образца

Приведем основные формулы для расчета остаточных напряжений и пластических деформаций, полученные для самого общего случая анизотропии упрочнения в [30–32], не вдаваясь в детальные подробности их вывода.

Вводится стандартная цилиндрическая система координат, через a i = a i ( r ) и q i = q i ( r) (i = r , 0 , z ) обозначим радиальные, окружные и осевые компоненты тензора остаточных напряжений и пластических деформаций соответственно (недиагональными компонентами этих тензоров пренебрегаем в силу их малости).

Будем считать, что после упрочнения известны величина a в соотношении (1) и полное распределение окружной компоненты остаточных напряжений a0 = a0 (r) (0 < r < R , R - радиус образца). Из уравнений равновесия d a

• ^r~T ^{+ a} r =^a 0 , dr

совместности деформации для полных деформаций г i = e i + q i ( e i - тензор упругих деформаций)

d £fl

r -"Г + г0=г r , dr условия пластической несжимаемости qr+q 0+qz = 0,                                     (4)

закона Гука ei

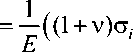
-VCT o ) , i = r , 0 , z ,

где a ₀ =a _r +g₀+c _z ; E - модуль Юнга; V - коэффициент Пуассона для рассматриваемого материала, и гипотезы (1) можно выразить все компоненты напряженно-деформированного состояния упрочненного цилиндра через величины a и а₀ [30-32]:

1r o r(r) = -fo9 (-) d -, 0 < r < R, r 0

, .   (1 + v )(1 — 2 v )

qa ( r ) = "---~—i—- r

9       (1 + av)2 E

—

2+a r 1+a—av

^ J-      (or (9) + (1 + a)09 (9)) d - +

1 + v

+--

(1 + av ) E

(vor(r ) — (1 — у)о9 (r)), qz (r) = a q 9 (r),  qr(r) = — q 9 (r )(1 + a), s0 = 25R - qz(9—-v

R 0 L EJ o 0 (r) = E <80 — qz (r)) + v (or(r) + 09 (r)).

Из уравнения равновесия (2) и условия o_r (R) = 0, которое означает, что упрочненный цилиндрический образец находится в естественном ненагруженном состоянии, получаем

RR

J o9 (r) dr =J d (ro r (r)) = 0, 00

т. е. эпюра напряжений o₉ = o₉(r) является самоуравновешенной.

2.    Методика идентификации параметров математической модели

Для реализации расчетной схемы (6)-(10) необходимо, чтобы величина o₉(r) была известна по всему радиусу образца, но экспериментально ее можно определить только в тонком упрочненном слое (области сжатия) [9-13], поэтому данные для o₉(r) необходимо экстраполировать в область растяжения, но так, чтобы не нарушалось условие са-моуравновешенности (11). Для этой цели используется следующая аналитическая аппроксимация компоненты o₉(r):

o₉(r) = o₀— o1 exp(—(R — h * — r)²/ b²), 0 < r< R, (12) где h* = R — r * - глубина слоя, при которой компонента o₉(r) принимает свой минимум; o₀, o1 и b - параметры, подлежащие определению; она теоретически обоснована и экспериментально подтверждена в работах [28-32].

Рассмотрим алгоритм определения параметров o0, o1 и b в (12) в предположении, что известна экспериментальная информация для компоненты o9 (r) в области сжатия и задан параметр анизотропии a в (1). Используя условие самоуравновешенности (11) для окружной компоненты o9 (r) и условия o9 (r *) = o*, o9 (r0) = 0, (13)

где а * - экспериментальное значение минимума величины a_Q(r), которое достигается в точке r = r*, а r₀ - значение радиуса, при котором значение окружной компоненты обращается в нуль, с учетом (12) получаем систему трех нелинейных уравнений относительно а₀, а1 и b , численное решение которой не вызывает принципиальных трудностей.

Таким образом, методику определения полей остаточных напряжений и пластических деформаций при известных а и экспериментальной зависимости q_q = a_Q(r) можно представить следующей схемой (над стрелками указаны формулы, по которым определяются соответствующие величины):

R, r), r*, а * —(i¹)^-1^ ао, а_рb ⁽¹²⁾> Qq (r) ⁽⁶⁾> аr (r)

(7) > qq (r) (8) > Qr, qz (9),(10) > qz(rX при этом в схеме (14) под вычислением aQ = qq (r) подразумевается аналитическая аппроксимация этой зависимости по формуле (12).

Однако на практике величина а в соотношении (1) неизвестна, и ее можно определить лишь после проведения экспериментальных исследований. В этом случае схема (14) существенно изменяется, и в качестве исходной экспериментальной информации необходимо иметь зависимости a_Q(r) и а_z (r) по толщине упрочненного слоя, а параметр а подлежит процедуре идентификации. Здесь задача сводится к поисковому методу оптимизации: целенаправленно варьируются параметры r₀, r *, а *, которые, в свою очередь, варьируют параметры аппроксимации (12), и а , и для каждой такой совокупности значений этих параметров осуществляется численный расчет по схеме (14) до достижения минимума функционала:

A_q + A_z > min;

А =

।

Л.               .2 12

Е(^аi^(rk)^-аi⁽г)) k=1___________________________

Л

Е(а i(rk))

k=1                     _

i = Q, z,

где Ai - функционал нормированного среднеквадратического отклонения расчетных значений аi (rk ) от соответствующих экспериментальных значений аi (rk); N - число точек дискретизации радиуса r_k в упрочненном слое, в которых известны экспериментальные и расчетные значения окружной и осевой компонент остаточных напряжений.

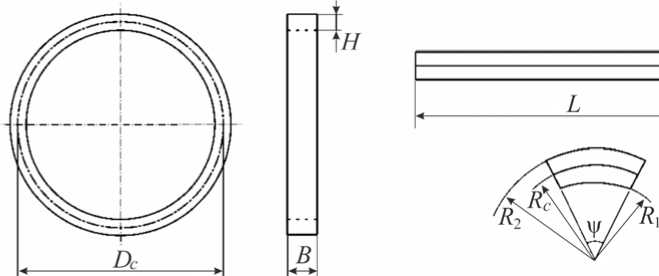
3.    Методика оценки напряженно-деформированного состояния в упрочненном слое полого цилиндрического образца

Рассмотрим полый цилиндр с внешним радиусом R₂ и внутренним R, внешняя поверхность которого подверглась процедуре упрочнения. Схема решения задачи о напряженно-деформированном состоянии в полом цилиндре аналогична схеме (14) для сплошного цилиндра и изложена в работе [33]. Основные расчетные формулы имеют следующий вид:

q 9^(R) =

1 f

° R^(r) = ~J°9 ^(Q)d^QR1 ^ ^R ^ R 2, R

(1 + v)(1 - 2v)

—:----R

(1 + av)²E

2+a r 1+a-av

l+av J 5 +av (оr (Q + (1 + a)a„ (Q)) d« +

R1

+ n 1 + \F(V° R (R) - (1 - v)°9 (R)) , (1 + av) E

qz^(R) = ^aq9^(RX Qr^(R) = ^-q9^{(R)(1 + a)},

s0

___2

RT-

R2²Г           V z

-2 J5 Qz (2)--(° R (Q) + °9 (5) ) dQ,

^R1 R1 L        E                 J

° z(R) = E (^ - q(R)) + v (° R(R) + °9(R)) •

Основные изменения касаются граничных условий для компоненты о_R (r):

° r (R1) = о r (R 2) = 0,

условия самоуравновешенности

R 2

J о9 (R)dR = 0

R1

и аппроксимации экспериментальной зависимости для о₉(r)

°9 ^(R) = °0 ^-°1^eXp V

- h * - r

b

(R - R1),

которая теоретически обоснована и экспериментально подтверждена в работе [33].

Методика определения параметров о₀, °1 и b аппроксимации (17) аналогична соответствующей методике для сплошного цилиндра, т. е. используются характерные точки эпюры: h* = R₂- r * - расстояние от упрочненной поверхности, при котором экспериментальная компонента о₉(r) принимает свой минимум о* = о₉(r*); координата r₀ , для которой выполняется условие о₉(r₀) = 0 и условие самоуравновешенности (16).

Таким образом, схема определения полей остаточных напряжений и пластических деформаций (точнее последовательность их вычисления) будет полностью аналогична схеме для сплошного цилиндра (14).

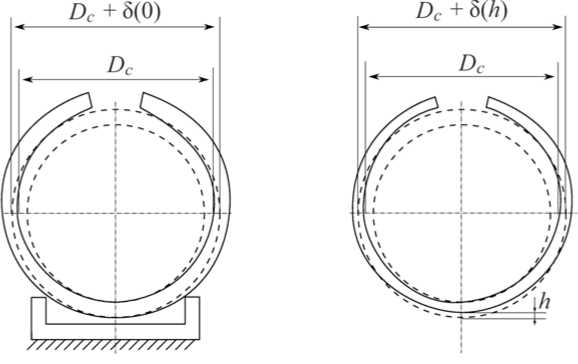
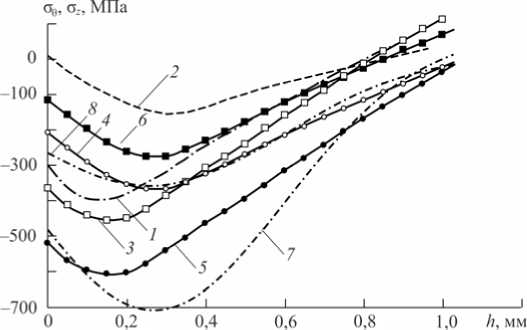
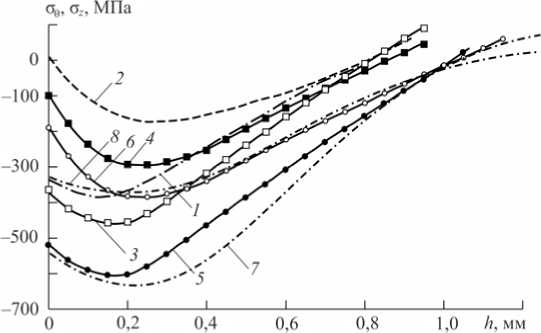
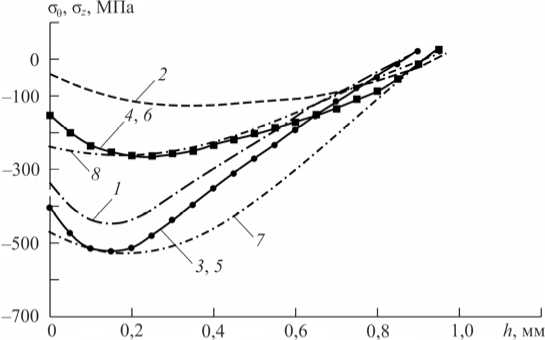
4.    Упрочнение и экспериментальное определение остаточных напряжений в сплошных и полых цилиндрических образцах

Поскольку целью работы является детальное исследование влияния анизотропии поверхностного пластического упрочнения на напряженно-деформированное состояние сплошных и полых цилиндрических изделий, выполнено комплексное экспериментальное исследование для сплошных цилиндрических образцов из стали 40Х диаметром D = 25 мм и полых образцов с различными значениями внешнего и внутреннего диаметров D2/ D1 (25/10 и 25/19 мм) при двух технологиях упрочнения: обкатка роликом (соответствует процедуре анизотропного упрочнения) и гидродробеструйная обработка (соответствует изотропному упрочнению). Для каждого режима упрочнения и каждого варианта геометрических параметров образцов использовались образцы в количестве 5 штук из одной серии (поставки). Обкатка роликом (диаметр ролика 60 мм, профильный радиус 1,6 мм) для всех типов образцов осуществлялась с усилием накатывания 1 Кн при подаче 0,11 мм/об и скорости вращения образца 400 об/мин. При гидродробеструйной обработке поверхность образцов обрабатывалась в течение 8 мин стальными шариками диаметром 2 мм вместе с маслом при давлении 0,28 МПа.

Остаточные напряжений после процедуры упрочнения определялись по методу колец и полосок [10–13, 32, 36], для чего сплошные образцы предварительно рассверливались и растачивались до втулок с внутренним диаметром D₁= 20,15 мм; полые цилиндрические образцы с диаметрами 25/10 мм растачивались до внутреннего диаметра D₁= 20,12 мм; к образцам с диаметрами 25/19 мм процедуры рассверливания и растачивания не применялись.

Дополнительные окружные σˆ _θи осевые σˆ z напряжения, вызванные рассверливанием и растачиванием образцов, определялись по формулам [10–13, 32]

σˆ_θ= E(εˆ_θ+νεˆ_z),σˆ_z= E(εˆ_z+νεˆ_θ), (18) 1-ν2 1-ν2

где εˆ_θ, εˆz – деформации цилиндрического образца на внешней поверхности в осевом и окружном направлении, образовавшиеся в результате расточки и измеренные тензоре-зисторами; E =2⋅105 МПа, ν=0.3 . Экспериментальные значения εˆ_θи εˆz после расточки образцов для технологий обкатки роликом (ОР) и гидродробеструйной обработки (ГДО), а также дополнительные напряжения σˆ _θ, σˆ z , рассчитанные по формулам (18), для сплошных ( D₂/D₁= 25/0) и полых ( D₂/D₁= 25/10) образцов приведены в табл. 1.

Таблица 1

Значения деформаций и напряжений после процедуры рассверливания и растачивания

Режим упрочнения	D2/ D1	εˆθ⋅105	εˆz ⋅105	σˆθ, МПа	σˆ z , МПа
ОР	25/0	26,0	62,5	98,35	154,51
	25/10	22,5	62,0	90,33	151,10
ГДО	25/0	20,0	27,0	61,76	72,53
	25/10	15,0	17,0	44,18	47,25

Из полученных в результате расточки втулок с внутренним диаметром D1*= 20,15 мм и внешним D2 = 25 мм, полученных из сплошных образцов, и втулок с диаметром D1*= 20,12 мм, D2 = 25 мм, полученных из полых образцов, вырезали коль- ца шириной B = 10 мм и толщиной стенки H = (D2 - D1*)/ 2 (для каждого варианта из табл. 1 использовалось 2 втулки на 10 колец) и полоски вдоль образующей втулки длиной L = 30 мм, которые вырезали в пределах центрального угла у = 26° поперечного кольцевого сечения образца (для каждого варианта табл. 1 использовано 3 втулки на 27 полосок, рис. 1). Для образцов с первоначальными размерами D2/ D1 = 25/19 кольца и полоски вырезались без расточки образца в том же самом количестве. Сразу после вырезки у полосок измеряли прогиб f (0) (как показано на рис. 2, а), а у колец после разрезки – изменение диаметра (рис. 3, а).

а                                  б

Рис. 1. Кольцо (а) и полоска (б), вырезанные из втулки

Далее электрохимическим полированием производилось удаление слоев колец, что привело к изменению диаметра 5(h) (рис. 3, б). При удалении слоев полосок измерялись их прогибы f (h) по схеме, представленной на рис. 2, б. Отметим, что здесь f (h) (так же как и 5(h)) отсчитываются от состояния полоски (кольца) до вырезки из втулки. На рис. 2 и 3 полоска и кольцо до вырезки из втулки изображены штриховой линией.

Комбинации остаточных окружных ст₀и осевых стz напряжений втулки в полосках стn(h) и кольцах стk(h) определялись по формулам [10-13, 32]

^СТk^(h ) = ^СТ0 ^(h) ^-Н^стz^(h) = ²

E5(0)Г H

DC I 2

-

-

1E(H - h)²d5(h)

3    D_c²     dh

+

4 E (H - h ) 3Dc²

5( h)

-

2E

3D_c²

J 5(5)d5,

^CTn (^h) = ^CTz^(h ) ^-Ц^ст0 ^(h)

8E

L²R2(2R2 sin У - R_cу)

.f (h) dM+1 (0) dfih) dh dh

где D_c = (D1 + D₂) / 2 - средний диаметр кольца; h - расстояние от наружной поверхности втулки до слоя, в котором вычисляли остаточное напряжение; R₂ , R₁ – наружный и внутренний радиусы цилиндрической полоски;

Rc

4sin у R2 - R3 3у R₂²- R1²

– радиус центра тяжести поперечного сечения цилиндрической полоски;

I(h) '"s¹^ [(R2 - h)4

8sin V [⁽R2 - h)3 - R13 ] V    (R2 - h)²- R1

– момент инерции поперечного сечения полоски относительно нейтральной оси.

а                                       б

Рис. 2. Схема измерения прогиба полоски: а – после вырезки; б – после вырезки и удаления слоя толщиной h

Рис. 3. Схема измерения премещений кольца: а – после разрезки; б – после разрезки и удаления слоя толщиной h

В качестве примера на рис. 4 (эпюры 1 и 2) приведены комбинации осевых и окружных напряжений втулки в полосках оn (h) и кольцах оk (h), вычисленные по зависимостям (19) и (20), для режима обкатки роликом.

Формулы для определения осевых оz (h) и окружных о₀(h) остаточных напряжений втулки получаются из решения системы двух линейных уравнений (19), (20) относительно этих напряжений при известных оn (h), оk (h) и принимают вид

⁰z^(h) = 1—^2 [^оn^(h) ⁺ ^’° k^(h )1,^о0 ^(h) = 1—^2 [° k^(h) ⁺ ^° n^(h)]. ⁽²¹⁾

a

б

в

Рис. 4. Осевые и окружные напряжения во втулках, полосках, сплошном (а) и полом (б, в) цилиндрических образцах из стали 40Х после обкатки роликом: а - D₂ / D1 = 25 / 0;

б - D₂/ D1 = 25/10; в - D₂/ D1 = 25/19; 1 - стn (h); 2 - стk (h); 3 - ст_z (h); 4 - ст₉(h),

5 - стz (h); 6 - ст₀(h); 7 - аппроксимация ст₀(h); 8 - расчет ст_z (h)

Распределение осевых σz и окружных σ_θостаточных напряжений втулки, определенных по формулам (21) для режимов обкатки роликом, представлено на рис. 4 (эпюры 3 и 4). Окончательные формулы для определения окружных σ_θ(h) и осевых σz (h) остаточных напряжений сплошных цилиндрических образцов имеют вид

σ_θ(h)=σ_θ(h)-σˆ_θ, σ_z(h)=σ_z(h)-σˆ_z,

где σˆ _θи σˆz определяются по зависимостям (18), а σ_θ(h) и σz (h) – по (21).

Вычисленные по формулам (22), (18), (21) «экспериментальные» (если быть точным – расчетно-экспериментальные) остаточные напряжения σ_θ(h) и σz (h) по толщине упрочненного слоя h после процедуры упрочнения обкаткой роликом для сплошных образцов приведены на рис. 4, а, а для полых образцов – на рис. 4, б и в (эпюры 5 и 6). Следует отметить, что для полых образцов с D₂/D₁= 25/19 (рис. 4, в) расточка и рассверливание не выполнялись, поэтому σˆ_θ =σˆz =0 и из (22) следует σ_θ(h)=σ_θ(h), σz(h)=σz(h).

Аналогичные расчетно-экспериментальные исследования были выполнены для сплошных и полых цилиндрических образцов, упрочненных по технологии гидродробе-струйной обработки. Поэтапная детализация расчета остаточных напряжений здесь не приводится, а на рис. 5 представлены лишь окончательные «экспериментальные» данные для σz (h) (сплошные линии). Зависимость для σ_θ(h) на рис. 5 не представлена, так как для гидродробеструйной обработки, которая приводит к изотропному упрочнению поверхности (в соотношениях (1) величина α = 1), величины σ_θ(h) и σz (h) практически совпадают.

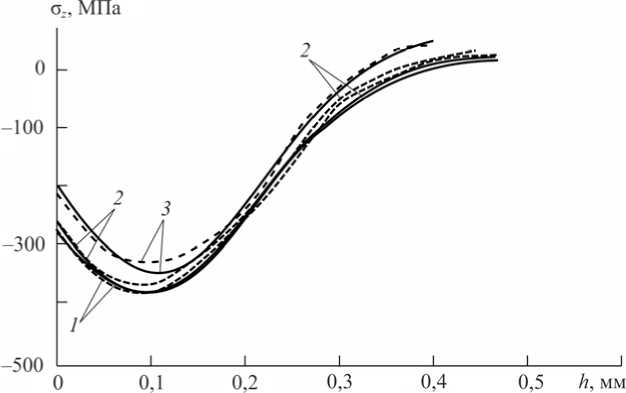
5.    Результаты расчетов и анализ результатов

Для количественной оценки величины анизотропии поверхностного упрочнения при обкатке роликом (ОР) согласно методике для сплошных и полых образцов использовались эпюры 5 и 6 на рис. 4 для σ_θ(h) и σz (h). Параметры аппроксимации компоненты остаточных напряжений σ_θ(h) для сплошных (формула (12)) и полых (формула (17)) упрочненных образцов приведены в табл. 2. Здесь же приведены значения погрешностей расчетных данных для компонент σ_θ(h) и σz(h) по отношению к экспериментальным данным, вычисленные на основании (15), а также численные значения параметра анизотропии α . На рис. 4 для сплошного и полых цилиндров приведены определенные экспериментально (линии 5 и 6) и рассчитанные по приведенным выше методикам теоретические (линии 7, 8) остаточные напряжения σ_θ(h) и σz (h).

При гидродробеструйной обработке (ГДО) экспериментальные зависимости для σ_θ(h) и σz (h) практически совпадают, что также отражается теоретическими моделями и для сплошных, и для полых образцов при коэффициенте α = 1. В табл. 2 приведены параметры аппроксимаций (12) и (17) и погрешность Δ_z отклонения расчетных данных от экспериментальных для компоненты σz (h), а на рис. 5 представлены экспериментальные (штриховые линии) и расчетные (сплошные линии) значения для σz (h).

Рис. 5. Осевые остаточные напряжения в сплошных и полых цилиндрических образцах из стали 40Х после гидродробеструйной обработки: 1 – D₂/D₁= 25/0;

2 – D₂/D₁= 25/10; 3 – D₂/D₁= 25/19; штриховые линии – эксперимент, сплошные линии – расчет

Таблица 2

Значения параметров аппроксимации окружной компоненты σ_θ(h)

Режим упрочнения	D2/D1	σ0 , МПа	σ1 , МПа	b, мм	h* , мм	Δz, %	Δθ, %	α
ОР	25/0	19,95	376,2	0,48	0,275	19,14	8,24	7
	25/10	12,10	61,7	0,64	0,24	11,6	15,9	4
	25/19	110,12	204,3	0,87	0,24	19,4	15,4	6
ГДО	25/0	7,45	390,7	0,38	0,1	3,65	–	1
	25/10	3,44	55,2	0,168	0,1	3,1	–	1
	25/19	21,96	143,7	0,164	0,1	4,12	–	1

Анализ данных табл. 2 свидетельствует о том, что при гидродробеструйной обработке погрешность Δz составляет не более 4 % (как указано выше, σ_θ(h) и σz (h) здесь практически совпадают), при обкатке роликом, когда наблюдается существенное расслоение эпюр σ_θ(h) и σz(h), которое описывается параметром анизотропии α≠1, погрешность Δ_θи Δ_z существенно возрастает до 15–19 %. Снижение погрешности Δ_θ и Δz в этом случае возможно за счет введения функции α = α(r), но это не является целью настоящей работы.

Анализ эпюр на рис. 4 и 5 позволяет сделать следующие выводы:

• 1)    минимальное значение остаточных напряжений и при обкатке роликом, и при гидро-дробеструйной обработке находится не на поверхности детали, а в подповерхностном слое;

• 2)    глубина залегания сжимающих остаточных напряжений σ_θ(h) и σz (h) при обкатке роликом составляет величину до 1 мм, в то время как при гидродробеструйной обработке – около 350 мкм;

• 3)    при обкатке роликом величина максимального (по модулю) остаточного напряжения почти на 30 % больше, чем при гидродробеструйном упрочнении;

• 4)    при обкатке роликом наблюдается существенное расслоение эпюр напряжения σ_θ(h) и σz(h), вызванное анизотропным характером упрочнения поверхности образцов, в отличие от процедуры гидродробеструйной обработки, где они практически совпадают;

• 5)    величина сжимающих напряжений в сплошном образце по модулю больше, чем в полых образцах, при обеих технологиях.

В заключение отметим, что упрочняющие технологии широко применяются в различных отраслях промышленности для повышения ресурса изделия. Однако оценка устойчивости наведенных остаточных напряжений к внешним силовым и температурным воздействиям сводится к решению соответствующих краевых задач с заданным начальным напряженно-деформированным состоянием (после процедуры упрочнения), методика расчета которого представлена в данной работе. Эффективность решения данного класса краевых задач продемонстрирована в публикациях [34, 35], где выполнен расчет кинетики полей остаточных напряжений вследствие ползучести для сплошного цилиндрического образца и лопатки газотурбинного двигателя, но лишь для процедуры изотропного упрочнения изделий.

Результаты настоящей работы свидетельствуют, что неучет параметра анизотропии упрочнения α при решении краевых задач типа [34, 35] может привести к существенным погрешностям расчета.

Работа выполнена при поддержке РФФИ (проект № 13–01–00699–a) и при поддержке Минобрнауки России в рамках базовой части государственного задания ФГБОУ ВПО «СамГТУ» (код проекта: 1151).