Исследование влияния факторов на удельное давление при валковом отжиме кожи
Автор: Ш.Р. Хуррамов, К.К. Тургунов
Журнал: Современные инновации, системы и технологии.
Рубрика: Прикладные вопросы и задачи применения систем и технологий
Статья в выпуске: 2 (4), 2022 года.
Бесплатный доступ
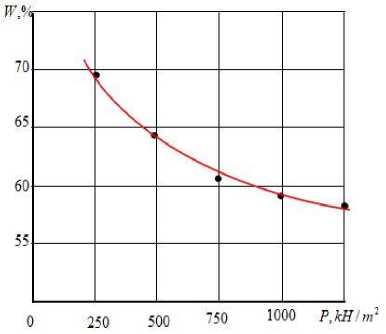
В работе выполнен анализ влияния факторов на удельное давление при валковом отжиме кожи. В результате экспериментальных исследований определены графики зависимостей и получена математическая модель. Выявлено, что параметр технологического удельного давления на кожу в зоне контакта возрастает с увеличением интенсивности нагрузки, скорости валка и ширины площадки контакта, а также с уменьшением радиуса валка. Найдена аналитическая зависимость остаточной влажности кожи от удельного давления. Установлено, что с ростом удельного давления остаточная влажность кожи уменьшается и асимптотически приближается к определенной величине.
Кожа, валковый отжим, удельное давление, ширина площадки контакта
Короткий адрес: https://sciup.org/14124344
IDR: 14124344 | УДК: 677.057 | DOI: 10.47813/2782-2818-2022-2-4-0101-0111
Текст статьи Исследование влияния факторов на удельное давление при валковом отжиме кожи
DOI:
Механическая обработка натуральных кож характеризуется наличием большого количества процессов, выполняемых в валковых машинах. Среди них особую группу составляет валковый отжим кожевенного полуфабриката после дубления (кожи), который является важным для последующих операций двоения и строгания [1,2].
Параметр удельного давления является определяющим для достижения заданного технологического эффекта отжима кожи. Этот параметр характеризуется величиной линейного давления, отнесенной к ширине площадки контакта валков. Поэтому параметры валковых машин сказываются, прежде всего, на величинах ширины площадки контакта валков, а через него на удельном давлении и технологическом эффекте.
Ширина площадки контакта в зависимости параметров валковых машин может быть определена либо теоретически с помощью математического моделирования процесса валкового отжима, либо экспериментально в результате изучения влияния основных параметров валкового отжима кожи на неё.
Математическому моделированию процесса валкового отжима посвящены работы [3-10]. В них на основе моделирования формы кривых контакта валков и закономерности распределения контактных напряжений определены аналитические выражения, описывающие площадку контакта валков и удельное давление.
Работа [11] посвящена экспериментальному исследованию и описанию регрессионной модели ширины площадки контакта. Однако при проектировании отжимных машин для инженерных расчетов требуются более простые зависимости, чем регрессионные. Исходя из этого, в работе поставлена задача на основе результатов работы [11] выполнить описание ширины площадки контакта и удельного давления с помощью эмпирической функции основных параметров валкового отжима кожи.
МАТЕРИАЛЫ И МЕТОДЫ
Ранее была экспериментально исследована ширина площадки контакта валкового отжима кожи в зависимости от интенсивности нагрузки Q , радиуса валка R и скорости валка V [11]. Однако, как свидетельствуют авторы работ [1, 12], остаточная влажность при валковом отжиме определяется не линейным давлением (интенсивностью нагрузки), а удельным давлением, которое определяется как отношение линейного давления к длине кривой контакта валка. Поэтому для определения остаточной влажности кожи нужна также зависимость длины контактной линии валка (ширины площадки контакта валка) от основных параметров валкового отжима кожи.
В связи с этим проведем исследование по изучению и разработке экспериментальной модели удельного давления.

Рисунок 1. Вид экспериментальной установки.
Конструкция экспериментальной установки (рисунок 1) позволяет осуществлять замену валка, а также изменять скорости валков и усилия их прижима. Предусмотрены комплекты валков с радиусами 0,050, 0,105 и 0,160 м (после намотки сукна радиусы их соответственно равнялись 0,058, 0,114 и 0,170 м), необходимые усилия прижима осуществлялись пружинно-винтовой системой, скорости валков регулировались реостатом, длина валков составляла 0,12 м.
Исследованию подвергались кожевенные полуфабрикаты крупного рогатого скота после хромового дубления (кожи). Для измерения ширины площадки контакта подготовлена тонкая и узкая лента, пропитанная цветным жидким агентом. Лента прикреплена к лицевой стороне образца кожи. При пропуске образца с лентой через жало валков, лента сжимается и упругое покрытие (сукно) верхнего валка поглощает отделяющихся от нее цветную жидкость. При отделении ленты от верхнего валка на сукне образуются цветной отпечаток (след), путем измерения которой определяется ширина площадки контакта.
Путем исследований области зоны контакта модулей [4, 11] и с учетом опыта эксплуатации валкового отжима кожи установлено, что основными факторами, влияющими на удельное давление, являются: интенсивность нагрузки Q ; радиус валка R ; скорость валка V .
Рабочая матрица составлена по матрице планов К. Кано для трехфакторного эксперимента. После реализации рабочей матрицы получены значения ширины площадки контакта L (таблица 1).
Таблица 1. Значения ширины площадки контакта L.
|
Рабочая матрица |
Ширина площадки контакта, мм |
||
|
Q |
R |
V |
L 0 |
|
40 |
0,114 |
0,22 |
0,0502 |
|
65 |
0,170 |
0,34 |
0,0676 |
|
65 |
0,058 |
0,34 |
0,0326 |
|
15 |
0,058 |
0,34 |
0,0179 |
|
15 |
0,170 |
0,34 |
0,0431 |
|
65 |
0,170 |
0,10 |
0,0665 |
|
65 |
0,058 |
0,10 |
0,0321 |
|
15 |
0,058 |
0,10 |
0,0234 |
|
15 |
0,170 |
0,10 |
0,0574 |
|
65 |
0,114 |
0,34 |
0,0539 |
|
40 |
0,058 |
0,34 |
0,0295 |
|
15 |
0,114 |
0,34 |
0,0355 |
|
65 |
0,058 |
0,22 |
0,0307 |
Современные инновации, системы и технологии // Modern Innovations, Systems and Technologies 2022; 2(4)
|
15 |
0,058 |
0,22 |
0,0222 |
|
15 |
0,170 |
0,22 |
0,0549 |
|
65 |
0,170 |
0,22 |
0,0637 |
|
40 |
0,170 |
0,34 |
0,0600 |
|
65 |
0,114 |
0,10 |
0,0530 |
|
40 |
0,058 |
0,10 |
0,0314 |
|
15 |
0,114 |
0,10 |
0,0467 |
|
40 |
0,170 |
0,10 |
0,0639 |
Для аппроксимации будем использовать методику, изложенную в работе [12],
согласно которой будем принимать степенную зависимость вида L о = CQ / R — ,
где
Qi =—, R = R-,
1Q 1R1
sr srsr
здесь Q sr = 40 кН/м , Rsr = 0,114 м, Vsr = 0,22 м/с.
Логарифмирование (1) дает ln Lo = ln C + a ln Q, + в ln R + у ln Vx.
Обозначив ln Lo = Y , ln C = n , ln Qx = Xx ,
In Rx = X2 и ln V = X 3, приведем
выражение (2) к линейному виду
Y = OXX + PX2 + yX^ + n.
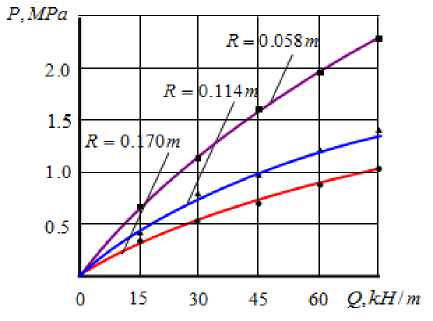
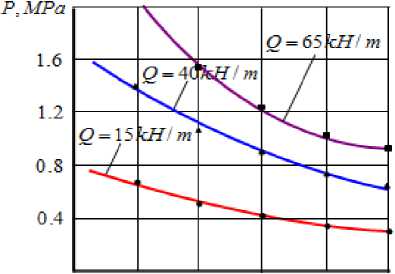
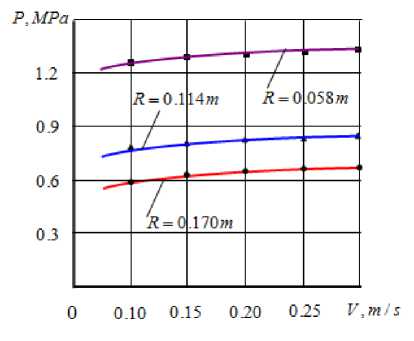
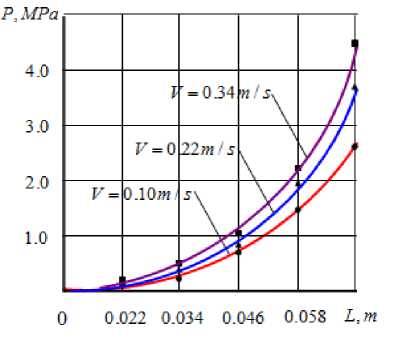
Параметры а, р, у и n находим методом наименьших квадратов, согласно которой, сумма квадратов отклонений £; экспериментальных точек от прямой должна быть наименьшей: F(a,P,y,n) = Е=-2 =E i=1 Таким образом, необходимо решить стандартную функции четырех переменных. Тогда имеем задачу – найти минимум + yX 1, X 3,+ nX 1,- X XiY^ =0. = E2(Y-(aX„ + PX „ + yX,,+ n))(-X1,) = 2Х (aX = + PX „X 2, да ,=1 Откуда имеем аХ X 2 + PZ X «X 2- + yZ X1X з. + ПЕ X к = Е XY i=1 i=1 =1 =1 =1 дF дF Определив аналогично, , др ду дF _ . и , получаем систему уравнений дn 21 21 21 2121 aEX 2 + вЕ X „X 2,+ yE X1X 3 , + nE X « =E X1 iY, i =1 i=1 i =1 i=1 21 21 21 2121 aE X1 -X 2 i + вЕ X 2 + YE X 2-X 3 i + nE X2 , = E X 2iY, i =1 i =1 i =1 i =1 21 21 21 2121 aE X «X з i + eE X „X з,. + YE X 3, + nE Xз- = E X =Y i=1 i =1 i=1 i=1 21 21 2121 aE X 1, + eE X 2,+ yE Xз, + 21П = E Y. i=1 i=1 i=1 После подстановки всех сумм, имеем 9,582a + 0,410 в + 0,526y - 3,963n = 14,549, 0,410a + 4,925в + 0,293y - 2,207n = 10,489, 0,526a + 0,293p + 6,507y - 2,832n = 8,446, -3,963a - 2,207в - 2,832y + 21n = -66,794. Система (6) имеет решение: a = 0,221, в = 0,740 , / = -0,09, n = -3,074. Отсюда, имеем C = en = e~3,074= 0,046. В процессы экспериментального исследования получили Locс = 0,0457. Это суммарная ширина площадки контакта. С учетом этого из выражения (1) можно получить следующие зависимости L = Q 0^1 R 074^ -°.09 (7) или с учетом выражений (2) L = 0.089Q0.221R 0'74V -0.09. (8) Оценим теперь точность аппроксимации опытных данных полученной формулой [13]: n V ^2 tT- = @Z = 0.044, v = ^ = 0.044 = 0.01. n - 2 V 19 nV21 Как видно, точность аппроксимации опытных данных формулой (7) более чем удовлетворительна. Известно [12], что P = Q,(9) где P - удельное давление. Тогда с учетом выражения (8), получим P = 11.23Q0.779R "0'74V0.09,(10) P = 56603.32L3^2 R -3.35V 0.41. (11) На рисунках 2-5 приведены графические интерпретации формулы (10) и (11). В работе [2] были определены аналитические зависимости, описывающие остаточную влажность кожи от факторов двухвалкового модуля: W = 92,580 -0,077^ 0,046 0,074 Рисунок 2. Зависимость удельного давления от линейного давления. 0 0.058 0.086 0.114 0.142 R,m Рисунок 3. Зависимость удельного давления от радиуса валка. Рисунок 4. Зависимость удельного давления от скорости валков. Рисунок 5. Зависимость удельного Давления от ширины площадки контакта. Из равенства (12) при значениях D = 0,22 м и v = 0,19 м/с, имеем W = 119,05 P-0,1. Из рисунка 6 следует, что с ростом удельного давления остаточная влажность кожи уменьшается и асимптотически приближается к определенной величине (например, при значениях R = 0,22 м v = 0,18 м/с к величине W = 57% ). Рисунок 6. Зависимость остаточной влажности кожи от удельного давления. РЕЗУЛЬТАТЫ 1. Получена эмпирическая зависимость, описывающая удельное давление как степенную функцию интенсивности нагрузки, диаметра и скорости валка. 2. Найдена аналитическая зависимость остаточной влажности кожи от удельного давления. ВЫВОДЫ Экспериментальным исследованием установлено, что • с увеличением интенсивности нагрузки ширина площадки контакта увеличивается и приближается к некоторой величине; • при больших значениях интенсивности нагрузки и диаметров валков, зависимость ширины площадки контакта от скорости валков характеризуется линейной функцией; • при меньших интенсивностях нагрузки с увеличением скорости валков ширина площадки контакта уменьшается, а при больших, наоборот, увеличивается; • с увеличением интенсивности нагрузки, скорости валка и ширины площадки контакта удельное давление увеличивается; • увеличение радиуса валка приводит к уменьшению удельного давления; • остаточная влажность кожи уменьшается и асимптотически приближается к определенной величине.