Исследование влияния геометрических параметров направляющего аппарата на энергетическую эффективность пневматического затвора тепломассообменных реакторов

Многие технологические процессы на промышленных предприятиях металлургической, химической, нефтяной, газовой и смежных отраслях сопровождаются выхлопами агрессивных газов, ухудшающих экологическую обстановку окружающей среды [1‒5]. Общеизвестные промышленные технологии получения современных материалов включают химические реакции под давлением при высоких температурах, сопровождающиеся фазовыми переходами [6‒15]. Такие процессы протекают в тепломассообменных аппаратах – реакторах – в составе барботажных колонн, аппаратов гетерогенного катализа и химического синтеза, фьюминг-печей, конвертеров, печей для выплавки стали погружным факелом и др. [1‒3, 6, 7, 9].

Рассматриваемые технологические процессы сопровождаются загрузкой сыпучего материала во внутреннюю полость реактора, находящуюся под избыточным давлением, через специальный канал загрузки, снабженный, как правило, механическим затвором. При загрузке запорное механическое устройство открыто, а при протекании химических реакций – закрыто. Применение механического запорного устройства сопряжено с нежелательными выбросами газов из полости реактора в процессе загрузки сырья, а также через зазоры затвора в его закрытом состоянии [2, 3, 8].

В качестве альтернативы механическому запорному устройству предлагается установка пневматического запорного устройства [15]. Данный высоконадежный аппарат не содержит подвижных частей. Абсолютное предотвращение выхлопа агрессивных газов осуществляется противотоком газа или смеси газов в загрузочном канале под давлением, равным или превышающим давления в реакторе. Рабочий процесс устройства сопровождается истечением активного потока газа и его закруткой, а также эжектированием агрессивного газа. При этом энергии активного потока газа дос- таточно для эжектирования твердых частиц загружаемого материала, что облегает загрузку в полость под избыточным давлением.

В работе [15] приводится метод расчета пневматического запорного устройства вихревого типа. Согласно работе [15], предложенный метод расчета позволяет решить как задачу определения оптимальных режимных параметров устройства при заданной геометрии, так и обратную задачу – определения оптимальных геометрических параметров при заданных режимных. Однако исследований, посвященных верификации и апробации научных основ данного метода, в научно-технической литературе обнаружить не удалось.

Постановка цели и задач

Целью данной работы является оценка влияния геометрических параметров направляющего аппарата на энергетическую эффективность пневматического затвора вихревого типа, а также применимости существующей физико-математической модели рабочего процесса затвора и основанного на ней метода расчета аппарата для проектирования оптимальной с точки зрения энергоэффективности конструкции затвора.

Для этого необходимо: проанализировать математическую модель рабочего процесса пневматического затвора и установить зависимость максимального запираемого давления в реакторе при заданных параметрах активного газа от количества лопаток, их толщины и угла установки; провести численное моделирование рабочего процесса затвора и сопоставить полученные результаты с расчетными.

Научная новизна

В результате исследования установлено, что угол установки, толщина и число лопаток направляющего аппарата существенно влияют на требуемые для запирания давления в реакторе пара- метры активного газа и, как следствие, энергетическую эффективность затвора.

Показано, что зависимость максимального запираемого давления от угла установки лопатки не является монотонно возрастающей и при достижении некоторой величины дальнейшее уменьшение угла установки приводит к снижению запираемого давления.

Теоретическая часть

Принципиальная схема пневматического затвора вихревого типа показана на рис. 1 [15].

По каналу загрузки сырья материал поступает в реактор. В процессе загрузки газ под давлением из компрессорной станции подается к каналу подвода активного воздуха. На выходе из канала подвода активного воздуха неподвижные лопатки создают закрученную струю воздуха кольцевой формы. При этом вектор абсолютной скорости газового потока раскладывается на осевую и тангенциальную составляющие. Образующийся в результате выброса струи в реактор вихрь запирает канал загрузки сырья.

Пневмозатвор является работоспособным при условии полного запирания загрузочного канала при отсутствии истечения выхлопных газов. Рабо- тоспособность устройства зависит от параметров, влияющих на истечение активного потока и на количество выхлопных газов. При истечении активного потока из кольцевого соплового устройства с лопастями формируется поток, направленный вдоль оси загрузочного канала, и вихревые течения. Осевой поток увлекает за собой газы из канала загрузки за счёт сил трения, а вихри интенсифицируют отклонение течения выхлопных газов. В совокупности это даёт эффект запирания загрузочного канала от поступления выхлопных газов и способствует загрузке материала в полость реактора.

Вихрь формируется за счёт отклонения активного потока лопастями в количестве n толщиной δ, высотой H , установленными под углом α к плоскости среза сопла. В результате истечения активного потока из кольцевого сопла с лопастями на выходе из него поток имеет осевые u_{х 3} и тангенциальные u _φ3 составляющие скорости с общим массовым расходом m . Формирование потока происходит при воздействии давления на входе в сопло p ₁ и температуры среды T ₁, а также давления на выходе из сопла p р (давление в реакторе) и температуры газов в реакторе T р . Интенсификация активного потока происходит при увеличении

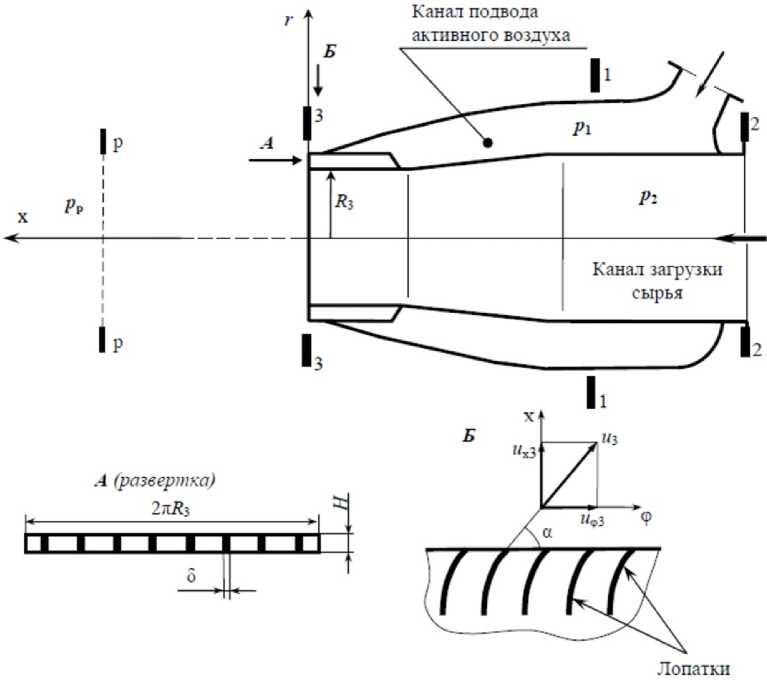
Рис. 1. Расчетная схема вихревого пневмозатвора: n – число лопаток;

δ – толщина лопатки; R ₃ – радиус запираемого отверстия; H – высота лопатки Fig. 1. Schematic diagram of a vortex-type pneumatic gate valve: n – number of blades;

δ – blade thickness; R ₃ – radius of the sealed hole; H – blade height

массового расхода активного газа m , тангенциальной составляющей скорости u φ3 , давления питания p 1 , температуры T 1 . Вышеперечисленные параметры связаны между собой уравнениями математической модели, на основе которой разработан метод расчета пневматического затвора, приведенный в работе [15]:

u ф3 =

² ( P p ^- P 2 ) p p + p 2 ;

R p T p   R 2 T 2

^ux 3 =

( R ₃ + H ) ²    (    -    ) - ^p 2 u 223

p ₃ H (2 R ₃ + H ) ( p ^p " p 2 )” 2 p ₃

n ( R + H )² ^ In ^ - nR ₃² '' ' u

³           2     2 P P p      ³    4

p ₃ n H (2 R ₃ + H )

m = u x ₃ p ₃ A ₃ = u x ₃ p ₃ H (2 R ₃ + H ) y ;

u

tg a= x ³ ;

^u ф 3

tg 2 a=P 2l1+l) i

2 P 3 (2 + Y )

„ (       „ . .2 A 2

^P p 1 1 ^P p ^u ф 3         Y

-p- 1 + ln^-^- +—i--- p 2 (       2 ^е P p J 2(1 + Y ) 2

где ρ₂, ρ₃, ρ_р – плотность газа в окружающей среде, на срезе кольцевого сопла и в реакторе соответственно; p ₂ – давление окружающей среды;

A 3 = n H (2 R ₃ + H ) - n 5 H = n H (2 R ₃ + H )v - эффективная площадь среза сопла;

• R 3 ‒ радиус канала загрузки;

• β    – коэффициент расхождения давления на срезе сопла и давления в реакторе;

п(2 R + H ) - n 5 ,      n 5

• w    =---- ³-------- = 1---коэффициент стеснения лопатками;

п(2 R ₃ + H )      п(2 R ₃ + H )

R

Y = — - относительный радиус канала загрузки.

Количество выхлопных газов в загрузочном канале зависит от давления запираемого потока выхлопных газов из реактора в загрузочный канал p р , температуры T р и радиуса загрузочного канала R 3 . Увеличение этих параметров увеличивает количество выхлопных газов в загрузочном канале.

Анализ уравнений (1)–(5) показывает, что максимальное запираемое давление в реакторе определяется величиной тангенциальной составляющей скорости активного газа на срезе кольцевого сопла: при ее увеличении максимальное запираемое давление растет. Данная зависимость, рассчитанная при абсолютном давлении в загрузочном канале p ₂ = 100 кПа, абсолютном давлении на входе в сопло p ₁ = 375 кПа, абсолютных температурах в загрузочном канале и на входе в сопло T ₁ = T ₂ = 293 К, абсолютной температуре в реакторе T _р = 673 К, радиусе канала загрузки R ₂ = 146 мм показана на рис. 2. Следует отметить, что монотонно возрастающая зависимость p р от u φ3 не является ожидаемой с точки зрения функционального назначения, создаваемого тангенциальной составляющей скорости вихря, при увеличении диаметра которого возможна газодинамическая картина потоков, не способствующая запиранию канала, – вихри локализуются на удаленной от канала загрузки периферии.

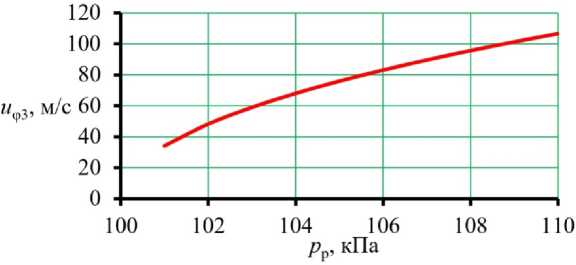
Рис. 2. Взаимосвязь величины тангенциальной составляющей скорости активного газа и максимального запираемого противодавления в реакторе Fig. 2. Relationship between the tangential component of the active gas velocity and the maximum sealed back pressure in the reactor

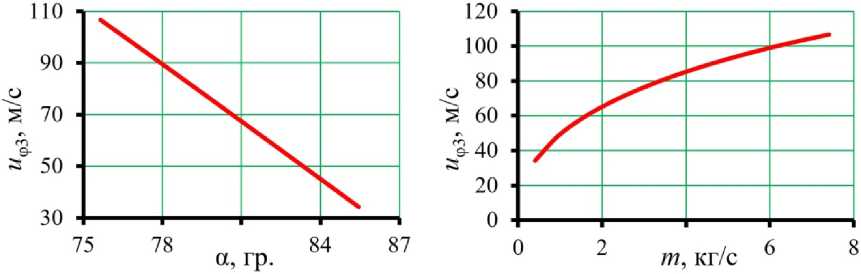
а)                                                             b)

Рис. 3. Влияние режимных и геометрических параметров затвора на величину тангенциальной составляющей скорости активного газа: а – угла установки лопатки направляющего аппарата; b – массового расхода активного газа

Fig. 3. The influence of the operating and geometric parameters of the valve on the value of the tangential component of the active gas velocity: a – of the installation angle of the guide vane; b – of mass flow rate of active gas

Согласно уравнениям (1)–(5), при заданной геометрии загрузочного канала, давлении и плотности активного газа, окружающей среды и газа в реакторе величина тангенциальной составляющей скорости активного газа u φ3 зависит от массового расхода активного газа m , угла установки лопатки направляющего аппарата α и коэффициента стеснения лопаток ψ, то есть толщины δ и количества n лопаток направляющего аппарата.

Зависимости тангенциальной составляющей скорости активного газа u _φ3 от угла установки лопатки α и массового расхода активного газа m показаны на рис. 3. Данные зависимости рассчитаны при тех же параметрах, которые описаны к рис. 2.

По кривой на рис. 3а видно, что с уменьшением угла установки лопатки α величина тангенциальной составляющей скорости газа u φ3 возрастает линейно. При этом кривая на рис. 3b показывает, что скорость u φ3 нарастает нелинейно при увеличении массового расхода m .

Оценить аналитически влияние толщины δ и количества n лопаток направляющего аппарата на тангенциальную составляющую скорости активного газа и таким образом на максимальную величину запираемого давления затруднительно вследствие того, что эти параметры в системе уравнений (1)–(5) не представлены в явном виде, однако определяют величину коэффициента стеснения лопаток ψ. Поэтому для исследования влияния параметров δ и n , а также для уточнения влияния угла установки и, следовательно, величины тангенциальной составляющей скорости газа на рабочий процесс устройства были проведены численные исследования с помощью трёхмерного моделирования физических процессов в затворе в программном пакете AnsysFluent .

Практическая часть

В качестве исходных данных для численного моделирования приняты следующие геометриче- ские размеры вихревого пневмозатвора, обозначение которых приведено на рис. 1:

• -    ширина сопла Н = 0,88 мм;

• -    радиус канала загрузки сырья R 2 = 150 мм;

• -    угол установки лопасти а = 80° (случаи а = { 40°; 60°; 80° } рассмотрены для конструкции с 8 лопатками и толщиной лопаток 2 мм);

• -    количество лопаток 8, 12 и 16;

• -    толщина лопатки 5 = 2 мм (случаи 5 = { 1 мм, 2 мм, 3 мм } рассмотрены для конструкции с 8 лопатками и углом установки лопасти α = 80°).

Также приняты следующие физические условия работы вихревого пневмозатвора:

• -    абсолютное давление воздуха перед соплом р ₁ = 400 кПа;

• -    абсолютное давление в реакторе p p = 100 кПа и 102 кПа;

• -    барометрическое давление в цехе p 2 = 100 кПа;

• -    температуры T 1 = T ₂ = 293 К, Т р = 673 К.

• -    массовый расход активного газа m = 0,577 кг/с.

При проведении моделирования вводились следующие допущения и упрощения:

• -    моделирование проводилось в стационарной постановке (установившееся течение);

• -    стенки конструкции являются гладкими, не-разрушаемыми и непроницаемыми;

• -    в качестве рабочего газа и вредных продуктов химических реакций в реакторе используется воздух.

В качестве математической модели, описывающей движение вязкого турбулентного газа, принимается система уравнений Навье – Стокса, осредненная по Рейнольдсу (RANS) [16‒19], замкнутая полуэмпирической моделью турбулентности Realizable k-ε [20‒24].

Семейства двухпараметрических диссипативных k-ε моделей турбулентности хорошо описывают свойства свободных сдвиговых течений моделью турбулентности. Realizabl k-ε модель по сравнению со стандартной k-ε моделью имеет два существенно важных отличия [24]:

• -    Realizable k-ε модель содержит альтернативную формулировку для турбулентной вязкости;

• -    модифицированное уравнение переноса для скорости диссипации ε было получено из точного уравнения для переноса среднеквадратичных колебаний завихренности.

Данная модель удовлетворяет точным математическим ограничениям по напряжениям Рейнольдса, вытекающим из физики турбулентной жидкости.

Ограничением является то, что можно получить нефизичные турбулентные вязкости в ситуациях, когда вычислительная область содержит как зоны с турбулентностью, так и зоны со стационарной жидкостью.

Твердотельная геометрическая модель конструкции с основными геометрическими размерами показана на рис. 4.

Расчетная схема модели вихревого пневмозатвора для CFD-анализа приведена на рис. 5.

Сформированная, на основе геометрической модели (рис. 5а), расчетная сеточная модель (рис. 5b)

состоит из тетраэдрических элементов (размер элемента 10 мм на поверхности каналов, 1 мм на поверхности каналов в области лопаток, 30 мм на поверхности реактора, 0,5 мм на поверхностях лопаток) и призматических элементов вблизи стенок (высота первого слоя – 0,5–0,02 мм в зависимости от зазора вблизи поверхности стенок, количество слоев – 2–6). Общее количество элементов составляет 13,97 млн.

Сеточная модель имеет следующие критерии качества расчетных элементов:

• -    минимальное значение коэффициента ортогональности 3∙10^–05;

• -    минимальное значение коэффициента пропорциональности 1390;

• -    минимальный объем расчетного элемента 1,71∙10^–13 м³, максимальный объем расчетного элемента 2,83∙10^–6 м³.

На рис. 6 показаны распределения параметров потока в продольном сечении при противодавлении в реакторе p _р = 0 кПа и 2 кПа (по избыточной шкале) для конструкции с 12 лопатками толщиной 2 мм.

На рис. 6b по векторному полю скоростей видно, что при противодавлении в реакторе 2 кПа

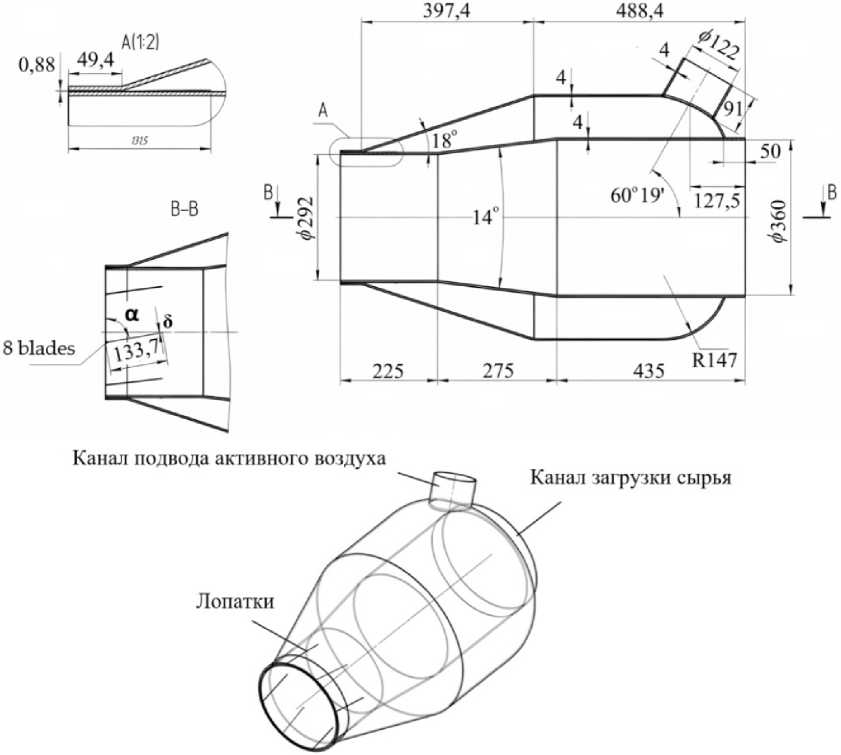
Рис. 4. Твердотельная геометрическая модель конструкции с основными геометрическими размерами

Fig. 4. Solid geometric model of the structure with basic geometric dimensions

поток активного газа выходит через сечение канала загрузки сырья. Это свидетельствует о срыве рабочего режима устройства – запирание полости реактора при противодавлении 2 кПа не происходит.

Результаты трёхмерного моделирования при различных количествах лопастей n , их толщин δ и углов установки α сведены в таблице.

Отрицательные величины массового расхода газа в таблице свидетельствуют о выбросе газа из полости реактора в окружающую среду при соответствующей величине противодавления в реакторе. Несмотря на то, что данная ситуация является недопустимой и затвор при рассматриваемом противодавлении не осуществляет полного запирания полости реактора, величина массового расхода выхлопа показывает запирающую способность устройства – чем больше массовый расход выхлопа, тем хуже запирающая способность затвора.

По результатам моделирования, приведенным в таблице, видно, что при одном и том же числе лопаток и их толщине уменьшение угла установки лопатки приводит к росту потребного давления активного воздуха и снижению максимальной величины запираемого давления в реакторе, что противоречит расчетам. Данное противоречие связано, как упоминалось ранее, с тем, что в математическом описании газодинамических процессов в затворе, на основе которого разработан метод расчета [15], не принимается во внимание функциональное назначение тангенциального компонента скорости активного газа и, как следствие, необходимой для запирания локализации вихревой области вблизи канала загрузки. Кроме того, увеличение толщины лопатки при неизменных угле установки и количестве лопаток ведет к снижению запирающей способности устройства. Такое же влияние оказывает и увеличение числа лопаток при неизменных угле установки и толщине лопаток. Однако следует ожидать, что зависимости максимального запираемого противодавления в реакторе от угла установки, числа и толщины лопаток имеют экстремум, по достижении которого дальнейшее увеличение угла установки и уменьшение количества и толщины лопаток приведет к снижению запирающей способности устройства.

Практическая значимость

Практическая значимость полученных результатов заключается в установленных ограничениях применимости существующего метода расчета пневматических затворов вихревого типа. Показано, что расчет оптимальных геометрических параметров направляющего аппарата, соответствующих наименьшим энергетическим затратам для запирания полости реактора, по существующему методу не дает корректных результатов и, следовательно, не может быть применим для профилирования проточной части при проектировании затворов вихревого типа.

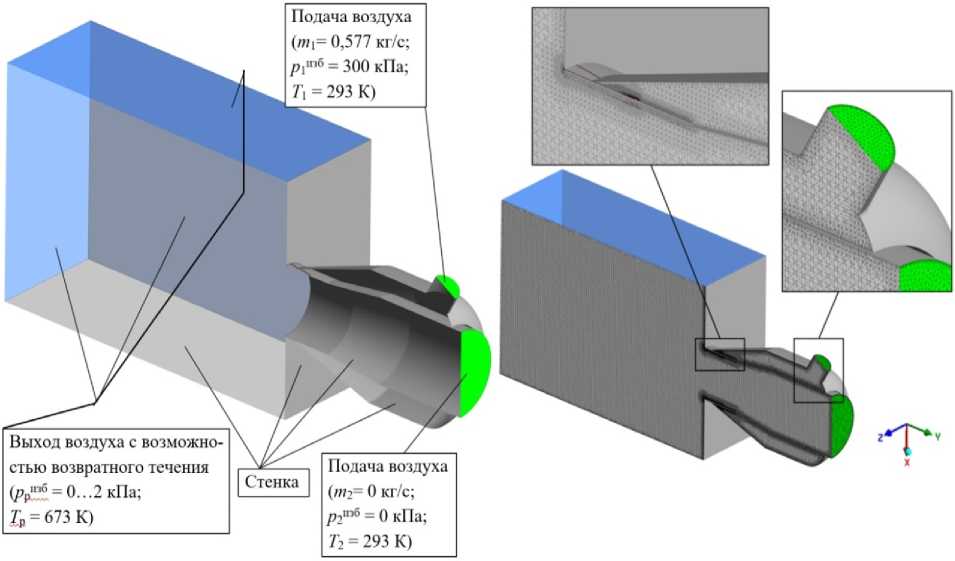
Рис. 5. К CFD-анализу параметров затвора: а – расчетная схема конструкции; b – конечно-элементная расчётная модель

Fig. 5. To CFD analysis of valve parameters: a – calculating diagram of the structure; b – finite element calculation model

Хабарова Д.Ф., Исмагилов А.Р., Исмагилов Д.Р.

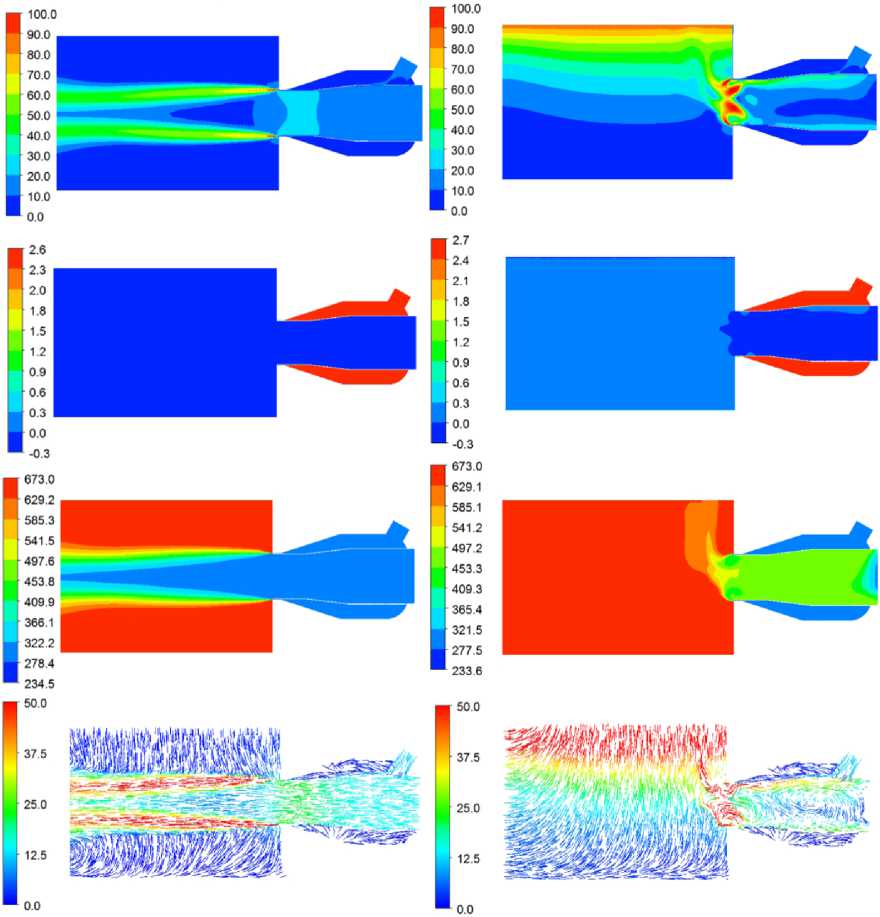
Рис. 6. Распределение параметров потока в продольном сечении (сверху вниз) результирующей скорости (локальный диапазон изменения, м/с), избыточного давления (ати), температуры (К), векторное поле скоростей (м/с): а – при противодавлении в реакторе 0 кПа; b – при противодавлении в реакторе 2 кПа Fig. 6. Distribution of flow parameters in the longitudinal section (from top to bottom) resulting velocity (local range of change, m/s), excess pressure (atm), temperature (K), vector velocity field (m/s): a – at a back pressure in the reactor of 0 kPa; b – at a back pressure in the reactor of 2 kPa

Результаты моделирования Simulation results

Количество лопаток n	Толщина лопаток δ, мм	Угол установки лопаток α, град.	Избыточное давление на входе в канал подвода активного газа, кПа		Массовый расход газа через канал загрузки (выхлоп), кг/с
			Противодавление в реакторе (давление сопротивления на границах области реактора, кроме верхней поверхности), кПа
			0	2	0	2
8	2	40	–	530,3	–	–1,019
8	2	60	–	328,3	–	–0,863
8	1	80	259	270,3	1,49	–0,692
	2		262,8	273,3	1,50	–0,698
	3		255,6	267,3	1,52	–0,752
12	2	80	261,7	271,3	1,66	–0,771
16	2	80	267,8	280,5	1,68	–0,811

Заключение

Проведено исследование влияния геометрии направляющего аппарата на запирающую способность пневматического затвора вихревого типа. Исследование показало, что существующий метод расчета затвора вихревого типа не учитывает, что запирание полости реактора происходит только при локализации вихрей в пределах некоторых границ вблизи канала загрузки и, следовательно, расчетные зависимости метода неприменимы для определения оптимального сочетания величин угла установки, толщины и количества лопаток.

Численным моделированием газодинамических процессов в пневматическом затворе вихревого типа показано, что уменьшение угла установ- ки лопаток, а также увеличение толщины и числа лопаток в рассмотренном диапазоне параметров оказывают негативное влияние на запирающую способность затвора. Однако следует ожидать, что зависимость максимального запираемого давления в полости реактора при некоторых заданных параметрах активного газа от величин угла установки, толщины и количества лопаток имеют экстремум. Исследование этих зависимостей на экстремум требует проведения расчета в широком диапазоне параметров и позволит разработать метод определения оптимального сочетания геометрических параметров направляющего аппарата, обеспечивающего наиболее энергоэффективный режим работы затвора.