Исследование влияния импульсных стабилизаторов напряжения на адмитанс и устойчивость имитаторов солнечных батарей с каскадным включением усилителей мощности

Автор: Мизрах Енис Аврумович, Сидоров Александр Сергеевич, Ткачев Степан Борисович

Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau

Рубрика: Технологические процессы и материалы

Статья в выпуске: 4 (37), 2011 года.

Бесплатный доступ

Исследовано влияние динамических свойств импульсных стабилизаторов напряжения на адмитанс и устойчивость имитаторов солнечных батарей с каскадным включением непрерывного и импульсного усилителей мощности. Сформулированы ограничения на параметры сглаживающего LC-фильтра импульсного стабилизатора напряжения.

Импульсный стабилизатор напряжения, имитатор солнечной батареи, устойчивость, адмитанс

Короткий адрес: https://sciup.org/148176646

IDR: 148176646

Текст научной статьи Исследование влияния импульсных стабилизаторов напряжения на адмитанс и устойчивость имитаторов солнечных батарей с каскадным включением усилителей мощности

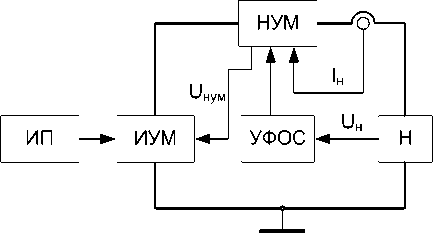
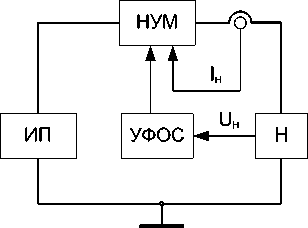
В настоящее время одной из перспективных топологий имитаторов солнечных батарей (ИСБ) (рис. 1), позволяющей с требуемой точностью воспроизводить ВАХ и импеданс (адмитанс) солнечных батарей мощностью более 1 кВт, является топология ИСБ с каскадным включением непрерывного и импульсного усилителей мощности (рис. 1, а ), где ограничение мощности рассеивания непрерывного усилителя мощности (НУМ) осуществляется путем стабилизации напряжения на его регулирующих элементах (РЭ) с помощью импульсного усилителя мощности (ИУМ). Данная топология строится на основе другой топологии – ИСБ последовательного типа (рис. 1, б ).

Вопросы устойчивой работы ИСБ последовательного типа и влияния импеданса источника питания на адмитанс имитатора достаточно хорошо проработаны в [1; 2]. Но, в ИСБ с каскадным включением НУМ и ИУМ в отличие от ИСБ последовательного типа появляется еще одна отрицательная связь по напряжению, причем ИУМ стабилизирует только часть своего выходного напряжения, а другая часть определяется нагрузкой. Актуальными являются вопросы влияния динамических свойств импульсного стабилизатора напряжения на устойчивость и адмитанс ИСБ с каскадным включением НУМ и ИУМ.

а б

Рис. 1. Топологии имитаторов солнечных батарей:

а – ИСБ с каскадным включением НУМ и ИУМ; б – ИСБ последовательного типа; ИП – источник питания;

ИУМ – импульсный усилитель мощности; Н – нагрузка; НУМ – непрерывный усилитель мощности;

УФОС – устройство функциональной обратной связи

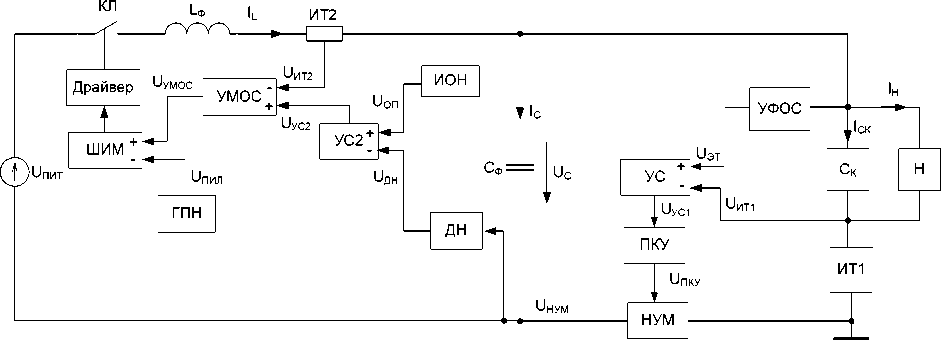
Рис. 2. Структурная схема ИСБ с каскадным включением НУМ и ИУМ

Структурная схема ИСБ с каскадным включением НУМ и ИУМ представлена на рис. 2. В структуре данного имитатора можно выделить три большие подсистемы:

1. Непрерывный стабилизатор тока (НСТ) нагрузки, образованный усилителем-сумматором (УС), последовательным корректирующим устройством (ПКУ), НУМ, измерителем тока (ИТ) и корректирующим конденсатором (CК).
2. Устройство функциональной обратной связи (УФОС) по напряжению нагрузки, которое задает вольтамперную характеристику (ВАХ) солнечной батареи (СБ) в некотором масштабе и вырабатывает эталонное напряжение UЭТ для стабилизатора тока.
3. Импульсный стабилизатор напряжения (ИСН) на регулирующих элементах НУМ, которой состоит из делителя напряжения (ДН), источника опорного напряжения (ИОН), УС2, усилителя местной обратной связи (УМОС) по среднему току дросселя, генератора пилообразного напряжения (ГПН), широтноимпульсного модулятора (ШИМ), драйвера, ключа (КЛ), источника питания (UПИТ), сглаживающего фильтра (L ф и C ф ).

Функциональная схема для приращений ИСБ с каскадным включением НУМ и ИУМ, полученная путем объединения функциональных схем ИСБ последовательного типа [1] и функциональной схемы импульсного стабилизатора напряжения [3–5], представлена на рис. 3.

Согласно работе [6], передаточные функции устройств НСТ и их параметры имеют следующий вид:

– передаточная функция НУМ по управлению:

^ НУМ ⁽ ⁵ ) =

К НУМ

^Т НУМ ⁵ + 2 ^ НУМ ^Т НУМ ⁵ + ¹

где К _НУМ ® 2,45 А/В - коэффициент передачи НУМ по управлению; Т _НУМ ® 1,14^10^ 7 с - постоянная времени НУМ по управлению; ^ _Н ум ® 0,75 - коэффициент относительного демпфирования;

– адмитанс НУМ v , х ^ОНУМ (ТУНУМ15 + 1)

^ НУМ ( 5 ) =------ ТЪ -------------------,

Т у 22 5 ² + 2^унум Т унум₂ 5 + 1

Y _НУМ 2 Y НУМ Y НУМ 2

где Y _0НУМ ® 0,2^ 10 ³ Сим - активная составляющая адми-танса НУМ; Т у и _У М1 ® 3,25^10^ с, Т у и _У М2 ® 1,35'10 ⁷ с -постоянные времени адмитанса НУМ; ^ у Н _УМ ® 0,95 -относительный коэффициент демпфирования;

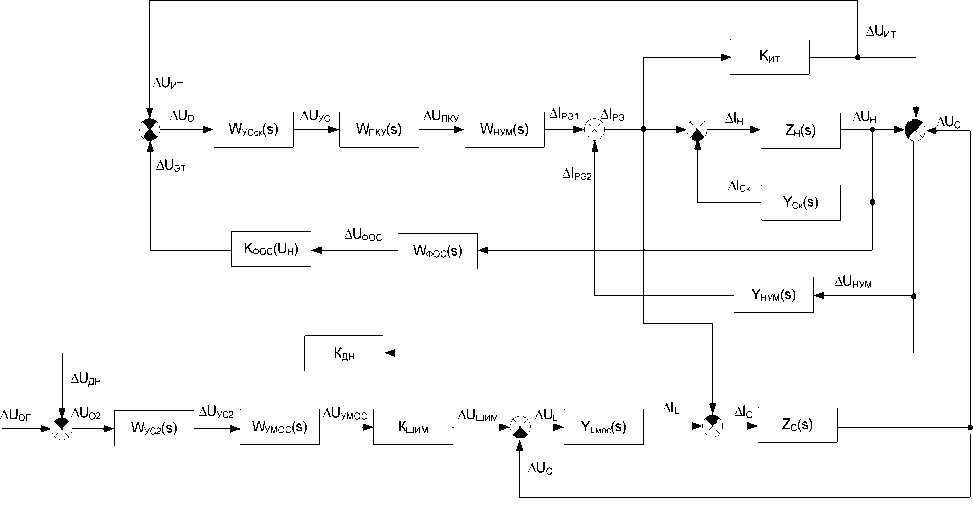
Рис. 3. Функциональная схема имитатора СБ с каскадным включением НУМ и ИУМ

- передаточная функция УС

W ус ( s ) =

К УС

T /С s + ¹

Согласно [3-5], передаточные функции устройств ИСН имеют следующий вид:

- передаточная функция УМОС:

где К _УС и Т _УС - коэффициент передачи и постоянная времени УС;

- передаточная функция ПКУ w ( (TПКУ1 s + MTEY2s + 1)

^W ПКУ ⁽ s ) = ,_1Ч’

⁽ ^T ПКУ3 s + ¹⁾⁽ ^T ПКУ4 s + ¹⁾

где Т _ПКУ i - постоянные времени ПКУ.

адмитанс корректирующего конденсатора:

Y C К ( s ) = C _К s , где C К - емкость корректирующего

W УМОС⁽ ^s ) =

К УМОС ⁽ T Z s + ¹⁾ s ( Т Р s + 1)

где К _УМОС - коэффициент усиления при ю = 1, T_Z и T P - постоянные времени, причем T_Z > T P ;

- коэффициент передачи ШИМ и КЛ равен К шИм = U _пиТ / U _ПИЛ, где U п _ИТ - напряжение источника питания ИСН; U _ПИЛ - размах пилообразного напря-

конденсатора.

Согласно [2] К _УС, Т _УС, Т _ПКУ i , C К рассчитываются исходя из воспроизведения имитатором требуемого адмитанса СБ.

Математическая модель УФОС в малосигнальном режиме представляет собой дифференциальный коэффициент передачи K _ФОС (U _Н , I _КЗ , U ХХ ) = = ^д ^ ФОС ⁽ ^U Н , I _КЗ , U _ХХ)/ дU _Н| , зависящий от точки линеаризации ПХ и параметров ВАХ ИСБ, и передаточную функцию, которая имеет вид

жения;

- адмитанс дросселя фильтра с учетом местной обратной связи (МОС) по среднему току дросселя:

Y ( s ) = Y L ⁽ s )

L ^МОс() 1 + W moc ( s ),

Wo (s) =

^Т ФОС1 s + ² ^ ФОС1 ^T ФОС1 ^s + ¹ ) ^х

где Y L ₁ ( s ) =----------------- - адмитанс дросселя

L ф s + ^Rl ф + R и _Т 2

фильтра с учетом активных потерь в преобразователе (потери в коммутирующих полупроводниковых элементах и статические потери в обмотках трансформатора и дросселя выходного фильтра) и в измерителе среднего тока дросселя; L _Ф - индуктивность дросселя фильтра; R L _Ф - сопротивление потерь; R _иТ2 - со-

ФОС2 s + ² ^ ФОС2 ^Т ФОС2

¹ ) ⁽ ^Т ФОС3 s + ¹ ⁾

где Т Фос1 = 8,84 - 10^-8 с, Т фос2 = 2,12 - 10^-8 с, Т Ф _ОС3 = 1,6 - 10 ⁸с - постоянные времени; ^ _ФОС1 = 0,5, ^ _ФОС2 = 0,1 - коэффициенты относительного демпфирования.

противление измерителя среднего тока дросселя, ^W MOC ⁽ ^s ) = W /МОС ⁽ ^s ) K ШИМ Y L ⁽ ^s ) K ИТ2 ^{- передаточная} функция разомкнутого контура МОС по среднему току дросселя;

- импеданс конденсатора фильтра Z_C ( s ) с учетом эквивалентного последовательного сопротивления (ESR):

Zc ( 5 ) =

R c Ф C Ф 5 + 1

C Ф s

где С _Ф - емкость конденсатора фильтра; R_c _Ф - экви

валентное последовательное сопротивление конден

^Ж РКИСН хх ⁽ ⁵ ) = ^Ж УС2⁽ ⁵ ⁾ ^Ж умос ⁽ ⁵ ) K ШИМ ^Х Y L МОС ⁽ ⁵ ) ^z фмос ⁽ ⁵ ) К ДН .

Выходной импеданс ИСН определяется щим выражением:

следую-

сатора.

При анализе влияния динамических свойств ИСН на динамические свойства ИСБ удобнее пользоваться следующими характеристиками ИСН: передаточной функцией разомкнутого контура ИСН и импедансами фильтра и ИСН.

В [4] показано, что между частотой преобразования f_m, частотой среза разомкнутого конутра МОС f СРмос * f ш/(2 л ), частотами f z = 1/(2 п T z ) и f p = 1/(2 п T р ) существует соотношение f_z < f_CР м _ос < f_ПР = f_P , которое с учетом условия |^ _МО с ( j ю )| » 1, где 0 < ю < ю срмос ,

Z ( 5 ) = ^Z ^ФМ0С ⁽ ⁵ )

1 + Ж 'р.. Н. ( 5 )

Проанализируем влияние динамических свойств ИСН на адмитанс имитатора. В таблице представлены адмитанс ИСБ с каскадным включением НУМ и ИУМ и, в целях сравнения, адмитанс ИСБ последовательного типа [2]. Сравнивая соответствующие слагаемые

позволяет упростить (1):

Y L MOC ⁽ j ^ю ⁾ *

_________________1_________________

^WУМОС ⁽ j ^ю ⁾ K ШИМ K ИТ2

j ю

К УМОС K ШИМ K ИТ2 ^(Tz^j ^{ю +} 1)

^ю< ^ю СР MOC .

Согласно (2) в диапазоне частот 0 < ю < 1/ T Z благодаря МОС адмитанс дросселя приобретает емкостной характер, где эквивалентная емкость дросселя

адмитансов имитаторов, можно сделать вывод, что охват РЭ НУМ обратной связью по напряжению приводит к изменению адмитанса НУМ.

Рассмотрим влияние передаточной функции разомкнутого контура ИСН в режиме ХХ на Y _НУМ( 5 ). Как правило, в ИСН между частотой среза разомкнутого контура ИСН и_СРисн, частотой среза разомкнутого контура М0С по среднему току дросселя и_СРмос и частотой преобразования и_пр выполняется соотношение и_СРисн< и_СРмос< и_пр [4]. Поэтому, с учетом выражение (2) в диапазоне частот 0 < ю < и_СРисн ПФ W ркисн хх принимает вид:

^Ж РКИСН хх ⁽ j ^ю ⁾ =

равна

C L

К УМОС K ШИМ K ИТ2

^Ж УС2 ⁽ j ^ю ⁾ ^Ж УМ0С ⁽ j ^ю ⁾ K ШИМ ^Z ФМОС ⁽ j ^ю ⁾ К дн = (5)

W yMOC ⁽ j ^ю ⁾ K ШИМ К ИТ2

Адмитанс фильтра с МОС определяется выражением:

Y OMOC ⁽ ⁵ ) = Y L МОС ⁽ ⁵ ) ⁺

1 z C ( 5 )

= Y L MOC ⁽ ⁵ ) ⁺ Y C ⁽ ⁵ ) .

Передаточная функция разомкнутого контура ИСН имеет вид:

W УС2⁽ ⁵ Ж уМОС ⁽ ⁵ ) K ШИМ ^Х

W ( \ - ^Х YL МОС ⁽ ⁵ ) ^z фмос ⁽ ⁵ ) К ДН

⁽ ⁵ ) = 1 + Z ФМОС ( 5 ) Y H ( 5 ) ’

где Z _ФМ0С( 5 ) = 1/ Y _фмОс( 5 ) - эквивалентный импеданс фильтра; Y _H(s) - адмитанс нагрузки.

В режиме ХХ , когда Y _Н( 5 ) = 0, передаточная функция разомкнутого контура ИСН принимает вид:

^Ж УС2 ⁽ j ^ю ⁾ ^Z ФМОС ⁽ j ^ю ⁾ К ДН = ---------------------------------- .

К ИТ2

Согласно (5) в диапазоне частот 0 < ю < и_СРисн существенное влияние на W _{РКИСНхх} оказывает импеданс фильтра Z _ФМ0С с MOC по среднему току дросселя, который в области низких и средних частот имеет емкостной характер, т. е. ПФ W РКИСНхх обладает относительно большим коэффициентом передачи в области низких и средних частот. Поэтому, благодаря охвату обратной связью по напряжению регулирующих элементов НУМ модуль адмитансно-частотной характеристики (АдЧХ) | Y _НУМ( /' ю )| в диапазоне частот 0 < ю < и_СРисн уменьшается по сравнению с модулем АдЧХ | Y _НУМ( /' ю )|, что согласно работе [2] положительно сказывается как на статической, так и на динамической точности имитатора.

Адмитансы имитторов

ИСБ с каскадным включением НУМ и ИУМ	ИСБ последовательного типа
Y KAC ⁽ ⁵ , U Н ) = Y CT ⁽ ⁵ ) ⁺ Y ОС ⁽ ⁵ , U Н ) ⁺ ^Y Cr ⁽ ⁵ )	^Y noc ⁽ ⁵ , U Н ) = Y DOC ⁽ ⁵ , U Н ) ⁺ ^ СТ ⁽ ⁵ ) ⁺ ^Y C_K ⁽ ⁵ )
Y Cr ( 5 ) =------------------------------------ 1 ⁺ W CK ⁽ ⁵ ) ⁺ K ИтЖуМ ⁽ ⁵ ) ⁺ ^Z ИСН ⁽ ⁵ ) ^Y HyM ⁽ ⁵ )	Y _CТ ( 5 ) =------------- ^ УМ^------------- ¹ ⁺ W CK ⁽ ⁵ ) ⁺ K ИТ Y HyM ⁽ ⁵ ) ⁺ ^Z ИП ⁽ ⁵ ⁾ ^Y HyM ⁽ ⁵ )
Yк ( ₅ U ) = K Ф0С ⁽ ^U Н ⁾ ^Ж фос ⁽ ⁵ ) W VC ⁽ ⁵ ) ^Ж пку ⁽ ⁵ ) ^Ж нум ⁽ ⁵ ) ^Ф0С ’ ^Н 1 + Ж ск ( 5 ) + K ИТ1 Y нУМ ( 5 ) + Z ИСН ( 5 Жум ( 5 )	Y ( ₅ U ) = K фос ⁽ ^U н ⁾ ^Ж фос ⁽ ⁵ ) W yc ⁽ ⁵ ) ^Ж пку ⁽ ⁵ ) ^Ж нум ⁽ ⁵ ) ¹ ⁺ W CK ⁽ ⁵ ) ⁺ K ИТ Y HyM ⁽ ⁵ ) ⁺ ^Z ИП ⁽ ⁵ ⁾ ^Y HyM ⁽ ⁵ )
V ___ Y HyM ⁽ ⁵ ) ___ ⁷ НУМ ⁽ ⁵ ) = ! ТТЛ z X 1 ⁺ ^Ж РКИСН хх ⁽ ⁵ )
W CK ( ⁵ ) = W УС ( ⁵ ⁾ ^Ж пку ( ⁵ ⁾ ^Ж нум ( ⁵ ) К ИТ

В работе [2] было получено условие, которому должен удовлетворять импеданс ИП ИСБ последовательного типа, исходя из наименьшего влияния на адмитанс имитатора

Проанализируем импеданс ИСН. С учетом (5) импеданс ИСН (4) в диапазоне частот 0 < ю < и_СРисн принимает вид:

Z исн ⁽ ^j ^ю ⁾ =

Z Фэкв ⁽ ^j ^ю ⁾ ^W УMОС ⁽ ^j ^ю ⁾ K ШИМ К ИТ 2 W yC2 ⁽ ^j ^ю Ж уМОС ⁽ ^j ^ю ⁾ K ШИМ Z Фэкв ⁽ ^j ^ю ⁾ К ДН

K ИТ 2 ~ K ИТ 2

W УС2⁽ s ) К ДН K УС2 К ДН

|Z И _П ( j ю )| < | z ИПпр ( j ю ) | = ¹ + W' ' ⁽ j ® ) — K ит

^{1 1 У} НУМ⁽ j ^ю ⁾

ю е 0... ю срж ,

где Z _ИПпр ( j ю ) - модуль предельной импедансно

частотной характеристики (ИЧХ) ИП ИСБ последова

тельного типа; ю _СРж - желаемая частота среза РК НСТ; W _РКж - желаемая передаточная функция РК НСТ, которая в диапазоне частот 0 < ю < и_СРж

т. е. имеет чисто активный характер. Выше частоты среза разомкнутого контура ИСН и_СРисн импеданс ИСН определяется импедансом (параметрами) LC -фильтра.

Учитывая, что обычно выполняются условия К _ИТ2< 1 Ом, К _УС2 » 1, К д _Н < 1, то в диапазоне частот 0 < ю < и_СРисн, где и_СРисн обычно не превышает несколько килогерц, условие (6) автоматически выполняется. Таким образом, (6) накладывает ограничения только на параметры LC -фильтра.

Определим наибольшее значение индуктивности дросселя фильтра L _Фмакс. Приравнивая L Фмакс ^ю = Z ИПпр⁽ ^j ^ю)| при ^ю = ^ю срж , получим

имеет вид

W ркж ( j ю ) =

К РКж

( Г ркж1 j ю + 1) ’

где К _РКж - желаемый коэффициент передачи, T РКж1 = К РКж / ^ю СРж .

Так как Z _ИП( s ) = Z _ИСН( s ), то модуль ИЧХ ИСН должен удовлетворять условию:

Z ИСН ⁽ ^j ^ю)| < Z ИПпр ⁽ ^j ^ю ⁾|

1 + W ркж ( j ю ) ^Y НУM ⁽ ^j ^ю ⁾

- K _ИТ

юе 0... ю _СРж .

График | Z _ИПпр ( j ю )| при типовых ю _СРж ~ 3,14 - 10⁶ с ¹и К _РКж = 200 представлен на рис. 4. Как видно из графика в области НЧ импеданс ИП может быть порядка мегаом, но по мере роста частоты он должен становиться меньше.

Z ИПпр ⁽ ^j ^ю СРж )| L Фмакс = .

ω СРж

При ю _СРж ~ 3,14 - 10⁶ с^-1 получим L _Фмакс ® 1,8мкГн. На рис. 4 представлен модуль ИЧХ ИСН при Z _ИСН0 = 0,050м и L _Ф = L _Фмакс. Как видно из графиков, условие (6) в диапазоне частот 0 < ю < и_СРж в полной мере выполняется.

Как показывает практика, полученная на примере величина индуктивности дросселя не достаточна для выполнения условия непрерывности тока дросселя, поэтому определим наименьшую емкость конденсатора, при которой индуктивность дросселя не будет оказывать влияния на адмитанс ИСБ. Для этого рассмотрим условие C Ф_МИН ю = 1/ | Z ИПпр ( j ю )| при ю = ю СРж:

Фмин

≤Z

ИПпр ⁽ ^j ^ю СРж )|

ω СРж

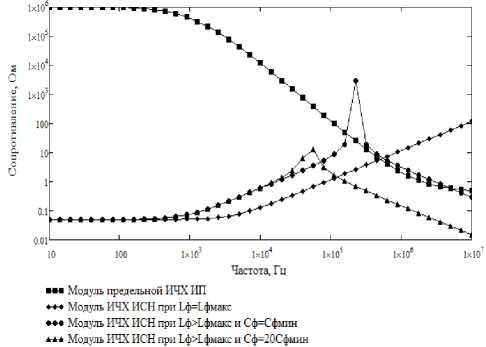
Рис. 4. Графики ИЧХ ИСН

При ю _СРж ~ 3,14 - 10⁶ с ¹ получим С _Фмин ® 53 нФ. Модуль ИЧХ ИСН при L ф > L Ф _мак с и С ф = С Фмин представлен на рис. 4. Как видно из графика, на частоте сопряжения индуктивной составляющей ИЧХ ИСН и импеданса конденсатора образуется резонансный выброс, который не позволяет в полной мере выполнить условие (6). Поэтому величину емкости конденсатора С _Ф предлагается выбирать с запасом в 20-100 раз:

C Ф 2 ²⁰ _r ——¹ . (8)

Z ИПпр ⁽ J ^ю СРж )| ω СРж

Модуль ИЧХ ИСН при L Ф > L Фмакс и С Ф = 20 С Фмин ~ ~ 1 мкФ представлен на рис. 4. Видно, что теперь условие (6) в диапазоне частот 0 < ю < и_СРж в полной мере выполняется.

Таким образом, при расчете параметров LC -фильтра ИСН для ИСБ с каскадным включением НУМ и ИУМ

накладывается ограничение, согласно которому емкость конденсатора фильтра должна быть не меньше некоторой минимальной величины.

Рассмотрим вопрос устойчивой работы ИСН. Особенностью работы ИСН в составе ИСБ с каскадным включением НУМ и ИУМ является то, что ИСН производит стабилизацию только части своего выходного напряжения - напряжение на РЭ НУМ, тогда как дру гая часть - напряжение нагрузки - зависит от импеданса нагрузки и формируется НСТ и УФОС. Поэтому для расчета КУ, обеспечивающего устойчивую работу ИСН, необходимо определить ПФ РК ИСН с учетом НСТ и УФОС.

Используя формулу Мезона, по функциональной схеме, представленной на рис. 3, получим передаточную функцию разомкнутого контура ИСН, работающего в составе ИСБ с каскадным включением НУМ и ИУМ:

A U _ДН ( 5 )

^ РКИСНк ⁽ ⁵ , U H ) =

A U O2 ( 5 )

= ^W РКИCН хх ⁽ ⁵ )

¹ + Z H ⁽ ⁵ ) ^У ПОС ⁽ ⁵ , U H )

** ,

¹ + Z H ⁽ ⁵ ) ^У ПОС ⁽ ⁵ , U H )

где

У ПоС ( 5 , U н ) = Сс ( 5 , U н ) + У ск ( 5 ), K ФОС ⁽ ^U Н ) ^ ФОС ⁽ ⁵ ⁾ ^W VCck ⁽ ⁵ ) ^Х

- * ^Х ^W ПКУ ⁽ ⁵ ⁾ ^W НУМ ⁽ ⁵ )

ФОС ⁽ ⁵ , ^U H ) = , z х

** ** **

^У ПОС ⁽ ⁵ , U H ) = ^У ФОС ⁽ ⁵ , U H ) ⁺ ^У Ст ⁽ ⁵ , U H ) ⁺ ^У Ск ⁽ ⁵ )

^У ФОС ⁽ ⁵ , U н ) =

K ФОС ⁽ ^U Н ) ^W ФОС ⁽ ⁵ ) ^W YCgk ⁽ ⁵ Ж пКУ ⁽ ⁵ ⁾ ^W НУМ ⁽ ⁵ ) 1 + W ck ( 5 ) + K ит1 У нум ( 5 ) + Z Фмос ( 5 У нум ( 5 ) ’

У ст ⁽ ⁵ , U н ) =

_________________ ^У нум ⁽ ⁵ ) _________________

1 + W ck ( 5 ) + K ИТ1 ^У НУМ ⁽ ⁵ ) ⁺ Z Фмос ⁽ ⁵ ) ^У нум ⁽ ⁵ )

Графики | ^У Пос ⁽ j to , U н)| ^и | ^У ПОс ⁽ j to U н)| при ^ти повых значениях С _Ф = 10 мкФ и L _Ф = 200 мкГн представлены на рис. 5.

Как видно из графиков, в диапазоне частот до нескольких килогерц, являющихся частотой среза РК ИСН, модули выражений |у П _ос ( j to , U _н)| и У пО _С ( j to , U _н ) совпадают, что позволяет упростить (9):

^W PKHCHk ⁽ ⁵ , U H ) ~ ^W PKHCH xv ⁽ ⁵ ) •

Таким образом, при исследовании устойчивости ИСН, работающего в составе ИСБ с каскадным включением НУМ и ИУМ, можно использовать передаточную функцию ИСН в режиме ХХ (3).

Условие устойчивости по частотным характеристикам | Wркиснхх(j'to)| и Фрк = arg( Wркиснхх(j'to)) имеет вид toCP < toП, где tocp - частота среза, при которой | Wркиснххj'tocp)| = 1; toП - частота, при которой фРК(юП) = -180°.

Как правило, для обеспечения устойчивой работы ИСН между частотой среза разомкнутого контура ИСН to _с p и частотой преобразования (модуляции) to _пpдолжно выполняться условие to _сp < to _пp/5 [4; 5]. В то же время, как показывают результаты моделирования [1], быстродействие ИСН оказывает существенное влияние на качество переходных процессов на токовой ветви ВАХ имитатора СБ. Поэтому, для повышения качества переходных процессов ИСБ с каскадным включением НУМ и ИУМ необходимо, чтобы частота среза ИСН была как можно больше. Руководствуясь наибольшим быстродействием ИСН, используя передаточную функцию разомкнутого контура ИСН в режиме ХХ (3) и методы, изложенные в [4; 5], можно провести синтез корректирующего устройства, обеспечивающего устойчивость и требуемого быстродействие ИСН.

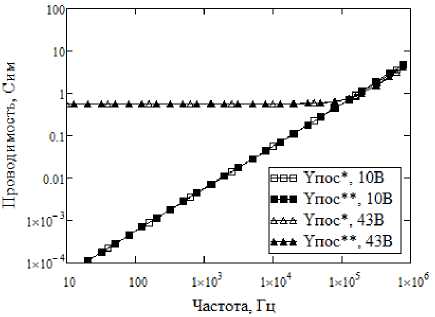
Рис. 5. Графики I ^У пос ⁽ j ^to , ^U н )| ^и | ^У пос ⁽ j ^to , ^U н )

Таким образом, в работе исследовано влияние импульсного стабилизатора напряжения на адмитанс и устойчивость имитатора с каскадным включением непрерывного и импульсного усилителей мощности. Показано, что для наименьшего влияния импеданса ИСН на адмитанс имитатора емкость конденсатора фильтра ИСН должна удовлетворять условию (8). Для исследования и обеспечения устойчивости ИСН следует использовать передаточную функцию разомкнутого контура ИСН в режиме холостого хода (3).

Статья научная