Исследование влияния ионосферы земли на фарадеевское вращение вектора поляризации радиоволн в высокочастотном диапазоне

Введение. Постановка задачи

Изучено влияние ионосферы Земли на распространение радиоволн различных диапазонов. В работах [1–3] подробно рассмотрено влияние ионосферы на радиоволны P- диапазона (430 МГц). В данной работе сопоставлено влияние ионосферной плазмы на параметры радиосигналов для трех различных частот: 200 МГц, 430 МГц и 1200 МГц. Актуальность работы связана с тем, что радиоволны с такими частотами применяются при проектировании космических антенн с синтезированной апертурой [4], а также используются для восстановления профиля электронной концентрации ионосферной плазмы методом радиотомографии [5].

В работе рассмотрена модель дневной (12 час) ионосферной плазмы относительно точки с координатами 40°с. ш., 30°в. д. Профиль электронной концентрации представлен на рис. 1 (см. [6]).

На таких высоких частотах предполагается, что траекторию луча можно считать прямой линией, соединяющей передатчик и приемник, и визуально это действительно так. Однако влияние ионосферы на отдельные параметры является весьма существенным.

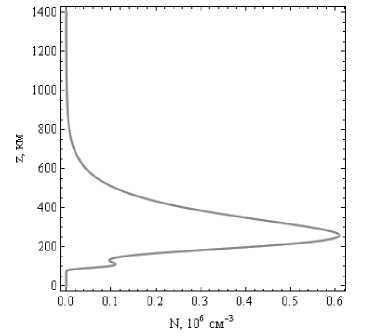
Рис. 1. Зависимость электронной концентрации от высоты в точке 40° с. ш., 30° в. д.

Методика вычислений

По аналогии с работами [2; 3] для определения траектории лучей используем би-характеристическую систему [7; 8]:

r dr аг dk _ ar dt _ ar dюдг ^^^^^^^^^^^^^^^^^™           ^^^^^^^^^^^^^^^^^^^^™        ______________ — ^^^^^^^^^^^^^^^^^^™       _____________ — ________________ ^^^^^^^^^^^^^^^^^^^^           ______________ r ,                       ,                        ,                     ,

dт дk  dт    дr dт    дю dт   дt

с гамильтонианом:

г = k x ² + k y ² + k² -Ю _е(r , k, ю ) .

В выражениях (1) и (2) k = ( k x ,k y ,k z ) - волновой вектор; r = ( x , y , z ) - координаты точки наблюдения; ю = 2 п f - круговая частота излучения; f - рабочая частота; t - групповое время; т - параметр вдоль лучевой траектории; е ( r, k , ю ) - эффективная диэлектрическая проницаемость среды распространения , с = 2,997 925·10⁸ м/с – скорость света (см. также [9–11]). Учитывая, что рабочая частота в данной задаче много

больше плазменной юp, можно считать, что r е г (r ,k ,ю) = 1

^^^^^^e

2 ^p ] ю J

а плазменная частота определяется формулой:

4 п e ² N ^ю р =------ m_e

.

В выражении (4) e = 4,802 9 10^–10 СГСЭ – заряд электрона; m_e = 9,108 10^–28 г – масса электрона; N – величина электронной концентрации в фиксированной точке пространства. r

Будем считать, что начальный волновой вектор k (0) параметрически зависит от угла выхода луча а ₀ :

kx (0) = — Telcos «о, ky, (0) = 0, kz (0) = — д/ё^т ao, (5) cc источник излучения точечный и расположен в точке с координатами (0, 0, zr). В выражениях (5) как ε0 обозначено значение эффективной диэлектрической проницаемости среды в источнике излучения.

Лучевые траектории

На рис. 2 показаны лучевые траектории в плоскости ( x , z ).

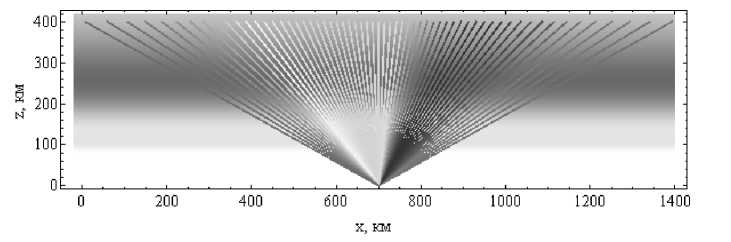
Рис. 2. Лучевые траектории на фоне профиля электронной концентрации ионосферы

Предполагается, что источник излучения расположен на высоте z_r = 400 км и горизонтально перемещается. При этом угол наклона лучей меняется от 150 до 30 градусов относительно положительного направления горизонтальной оси. Приемник расположен на поверхности Земли на расстоянии x_p = 700 км от начала координат. На рисунке выделены только те траектории, которые приходят в точку наблюдения. Серым цветом показано распределение электронов в ионосфере. Более темные области соответствуют более высокой электронной концентрации.

На рис. 3 приведена зависимость группового времени от координаты x источника излучения. Из рисунка следует, что зависимость квазипараболическая. Групповая задержка принимает минимальное значение под источником излучения.

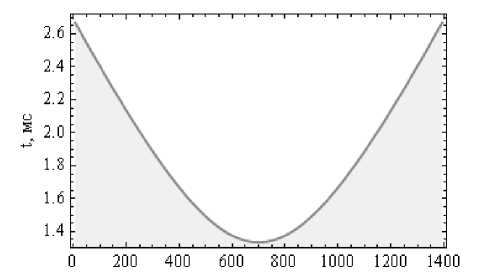
X, км

Рис. 3. Зависимость группового времени t от координаты x выхода луча

Необходимо отметить, что рис. 2 и 3 практически одинаковы для всех трех рассматриваемых частот и визуально не различаются. Все траектории на рис. 2 показаны как прямые линии. На самом деле они испытывают рефракцию при распространении в ионосфере и поэтому отклоняются от прямой линии. На рис. 4 а , б , в показано отклонение лучей вдоль траекторий по вертикали, рассчитанное по формуле (6):

x ( t ) - x„

A z = z ( t )-- z .                               (6)

x p ^- x ⁽ t r )

Здесь величина t_r – это групповое время прихода луча на высоту z_r . Видно, что вдоль траектории луч отклоняется на величину порядка длины волны, а затем в точке приема отклонение опять становится нулевым.

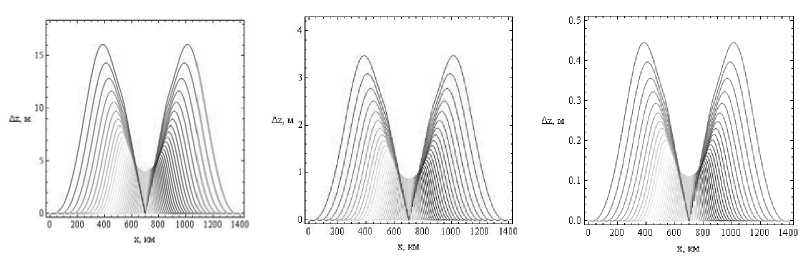
б

а

в

Рис. 4. Отклонение лучей по вертикали, а – 200 МГц, б – 430 МГц, в – 1 200 МГц

Видно, что если на частоте 1 200 МГц (длина волны ~25 см) максимальное отклонение не превышает 46 см, то на 430 МГц (длина волны ~63 см) – 3,6 м, а на частоте 200 МГц (длина волны ~1,5 м) максимальное отклонение не превышает 17 м. Таким образом, получается, что при увеличении частоты при одинаковых условиях отношение максимального отклонения к длине волны уменьшается.

Рассмотрим теперь (рис. 5) отклонение Δα угла прицеливания α от прямой линии:

Δα = α _n – Δα,                                (7)

В (7) α _n – это угол между прямой линией, соединяющей передатчик и приемник, и положительным направлением оси x , а α – угол между касательной к лучу в точке приема и положительным направлением оси x . Формулу (7) можно представить в виде

Δα = π – α _t – α,                                (8)

где угол α _t , дополнительный к углу α _n . Угол α _t определяется из соотношений:

x_n - x ( t, )

sin a, = - z_r IR, cos a, = —------- ,                    (9)

tr     t R где R = ^z2 + (xr - xp)2 - это расстояние между источником и приемником по прямой.

Из рис. 5 следует, что отклонение Δα незначительное и составляет для лучей, близких к крайним 30·10–3 град на частоте 200 МГц, 6·10–3 град на частоте 430 МГц и 10–3 град на частоте 1 200 МГц. Однако даже такое отклонение указывает на существенное изменение фазы вдоль луча и фарадеевское вращение вектора поляризации.

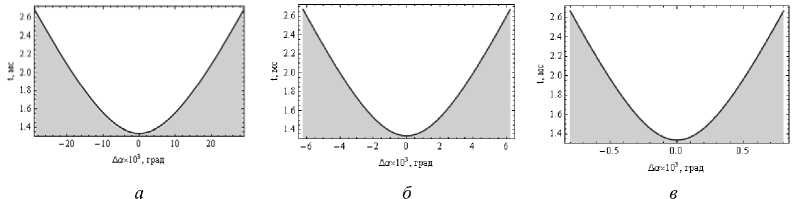
Рис. 5. Отклонение угла прицеливания от прямой линии, а – 200 МГц, б – 430 МГц, в – 1 200 МГц

Фазовые соотношения

Рассмотрим зависимость относительной скорости изменения фазы от высоты

(рис. 6). Производная фазы по групповому времени определяется формулой:

ф ; ( t ) = dX^x ( t ) + ^ky ( t ) + dzk z ( t ) -ю = Ф' ( t ) - ®           (10)

dt dt dt и в случае изотропной среды и плоскослоистой модели не зависит от траектории:

ф ; ( t ) = m ( _G ( z ( t )) - 1) .

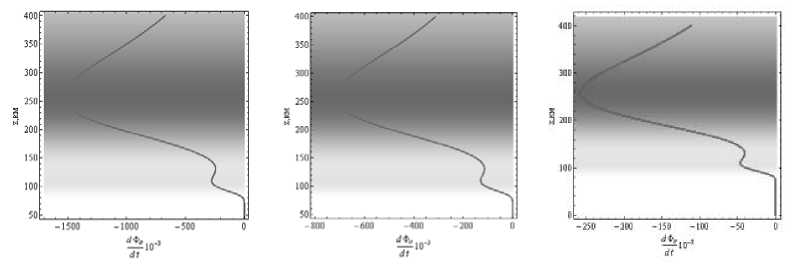
а                                б                              в

Рис. 6. Зависимость скорости изменения фазы от высоты, а – 200 МГц, б – 430 МГц, в – 1 200 МГц

На рис. 6 видно, что минимумы кривой коррелируют с положениями максимумов ионосферных слоев. Локальный максимум соответствует межслоевой долине. Минимальное значение производной составляет порядка –1 500·103 с–1 на частоте 200 МГц, –700·103 с–1 на частоте 430 МГц и порядка –260·103 с–1 на частоте 1 200 МГц.

На рис. 7 показана зависимость отклонения фазы (отложена по горизонтали) от группового времени (отложено по вертикали) в точке приема сигнала. Для вычисления фазы применялась формула:

Ф( t) = |ф‘(п)^ n.(12)

Разность фаз DF находилась как

АФ = Ф-ю R / c,(13)

где ю R / c - фаза луча в пустоте вдоль прямой, соединяющей источник и приемник.

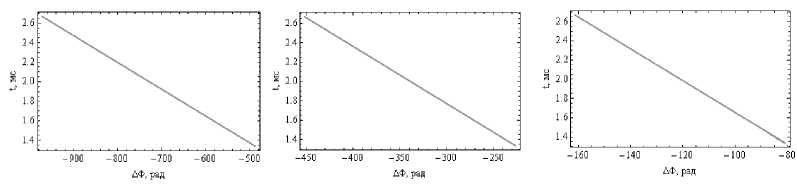
а                               б                                 в

Рис. 7. Зависимость отклонения фазы (по отношению к фазе в невозмущенной среде) от высоты, а – 200 МГц, б – 430 МГц, в – 1 200 МГц

Видно, что зависимость линейная, причем ионосфера вносит существенный вклад в величину фазы: на частоте 200 МГц – это от 83 до 167 периодов, на частоте 430 МГц – от 46 до 75 периодов, а на частоте 1 200 МГц – от 13 до 27 периодов.

Зависимость отклонения фазы от горизонтальной координаты x , соответствующей координате выхода луча, представлена на рис. 8. Форма кривой является квазипараболой. Наименьшее отклонение фазы соответствует вертикальному лучу.

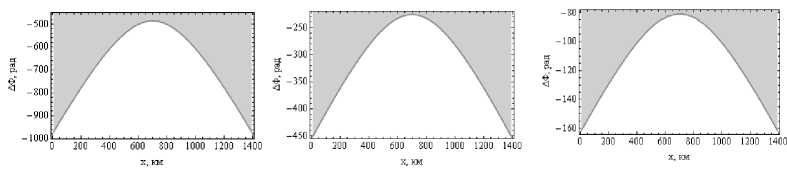
б

в

Рис. 8. Зависимость разности фаз (по отношению к невозмущенной среде) от расстояния по горизонтали, а – 200 МГц, б – 430 МГц, в – 1 200 МГц

Диапазоны отклонения разности фаз те же, что и на рис. 7.

Фарадеевское вращение плоскости поляризации радиоволны

Рассмотрим фарадеевское вращение плоскости поляризации, считая, что обыкновенная и необыкновенная волны в высокочастотном диапазоне распространяются вдоль одной и той же лучевой траектории. Согласно [12] (см. также [1–3; 13]), угол фарадеевского вращения определяется формулой:

Q ( t ) =

t22

го ( dx i    ( dy i

Ац I I +1 I +1

2 c 0   \d dt)   V dt)V

dt ,

в которой введено обозначение

1 v^u ² sin⁴ 6 + 4 ( 1 - v ) 2 u cos² 6

0 ) - u sin² 6

2 (1 - v ) ( 1 - u cos²

Ац - это разность показателей преломления обыкновенной и необыкновенной волны, а параметр u – это отношение квадрата гирочастоты к квадрату круговой частоты:

u =

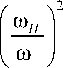
e ² H 0 ²

22 2 .

m e c го

Угол θ – это угол меrжду вектором напряженности внешнего магнитного поля H0 и волновым вектором k . В квазиизотропной среде можно приблизительно считать, что t

Q ( t ) = ГО ^ Ац^(r(t )) dt .                          (17)

В приведенных ниже расчетах амплитуда магнитного поля предполагается постоянной, а ориентация напряженности магнитного поля относительно локальной системы координат задается углами γ и φ:

H 0 x = H ₀cos Y cos Ф , H 0 y = H ₀cos Y sin Ф , H 0 z = H ₀sin Y •       (18)

При вычислении применялись следующие значения параметров: Н ₀ = 0,465 Э, γ = –57°, φ = 45°.

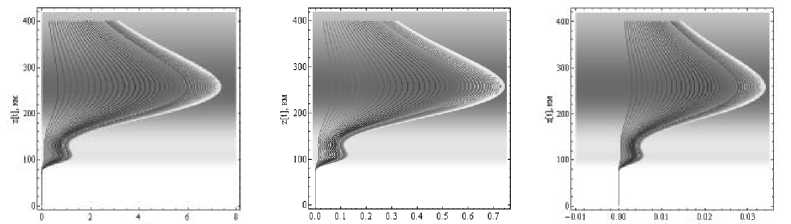
Зависимости разности Δμ показателей преломления обыкновенной и необыкновенной волны от высоты вдоль лучей при различных частотах приведены на рис. 9.

Дц х 10 6                              Дц х 10 6                            Дц х 10 6

а

б

в

Рис. 9. Зависимость разности показателей преломления обыкновенной и необыкновенной волны от высоты вдоль лучей, а – 200 МГц, б – 430 МГц, в – 1 200 МГц

Видно, что форма кривой отслеживает профиль электронной концентрации. Хотя форма кривых сохраняется для разных частот, при изменении частоты существенно меняется диапазон значений Δμ: на частоте 200 МГц достигает 7,5·10–6, на частоте 430 МГц – 0,75·10–6, а на частоте 1 200 МГц – 0,035·10–6.

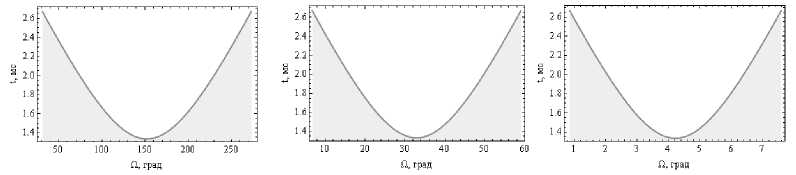
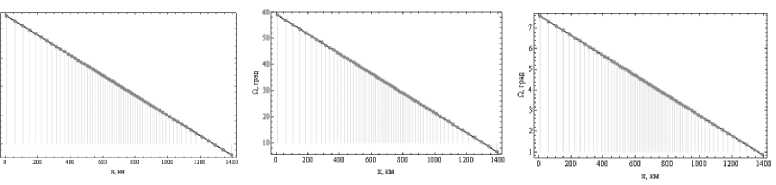
На рис. 10 показана зависимость угла фарадеевского вращения W (по горизонтали) от группового времени при различных частотах, а на рис. 11 – зависимость угла фарадеевского вращения от координаты x . Форма кривой на рис. 10 – квазипарабола.

а

б

в

Рис. 10. Зависимость угла фарадеевского вращения от группового времени, а – 200 МГц, б – 430 МГц, в – 1 200 МГц

а                                б                               в

Рис. 11. Зависимость угла фарадеевского вращения от расстояния по горизонтали, а – 200 МГц, б – 430 МГц, в – 1 200 МГц

Из рис. 10 следует, что угол фарадеевского вращения достигает 270° на частоте 200 МГц, 60° – на частоте 430 МГц и 8° – на частоте 1 200 МГц. Эти значения соответствуют координате x = 0 км (см. рис. 11). Следует отметить, что угол фарадеевского вращения при дальности x = 1 400 км (групповое время порядка 2,64 мс) минимален и составляет 30° на частоте 200 МГц, 7,5° – на частоте 430 МГц и 0,8° – на частоте 1 200 МГц.

Заключение

Таким образом, в работе методом бихарактеристик рассмотрены особенности влияния ионосферы Земли на распространение высокочастотных радиоволн: отклонение лучевых траекторий от прямых линий, изменение величины набега фазы за счет влияния ионосферы и фарадеевское вращение. Сопоставлены оценки величин угла фарадеевского вращения на частотах: 200 МГц, 430 МГц, 1 200 МГц.