Исследование влияния климатических факторов на скорость разложения лесной подстилки

«L^ §н

DOI:

Разложение лесной подстилки играет важную роль в общем цикле возникновения питательных веществ, а также накопления углерода в лесной среде. Этот процесс поддерживает природную динамику лесной экосистемы, играя важную роль глобальном балансе СО2 [2; 14; 15]. Связь между климатическими факторами и показателями декомпозиции лесной подстилки была исследована в работах [3; 5; 8]. При этом, согласно [8], климатические факторы воздействуют на процессы разложения подстилки как прямо, так и косвенно. С одной стороны, климат воздействует на бактерии и микроорганизмы, с другой стороны, приводит к качественным и количественным изменениям самой подстилки. В локальном масштабе факторами, воздействующими на процесс разложения подстилки являются влажность почвы, наличие питательных веществ в почве, озон, структура и содержание листьев, наличие осадков. Согласно [6; 13], скорость декомпозиции подстилки экспоненциально увеличивается с ростом температура почвы вплоть до некоторой оптимальной величины.

В общем случае, разложение подстилки меняет свои показатели под воздействием климатических изменений. Следовательно, с учетом влияния этого процесса на глобальный углеродный цикл, процесс декомпозиции представляет собой обратную связь, воздействующую на будущие климатические изменения.

Во многих работах, посвященных процессам декомпозиции лесной подстилки, воздействующие климатические факторы рассматриваются в качестве неизменных величин [4; 10]. Вместе с тем микроклиматические факторы достаточно изменчивы, что должно быть учтено при моделировании процессов разложения лесной подстилки.

В качестве примера рассмотрим, как учитываются климатические факторы в наиболее развитой модели декомпозиции подстилки, предложенной в работе [9]. Согласно этой модели, исходное органическое вещество ( M ₀) состоит из двух составляющих: лигнина ( М ₁) и целлюлозы ( M ₂). Следовательно,

M о = M о • (1 — to ) + M о • to , (1)

где M – долевой коэффициент.

При этом процесс декомпозиции лесной подстилки отображается следующей формулой:

M ( t ) = M 1 ∙ exp (– k 1 ∙ CDI ∙ t ) +

+ M 1 ∙ exp (– k 2 ∙ CDI ∙ t ), (2)

где M ( t ) – количество биомассы в лесной подстилке; M 1 = M 0 (1 - to ); M 2 = M ₀( to ); k 1 , k 2 - соответству-ющие скорости декомпозиции; CDI – климатический индекс декомпозиции.

Согласно [9], скорости декомпозиции k ₁ и k ₂ увеличиваются с ростом температуры и влажности.

k ₁, k ₂= f ( RWC ) ∙ f ( t ), (3)

где f ( RWC ) – показатель, зависящий от влажности почвы; f ( t ) – показатель, зависящий от температуры почвы.

В целом, как отмечается в самой работе [9], взаимосвязь температуры и влажности имеет достаточно сложный характер, тем более, что в указанной модели информация о влажности берется путем оценки достаточно общего вегетационного индекса – нормализованного разностного дифференциального индекса NDVI , склонного к насыщению при достаточно высокой степени развития растительности, когда другой, не менее распространенный растительный индекс-индекс листовой площади ( LAI ) показывает достаточно высокие значения.

Указанные недостатки модели, предложенной в работе [9] диктует необходимость разработки более адекватной модели, в которой можно было бы учесть сложную связь между такими главенствующими факторами как температура и влажность почвы.

Вместе с тем задача определения взаимосвязи температуры и влажности почвы при оценке их совместного воздействия на скорость декомпозиции лесной подстилки может быть сформулирована в несколько иной плоскости. Для исследователей экологии лесной экосистемы может стать не менее интересной такая постановка задачи: при каком взаимоотношении указанных факторов скорость декомпозиции может достигать экстремальных величин? Ниже нами предлагается методика, позволяющая решить указанный вопрос.

Результаты и их обсуждения

Следует отметить, что влияние температуры и влажности на процессы декомпозиции исследуется в течение нескольких десятков лет [1; 7].

Вместе с тем с учетом сформулированного выше подхода к решению задачи влияния климатических факторов на скорость декомпозиции наиболее подходящей известной моделью является модель, предложенная в работе [12]. Согласно этой работе, скорость декомпозиции лесной подстилки может быть вычислена по следующей формуле:

k = aexp(PT + P 2 T ²)(1 - exp(YP o ))     (4)

где Т – температура (в Цельсиях); P ₀– годичная величина осадков; α , β ₁, β ₂, γ – параметры модели.

В работе [11], где используется модель (4), взаимосвязь температуры и осадков учитывается путем проведения вероятностного анализа на основе трех различных предположений о структуре модели. Отметим, что при рассмотрении проблемы влияния указанных климатических факторов в плане решения экстремальной задачи достижения наивысокой скорости декомпозиции достаточно принять единственное предположение, ограничивающее возможности выбора функции связи между T и Р . В качестве такого целевого функционала можно рассмотреть следующее выражение:

T max

F₁ = J aexp(вТ + в ₂ T ² )(1 - exp(yP )) dT .   (5)

При этом подразумеваем выполнение следующих условий (предположений):

• 1.    Существует некоторая оптимальная функция

• 2.    Искомая оптимальная функция удовлетворяет следующему ограничительному условию

P = f ( T ) opt ,                      (6)

при которой функционал F ₁ достигает максимальной величины.

T max

F₂ = J p ( T ) dT = C 1 = const .         (7)

Варианты функций P ( T ) удовлетворяющих условию (7) приведены на рисунке.

С учетом (5) и (7) составим задачу безусловной вариационной оптимизации, целевой функционал F ₀ которой имеет вид

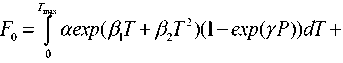
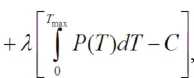
где λ – множитель Лагранжа.

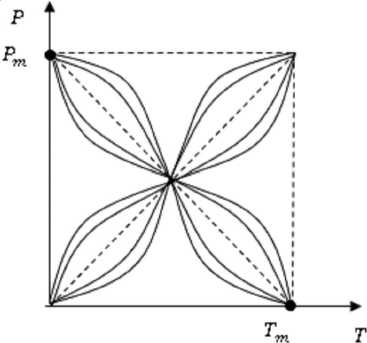
Примеры функций P ( T ), удовлетворяющих условию (7)

Решение оптимизационной задачи (8) согласно методу Эйлера должно удовлетворить условию:

d {aexp (PT + в2 T2) (1 - exp (y? (T))) + X? (T)} = 0 d? (T)

Из условия (9) получаем:

aexp ( P 1 T + P ₂ T "X- yexp ( y? ( T ))) + X = 0. (10)

Из выражения (10) получаем:

yexp (у? (T)) = ------- X          .(11)

(yaexp ( PT + 1 ₂ T ))

Из (11) получим:

? (T) =1 ln--------X------.(12)

’ у yexp(pxT + p2T2)

С учетом λ = const можно заключить, что при наличии обратнологарифмической связи между P ( T ) скорость декомпозиции лесной подстилки достигает экстремума.

Вычислим множитель Лагранжа. Из (12) находим:

? (T ) = —[ InX - ln[ yaexp ( P 1 T + P₂ T ²)]].   (13)

γ

Из (7) и (13) находим:

T m 1-YlniX - ln[ yaexp ( PT + p₂ T² )]] dT = 0. (14)

0 γ

Из (14) получаем:

T m ' l^{n y} = C - ¹ [ T m ln[ yaexp ( P , T + P ₂ T ²)] dT. (15) γ        γ ⁰

Из (15) окончательно находим:

T

γ 1m y = exp[yr[C - - j ln[yaexp(PT + P2T )]dT]].(16)

T_m     γ ₀

Чтобы определить тип экстремума целевого (16) функционала (8) достаточно вычислить вторую производную интегранта в (8) по P ( T ). Имеем:

d¹ ^aexp(P_xT + ^р₂Г² )(1 - exp(yP(Tp) + ЖГ?;

численной взаимосвязи рассмотренных климатических показателей.

Заключение

Важность исследования закономерности влияния климатических параметров на скорость разложения лесной подстилки объясняется особой ролью процессом декомпозиции подстилки в общем углеродном цикле в региональном и глобальном масштабе. Существующие подходы к решению данной задачи в основном основываются на вероятностном анализе взаимосвязи рассматриваемых климатических факторов. В отличие от указанных модельных исследований, автором предлагается представление решаемого вопроса в виде экстремальной задачи с учетом некоторого ограничительного условия налагаемого на искомую функцию взаимосвязи между температурой и влажностью почвы. Решение составленной вариационной задачи позволило вычислить оптимальный вид указанной взаимосвязи, при которой скорость разложения лесной подстилки достигает максимума. Полученное решение может быть использовано при моделировании процессов влияния климатических факторов на общий углеродный цикл по части лесной экосистемы.