Исследование влияния кристаллографической текстуры на кривые предельных деформаций листовых заготовок

В практике листовой штамповки стандартом для оценки условий начала локализованного образования шейки в процессе формообразования листового металла при различных видах нагружения (от одноосного растяжения, сдвига и плоской деформации до равноосного двухосного растяжения) стали кривые предельных деформаций (FLC) [1], которые впервые были использованы в работах [2,3].

Экспериментальное построение кривых предельных деформаций по-прежнему остается самым надежным способом прогнозирования разрушения материала. Однако, используемые

экспериментальные методы относительно трудоемкие и дорогостоящие, так как для их проведения необходимо специализированное оборудование, большое количество испытываемого материала [27]. При этом полученные результаты не всегда удается воспроизвести.

В связи с этим разработано множество моделей и подходов для теоретического построения кривых предельных деформаций, которые можно условно разделить на энергетические и кинематические [4]. Энергетические критерии [5-8] фактически предсказывают не момент разрушения заготовки, а ее несущую способность (максимальную нагрузку), что дает возможность их использования для прогнозирования пред-разрушающего состояния заготовки.

Кинематические критерии [9], в отличие от энергетических, предсказывают не максимальную несущую способность заготовки, а ее предельное деформированное состояние в момент локализации деформации, когда на большей части заготовки формоизменение останавливается. Наибольшее распространение среди кинематических методов получили методы Г. Свифта и Р. Хилла [10,11]. Оценка, достоверности данных методов показала, что метод Г. Свифта целесообразно использовать для построения кривой предельной деформации только для области, где обе главных деформаций в плоскости листа принимают положительные значения, а метод Р.

Хилла, где одна из деформаций имеет отрицательные значения. Таким образом, совместное применение данных методов позволяет теоретически построить кривую предельных деформаций [12].

В работах З. Марчиняка и К. Кучинского локализация деформаций объясняется тем, что она возникает в начальной геометрической неоднородности (канавке) на поверхности листа [13,14]. В более поздних работах [15-18] модель Марчиняка-Кучинского неоднократно совершенствовалась для того, чтобы учесть различные особенности поведения материала при пластической деформации, например, анизотропию свойств. Однако, основным недостатком всех этих моделей является условие наличия дефекта в виде канавки, размеры и расположение которого значительно влияют на результаты расчетов, кроме того, в большинстве случаев, для их нахождения требуются экспериментальные данные.

В последние годы широкое распространение получил модифицированный критерий предельного нагружения, предложенный П. Хора [19-24], в соответствии с которым достижение максимального усилия в процессе нагружения является необходимым, но не достаточным условием наступления разрушения. При локализации деформации в процессе формообразования происходит изменение деформированного состояния в области шейки на плоское, что приводит к возникновению дополнительных растягивающих напряжений, как раз и являющихся причиной разрушения деформируемой заготовки. Таким образом, модифицированный критерий предельного нагружения учитывает изменение деформированного состояния при локализации деформаций, что позволяет значительно повысить точность теоретического построения кривых предельных деформаций.

В данной работе на основании модифицированного критерия предельного нагружения и условия пластичности, учитывающего в явном виде параметры строения материала упругие константы кристаллической решетки и кристаллографическую ориентация структуры [25], разработана математическая модель для расчета кривых предельных деформаций.

РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Рассмотрим процесс двухосного растяжения прямоугольного листа из ортотропного материала в условиях плоского напряженного состояния ( О з = 0 ). Криволинейные координатные линии u и V выбраны так, чтобы они совпадали с траекториями главных нормальных напряжений О" 1 и о 2 , а также с главными осями анизотропии (рисунок 1).

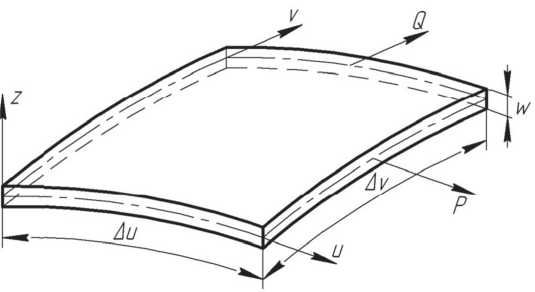
Рис. 1. Элемент листовой заготовки, находящийся в двухосном напряженном состоянии

Модифицированный критерий предельного

нагружения по П. Хора [19-24] записывается следующим образом:

д о ^ d r i д т ₈

~&^ d m j И^ = ¹ ,

где т ₈ - показатель деформационного состояния:

т ₈

где 8 1 и 8 2 - главные нормальные деформации д о  д о дт₈

Два слагаемых,---и 8, описывают д81   дт8 д81

приращение напряжений, вызванное упрочнением и изменением деформированного состояния на плоское соответственно. В процессе пластической деформации происходит увеличение напряжений из-за упрочнения материала, одна-д ко, скорость упрочнения —L уменьшается. При д81

д

условии —^L >  ° 1 , отношение деформаций не д 8 1

изменяется - т ₈ = const , а значит т ₈ = 0 .

_ д

Как только <  о , то деформированное со- д8 1     ¹

стояние т ₈ изменится. Очевидно, что влияние изменения отношения деформаций будет зави-

сеть от используемого условия пластичности.

Воспользуемся условием пластичности, разработанным в работе [25], которые для случая

плоского напряженного состояния в главных осях анизотропии запишется следующим образом:

° , = ^ V( ^ 12 ⁺ П 31 ) ^- 2 П 12 ^то ⁺ ( ^ 12 ⁺ П 23 ) ^та°"1; (3)

где т ° = О "1 / Г - показатель напряженного состояния; Пу — обобщенные показатели анизотропии:

П = ^{1 -}

15 ( A '- 1 ) 3 + 2 A

А, + А у

-А k

A - параметр анизотропии кристаллической решетки:

S I 111 - SH22

² S 2323

S jkl — константы кристаллической решетки; A _t - ориентационные факторы кристаллографиче

ской ориентировки:

A _ hik2 + k2li +12hi i 2222

( h i + ^ki + l i )

5 ^o 1         2 «                             tTj

— ^_--------- ^L ⁿ 12 ^m 8 ^{+ (n} 12 ⁺ 7 23 ) J— . ⁽¹⁴⁾

^{d 8} 1    7 12 7 23 7 31 N                        ⁸ i

Дифференцируя уравнения (10) и (2), распишем второе слагаемое в критерии П. Хора (1): Ю. ^d т _ ₂ °.m 2 (15) 5 ^m 8 8⁸ 1      ⁸ i ( П 12 + П 31 ) ^m 8 + 2 7 12 ^m 8 ⁺ ( 7 12 ⁺ 7 23 )

h i , k i , l i - индексы Миллера, определяющие i -е направление в кристалле относительно системы координат, связанной с листом.

Выражения для интенсивности деформаций и главных деформаций имеют вид:

Окончательно, подставляя выражения (14), (15) и (10) в критерий (1), определим предельную интенсивность деформаций:

кр _ яУ ( 7 12 ⁺ 7 31 ) m ^{2 + 2} 7 12 m e + ( 7 12 ⁺ 7 23 ) г

+•

V 7 12 7 23 7 31 ^N

ПиПаП зх Nm j

1 (16)

8 i = V2

V⁽ 7 12 ⁺ 7 31 ^{) -} 2 7 12 m g ^{+ (} 7 12 ⁺ 7 23 ) m o

[ ( 7 12 ⁺ П з1 ) m ^ + ² 7 12 m _E ⁺ ( П 12 ⁺ П 23 ) ] [ 7 12 P ⁺ ( 7 12 ⁺ П 23 ) ]

( 7 12 ⁺ П 31 ) ^- 7 12 m o

8 1 ; (7)

е _ 1           (712 + 731)- 712mo

• ⁸1    ^_~r^ I                                        ₂⁸i ’

  ^V2 V( 7 12 ⁺ 7 31 ) - 2 7 12 m o ⁺ ( П 12 ⁺ 7 23 ) mo

_ _ 1           (712 + 723 )mo - 712_

• 82          I

  ^V2 V( 7 12 ⁺ 7 31 ) - 2 7 12 m o ⁺ ( П 12 ⁺ 7 23 ) mo

Подставляя (16) в (11) с учетом (2), определим предельные деформации по П. Хора:

е ^кр _ n +

1        2                     (17)

₊______________________ 7 12 7 23 7 31 ^Nme ______________________,

[⁽ 7 12 ⁺ 7 31 ) m ^{2 + 2} 7 12 m e ⁺⁽ 7 12 ⁺ 7 23 ) ] [ 7 12 Р ⁺⁽ 7 12 ⁺ 7 23 ) ]

е^кр _ m _ee ^кр .

Подставляя уравнения (8) в соотношение (2) получим уравнения связи между показателями напряженного m _o и деформированного т ₈ состояний:

_т _ ⁽ « 12 ⁺ « 23 ) m o ^- « 12 ₍₉₎ ^{8 (} « 12 ⁺ « 31 ) ^- « 12 m o

Расчет т 8 в уравнениях (17) осуществляется по зависимости (9) для заданных значе-

ний т_а . Выражения (17) позволяют построить кривую предельную деформации на отрезке

^m o ^G [ ^0,1 ]

с учетом кристаллографической

ориентации структуры материала.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Используя зависимость (9), преобразуем выражения (3) и (7) к виду:

4 П 12 П 23 П 31N V( 7 12 ⁺ П 31 ) ^m 8 ⁺ 2 7 12 ^m 8 ⁺ ( П 12 ⁺ 7 23 ) oi _ ----- г-------------------;---------;----------o 1 ,

V 2                П 12 ^m 8 ⁺ ( П 12 ⁺ 7 23 )

⁸ i ^_ I            V( 7 12 ⁺ 7 31 ) ^m 8 ⁺ 2 7 12 ^m 8 ⁺ ( П 12 ⁺ П 23 ) ⁸ 1 .

V 7 12 7 23 7 31 N

(11) Распишем первое слагаемое в критерии

П. Хора (1) следующим образом:

d o i   d o i d o,- д8

---¹ _--- ¹--- ^L---^L,       (12) 5 8 1    d o i- d8 i 5 8 1

Примем, что упрочнение материала описывается степенной функцией:

o i _ K 8 i ,           (13)

где K и « - константы анизотропного материала.

После дифференцирования выражений для интенсивности напряжений (10), интенсивности деформаций (11) и степенной функции упрочнения (13) первое слагаемое в критерии П. Хора примет вид:

Для листовых материалов характерны определенные преимущественные кристаллографические ориентировки. Так после прокатки сплавов с кубической решеткой преобладают следующие ориентировки деформационного типа: {112}<111> (медь), {110}<112> (латунь), {123}<634> (S) и {100}<011> («куб на ребре»). В отожженных листах преимущественными являются ориентировки рекристаллизационного типа: {100}<001> (кубическая) и {110}<001> (Госса). При этом доля конкретных ориентировок определяется режимами прокатки и термической обработки.

Рассмотрим лист из меди, для которого компоненты тензора податливости S ji равны: 5 1'111 _ 15.0 ТПа^-1; S 1₁₂₂ _- 6.30 ТПа^-1 and S 2323 _ 3.33 ТПа^-1, тогда по формуле (5): A '_ 3.203 . Для указанных идеальных кристаллографических ориентировок по формулам (4) и (6) рассчитаны обобщенные показатели анизотропии (таблица 1).

На рисунке 2 показаны кривые предельных деформаций для различных кристаллографических ориентировок (таблица 1) при « _ 0,35 . Из рисунка 2 видно, что при т ₈ <  0 ориентировкой, обеспечивающие наивысшие деформационные возможности, является {110}<001>, но при т ₈ >  0

Таблица 1. Ориентационные факторы и обобщенные показатели анизотропии идеальных кристаллографических ориентировок

Кристаллографическая ориентировка		Ориентационные факторы			Обобщенные показатели анизотропии
Наименование	{ hkl }< uvw >	А 1	Д 2	Д 3	П 12	п 23	П 31
Медь	{112}<111>	0,333	0,250	0,250	0,533	1,116	0,533
Латунь	{110}<112>	0,250	0,333	0,250	0,533	0,533	1,116
S	{123}<634>	0,281	0,278	0,250	0,617	0,835	0,814
«Куб на ребре»	{100}<011>	0,250	0,250	0,0	-0,054	1,703	1,703
Кубическая	{100}<001>	0,0	0,0	0,0	1,703	1,703	1,703
Госса	{110}<001>	0,0	0,250	0,250	1,703	-0,054	1,703
Изотропный случай		0,20	0,20	0,20	1,0	1,0	1,0

данная ориентировка показывает самые низкие предельные деформации. Аналогичная картина наблюдается и для некоторых других рассматриваемых ориентировок. Например, ориентировка {100}<011> обеспечивает наивысшие деформационные возможности при m _g >  0 , но при m _g <  0 - все наоборот. Кривые для изотропного случая и кубической ориентировки совпадают.

В отличии от метода Р. Хилла и Г. Свифта [26], метод П. Хора позволяет построить обе ветви кривой предельной деформации, при этом в области m _g <  0 учитывается влияние кристаллографической ориентации структуры.

Сравнивая кривые предельных деформаций для различных ориентировок, можно увидеть, что дополнительные напряжения, возникающие вследствие изменения деформированного состояния на плоское, могут приводить как к увеличению (например, ориентировка {100}<011>, правая ветвь кривой), так и уменьшению предельных деформаций ({110}<001>) по сравнению со случаем, когда учитывается только упрочнение. Влияние дополнительных напряжений определяется не только кристаллографией структуры материала, но и деформированным состоянием.

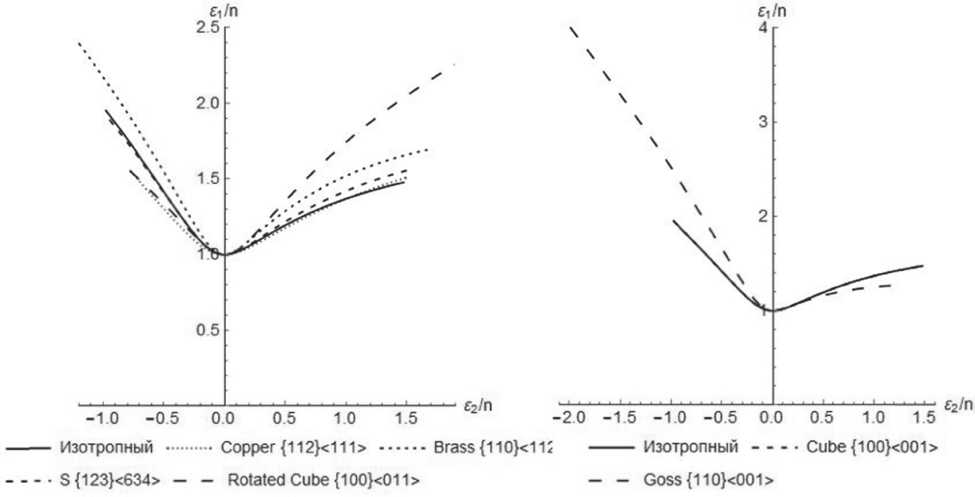
а

б

Рис. 2. Кривые предельных деформаций по методу П. Хора для идеальных кристаллографических ориентировок деформационного (а) и рекристаллизационного (б) типов

ЗАКЛЮЧЕНИЕ

В данной работе были построены кривые предельных деформаций материала на основе критерия П. Хора с учетом условия пластичности, учитывающего кристаллографию структуры материала. Однозначно назвать ориентировку, обеспечивающую наилучшие деформационные возможности невозможно, так как предельные деформации зависят от напряженно – деформированного состояния вызванному, конкретной технологической операцией листовой штамповки. Так при линейном растяжении наилучшие показатели у ориентировки деформационного типа, при двухстороннем растяжении – у ориентировок рекристаллизационного типа. Таким образом, при производстве листовых заготовок необходимо назначить согласованные режимы прокатки и промежуточной термической обработки (отжига), обеспечивающие формирование заданных идеальных кристаллографических ориентировок, необходимых для повышения предельных деформаций в конкретных операциях листовой штамповки.

Исследование выполнено в рамках госзада-ния (тема FSSS-2020-0016).