Исследование влияния кривизны передней поверхности на прочность лезвия инструмента

Для криволинейной передней поверхности длина пластического и полного контакта стружки с инструментом равна [1]:

l0=0,5 l l = «1У2[1 -(ajRu)0"1 exp(-3,96a, /Ru)] sin /^sin^/4 + в1-Y)        ’ (1)

где R u – вертикальный радиус завивания; а 1 – толщина срезаемого слоя; β 1 – угол наклона условной поверхности сдвига; γ – передний угол инструмента.

Расчеты по (1) и их сопоставление с экспериментальными данными показывают, что данная зависимость может быть использована как для вогнутых, так и для выпуклых форм передней поверхности. В зоне пластического контакта стружки с передней поверхностью режущего клина касательные напряжения распределены равномерно и равны пределу текучести на сдвиг τ Р . За пределами участка l 0 величина касательных напряжений уменьшается и в точке отрыва стружки D равна нулю. Согласно работе [2] характер уменьшения величины касательных напряжений можно принять линейным. Тогда зависимость величины касательных напряжений от координаты х (рис. 1) будет иметь вид:

т = 2 т_p

1 —

I l J

при x >  1 ₀.

Нормальные контактные напряжения имеют максимальное значение у вершины режущего клина [2]:

^max = 2Tр (1,385 + Ypad Y

Распределение нормальных напряжений на передней поверхности лезвия резца задается по зависимости:

OB = p£

arccos 1 -V

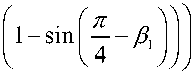
^N = ^max 1 —J .

V l 7           (4)

Показатель n в формуле (4) равен:

<7 bl

П = max I _ 1, P РN                  (5)

OB = Р £

arccos 1 -

OB = Р £

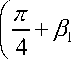
1 - cos

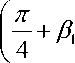
где b 1 – ширина срезаемого слоя; P N – нормальная составляющая силы стружкообразо-вания, действующая перпендикулярно передней поверхности резца (рассчитывается через тангенциальную составляющую силы резания P z ).

В процессе резания отделение металла срезаемого слоя толщиной а 1 и его переход в стружку происходит по линии OM . Слой металла толщиной h п.с. подминается под заднюю поверхность резца. На выходе из контактной зоны материал упруго восстанавливается на величину h упр =h п.с. –h пл , где h пл – доля пластической деформации подминаемого слоя. В т. О – границе между передней и задней поверхностью режущего клина касательные напряжения равны нулю. Согласно известному положению из теории линий скольжения, линии максимальных касательных напряжений в зоне резания выходят на поверхность инструмента в т. О под углом 45º. Для схемы резания с единственной плоскостью сдвига указанное свойство линий скольжения будет выполняться, когда плоскость сдвига образует с касательной к радиусу округления режущей кромки угол п/4 [3]. Из приведенных рассуждений следует:

Длина участка AB может быть вычислена по формуле:

AB = Р£

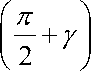
На радиусном участке OA касательные напряжения возрастают от 0 до τ Р Аналогично изменяются касательные напряжения на участке ОВ режущей кромки Характер увеличения касательных напряжения принимаем линейным Нормальные напряжения на радиусном участке резца распределены равномерно и равны σ max Контакт заготовки с задней поверхностью режущего клина по участку EF возникает вследствие упругого восстановления материала подминаемого слоя (рис 2)

sin--01

L = р£

= Р _£   h n . с .

Р £

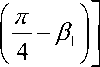
= 1 _

h

Р _£

;

Зная h п.с. , длина участка ОВ определится по

формуле:

OB = р£

arccos

V   р£ 7

где ρ ε – радиус округления режущей кромки; h п.с. – величина подминаемого слоя

Формула (7) с учётом (6) может быть преобразована:

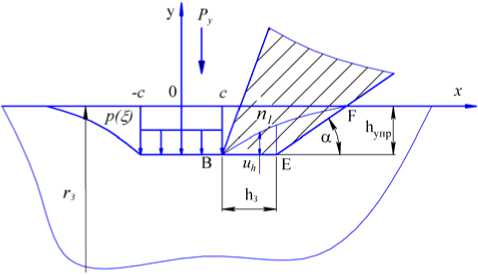
Рис. 2. Схема к определению величины h упр [4]

Движущаяся перед резцом пластическая область сопровождается волной упругой деформации, что приводит к опусканию границы полуплоскости на величину h упр При этом восстанавливающаяся позади режущей кромки поверхность Bn 1 F взаимодействует с плоскостью фаски, дополнительно деформируясь до положения BEF Выражение для определения величины h упр имеет вид [4]:

hynp = Py г 2 сln 2 с - сln( с2 + r2) + ГЗ (и - 1) arctg с" , nb1 сЕ L                                     гЗ где Py – радиальная составляющая силы

стружкообразования; b 1 – ширина срезаемого слоя; r З – радиус заготовки; υ , Е – коэффициент Пуассона и модуль упругости обрабатываемого материала; с – половина длины напряженного участка [ -с; с ], равная проекции условной поверхности сдвига на границу полуплоскости:

с = 0,5 a 1 ctg P 1 ,

где a 1 – толщина среза; β 1 – угол наклона условной поверхности сдвига.

Длина участка EF определяется из выражения:

EF = h ynp ^/sin « ,

где α – задний угол резца.

Согласно [2] можно принять, что на участке EF касательные напряжения линейно уменьшаются от точки Е , где имеют максимальные значения, до т. F , где равны нулю (см. рис. 1). Анализ теории деформирования и разрушения твердого тела показывает, что методика расчета прочности лезвия инструмента со сложной передней поверхностью может быть создана на основе численных методов расчета напряжений в твердом теле. В настоящей работе оценка прочности режущего клина осуществлена с помощью метода конечных элементов, который реализован в системе ProMechanica, входящей в состав программы ProEngineer.

Процесс моделирования прочности контактной зоны инструмента осуществлялся в следующей последовательности. Строился эскиз фронтального профиля режущего клина, с помощью которого создавалась трехмерная модель резца. Определялось положение заделки лезвия резца. Активная часть режущей поверхности разбивалась на регионы, к которым прикладывались контактные нагрузки (рис. 4). Физико-механические свойства модели резца соответствовали твердому сплаву Т15К6: плотность – 11900 кг/м3, модуль упругости – 540 ГПа, коэффициент Пуассона – 0,06, коэффициент линейного расширения – 6*10-6. Напряжения, действующие на каждом из выделенных регионов, рассчитывались по составляющим силы резания, найденным экспериментальным путем. С этой целью разработан алгоритм и программа определения координат границ регионов и их проекций на координатные оси для различных форм режущих клиньев (рис. 3).

Для определения границ регионов получены следующие зависимости:

• -    для вогнутой передней поверхности:

  

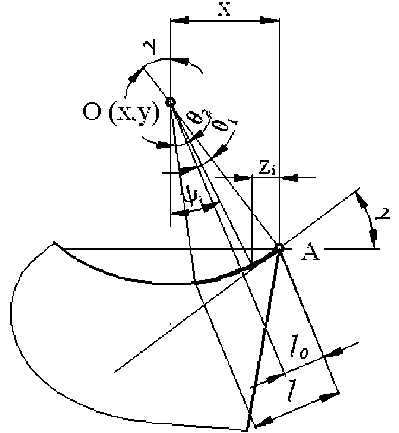
  Рис. 3. Схема к определению границ проекций регионов

  
  

x = r sin y

при у > 0, yi = у -iAy, zi = x- r sinyi

при y ^ 0, yi = iAy - y, zi = r sinyi + x ,

• -    для выпуклой передней поверхности:

x = - r sin y

при y ^ 0, yi= y + iAy,  zi = x + r sin yi

при y < 0, yi = -iA y - y, zi = x - r sin yi где r – радиус вогнутой/выпуклой передней поверхности; i – номер региона.

После задания всех нагрузок расчетная схема примет вид, показанный на рис. 4.

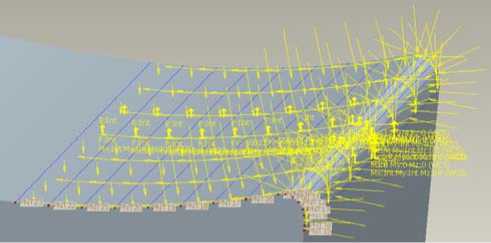
Рис. 4. Схема нагрузок в режущем клине (ProMechanica).

Результаты расчета напряженного состояния резцов с различной геометрией представлены на рис. 5. Расчеты выполнены для следующих условий: ν =1 м/с, s =0,3 мм/об, t =3 мм, φ =90º, φ 1 =3º, γ =15º, α =6º, ρ ε =0,1 мм, h з =0,05 мм, сталь 45–Т5К10, поперечное точение.

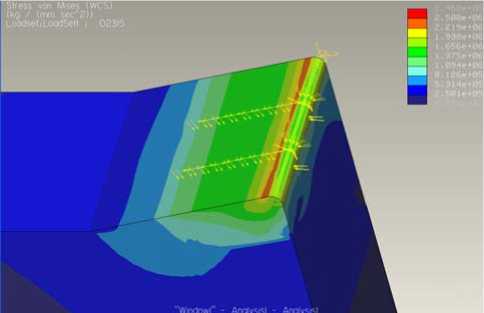
а)

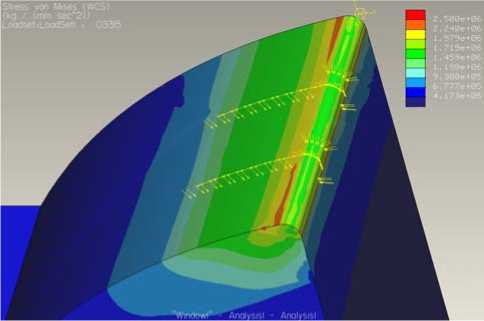
б)

Рис. 5. Напряженное состояние плоского режущего клина (а) выпуклого режущего клина с

Выводы: при использовании резцов с выпуклой передней поверхностью максимальные напряжения перераспределяются и режущая кромка разгружается. В результате прочность резца с выпуклой поверхностью по сравнению с плоской возрастает, несмотря на уменьшение среднего значении угла заострения.