Исследование влияния локальных неоднородностей ионосферной плазмы на распространение коротких радиоволн

Настоящая работа посвящена исследованию влияния локальных неоднородностей ионосферы на особенности распространения радиоволн и продолжает работы [1–4], в которых методом би- характеристик было исследовано распространение электромагнитных волн в неоднородной ионосфере с учетом влияния магнитного поля Земли, а также рассмотрены особенности распространения обыкновенной и необыкновенной составляющих электромагнитного поля как с учетом, так и без учета кривизны поверхности Земли на односкачковых и многоскачковых трассах. Актуальность исследования распространения электромагнитных волн в ионосферной плазме определяется необходимостью решения задач радиолокации, дальней радиосвязи, радионавигации, а также необходимостью диагностики структуры среды распространения: тропосферы, ионосферы или магнитосферы. Традиционными методами исследования распространения радиоволн в ионосфере Земли являются лучевые подходы, наиболее важным из которых является метод бихарактеристик, разработанный Д.С. Лукиным [5].

В работе [5] показано, что бихарактеристи-ческую систему уравнений можно представить в

виде:

8К _ дю^S | дю^S 8т д ре I д ю

8р L 2 -

_ 2 X к - 8т l

дю2 s || дю2 s д К А д ю

где k _ ( k_x , k y , k z ) - волновой вектор;

r _ ( x , y , z ) - координаты точки наблюдения;

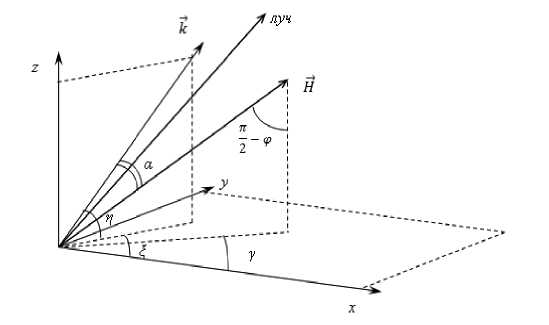
Рис. 1

ω – круговая частота излучения;

с = 2,997925∙10¹⁰ см/с – скорость света;

t - параметр вдоль лучевой траектории;

; = ; ( r, k , ю ) - эффективная диэлектрическая

где функции:

F , ^{( x} , У , ^z ) ^_

^{_ e} loc exp

проницаемость среды распространения.

Для магнитоактивной среды эффективная диэлектрическая проницаемость может быть представлена в виде (см., например [6, 7]):

2 v (1 - v )

^Е ± = ¹--;------- / 2 2                 2     2 , (2)

2(1 - v ) - u sin а ± ум sin а + 4 и (1 - v ) cos а

юР  4пе2 N где v_—1-_----—,

ю   meю

ю .     e² H 0

u 2        2 2   2 , ю   me сю

e = 4,8029∙10^–10 СГСЭ – заряд электрона;

m_e = 9,108∙10^–28 г – масса электрона;

H ₀ – абсолютная величина напряженности магнитного поля Земли;

N – профиль электронной концентрации.

Угол α – это угол между волновым вектором и

в е ктором напряженности магнитного поля Земли H о _ ( H _{0 x} , H _{0 y} , H ₀ z ). Следовательно:

cos а _

^{^} 0 x^kx ^{+ ^} 0 y^ky ^{+ ^} 0 z^kz h 0 i k

Знак «+» соответствует обыкновенной волне,

а знак «–» – необыкновенной волне.

Предполагается, что источник излучения точечный, расположен в начале координат ( ^е (0) _ 0), причем начальный волновой вектор параметрически зависит от углов выхода луча (см. рис.1):

k_x (0) _ — cos Z cos n , k y (0) _ — sin Z cos n , c . ю. c             (5)

k z (0) _ —sin n .

c

В данной работе рассмотрено коротковолновое распространение в случае, когда профиль электронной концентрации двухслойной ионосферной плазмы имеет вид:

ц

N ( r ) _ N 0 ^ N f + e N e + £ F, ( x , y , z ) [ ,   (6)

I                                            , _ 1                                 I

x - x/oc I xm з  J

У - У ос I . y m з J

z -

zlioc

описывают локальные неоднородности эллипсоидальной формы среды распространения, величина

N E ^_ exp2

z - z 02

V z m 2 / ² J

sec x exp

z - z 02 l Z m 2 /2

JI

– это нормированное значение электронной концентрации слоя Е , а величина

^

N_f _ exp

z

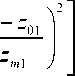
нормированное значение электронной концентрации слоя F ₂.

Здесь:

z01 – высота максимума основного слоя F2, zm1 – условная полутолщина основного слоя F2, z02 – высота максимума нижнего слоя Е, zm2 – условная полутолщина нижнего слоя Е, (расстояние от высоты максимума вниз, на котором электронная концентрация падает в e раз);

β – безразмерный коэффициент, характеризующий степень ионизации нижнего слоя по отно-

шению к основному;

N ₀ – электронная концентрация в максимуме основного слоя.

В работе, если не оговорено иное, при численном моделировании применялись следующие значения перечисленных выше параметров: N 0 = 2-10 6 см ^{- 3}, H 0 = 0,36 Э, z m 1 = 100 км, z m 2 = = 10 км, z ₀₁ = 300 км, z ₀₂ = 100 км, Z = 0, x = 0. Таким образом, предполагалось, что изначально распространение осуществляется в плоскости ( x , z ). В настоящих расчетах амплитуда напряженности магнитного поля предполагалась постоянной, а ориентация относительно системы координат задавалась двумя углами γ и φ :

H 0 x = H 0 cos Y cos p , ^H 0 У = ^H 0 ^cos Y sin Ф , (10) H о _z = H o sin Y ^.

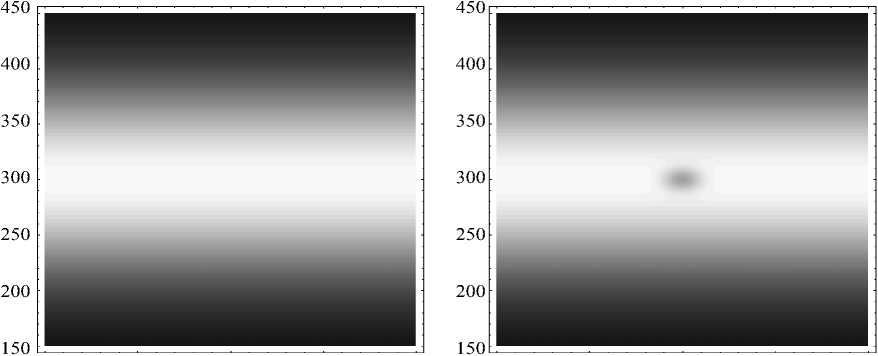
Рассмотрим результаты численного моделирования. На рис. 2 показано модельное распределение электронной концентрации по высоте в ионосферном плазменном слое (β = 0) при отсутствии (а) и наличии (б) локальной неоднородности.

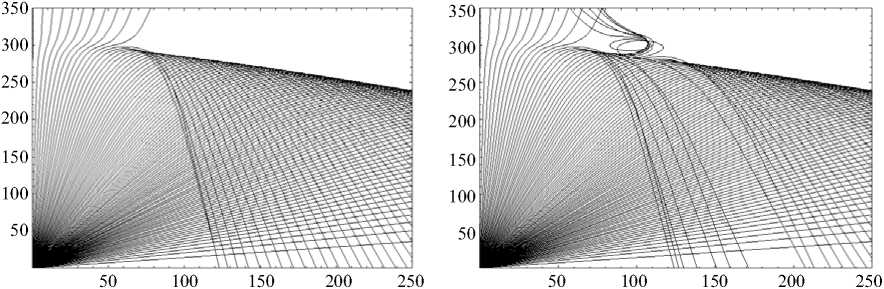
На рис. 3 приведен результат моделирования лучевой структуры в плоскости ( x , z ) в случае распространения необыкновенной волны при отсут-

Электронная концентрация                  Электронная концентрация z, км                                             z, км

0        50       100       150      200       0        50       100       150      200

x , км                                            x , км

Рис. 2а                                                              Рис. 2б

ствии локальных возмущений. Часть лучей при углах падения, близких к вертикальному, проходит ионосферный слой, а остальные возвращаются на Землю и образуют каустическое острие. Здесь направление вектора напряженности магнитного поля определяется углами γ = 3 π /4 и φ = π /2.

При возникновении локальной области пониженной электронной концентрации (в расчетах выбраны параметры μ = 1, xm3 = ym3 = zm3 = 10 км) на высоте максимума слоя (xloc = 100 км, zloc = = 300 км, yloc = 0, βloc = –0,3) возникает возмущение лучевой структуры (рис. 4). На рисунке видно, что неоднородность заставляет луч огибать себя не- сколько раз. При этом на Земле образуется дополнительная область «мертвой зоны».

На рис. 5 и 6 сопоставлены лучевые структуры в проекции на плоскость (y, z), образующиеся в невозмущенном (рис. 5) и возмущенном случаях (рис. 6). Если бы магнитное поле отсутствовало, все лучи в этой плоскости соответствовали бы линии y = 0. При наличии магнитного поля лучи отклоняются влево, а после выхода из ионосферы движутся вдоль оси y, но уже со смещением. Из сравнения рисунков видно, что неоднородность нарушает регулярность лучевой структуры, и поскольку луч огибает неоднородность, прежде чем z, км

z , км

Необыкновенная волна:

13,25 мГц; в = 0; Y = 135 град

Необыкновенная волна:

13,25 мГц; в = 0; Y = 135 град

x, км x, км

Рис. 3

Рис. 4

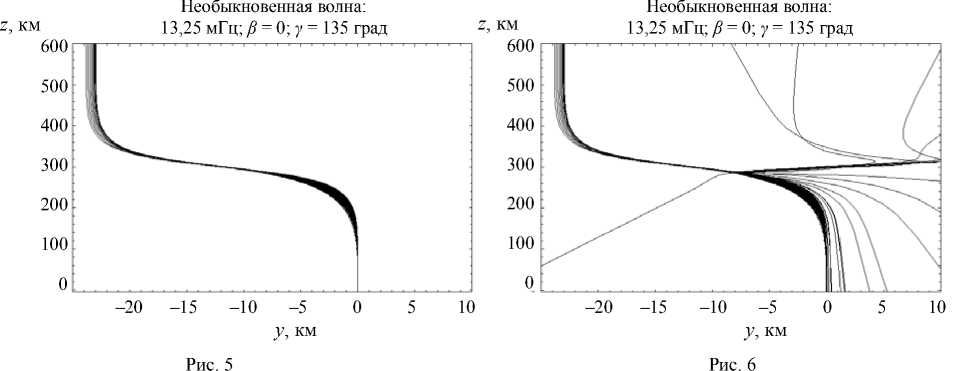
продолжить свой путь, он отклоняется в самых различных направлениях.

На рис. 7 и 8 показаны лучевые структуры в горизонтальной проекции, то есть в плоскости (x, y) в невозмущенном и возмущенном случаях, соответственно. Видно, что в невозмущенном случае лучи в этой плоскости также образуют каустическое острие, как и на рис. 3. В возмущенном случае луч не только выходит из плоскости распространения (рис. 7), но вращается в плоскости (x, y) (рис. 8), как и на рис. 4.

На рис. 10–12 показана лучевая структура необыкновенной волны в случае, когда угол γ = π/4, а в ионосфере имеются три разнесенные друг относительно друга сферические локальные неоднородности. Геометрические параметры неоднород- y, км

y , км

Необыкновенная волна: 13,25 мГц; в = 0; Y = 135 град

Необыкновенная волна: 13,25 мГц; в = 0; Y = 135 град

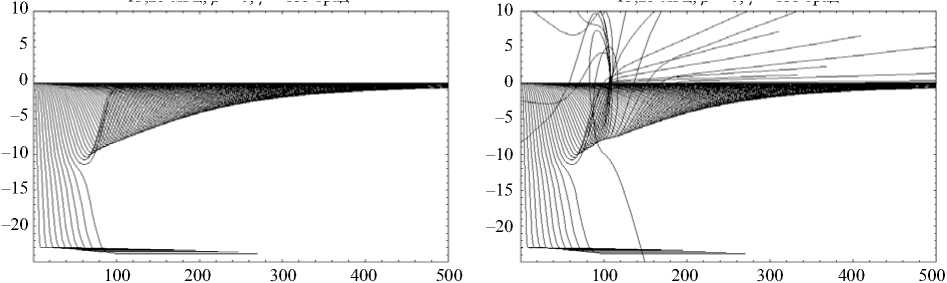
x , км Рис. 8

x , км

Рис. 7

Электронная концентрация

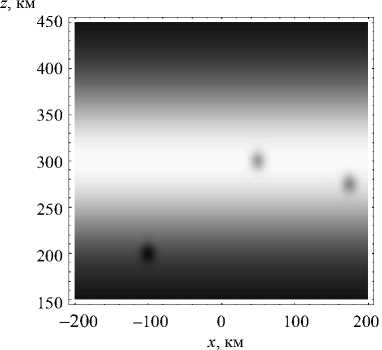
Рис. 9

Необыкновенная волна:

13,25 мГц; β = 0; γ = 45 град

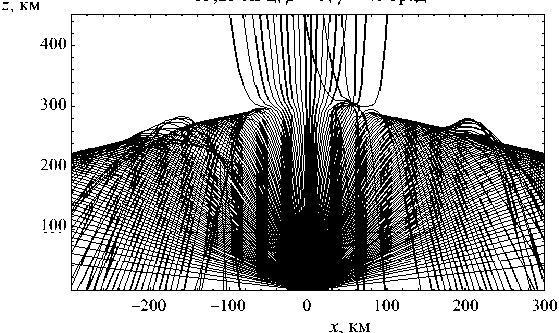
Рис. 10

ностей были выбраны такие же, как и выше, а центры расположены в точках с координатами (50 км, 0 км, 300 км), (175 км, 0 км, 275 км) и (–100 км, 0 км, 200 км), соответственно (см. рис. 9).

Рассмотрим результаты моделирования лучевой структуры в этом случае. В плоскости ( x , z ) центральная неоднородность стягивает лучи в «узел» (рис. 10), а боковые неоднородности формируют дополнительные каустические структуры

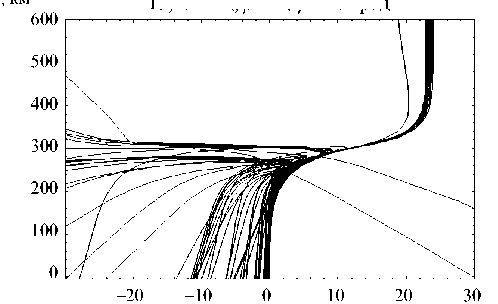
(«горбы») на левой и правой ветвях внешних каустик. Рис. 11 [проекция на плоскость ( y , z )] аналогичен рис. 6, но следует отметить, что он как бы зеркально отражен относительно вертикальной оси. Это объясняется изменением направления магнитного поля: предыдущий случай относился к южному полушарию, а настоящий случай – к северному. На рис. 12 показана лучевая структура уже в проекции на плоскость ( x , y ).

z

Необыкновенная волна:

13,25 мГц; β = 0; γ = 45 град

y , км

Рис. 11

Необыкновенная волна:

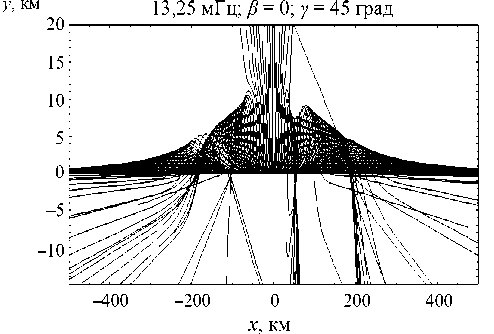
Рис. 12

Рис. 13–15 представляют лучевую структуру обыкновенной волны при тех же параметрах неоднородностей и той же рабочей частоте. Следует отметить, что лучевая структура вместе с каусти- ками как бы подтянулась вверх (рис. 13), причем доля лучей, проходящих ионосферу, заметно увеличилась. Качественно изменилась лучевая структура в плоскости (x, y) (рис. 15).

z , км

Обыкновенная волна:

13,25 мГц; β = 0; γ = 45 град

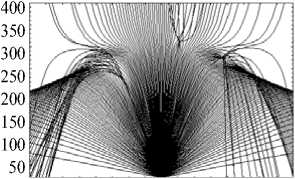
–200     0     200     400

x , км

Рис. 13

Необыкновенная волна:

13,25 мГц; β = 0; γ = 45 град z, км

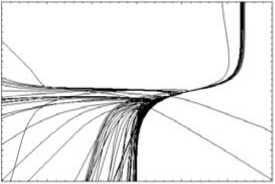
–20 –10    0    10   20   30

y , км

Рис. 14

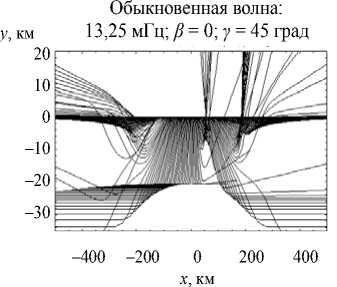
Рис. 15

Рассмотрим случай, когда локальные неоднородности присутствуют в двухслоевой модели ( β = 0,4). На рис. 16 представлены линии равного уровня модельной электронной концентрации с включенными неоднородностями, центры которых расположены в точках с координатами (165 км, 0 км, 105 км) и (100 км, 0 км, 290 км).

На рис. 17–19 показана лучевая структура поля необыкновенной волны в случае, когда все лучи отражаются от ионосферы, поскольку рабо- чая частота равна 13 МГц. Видно (см. рис. 17 и 18), что в плоскости (x, z) над каустикой возникает область, где лучи «наматываются» на неоднородность («петли» лучей), причем они наматываются на неоднородность не только в одной плоскости, а как нитки на клубок [см. рис. 19, то есть плоскость (x, y)]. Таким образом, лучевые петли возникают не только в окрестности каустического острия, как в предыдущем случае, но и при полном отражении лучей от ионосферы в окрестности

Электронная концентрация

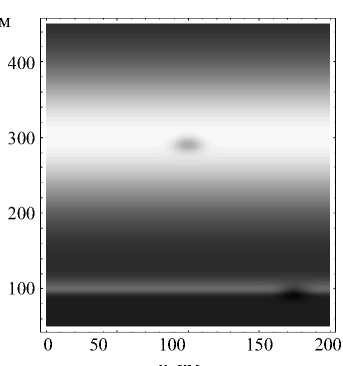
x , км

Рис. 16

z , к

Необыкновенная волна: 13,0 мГц; в = 0,4; у = 45 град

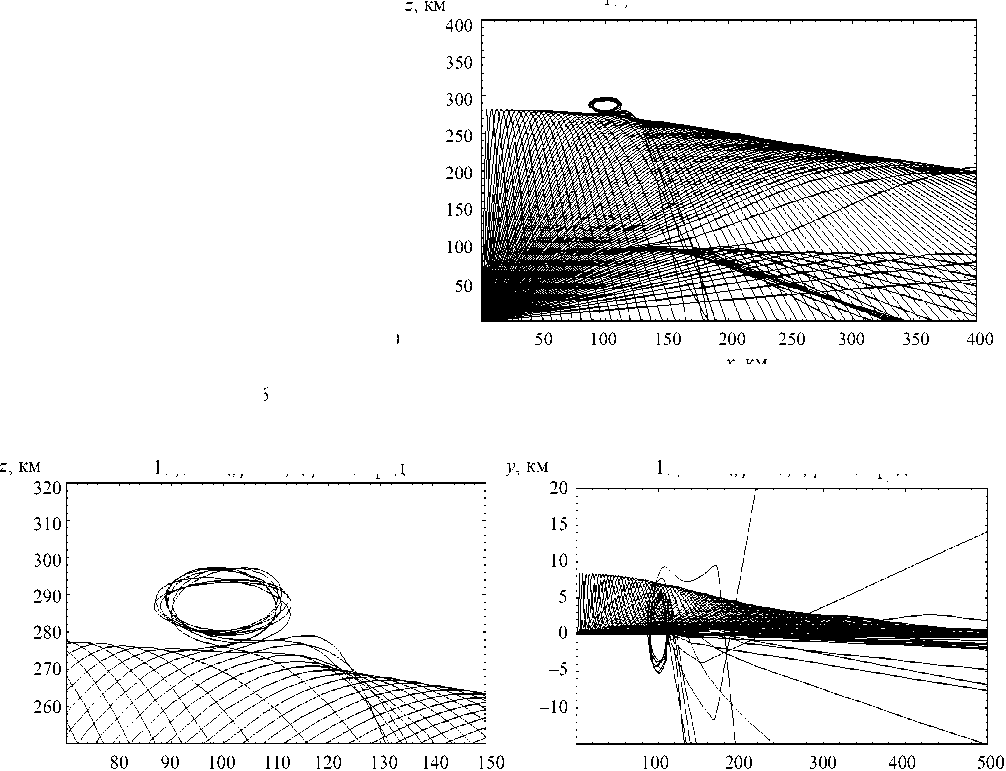
Необыкновенная волна: 13,0 мГц; в = 0,4; y = 45 град x, км x, км

Рис. 18

x , км

Рис. 17

Необыкновенная волна: 13,0 мГц; в = 0,4; Y = 45 град

гладкой каустики. Отсюда можно сделать вывод, что ионосферный аттрактор – устойчивое образование при наличии локальных неоднородностей.

Локальная неоднородность, расположенная в окрестности слоя Е , приводит к небольшому изменению каустической структуры, создаваемой этим слоем (рис. 17).

Рассмотрим теперь случай, когда область повышенной электронной концентрации лежит вне слоя (рис. 20): x_loc = z_loc = 100 км, y_loc = 0, β_loc = 0,3. Тогда неоднородность выталкивает лучи из области распространения, и на Земле возникают области с пониженной напряженностью электромагнитного поля (см. рис. 21). В данном примере длина этой зоны – более 200 км.

Вместо обычного каустического острия возникает структура, соответствующая особенности типа «ласточкин хвост» – А4.

Рис. 22 иллюстрирует выход луча из плоскости распространения в этом случае. Следует осо-

Рис. 19

бо отметить точки возврата лучевых траекторий в плоскости ( y , z ), хорошо видные на рисунке и характерные для лучей, отразившихся от слоя. На рис. 23 представлена лучевая структура в плоскости ( x , y ). Видна сложная каустическая структура лучей, отразившихся от ионосферы, с образованием волновой каспоидной катастрофы «ласточкин хвост». Эти лучи сначала смещаются в боковую плоскость, а затем частично возвращаются. Лучи, прошедшие ионосферу, смещаются в боковой плоскости на величину, определяемую углом выхода луча. Чем направление луча ближе к вертикальному, тем смещение меньше. Выйдя из ионосферы, лучи движутся параллельно.

Рассмотрим теперь случай, когда величина максимума ионосферного слоя периодически меняется (11).

n x

N f + P N e ) 1 + A sm — I , I        ( 2 x JJ

в , = - 0,3, x , = 80 км.

Электронная концентрация

Необыкновенная волна:

13,5 мГц; в = 0; у = 45 град z, км z, км

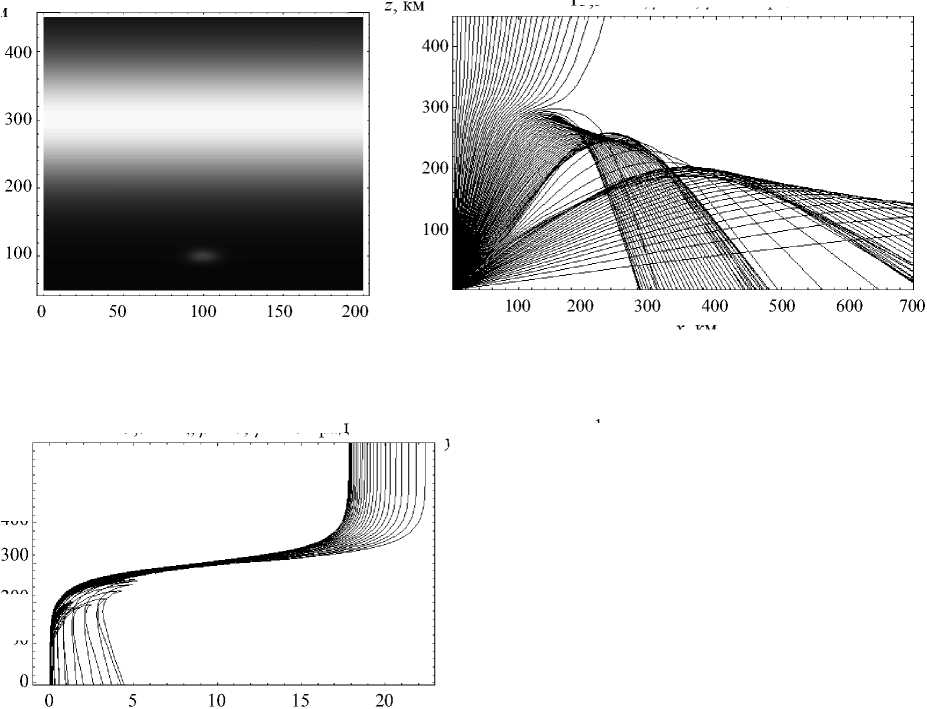
x , км

Рис. 21

Необыкновенная волна:

y , км

x , км

Рис. 20

Необыкновенная волна: 13,5 мГц; в = 0; Y = 45 град

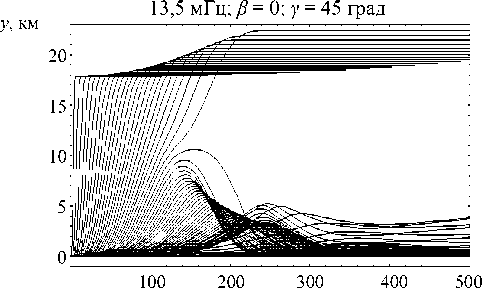
x , км

Рис. 23

центрации над источником необыкновенная волна, проходя ионосферный слой, фокусируется. В этом случае имеет место инверсия лучевой структуры. В проекции на плоскость ( y , z ) (см. рис. 26) все лучи расщепляются.

Рис. 22

На рис. 24 показано модельное распределение электронной концентрации справа и над источником излучения с рабочей частотой 13,5 МГц. Из результатов моделирования видно (рис. 25), что за счет понижения максимума электронной кон-

Электронная концентрация z, км

Необыкновенная волна: 13,5 мГц; в = 0; у = 45 град z, км

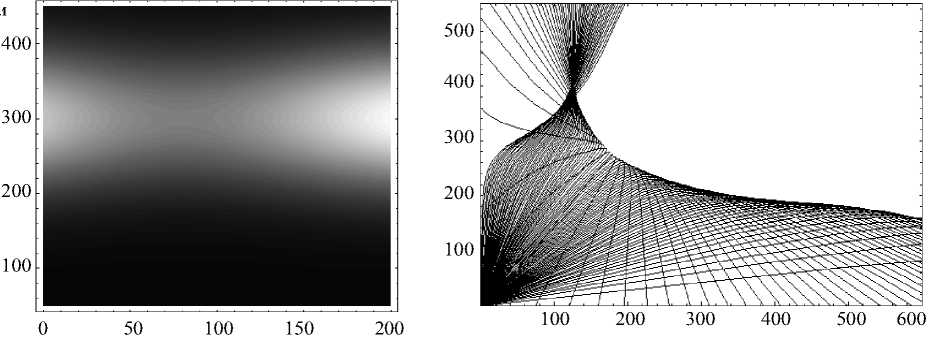
x , км

Рис. 25

x , км

Рис. 24

z , км

Необыкновенная волна:

13,5 мГц; в = 0; Y = 45 град

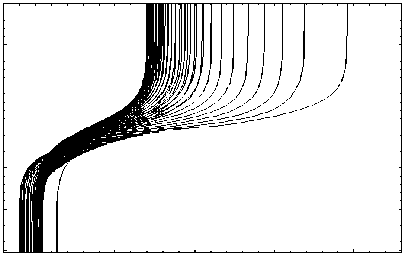
10       15

y , км

Рис. 26

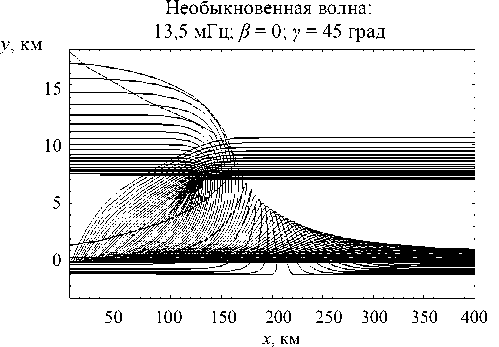
Рис. 27

Резко изменяется и структура лучей в плоскости ( x , y ). В результате инверсии при выходе из области фокусировки часть лучей отправляется налево, а часть – направо.

Как и в работах [1–4], рассмотрим модифи- кацию лучевой структуры «паук Д.С. Лукина» в присутствии локальной неоднородности. Начальное лучевое семейство образовано лучами, выходящими из источника в разные стороны почти вертикально (η = 88°).

z , км

z , км

Обыкновенная волна:

12,8 мГц; y = 12 град; п = 88 град

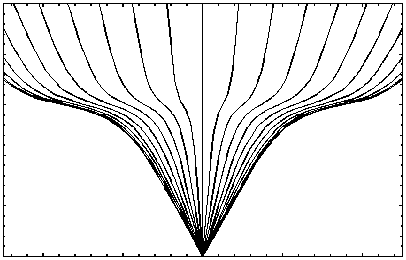
Рис. 28

-20      -10       0       10

x , км

Обыкновенная волна:

12,8 мГц; y = 12 град; п = 88 град

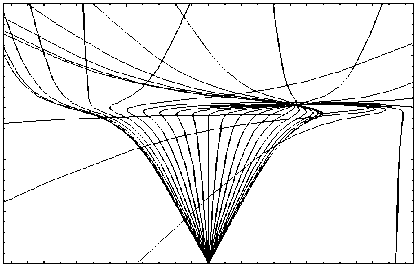
Рис. 29

-20      -10        0

x , км

z , км

Обыкновенная волна: 12,8 мГц; y = 12 град; П = 88 град

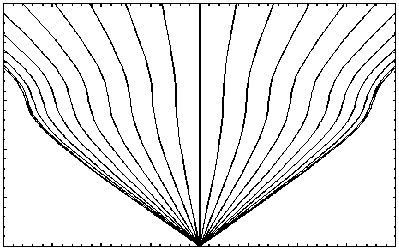
Рис. 30

-7,5   -5 -2,5   0    2,5    5    7,5    10

y , км

z , км

Обыкновенная волна:

12,8 мГц; y = 12 град; П = 88 град

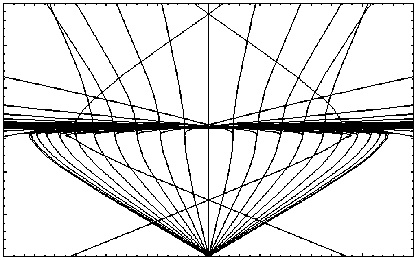
Рис. 31

-7,5   -5   -2,5    0    2,5     5    7,5    10

y , км

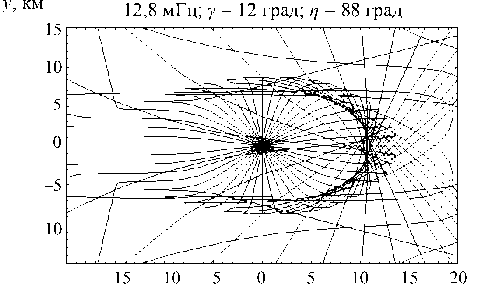
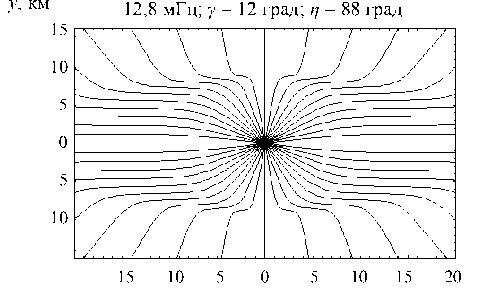
На рис. 28, 30, 32 приведены лучевые структуры в плоскостях ( x , z ), ( y , z ) и ( x , y ) в случае отсутствия локальной неоднородности. Рис. 32 соответствует структуре «паук Д.С. Лукина». Из рисунка видно, что лучи, вышедшие параллельно оси y , не отклоняются. Остальные лучи отклоняются, испытывая характерный изгиб.

На рис. 29, 31, 33 приведены результаты моделирования лучевых структур в плоскостях (x, z), (y, z) и (x, y) при наличии локальной неоднород- ности, центр которой расположен в точке с координатами (10 км, 0 км, 300 км). Неоднородность, разрушая регулярную структуру, как бы стягивает лучи (рис. 29). В проекции на плоскость (y, z) наличие неоднородности приводит к появлению фокусировки лучей на высоте 300 км (рис.31), а в проекции на плоскость (x, y) возникает каустика с каустическим острием – структура, характерная для отражения лучей от вогнутой поверхности (рис. 33).

Обыкновенная волна:                               Обыкновенная волна:

• x , км                                                   x , км

Рис. 32                                                          Рис. 33

В настоящей работе рассмотрены особенности лучевого распространения обыкновенной и необыкновенной электромагнитных волн в анизотропной ионосферной плазме при наличии локальных неоднородностей. Обнаружены сложные каустические фокусировки типа катастроф кас-поидного типа. Рассмотрены случаи неоднородностей как увеличивающих, так и понижающих электронную концентрацию ионосферной плазмы. Исследованы модели со слоями F и Е , а также – случаи присутствия одновременно нескольких локальных неоднородностей. Выявлено устойчивое образование лучевых петель в ионосфере – ионосферный аттрактор. Исследована модификация лучевой структуры «паук Д.С. Лукина» в присутствии локальной неоднородности.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проекты №№ 09-07-00189, 10-02-01103).