Исследование влияния масштабного фактора на прочностные характеристики искусственных кож

Витебский государственный технологический университет

Высокие требования, предъявляемые к потребительским свойствам и качеству современных изделий обувной промышленности, определяют её конкурентоспособность на внутреннем рынке Республики Беларусь и за рубежом. От качества исходных материалов, применяемых для изготовления обуви, зависит качество готового изделия. Управление качеством продукции требует знания свойств, умения правильно измерять и объективно оценивать важнейшие показатели качества, а также достоверно прогнозировать количественные характеристики свойств продукции [1, 2]. Одним из наиболее значимых показателей качества материалов, определяющих их технологическую пригодность для изготовления изделий из кожи, является нагрузка при разрыве, характеризующая прочность материала. Методику оценивая разрывной нагрузки искусственных кож (ИК) регламентируют соответствующие стандарты (ГОСТ 17361-71), где ее определяют при определенной фиксированной зажимной длине и ширине. Однако, с изменением зажимной длины и ширины меняется и значение разрывной нагрузки. Данная зависимость получила название масштабного эффекта. Анализ литературных источников показал недостаточную изученность вопросов, связанных с влиянием масштабного фактора на физико-механические свойства ИК [3–5].

Целью проводимых исследований является оценка влияния масштабного фактора на прочностные характеристики ИК. Научная новизна проведенных исследований состоит в использовании метода имитационного моделирования испытаний, применение которого позволяет выявить общие закономерности влияния линейных размеров поверхностно-протяженных материалов на их прочностные характеристики.

Экспериментальные исследования и обсуждение результатов

Предполагается, что каждый k -й образец ИК можно представить как некоторую систему, состоящую из последовательно-параллельно соединенных участков разной длины l_ik , разной ширины a_jk и разрывной нагрузки P_ijk, где k – изменяется от 1 до z ( z – число образцов в испытуемой партии), i – от 1 до n ( n – число структурных элементов по длине образца), j – от 1 до m ( m – число структурных элементов по ширине образца).

Исходными данными для моделирования являются: вид и параметры закона распределения разрывной нагрузки для образцов, состоящих из одного участка, ра зр ывная нагрузка которого по длине постоянна P_p (1), C_p (1); вид и пар а метры закона распределения участков системы n и C_n, m и C_m ; число испытываемых образцов z , где: P _p (1) – среднее значение разрывной нагрузки для образцов, состоящих из одного участка; C_p (1) – коэффициент вариации по разрывной нагрузке для образцов, состоящих из одного участка; P _p ( n , m ) – значение разрывной нагрузки поверхностно-протяжённого образца, состоящего из n и m числа структурных элементов; C_p ( n ) C_p ( m )– коэффициенты вариаций количества структурных элементов по длине и ширине образца соответственно.

С помощью программы, реализованной в математической системе Maple 19, на начальном этапе осуществлялось моделирование эксперимента по испытанию на разрыв из z образцов, состоящих из некоторого числа n структурных элементов по длине образца, при этом число структурных элементов по ширине образца приним а лось равным m = 1 с заданными значениями P_p (1) и C_p (1).

На втором этапе моделирования, полученные значения разрывной нагрузки Pij для некото- рого числа n структурных элементов, являлись исходными данными для моделирования эксперимента по испытанию на разрыв из z образцов и задаваемого числа m структурных элементов.

Некоторые гистограммы распределений значений P_p ( n , m ) и функции плотности вероятностей значений P _p (1) и P_p ( n , m ) представлены на рисунке 1.

В результате имитационного моделирования установлено, что распределение разрывной нагрузки образца P_p ( n , m ) не сов п адает с задаваемым законом распределения P_p (1). Отмечается появление правой асимметрии закона распределения и сдвиг модального значения в сторону меньших значений.

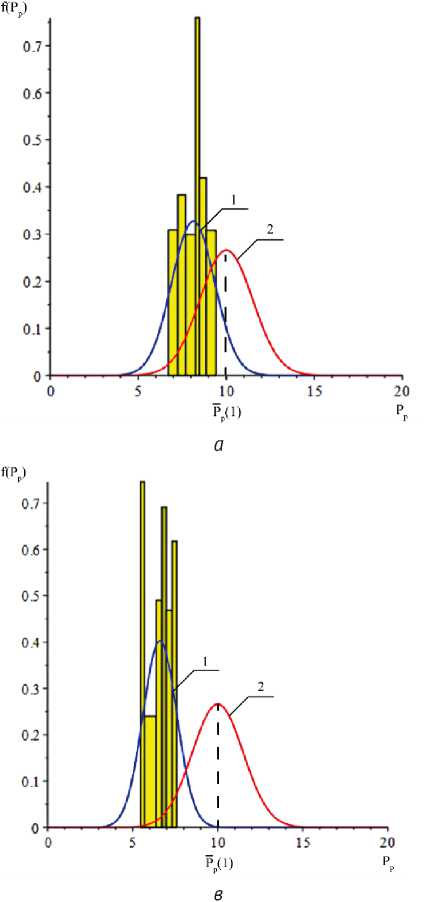
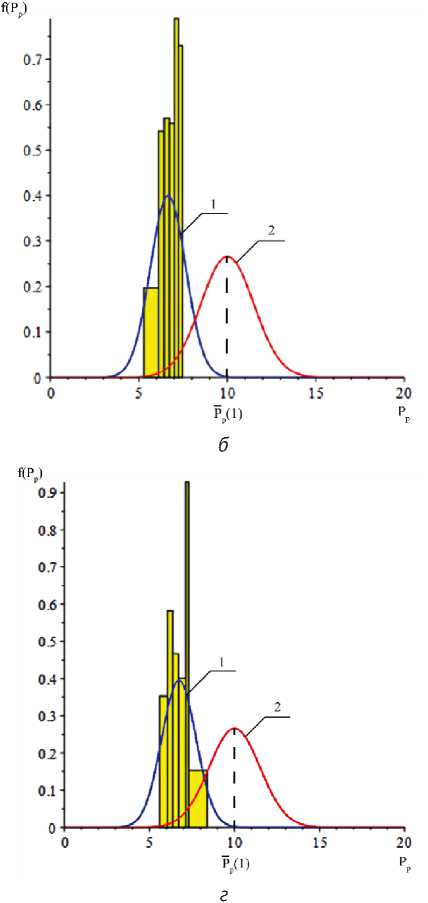
Рисунок 1 – Гистограммы рас п ределений значений P_p ( n , m ) и функции плотностей вероятностей значений P _p ( n , m ) (кривая 1) и P_p (1) (кривая 2) при а – n = 5, m = 1; б – n = 30, m = 1; в – n = 30, m = 5; г – n = 30, m = 30

Для выявления влияния геометрических размеров образца на среднее значение его разрывной нагрузки проводилось моделирование таких же экспериментов для образцов ИК с переменной длиной и шириной, которые считались пропорциональны числу n и m участков цепи.

На рисунке 2 представлены зависимости среднего значения разрывной нагрузки от числа структурных элементов n по длине исследуемо- го образца материала при различных значениях количества структурных элементов m по ширине образца.

Анализ данных зависимостей позволяет отметить, что увеличение количества структурных элементов n приводит к закономерному сниж е нию среднего значения разрывной нагрузки P_p . Это объясняется тем, что при увеличении числа участков n увеличивается вероятность появле-

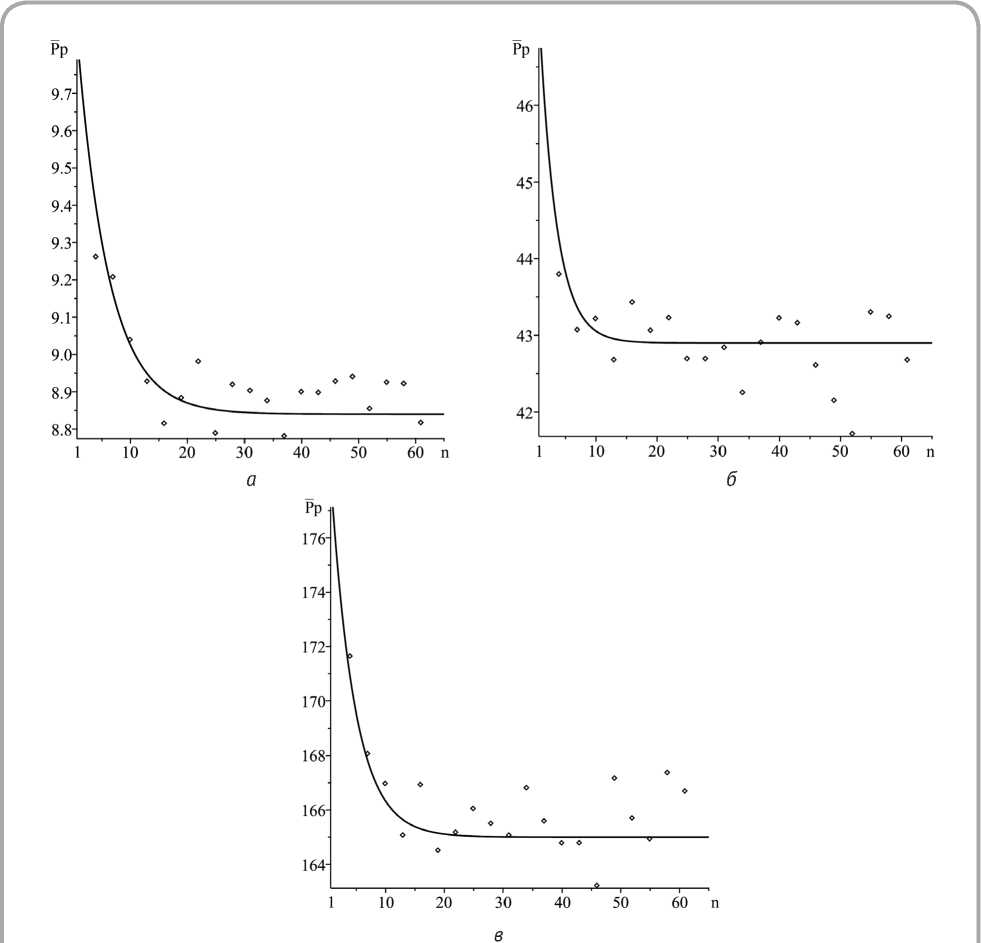
Рисунок 2 – Зависимости среднего значения разрывной нагрузки от числа структурных элементов по длине при различных значениях количества структурных элементов по ширине образца (а – m = 1;

б – m = 5; в – m = 20)

J

ния элемента ИК с наименьшей по абсолютной величине разрывной нагрузкой.

Для математического описания результатов моделирования используем математическую модель следующего вида [6]:

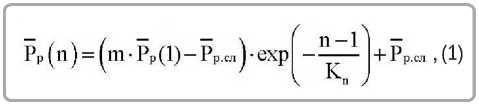
где P_p.сл – средняя разрывная нагрузка наиболее слабых звеньев, испытуемого образца материала; K_n – параметр модели, характеризующий темп умен ь шения среднего значения разрывной нагрузки P_p ( n ) при увеличении n (темповой параметр) [6].

Для количественной оценки степени проявления масштабного фактора прочности при увеличении ширины материала (предполагается, что ширина образца пропорциональна числу структурных элементов m ) введём следующий показатель Ψ , ( % ):

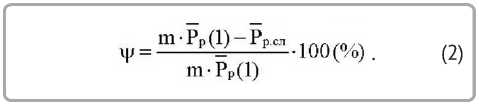
В результате имитационного моделирования получена зависимость введённого показателя от количества структурных элементов m , представленная на рисунке 3.

Анализ данной зависимости позволяет отметить закономерный характер снижения Ψ при увеличении количества структурных элементов m . При этом существует такое количество структурных элементов m , которое не влияет на относительное уменьшение разрывной нагрузки, вызванное действием масштабного фактора.

Так как зажимная длина L₀ пропорциональна n , зажимная ширина A₀ пропорциональна m , то по аналогии с (1) можно записать:

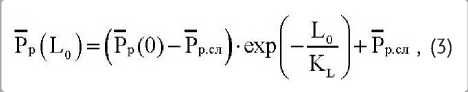
где P_p.сл – средняя разрывная нагрузка наибо ле е слабых звеньев, испытуемого образца ИК; P _p ( L₀ )– среднее значение разрывн о й нагрузки, как функции зажимной длины L₀ ; P_p ( 0 ) – среднее значение разрывной нагрузки образца, зажимная длина которого стремится к 0; K_L – имеет тот же смысл, что и Ê_n , то есть параметр модели

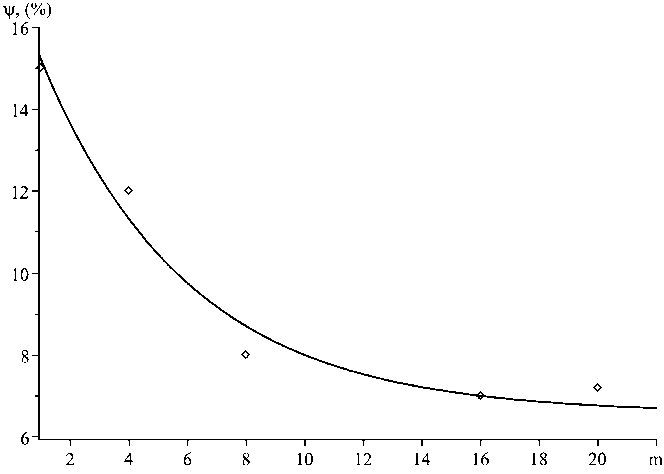
Рисунок 3 – Зависимость относительного уменьшения разрывной нагрузки от числа структурных

элементов m определяющий темп уменьшения разрывной нагрузки Pp(L0) при увеличении зажимной длины.

С целью экспериментальной проверки предварительных выводов, сформулированных выше, была произведена экспериментальная оценка разрывной нагрузки ИК при разных геометрических размерах. В качестве объекта исследования была выбрана двухслойная ИК, арт. Hongxin 11022-16. Толщина материала – 0,9 мм, поверхностная плотность - 435 г/м2. Испытания проводились с помощью универсальной испытательной машины TIME WDW-5 на пробах прямоугольной формы. При проведении экспериментальных исследований зажимная длина варьировалась в диапазоне от 50 до 300 мм с шагом 50 мм, а изменение ширины происходило в диапазоне от 20 до 60 мм с шагом 20 мм. Для каждой пробы различных размеров было проведено по 5 испытаний на разрыв в разных направления раскроя материала (вдоль и поперёк рулона). Некоторые результаты проведенных исследований представлены на рисунке 4.

Анализ данных зависимостей показывает закономерное снижение разрывной нагрузки с увеличением зажимной длины образца ИК. Параметры математической модели (3) представлены в таблице 1.

Анализ полученных в таблице 1 результатов показывает, что увеличение ширины образца прив о дит к закономерному увеличению значений Р_р ( 0 ) и P p сл , при этом темповой параметр KL остается практически постоянным.

ВЫВОДЫ

В результате проведенных исследований установлено, что практическое использование полученных результатов позволяет:

– осуществлять прогнозирование разрывной нагрузки Р_р образцов ИК при различных геометрических параметрах, что повышает информативность полуциклового испытания на растяжение;

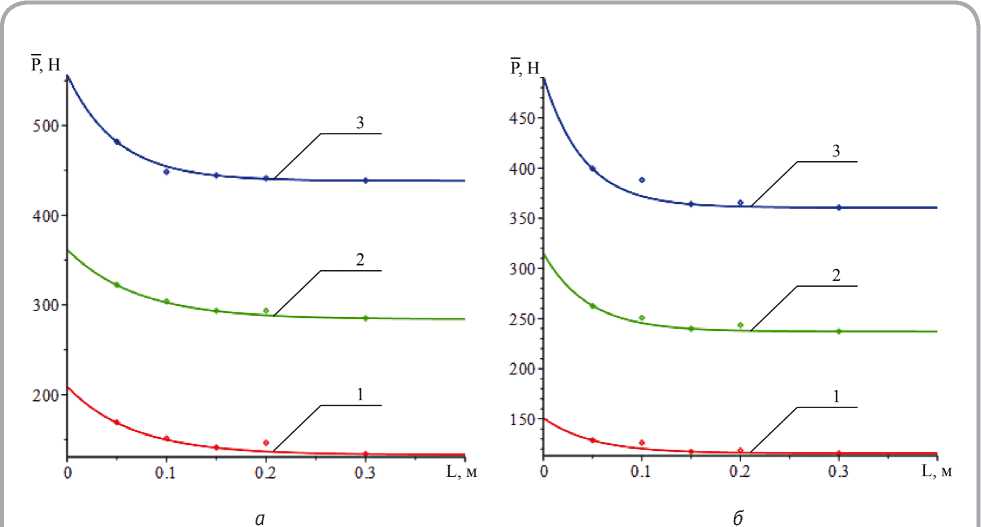
Рисунок 4 – Зависимости разрывной нагрузки от зажимной длины при разной ширине образца (1 - a = 0,02 м , 2 - a = 0,04 м , 3 - a = 0,06 м ; а - направление раскроя образца - вдоль, б - направления раскроя образца – поперек)

Таблица 1 – Параметры математической модели для исследуемого образца ИК при разных зажимных расстояниях и ширинах

«

Ширина образца, ìì	Pp.сл, H	Pp ( 0 ) , H	K L , ì-1	R2	Ψ Ä , %
	Направление раскроя – вдоль
20	132,9	209,0	0,076	0,96	57,3
40	284,0	361,8	0,073	0,99	27,4
60	438,4	556,7	0,056	0,99	27,0
	Направления раскроя – поперек
20	115,6	151,0	0,051	0,97	31,0
40	237,1	315,1	0,054	0,99	33,0
L 60	360,6	490,6	0,047	0,98	36,0 ____j

– предложить методологический подход к обоснованию геометрических размеров образцов ИК при ее испытаниях.

Таким образом, доказана возможность практического использования метода имитационного моделирования испытаний для изучения влияния масштабного фактора на прочностные характеристики искусственной кожи.