Исследование влияния нестабильности работы передающего лазерного канала, ошибок наведения, турбулентности атмосферы на характеристики его излучения в дальней зоне

Цитирование: Калинин В. С. Исследование влияния нестабильности работы передающего лазерного канала, ошибок наведения, турбулентности атмосферы на характеристики его излучения в дальней зоне / В. С. Калинин, А. А. Козирацкий, Д. В. Прохоров // Журн. Сиб. федер. ун-та. Техника и технологии, 2023, 16(7). С. 884–898. EDN: UJLYOS случайные неоднородности атмосферы [1]. Так, наличие турбулентной среды на трассе распространения значительно затрудняет возможность достижения заданного уровня интенсивности излучения на входе апертуры формирующей оптики оптико-электронного средства (ОЭС). Это связано с тем, что распространение в турбулентной атмосфере лазерного излучения большой мощности сопровождается различными линейными (поглощение и рассеяние, случайные блуждания, размытие и искажения пучка) и нелинейными (тепловая дефокусировка, газовый пробой) эффектами [1]. Вследствие чего происходит увеличение радиуса поперечного сечения луча и его отклонение от центра формирующей апертуры ОЭС, а, следовательно, уменьшение интенсивности поля излучения в поперечном сечении луча [2, 3].

В работах [4–8] проведено исследование эффективности вхождения в связь систем телекоммуникации с воздушными объектами управления на основе оценки плотности распределения интенсивности излучения передающего канала на входе фотоприемника в условиях ошибок наведения лазерного луча. Однако при проведении указанных исследований не учитывалось влияние турбулентной среды, приводящей к расширению лазерного луча и отклонению его от центра апертуры (центра наведения) в плоскости приема, оказывающей существенное влияние на качество приема сигнала, а также тепловой дефокусировки и эффекта газового пробоя. Поэтому целью настоящей работы является исследование влияния нестабильности работы передающего лазерного канала, ошибок наведения, турбулентности атмосферы на характеристики его излучения в дальней зоне.

Для достижения поставленной цели необходимо решить следующие задачи:

• а)    провести оценку распределения интенсивности лазерного излучения по поперечному сечению луча в случайно-неоднородной (турбулентной) среде;

• б)    на основе полученного аналитического выражения оценить плотность распределения интенсивности флуктуирующего излучения, создаваемого передающим лазерным каналом в дальней зоне;

• в)    провести оценку возможности превышения заданного уровня интенсивности излучения передающего лазерного канала на входе апертуры формирующей оптики оптико-электронного средства в условиях ошибок наведения и влияния турбулентной среды.

Оценка распределения интенсивности лазерного излучения в турбулентной среде

На рис. 1 представлена геометрия задачи распространения лазерного излучения в турбулентной атмосфере от источника, работающего в режиме плоской волны, расположенного в плоскости z = 0, до плоскости наблюдения z = L .

Пусть распределение комплексной амплитуды поля одномодового лазерного излучения на выходе передающего канала (в плоскости z = 0) изменяется по закону Гаусса [9–12]

Е = Е^- ', (1) где E ₀ – амплитуда поля на оси луча; Р - ^х² + у – расстояние от оси z до рассматриваемой точки; a 0 – эффективный (начальный) радиус луча (пучка) на выходе передающего канала; F – расстояние от плоскости z = 0 до центра излучения (для коллимированного пучка F ^-1 = 0); k = 2 π / λ – волновое число, λ – длина волны лазерного излучения.

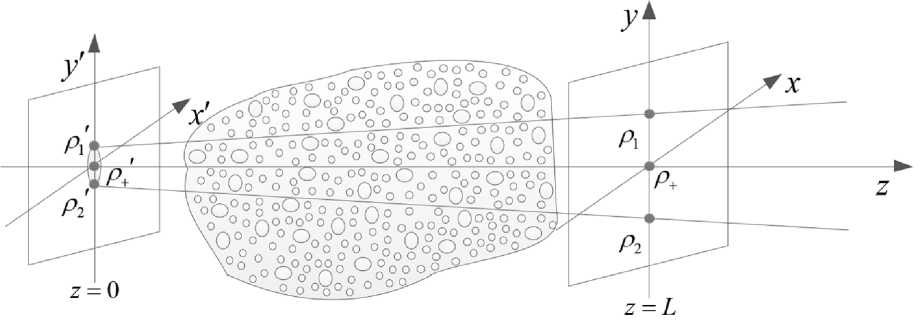
Рис. 1. Геометрия задачи распространения лазерного излучения в турбулентной атмосфере

Fig. 1. Geometry of the problem of laser radiation propagation in a turbulent atmosphere

Информацию о влиянии случайных неоднородностей диэлектрической проницаемости среды распространения на энергетические и когерентные свойства лазерного излучения в турбулентной атмосфере содержит функция взаимной когерентности поля Г 2 ( ρ , ρ + , z ). В общем случае при произвольных граничных условиях, если ввести на плоскости z = L координату ρ ₊ центра тяжести точек наблюдения ρ ₊ = ( ρ ₁ + ρ ₂)/2 и относительную координату ρ = ρ ₁ – ρ ₂ (рис. 1), функция взаимной когерентности поля имеет вид [2]:

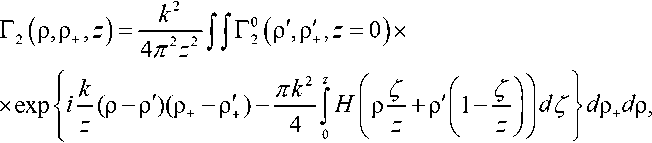
где r₂(p',p;,z = 0)– функция когерентности поля в плоскости z = 0; H (ρ) – структурная функция флуктуаций.

Используя условие (1), функцию когерентности поля в плоскости z = 0 определим выражением:

Г°(р',р;) = |£0|2 exp

p: p'2 i;.w

Q^ 4i7q F

Функция взаимной когерентности содержит информацию о распределении средней интенсивности в поперечном сечении луча и угловой структуре рассеянного излучения. Средняя интенсивность Др₊^) для случая, когда функция H^ = pC;p , что соответствует турбулентным флуктуациям диэлектрической проницаемости, с учетом затухания лазерного излучения в атмосфере на расстоянии L может быть получена на основании (2) и (3), положив ρ = 0, поэтому имеем

Kp^=lvi0^

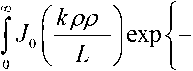
g4^_p._37rp_cyLp5A_pdp , (4)

где I 0 = | E 0 –² – плотность потока мощности в центре лазерного луча на выходе передающего канала; Г_а = e^a^^L – коэффициент затухания лазерного излучения в атмосфере, α _Σ = α_p + α_n – коэффициент суммарного ослабления потока излучения в среде за счет рассеяния и поглощения;

J 0 ( x ) – функция Бесселя нулевого порядка; gtL^^ + ea^VL + VF^ ; C"_E – структурная характеристика диэлектрической проницаемости; p – числовая константа [2].

Если ввести безразмерную переменную интегрирования t = (g(L)p/2a₀) , то (4) можно записать в виде:

I(p+,z = L) = I(

kVnT

g(L)42

Lg^

exp< -t - ^^-C"k²L

2^0 g(L)

t5'6 >dt.

Из выражения (5) следует, что интенсивность на оси пучка монотонно убывает с уве- личением расстояния, проходимого в турбулентной среде, а его радиус возрастает. Кроме этого, как показано в [2], случайные отклонения интенсивности от средней, имеющие различные знаки, всегда взаимно компенсируются, так что флуктуации диэлектрической проницаемости приводят лишь к перераспределению средней интенсивности в плоскости z = L = const.

На оси гауссова пучка средняя интенсивность может быть представлена в виде:

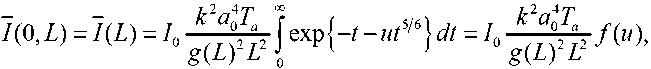
где _г1=^ЕР-С;кЧ где

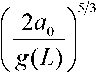
На рис. 2 представлены графики функции f ( u ), построенные в соответствии с выражением (6).

Из приведенного графика видно, что при больших значениях параметра u (при увеличении расстояния, проходимого в турбулентной среде L ) средняя интенсивность на оси гауссова

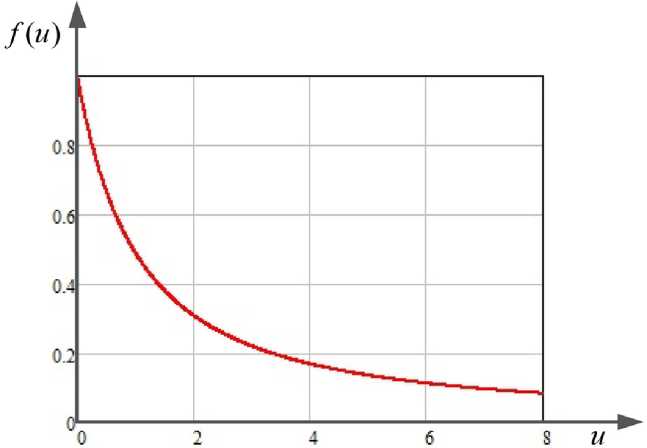
Рис. 2. График функции f ( u )

Fig. 2. Function Graph f ( u )

пучка монотонно убывает. При параметре u = 0 средняя интенсивность на оси гауссова пучка максимальна и соответствует средней интенсивности в однородной среде

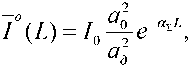
- L§W- —          R О где          – радиус луча в однородной среде.

В работах [2, 13] показано и экспериментально подтверждено, что для средней интенсивности расширение сфокусированного гауссова пучка на однородных приземных трассах в турбулентной атмосфере хорошо согласуется с расчетом по формуле:

Щ1

Тщ

^=/(»х dv

где S_d = 7ГС1"_д – площадь

луча в однородной среде после прохождения трассы длиной L ;

S^ — ЛGy – суммарная площадь уширенного луча, α Σ – радиус луча, уширенного (размытого)

турбулентностью.

Откуда радиус луча, уширенного (размытого) турбулентностью αΣ, можно определить вы- ражением:

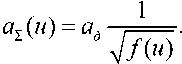
На рис. 3 представлен график зависимости радиуса луча, уширенного (размытого) турбулентностью от параметра u , построенной согласно (9) при α_д = 0,025 м.

Из графика зависимости видно, что с увеличением параметра u радиус луча, уширенного (размытого) турбулентностью, увеличивается, что при фиксированной дальности L = const объясняется повышением уровня турбулентности.

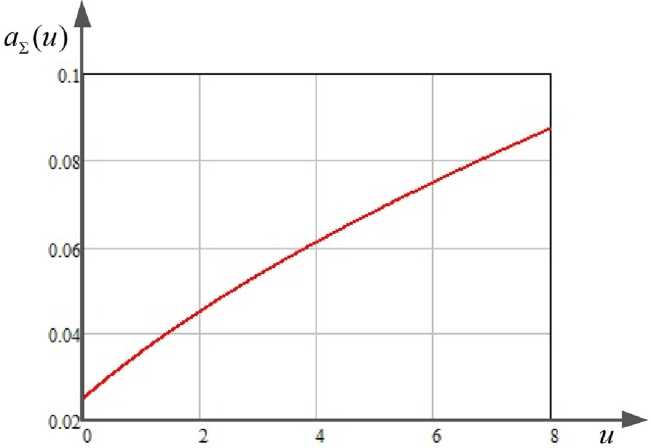
Рис. 3. График зависимости радиуса луча, уширенного (размытого) турбулентностью от параметра u

Fig. 3. Graph of the dependence of the beam radius broadened (blurred) by turbulence on the parameter u

Таким образом, на основе методов теории распространения электромагнитных волн оптического диапазона и математической статистики проведена оценка распределения средней интенсивности по поперечному сечению пучка лазерного излучения в случайно-неоднородной (турбулентной) среде, учитывающей линейные поглощение и рассеяние излучения молекулами и аэрозолями, а также случайное увеличение (размытие) радиуса луча вследствие турбулентности атмосферы.

Оценка плотности распределения интенсивности излучения, создаваемой передающим лазерным каналом в дальней зоне

Пусть лазер передающего канала работает в режиме значительно выше порогового ( ξ >> 0). В этом случае, как показано в [4, 14], плотность распределения интенсивности при генерации лазера, сопровождающаяся флуктуациями, имеет форму гауссовой плотности со средним значением ^1_ПГ [15]:

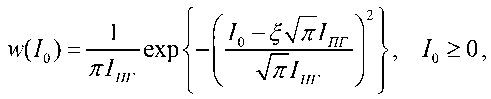
где IПГ – средняя пороговая интенсивность генерации лазера; ξ – параметр, изменяющийся в зависимости от режима работы лазера, зависящий от значений средней пороговой интенсивности генерации лазера.

Плотность распределения интенсивности лазерного излучения в плоскости наблюдения w(I) определим на основе выражения (6) с использованием метода функционального преобразования случайных величин [14]:

w(T) = —-—  e"J —-— exp < л1пг ao №

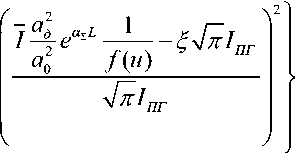
На рис. 4 представлены графики зависимости распределения интенсивности лазерного излучения W^I^ от нормированной величины q I / I_nr при различных значениях параметра u , построенные с использованием выражения (11). Характеристики передающего канала и типовые условия распространения лазерного излучения приведены в табл. 1.

Результаты анализа графиков, представленных на рис. 4, позволяют сделать вывод о том, что изменение формы закона распределения существенным образом определяется параметром u , характеризующим расходимость лазерного луча, уширенного (размытого) турбу-

Таблица 1. Характеристики передающего канала и условия распространения лазерного излучения

Table 1. Characteristics of the transmission medium and conditions for the propagation of laser radiation

Характеристика, единица измерения	IПГ , Вт / м 2	D , м	α 0 ≈ D /4, м	αp , рад	1 T ad=-«pL , м	ξ	L , м	α Σ , м
Значение	300	0,1	0,025	10–4	0,5	10	104	10–5

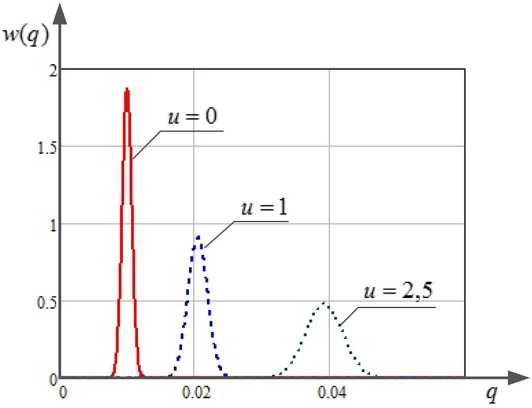
Рис. 4. Распределение интенсивности лазерного излучения w ( q ) от нормированной величины Ч ^ l^nr при различных значениях параметра u

Fig. 4. Distribution of the intensity of laser radiation from w(q) the normalized value Ч   I^пг for for various values of the parameter u лентностью в дальней зоне. При повышении уровня турбулентности (увеличении параметра u) дисперсия и среднее значение (математическое ожидание) величины q - I j I пг увеличиваются.

Таким образом, на основе использования метода функционального преобразования случайных величин проведена оценка плотности распределения интенсивности флуктуирующего излучения передающего лазерного канала в случайно-неоднородной (турбулентной) среде, создаваемой в дальней зоне.

Оценка возможности превышения заданного уровня интенсивности излучения передающего лазерного канала на входе апертуры формирующей оптики оптико-электронного средства в условиях ошибок наведения и влияния турбулентной среды

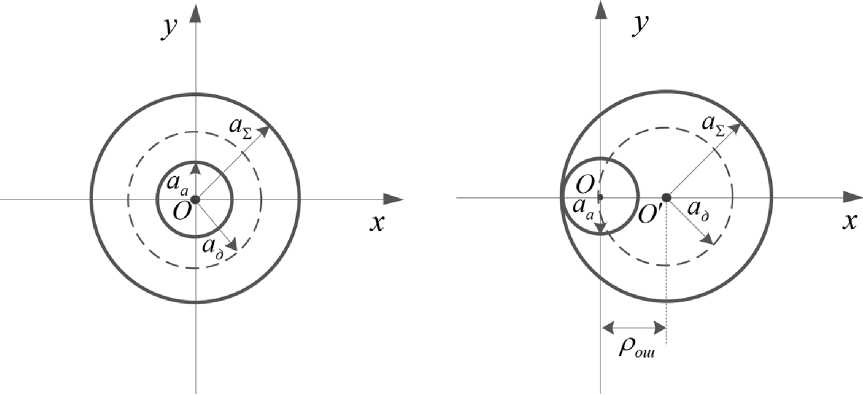
На рис. 5 показано поперечное сечение луча в плоскости оптико-электронного средства формирующей апертуры радиусом a_a в случае прохождения лазерного излучения через случайно-неоднородную (турбулентную) и однородную среду, радиусы которых составят a Σ и a д соответственно. На рис. 5а центр координатной оси (точка O ) совпадает с центром лазерного луча и формирующей оптики, он соответствует уширению (размытию) лазерного луча в результате прохождения через турбулентную среду (мелкомасштабная турбулентность). На рис. 5б точка O совпадает с центром формирующей оптики, точка O ′ с осью поперечного сечения луча, а ρ ош = a Σ – a a характеризует величину отклонения оси лазерного луча от центра апертуры в результате прохождения через турбулентную среду (крупномасштабная турбулентность), которая является случайной величиной.

а)                                                    б)

Рис. 5. Геометрия задачи: а) мелкомасштабная турбулентность; б) крупномасштабная турбулентность

Fig. 5. Problem geometry: a) small-scale turbulence; b) large-scale turbulence

Пусть ошибки отклонения оси лазерного луча от центра апертуры формирующей оптики распределены по закону Рэлея. Тогда вероятность наведения лазерного луча на апертуру формирующей оптики ОЭС с учетом (9) определим выражением:

^Рн = J ^ЛРошУРош ⁼¹“^{e 2<7}' ’ (12)

где σ l – линейная среднеквадратическая ошибка отклонения лазерного луча от центра формирующей апертуры фотоприемника. Для малоуглового приближения σ l ≈ σ α L , где ^ =(^J – угловое среднеквадратическое отклонение лазерного луча, – радиус когерентности поля плоской волны для однородной трассы, c^ – структурная характеристика флуктуаций показателя преломления среды.

Вероятность превышения порога заданного уровня интенсивностью излучения передающего лазерного канала на входе апертуры формирующей оптики ОЭС определим следующим выражением:

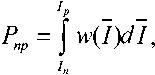
где I n – пороговая интенсивность; I p – пиковая интенсивность.

Нижний предел интегрирования в (13) определяется заданным пороговым значением интенсивности излучения, верхний предел – значением интенсивности, обеспечивающей купирование тепловой дефокусировки и эффекта газового пробоя. Последнее зависит от режима функционирования передающего лазерного канала (непрерывного или импульсного распространения).

Пиковую интенсивность с учетом линейных и нелинейных эффектов распространения, в предположении, что передающий канал фокусируется на расстоянии L без сканирования, – 892 – пренебрегая турбулентностью среды, для непрерывного режима распространения можно определить в следующем виде [1]:

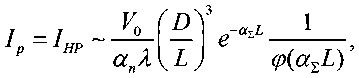
где V0 – скорость однородного поперечного ветра; λ – длина волны лазерного излучения; αn – коэффициент ослабления за счет поглощения; D – диаметр апертуры формирующей оптики передающего канала; <Р^ = "---^[^-l + ^Lj – корректирующий множитель, учиты вающий условие предельно малого ослабления, т.е. αΣL << 1.

Пиковую интенсивность в случае импульсного (многоимпульсного) распространения можно определить приблизительным соотношением [1]:

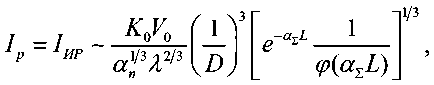
где K 0 – оптимальное число импульсов за время переноса V 0 / d .

Подставляя полученный закон распределения лазерного излучения в плоскости апертуры формирующей оптики ОЭС (11) в выражение (13), получим:

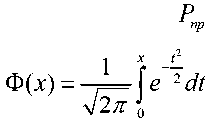
– интеграл вероятности.

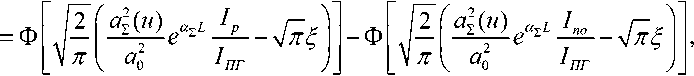
Считая, что события, состоящие в накрытии апертуры формирующей оптики ОЭС лазер- ным лучом и превышении порога заданного уровня интенсивностью излучения передающего лазерного канала, независимы, вероятность достижения заданного уровня интенсивности излучения в области ОЭС определим выражением:

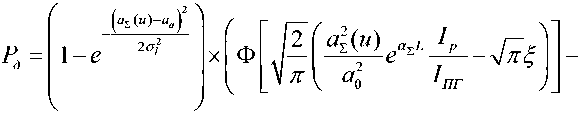
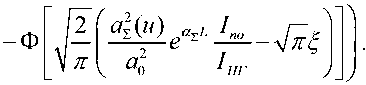
На рис. 6 представлены графики зависимости вероятности достижения заданного уровня интенсивности излучения от радиуса поперечного сечения луча в плоскости апертуры формирующей оптики ОЭС, уширенного (размытого) турбулентностью при различных значениях параметра u , определяемого структурной характеристикой флуктуаций диэлектрической проницаемости c^ на фиксированной дальности L . Графики построены в соответствии с выражением (17) для следующих исходных данных: a a = 0,05 м , a 0 = 0,025, I p = 500 Вт / м ², I no = 200 Вт / м ², I ПГ = 300 Вт / м ², ξ = 10, α Σ = 10^–5 1/ м , L = 5∙10³ м , σ l = 0,02 м .

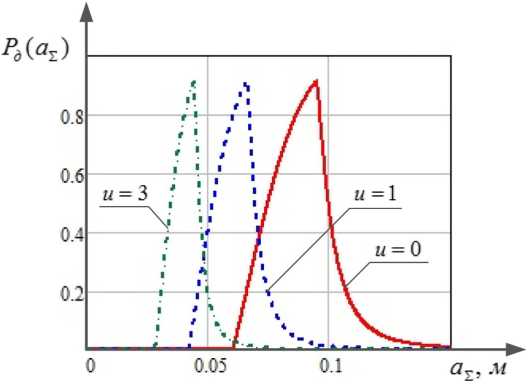
Рис. 6. Графики зависимостей вероятности достижения заданного уровня интенсивности излучения в плоскости ОЭС от радиуса поперечного сечения луча, уширенного турбулентностью при различных значениях параметра u

Fig. 6. Graphs of the dependences of the probability of reaching a given level of radiation intensity in the OES plane on the radius of the beam cross section, broadened by turbulence for various values of the parameter u

Результаты анализа графиков зависимостей, представленных на рис. 6, позволяют сделать следующие выводы:

• 1.    Существует оптимальное значение радиуса поперечного сечения луча в дальней зоне, обеспечивающее максимальное значение вероятности достижения заданного уровня интенсивности излучения в плоскости ОЭС.

• 2.    Сравнительный анализ полученных зависимостей, соответствующих прохождению лазерного излучения через однородную среду ( u = 0) и случайно-неоднородную среду с различным уровнем турбулентности ( u = 1, u = 3), показывает, что при увеличении параметра u оптимальное значение радиуса поперечного сечения луча уменьшается. Это объясняется тем, что при прохождении лазерного излучения через турбулентную атмосферу с высоким уровнем неоднородности интенсивность лазерного излучения уменьшается, что обуславливается уширением (размытием) лазерного луча, и для превышения заданного уровня интенсивности излучения передающего канала на входе апертуры формирующей оптики ОЭС заданного уровня ее становится недостаточно. Поэтому для повышения вероятности достижения заданного уровня интенсивности излучения необходимо уменьшать оптимальный угол расходимости лазерного излучения передающего канала.

На рис. 7 представлены графики зависимости вероятности достижения заданного уровня интенсивности излучения от радиуса поперечного сечения луча в плоскости апертуры формирующей оптики ОЭС, уширенного (размытого) турбулентностью, при различных значениях линейной среднеквадратической ошибки отклонения лазерного луча, возникающей при прохождении лазерного излучения через случайно-неоднородную среду (крупномасштабная турбулентность) и определяемой структурной характеристикой флуктуаций показателя преломления воздуха С^ на фиксированной дальности L . Зависимости построены для приведенных выше исходных данных при параметре u = 1.

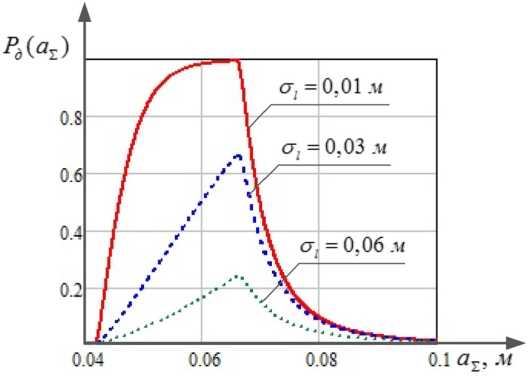
Рис. 7. Графики зависимости вероятности достижения заданного уровня интенсивности излучения от радиуса поперечного сечения луча, уширенного турбулентностью при различных значениях линейной среднеквадратической ошибки отклонения лазерного луча

• Fig. 7.    Graphs of the dependence of the probability of reaching a given level of radiation intensity on the radius of the cross-section of the beam, broadened by turbulence for various values of the linear root-mean-square error of the laser beam deflection

Снижение вероятности достижения заданного уровня интенсивности излучения при увеличении линейной среднеквадратической ошибки отклонения лазерного луча σ l обусловлено уменьшением интенсивности лазерного излучения на входе апертуры формирующей оптики ОЭС.

На рис. 8 представлены графики зависимости вероятности достижения заданного уровня интенсивности излучения от дальности при оптимальном значении угла расходимости излуче-

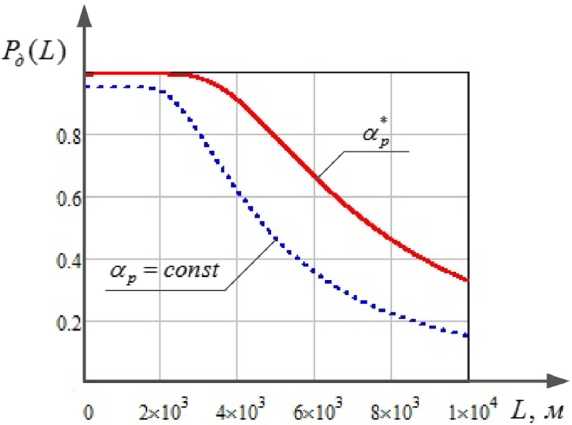
Рис. 8. Графики зависимости вероятности достижения заданного уровня интенсивности излучения от радиуса поперечного сечения луча, уширенного турбулентностью при различных значениях линейной среднеквадратической ошибки отклонения лазерного луча

• Fig. 8.    Graphs of the dependence of the probability of reaching a given level of radiation intensity on the radius of the cross-section of the beam, broadened by turbulence for various values of the linear root-mean-square error of the laser beam deflection

ния а_р = “р и при α_p = const и постоянных на протяжении трассы распространения значениях структурных характеристик флуктуаций показателя диэлектрической проницаемости и преломления среды.

Из графиков следует, что с увеличением длины трассы распространения вероятность достижения заданного уровня интенсивности излучения в плоскости ОЭС уменьшается, что обуславливается уменьшением интенсивности излучения в поперечном сечении луча за счет его расширения при прохождении через турбулентную атмосферу и ослабления в среде за счет рассеяния и поглощения. Однако существенным образом повысить вероятность достижения заданного уровня интенсивности излучения при прохождении лазерного излучения через турбулентную атмосферу позволяет формирование оптимального угла расходимости лазерного излучения передающего канала.

Заключение

Таким образом, проведено исследование влияния нестабильности работы передающего лазерного канала, ошибок наведения, турбулентности атмосферы на характеристики его излучения в дальней зоне. Исследование проведено на основе оценки плотности распределения интенсивности флуктуирующего излучения в плоскости апертуры формирующей оптики ОЭС при прохождении его через турбулентную атмосферу. Показано, что прохождение лазерного излучения через случайно-неоднородную среду сопровождается возникновением ошибок наведения лазерного луча и его расширением, оказывающими существенное влияние на возможность достижения заданного уровня интенсивности в плоскости ОЭС. Повышение вероятности достижения заданного уровня интенсивности излучения возможно за счет выбора оптимального угла расходимости лазерного излучения передающего канала, учитывающего флуктуации показателя диэлектрической проницаемости и преломления атмосферы.