Исследование влияния параметров амплитудных спиральных зонных пластинок на формируемый обратный поток энергии
Автор: Козлова Елена Сергеевна
Журнал: Компьютерная оптика @computer-optics
Рубрика: Короткие сообщения
Статья в выпуске: 6 т.43, 2019 года.
Бесплатный доступ
С помощью численного моделирования методом конечных разностей во временной области исследовано влияние параметров амплитудных спиральных зонных пластинок из серебра, золота, алюминия и хрома на продольную компоненту вектора Умова-Поинтинга в формируемых ими оптических вихрях. Показано, что алюминиевая спиральная зонная пластинка с высотой рельефа 50 нм даёт наименьшее значение продольной компоненты вектора Умова-Поинтинга на оптической оси. При этом спиральная зонная пластинка из золота является наименее эффективной для формирования вихревых пучков с обратным потоком энергии.
Оптические вихри, спиральная зонная пластинка, топологический заряд, круговая поляризация, обратный поток, вектор умова-поинтинга, fdtd-метод
Короткий адрес: https://sciup.org/140246536
IDR: 140246536 | DOI: 10.18287/2412-6179-2019-43-61093-1097
Текст научной статьи Исследование влияния параметров амплитудных спиральных зонных пластинок на формируемый обратный поток энергии
Оптические вихревые пучки принадлежат одному из таких типов сингулярностей, при котором фаза закручена в спираль [1–2]. Такие пучки имеют большое количество различных приложений, которые включают оптический захват микро- и наночастиц [3], оптические коммуникации [4], обработку материалов [5], а также обнаружение объектов [6]. В частности, для оптической манипуляции большой интерес представляют пучки с областью, где направление течения энергии обратно к направлению распространения пучка [7]. В таких пучках проекция вектора Умова–Поинтинга на оптическую ось является отрицательной [8].
Возможность формирования отрицательной продольной компоненты вектора Умова–Поинтинга была показана в ходе фокусировки пучков Бесселя, Эйри и других [9, 10]. Для формирования оптических вихрей отрицательной продольной компонентой вектора Умова–Поинтинга могут быть использованы специальные элементы, например, спиральные зонные пластинки (СЗП) [11] и металинзы на их основе [12]. Также было показано, что амплитудные СЗП могут формировать поля, аналогичные полям на выходе фазовых СЗП из кварцевого стекла [13].
В данной работе приведено исследование влияния параметров амплитудных СЗП с топологическим зарядом m =–2 на формирование продольной компоненты вектора Умова–Поинтинга. Были рассмотрены различные материалы для изготовления рельефа СЗП: серебро, золото, алюминий и хром. Для каждого варианта дополнительно оценивалось влияние толщины металлического слоя на формируемый обратный поток. Исследования проводились с помощью FDTD-метода с учётом частотной дисперсии ((FD)2TD-метода), реализованного в пакете FullWAVE.
Результаты моделирования
В работе рассматривались СЗП с топологическим зарядом m =–2, диаметром d =8 мкм и фокусным расстоянием f = 0,532 мкм. Элементы предполагаются быть изготовленными в тонких металлических плёнках на кварцевом стекле. Гауссов пучок с длиной волн 0,532 мкм, шириной перетяжки 3,5 мкм и правой круговой поляризацией рассматривался как падающее излучение. Все моделирования были выполнены с помощью (FD)2TD-метода, реализованного FullWAVE. Данный метод использует модель Селмейера для описания диэлектрической проницаемости кварцевого стекла и модель Друде–Лорентца – для металлов. Комплекснозначные показатели преломления для рассматриваемых материалов приведены в табл. 1.
|
Табл. 1. Коэффициенты преломления рассматриваемых |
|||
|
металлов длярельефа СЗП |
|||
|
Материал |
n |
||
|
Серебро |
0,133 + 3,025 i |
||
|
Алюминий |
0,887 + 6,257 i |
||
|
Золото |
0,579 + 2,183 i |
||
|
Хром |
2,769 + 4,185 i |
||
Вычисления проводились на следующих шагах дискретизации по пространству: 15 нм вдоль поперечных координат и 7 нм вдоль продольной. Временной шаг c Δ t был выбран равным 5 нм в соответствии с условием Куранта. Здесь и далее в ходе анализа результатов рассматривалось усреднённое по 10 периодам поле.
На рис. 1 показаны результаты моделирования. Вертикальные линии обозначают область теоретического фокуса СЗП ( z f = f + h , где h – высота рельефа).
Из рис. 1 видно, что область максимального обратного потока смещена ближе к границе элемента относительно области теоретического фокуса СЗП. При этом большему значению высоты рельефа соответствует большее значение интенсивности, в то время как зависимость продольной компоненты вектора Умова–Поинтинга от высоты рельефа является более сложной. Для более подробного анализа обратимся к табл. 2–5, в которых представлены результаты моде- лирования: минимальное Szmin и максимальное Szmax значение продольной компоненты Умова–Поинтинга и максимальная интенсивность Imax в плоскости наблюдения XY, которая расположена на расстоянии zнабл от элемента, где на оптической оси наиболее выражен обратный поток (т.е. имеется минимум продольной компоненты Sz).
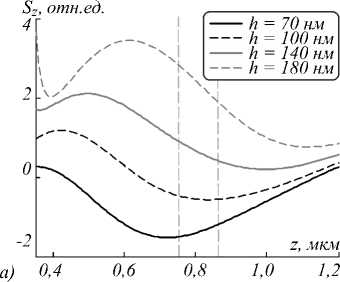
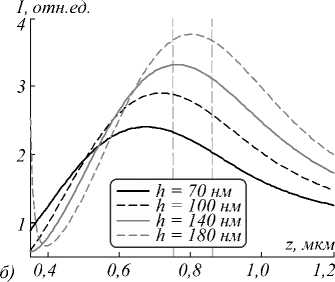
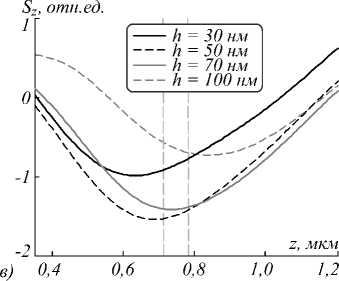
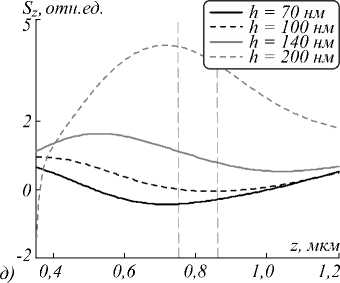
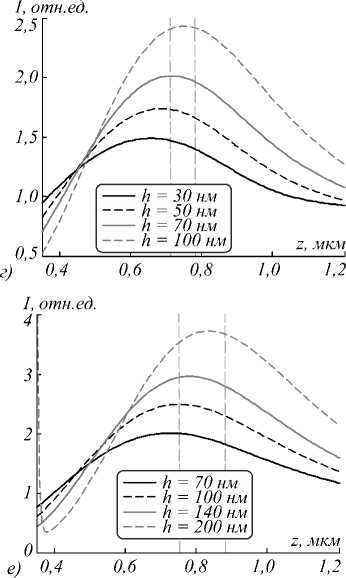
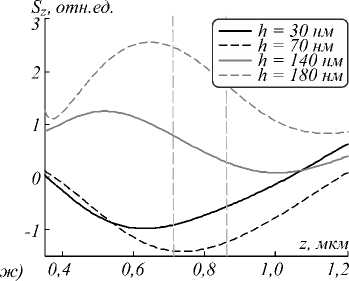
Рис. 1. Распределение продольной компоненты вектора Умова–Поинтинга (а, в, д, ж) и интенсивности (б, г, е, з) вдоль оптической оси в ходе формирования оптических вихрей СЗП из серебра (а, б), алюминия (в, г), золота (д, е) и хрома (ж, з)
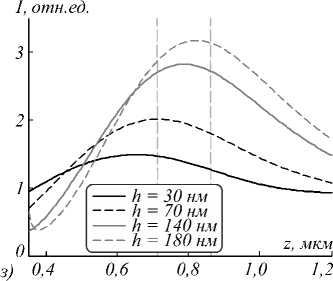
Табл. 2. Результаты моделирования для СЗП из серебра
|
h , нм |
Sz min , отн. ед. |
Sz max , отн. ед. |
I max , отн. ед. |
z набл , нм |
|
70 |
–1,52 |
3,62 |
6,58 |
501 |
|
100 |
–0,56 |
4,03 |
4,96 |
583 |
|
140 |
0,20 |
2,96 |
3,83 |
704 |
|
180 |
0,77 |
2,59 |
3,63 |
783 |
Табл. 3. Результаты моделирования для СЗП из алюминия
|
h , нм |
Sz min , отн. ед. |
Sz max , отн. ед. |
I max , отн. ед. |
z набл , нм |
|
30 |
–0,99 |
4,52 |
3,90 |
450 |
|
50 |
–1,54 |
6,89 |
5,47 |
486 |
|
70 |
–1,42 |
7,79 |
5,91 |
515 |
|
100 |
–0,73 |
7,74 |
5,44 |
590 |
Табл. 4. Результаты моделирования для СЗП из золота
|
h , нм |
Sz min , отн. ед. |
Sz max , отн. ед. |
I max , отн. ед. |
z набл , нм |
|
70 |
–0,44 |
2,92 |
3,33 |
494 |
|
100 |
–0,05 |
3,43 |
3,06 |
597 |
|
140 |
0,53 |
1,95 |
2,87 |
753 |
|
200 |
1,74 |
3,09 |
2,70 |
882 |
Табл. 5. Результаты моделирования для СЗП из хрома
|
h , нм |
Sz min , отн. ед. |
S z max , отн. ед. |
I max , отн. ед. |
z набл , нм |
|
30 |
–0,98 |
3,39 |
3,66 |
630 |
|
70 |
–1,42 |
3,61 |
4,47 |
735 |
|
140 |
0,07 |
2,44 |
3,26 |
1001 |
|
180 |
0,82 |
2,61 |
2,99 |
1141 |
В каждой таблице выделена строка, соответствующая оптимальной высоте рельефа СЗП, при которой величина обратного потока энергии и интенсивность поля максимальны. Из табл. 2–5 хорошо видно, что в большинстве случаев плоскость наблюдения находится ближе теоретического фокуса, кроме случая с СЗП из хрома, которая даёт минимум продольной компоненты Умова–Поинтинга на расстоянии 735 нм. При этом во всех рассматриваемых случаях оптимальная высота рельефа составляет порядка 50–70 нм.
Из табл. 4–5 и рис. 1 видно, что наиболее эффективными для генерации оптических вихрей с обратным потоком энергии на оптической оси являются СЗП в тонких плёнках алюминия и серебра. Отдельно стоит отметить случай с золотой плёнкой (рис. 1 д ), в котором обратный поток фактически отсутствует.
На рис. 2 показано поведение вектора Умова– Поинтинга в сформированном оптическом вихре.
Из рис. 2 видно, что в формируемом оптическом вихре присутствует обратный поток (рис. 2 а ) и спиральный поток (рис. 2 б ).
Заключение
В работе показано, что использование различных материалов для изготовления СЗП может существенно повлиять на формирование обратного потока энергии. Так, использование серебряных и алюминиевых плёнок толщиной порядка 50–70 нм позволяет получить наименьшее значение продольной компоненты вектора Умова–Поинтинга на оптической оси, в то время как использование золотой плёнки значительно уменьшает величину обратного потока вплоть до его полного исчезновения (рис. 1 д ). Данные СЗП планируется изготовить с помощью технологий электронно-лучевой литографии и исследовать экспериментально с помощью ближнепольного микроскопа.
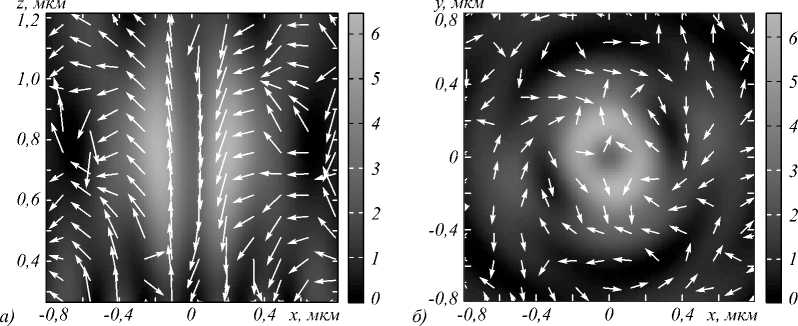
Рис. 2. Направление вектора Умова – Поинтинга, наложенное на интенсивность в плоскости XZ (а) и XY (б) для серебряной СЗП с высотой рельефа 70 нм
Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 18-0701380) и Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение №007-ГЗ/Ч3363/26).
Список литературы Исследование влияния параметров амплитудных спиральных зонных пластинок на формируемый обратный поток энергии
- Kitamura, K. Generation of optical vortex beam by surface-processed photonic-crystal surface-emitting lasers / K. Kitamura, M. Kitazawa, S. Noda // Optic Express. -2019. - Vol. 27, Issue 2. - P. 1045-1050. - DOI: 10.1364/OE.27.001045
- Padgett, M.J. Orbital angular momentum 25 years on / M.J. Padgett // Optic Express. - 2017. - Vol. 25, Issue 10. -P. 11265-11274. - DOI: 10.1364/OE.25.011265
- Yevick, A. Tractor beams for optical micromanipulation / A. Yevick, D.G. Grier // Proceedings of SPIE. - 2016. -Vol. 9764. - 97641A. - DOI: 10.1117/12.2212730
- Lavery, M.P.J. Free-space propagation of high-dimensional structured optical fields in an urban environment / M.P.J. Lavery, C. Peuntinger, K. Gunthner, P. Banzer, D. Elser, R.W. Boyd, M.J. Padgett, C. Marquardt, G. Leuchs // Science Advances. - 2017. - Vol. 3, Issue 10. - e1700552. - DOI: 10.1126/sciadv.1700552
- Takahashi, F. Picosecond optical vortex pulse illumination forms a monocrystalline silicon needle / F. Takahashi, K. Miyamoto, H. Hidai, K. Yamane, R. Morita, T. Omatsu // Scientific Reports. - 2016. - Vol. 6. - 21738. - DOI: 10.1038/srep21738
- Lan, C. Electrostatic field invisibility cloak / C. Lan, Y. Yang, Z. Geng, B. Li, J. Zhou // Scientific Reports. - 2015. - Vol. 5. - 16416. -
- DOI: 10.1038/srep16416
- Yuan, G. "Plasmonics" in free space: observation of giant wavevectors, vortices, and energy backflow in superoscilla-tory optical fields / G. Yuan, E.T.F. Rogers, N.I. Zheludev // Light: Science & Applications. - 2019. - Vol. 8, Issue 2. -P. 2047-7538. -
- DOI: 10.1038/s41377-018-0112-z
- Стафеев, С. С. Поведение продольной компонента: вектора Пойнтинга при острой фокусировке оптических вихрей с круговой поляризацией / С.С. Стафеев, А.Г. Налимов // Компьютерная оптика. - 2018. - Т. 42, № 2. - С. 190-196. -
- DOI: 10.18287/2412-6179-2018-42-2190-196
- Mitri, F.G. Superposition of nonparaxial vectorial com-plex-source spherically focused beams: Axial Poynting singularity and reverse propagation / F.G. Mitri // Physical Review A. - 2016. - Vol. 94, Issue 2. - 023801. -
- DOI: 10.1103/PhysRevA.94.023801
- Mitri, F.G. Reverse propagation and negative angular momentum density flux of an optical nondiffracting nonparaxi-al fractional Bessel vortex beam of progressive waves / F.G. Mitri // Journal of the Optical Society of America A. - 2016. - Vol. 33, Issue 9. - P. 1661-1667. -
- DOI: 10.1364/JOSAA.33.001661
- Liu, Y. Generation of perfect vortex and vector beams based on Pancharatnam-Berry phase elements / Y. Liu, Y. Ke, J. Zhou, Y. Liu, H. Luo, S. Wen, D. Fan // Scientific Reports. - 2017. - Vol. 7. - 44096. -
- DOI: 10.1038/srep44096
- Котляр, В.В. Сравнение величин обратного потока энергии в остром фокусе светового поля с поляризационной и фазовой сингулярностями / В.В. Котляр, А.Г. Налимов, С.С. Стафеев // Компьютерная оптика. -2019. - Т. 43, № 2. - С. 174-183. -
- DOI: 10.18287/24126179-2019-43-2-174-183
- Козлова, Е.С. Моделирование генерации оптических вихрей с помощью спиральной зонной пластинки из серебра / Е.С. Козлова // Компьютерная оптика. - 2018. -Т. 42, № 6. - С. 977-984. -
- DOI: 10.18287/2412-61792018-42-6-977-984


