Исследование влияния параметров расчетного трехмерного вязкого течения на прогнозные характеристики осевого насоса

В статье приведены результаты расчетного исследования проточных частей 2-х осевых насосов. Проточная часть первого осевого насоса с коэффициентом быстроходности n S ≈500, представленная на рис. 1, состояла из направляющего аппарата (НА), рабочего колеса (РК) и лопаточного выправляющего аппарата (ВА). Численные исследования проведены с использованием программного комплекса ANSYS CFX 12.

Первоначально была исследована сеточная независимость решения с целью определения минимального количества элементов обеспечивающего приемлемую точность решения. Упрощенная расчетная область включала один межлопастной канал направляющего аппарата, один канал рабочего колеса и один канал выправляющего аппарата. Для построения сеток использована программа ICEM CFD. С её помощью были построены 7 вариантов расчетных сеток. Сетки неструктурированные с

Свобода Дмитрий Геннадьевич, ассистент кафедры гидромашиностроения.         E-mail:        svo-

тетраэдральной формой элементов. Варианты сеток отличались друг от друга размером глобального максимального элемента и плотностью сеток вблизи кромок лопастей (таблица 1). По данным представленным в таблице 1, были построены зависимости интегральных параметров рабочего колеса (рис. 2) и выпрямляющего аппарата (рис. 3) от густоты расчетной сетки.

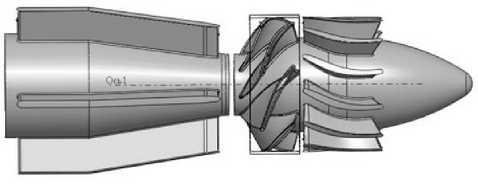
Рис. 1. Общий вид проточной части насоса с n S ≈500

Для построения сеток использована программа ICEM CFD. С её помощью были построены 7 вариантов расчетных сеток. Сетки неструктурированные с тетраэдральной формой элементов. Варианты сеток отличались друг от друга размером глобального максимального элемента и плотностью сеток вблизи кромок лопастей (таблица 1). По данным, представленным в таблице 1, были построены зависимости интегральных параметров рабочего колеса (рис. 2) и выпрямляющего аппарата (рис. 3) от густоты расчетной сетки.

Таблица 1. Расчетные данные

№	РК	ВА	Q	H РК	η РК	H Т	dh ВА	dη ВА	H	η
	тыс. эл.	тыс. эл.	м3/ч	м	%	м	м	%	м	%
1	187,9	147,7	2277	5,51	84,8	6,50	0,41	6,3	4,84	78,5
2	301,0	234,3	2277	5,44	85,4	6,37	0,37	5,8	4,78	79,6
3	391,3	304,1	2277	5,60	86,7	6,46	0,38	5,9	4,90	80,8
4	570,9	424,7	2277	5,93	88,1	6,73	0,38	5,6	5,20	82,5
5	892,3	670,8	2277	6,17	89,3	6,91	0,37	5,4	5,45	83,9
6	1539,4	1126,2	2277	6,30	90,2	6,98	0,36	5,2	5,62	85,0
7	3172,3	2314,3	2277	6,44	91,0	7,08	0,35	4,9	5,73	86,1

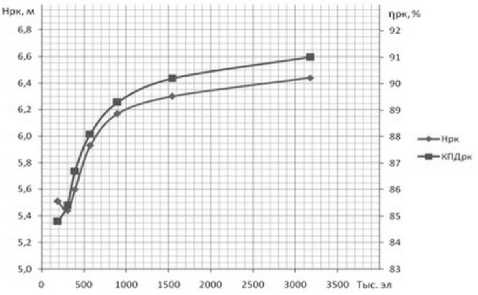
Рис. 2. Зависимость изменения напора и КПД РК от количества элементов расчетной сетки ( Q=Q опт )

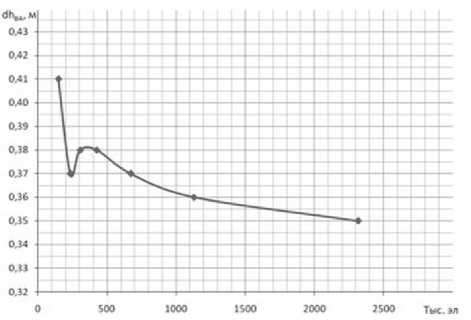
Рис. 3. Зависимость изменения потерь напора в проточной части ВА от количества элементов расчетной сетки ( Q=Q опт )

расчетная сетка с параметрами, соответствующими варианту № 7. Некоторое увеличение напора насоса и КПД связанное с дальнейшим возможным увеличением количества элементов расчетных сеток пойдет в запас. Из проведенных численных исследований можно сделать вывод, что характеристики рассматриваемого осевого насоса имеют большую зависимость решения от густоты расчетной сетки.

Для данного насоса также были выполнены исследования влияния расположения границы разделения – поверхности интерфейса (ПИ) между вращающимся рабочим колесом и неподвижной лопастной системой выпрямляющего аппарата в проточной части насоса на результаты расчёта интегральных параметров. Расчетная область включала в себя один межлопаточный канал НА, РК и ВА (рис. 4).

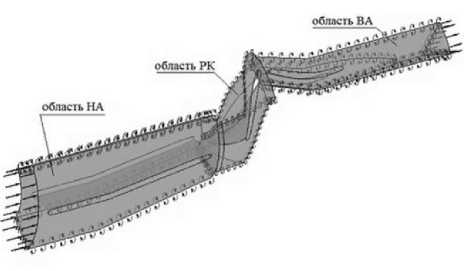
Рис. 4. Расчетная модель проточной части насоса с n S ≈500

Как видно из рис. 2 и 3, при увеличении количества элементов свыше 1500 тыс. изменение интегральных параметров осевого насоса происходит с меньшей интенсивностью. С улучшением качества сеток, как и следовало ожидать, значения результирующих невязок падают, что свидетельствует о лучшей сходимости расчета. Расчет на очень грубых сетках дает сходимость невязок только порядка 10-4, что является недостаточным. Окончательно для расчета характеристик насоса была принята

Если принять расстояние между лопастными системами РК и ВА за 100%, то, обычно поверхность интерфейса задается на расстоянии 50%. Были подготовлены геометрии сеток РК и ВА, в которых поверхность интерфейса задавалась на расстоянии 5% и 95%. При проведении исследований на поверхности интерфейса задавалось условие сопряжения – Stage Averaging. То есть, на поверхности интерфейса выполняется осреднение параметров расчета в окружном направлении, полагается, что следы от лопастей элемента проточной части РК полностью сглаживаются, и течение на входе в элемент проточной части ВА является осесимметричным.

Еще одной актуальной задачей исследования параметров расчетной модели, является задание выходной границы (ВГ) проточной части насоса. Были подготовлены геометрии сеток, сделаны расчеты и проведено сравнение интегральных параметров для двух вариантов проточной части. В варианте 1 выходная граница задавалась на расстоянии ~1,5 DРК. В варианте 2 выходная граница задавалась на расстоянии ~ 5 DРК. На рис. 5 показана расчетная модель насоса с границей выходной области расположенной на расстоянии 5 DРК. Расчетные исследования проводились с использованием программного комплекса ANSYS CFX 12 для оптимального режима работы насоса. В таблице 2 представлены значения интегральных параметров, полученные по результатам проведенных расчетов.

Выходная граница ночной части насоса

Рис. 5. Расчетная модель насоса с границей выходной области расположенной на расстоянии 5 D РК

Таблица 2. Расчет интегральных параметров

Расчетные интегральные параметры	ВГ=1,5D РК ; ПИ=50%	ВГ=5D РК ; ПИ=50%	ВГ=1,5D РК ; ПИ=5%	ВГ=1,5D РК ; ПИ=95%
напор РК, (м)	6,33	6,33	6,42	6,25
КПД РК (%)	90,37	90,35	90,57	89,8
потери в НА (м)	0,038	0,039	0,038	0,038
потери в ВА (м)	0,49	0,53	0,49	0,47
напор насоса (м)	5,55	5,58	5,55	5,31

Примечание: ВГ – выходная граница; ПИ – поверхность интерфейса

Промежуточные выводы:

• 1.    Присоединение дополнительных областей за ВА (увеличение расстояния до выходной границы с 1,5 D РК до 5 D РК ) не повлияло на величину напора, определяемую как разность полных энергий на выходе из ВА и входе в НА (или РК). Данное утверждение является справедливым при условии отсутствия циркуляционных потерь (остаточной закрутки за ВА).

• 2.    В осевых насосах, когда расстояние между лопастными системами соседних элементов проточной части достаточно велико, расположение границы разделения (поверхности интерфейса) между вращающимся рабочим колесом и неподвижной лопастной системой выпрямляющего аппарата в проточной части насоса мало влияет на результаты расчёта интегральных параметров. Присутствует незначительное уменьшение напора (~1,25%) и КПД (~0,6%) при смещении поверхности интерфейса вплотную к лопаткам ВА.

Методика расчета интегральных характеристик была апробирована на втором осевом насосе ОД-21 (Q=640 м3/час, H=1,63 м, n=1200 об/мин) с коэффициентом быстроходности nS=1300, для которого имелись экспериментальные характеристики, полученные на кафедре гидромашиностроения СПбГПУ. Расчетная модель насоса ОД-21 представлена на рис. 6. На входе в расчетную область задавалось полное давление, на выходе – массовый расход. Расчет течения проводился в стационарной постановке. Режим течения – турбулентный. Для замыкания уравнений Рейнольдса использовалась стандартная k - ε модель турбулентности. Интенсивность турбулентности на входе задавалась 5% (по умолчанию). Для поверхностей с условием “стенка” в расчетах использовались масштабируемые функции стенки.

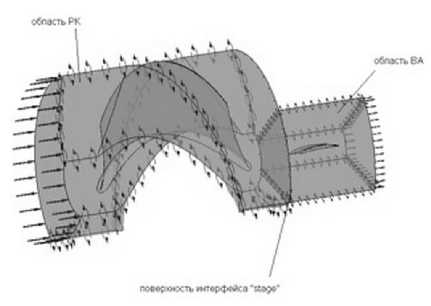
Рис. 6. Расчетная модель проточной части насоса ОД-21 ( n S =1280)

Расчетная сетка – неструктурированная, ячейки сетки в ядре потока представляли собой тетраэдры. Вблизи входных и выходных кромок рабочего колеса производилось сгущение элементов. Вблизи твердых стенок для описания пограничного слоя было создано 11 слоев призматических элементов. Полученное распределение безразмерного размера Y+ подтвердило правильность выбора параметров расчетной сетки (Y+<100 для высокорейнольд-совой модели с масштабируемыми функциями стенки).

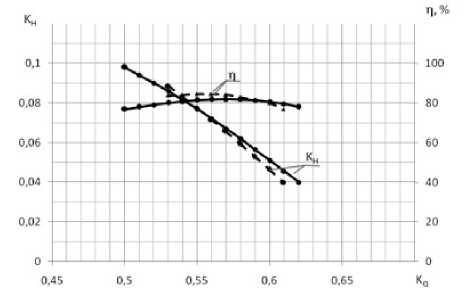
Рис. 7. Характеристики насоса ОД-21 в зависимости от режима работы: – физический эксперимент; ---- численный эксперимент

На рис. 7 приведено сопоставление напорных характеристик насоса и значений КПД, полученных по результатам физического и численного эксперимента. При этом значения гидравлического КПД были получены расчетом вязкого течения, а объемный и механический КПД в расчете не учитывались.

Из сравнения интегральных расчетных и экспериментальных параметров потока можно видеть, что расхождение по напору лежит в пределах до 10%, по КПД – до 2,5%. В целом, имеет место хорошее согласование интегральных параметров при численном и экспериментальном исследовании проточной части осевого насоса ОД–21. Следовательно, можно сделать вывод, что использованная методика может быть применена при расчете характеристик проточных частей осевых насосов.

RESEARCH THE INFLUENCE OF PARAMETERS OF RATEDTHREE-DIMENSIONAL VISCOUS FLOW ON THE PROGNOSTICCHARACTERISTICS OF THE AXIAL PUMP