Исследование влияния паразитных колебаний вибрационного преобразователя массового расхода на результаты измерений

Введение. В последние десятилетия положено начало широкому распространению кориолисовых массовых расходомеров. Выпуск фирмой Micro Motion Inc. и последующая успешная эксплуатация вибрационного преобразователя с двумя U -образными трубками показали такие высокие качества данного типа расходомеров, как простота конструкции, высокая точность и независимость показаний от физических свойств измеряемой среды. Однако некоторые недостатки двухтрубной конструкции, например, наличие разветвлений потока и высокая жесткость трубок, делали ее пригодной только для измерений расхода незагрязненных жидкостей, а измерения массового расхода газов, легких и неньютоновых жидкостей оставались за границами области ее применения.

Вибрационные преобразователи массового расхода с одной U -образной трубкой не имеют основного недостатка двухтрубных преобразователей – прогрессирующей погрешности измерения массового расхода из-за нарушений симметрии разветвленного потока в трубках вибрационного преобразователя. Недостатки, свойственные однотрубным преобразователям (ограниченная пропускная способность и пониженная чувствительность к расходам легких веществ), могут быть в ряде случаев компенсированы техническими решениями, заложенными в конструкцию преобразователя. Для создания новых конструкций кориолисовых расходомеров на основе вибрационных преобразователей расхода необходимо создание теоретической модели, описывающей законы движения элементов, функцию преобразования массового расхода в параметры движения этих элементов, причины образования погрешностей измерения и пути их минимизации.

Целью настоящей работы является получение математического выражения аддитивной погрешности измерения массового расходомера, вызванной влиянием паразитных колебаний вибрационного преобразователя массового расхода, и разработка на основе полученной формулы путей ее минимизации или исключения из результата измерений.

Краткое описание конструкции и функции преобразования. Вибрационный преобразователь массового расхода представляет собой U -образную трубку, жестко закрепленную в основании свободными концами входного и выходного участков в виде консоли. Трубка приводится в колебательное движение с частотой ω вокруг оси, проходящей вблизи жесткой заделки свободных концов. При колебаниях консольная часть трубки перемещается в вертикальном направлении со скоростью v . При движении в трубке сжатого газа на консольные участки трубки действуют знакопеременные силы Кориолиса, направленные в противоположные стороны.

Вибрационный преобразователь массового расхода изображен на рис.1.

Рис.1. Деформация вибрационного кориолисового преобразователя массового расхода под действием сил Кориолиса

На участок 1 U -образной трубки на расстоянии L 1 от оси А-А действует сила Кориолиса F k 1 , направленная против движения трубки, а на участок 2 на расстоянии L 2 от оси А-А действует сила Кориолиса F k 2 , направленная по движению трубки. Действие сил Кориолиса F k 1 и F k 2 вызывает относительное смещение по вертикали Δ х участков 1 и 2, которое можно рассматривать как угол закручивания θ вокруг оси О-О [1, 2].

Функция преобразования массового расхода Q m в смещение Δ х описывается выражением: cc kr + - + —

Q_m =A x----r-^L ,                              (1)

m

4 rtoАВ где k – жесткость участков 1 и 2 трубки при изгибе; с, с3 – жесткость участков 1, 2 и 3 при скручивании; AB – амплитуда вынужденных колебаний трубки под действием вынуждающей силы.

Колебания трубки вокруг оси А-А вызываются действием синусоидальной вынуждающей силы F В ( t ) на участок 3 в точке, лежащей на оси симметрии О-О.

Кроме колебаний вокруг оси А-А , трубка совершает вынужденные колебания вокруг оси симметрии О-О под действием знакопеременных сил Кориолиса при движении газа по трубке. Таким образом, вибрационный преобразователь расхода имеет две степени свободы [3].

Описание причины возникновения паразитных колебаний и их исследование. Если в течение жизненного цикла расходомера произойдет смещение точки приложения вынуждающей силы F В от оси О-О на расстояние Δ r , то воздействие силы создаст знакопеременный вращающий момент относительно оси О-О , как показано на рис.2.

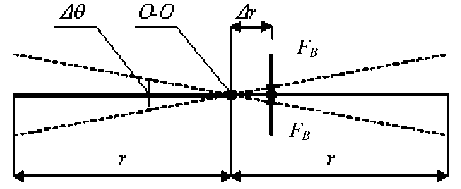
Рис.2. Колебания U -образной трубки при смещении точки приложения вынуждающей силы F_B от оси О-О на величину Δ r

Паразитные колебания трубки вокруг оси О-О , т.е. колебания, не предусмотренные конструкцией и мешающие правильной работе вибрационного преобразователя, вызванные знакопеременным вращающим моментом Δ r ∙ F B ∙sinω t , происходят и при отсутствии движения газа через нее, что вызывает наличие некоторых начальных показаний расходомера. Следовательно, паразитные колебания создают аддитивную погрешность показаний, которая не зависит от величины измеряемого расхода, а определяется величиной смещения Δ r и значением вынуждающей силы F В . Для определения погрешностей, связанных с паразитными колебаниями, рассмотрим уравнение паразитных колебаний трубки под воздействием знакопеременного момента Δ r ∙ F B ∙sinω t при наличии сопротивления движению [4]:

d 20     d0.

J —- + p— + N0 = ArFR sin гоt,(2)

dt2      dt где J – момент инерции вращения участка 3 вокруг оси О-О; р – сила сопротивления движению; N – модуль кручения трубки вокруг оси О-О.

Разделив обе части уравнения на параметр J , получим следующее выражение:

d ² 0    d 0 A rF

• —- + B— + ro20 =--- - sin го t ,                           (3)

dt2     dt    0 J где β = p/J – коэффициент затухания; (ω0)2 = N/J – квадрат частоты собственных колебаний участка 3 вокруг оси О-О.

Рассмотрим движение трубки без влияния сил сопротивления. В этом случае уравнение (3) принимает вид:

d ² 0 A rF

• —- + ron0 =---- sin гоt.(4)

dt20

Общее решение этого уравнения описывается выражением:

• 1    A rF„

0(t) = 0нач sin (ГО0t + ф) + "Г —----2sin(ГОt + Ф) .

J ГО0 -ro где Θнач – начальный угол; φ – начальная фаза.

Первое слагаемое правой части уравнения (5) определяет свободные, а второе слагаемое – вынужденные колебания трубки вокруг оси О-О . Под действием сил сопротивления свободные колебания затухают и установившееся движение представляет собой вынужденные колебания с частотой ω вынуждающей силы. Фаза установившихся колебаний при ω<ω 0 при отсутствии сил сопротивления движению мало отличается от фазы вынуждающих колебаний, поэтому формулу установившихся колебаний можно записать в виде:

A0( t ) =

1 A rF

J ® o — to

sin ( to t ) .

Выразим разность квадратов частот через отношение ω/ω 0 :

to 0

—

to

= to 0

—

to

— ^to 0 k^to 0

J

= to 0

—

to

V^to 0 7

to 0

= to 0

1 —

to to0 J

Подставив полученное выражение в (6) и применяя обратную подстановку (ω0)2 = N/J, по- лучим зависимость угла скручивания от модуля кручения N трубки вокруг оси О-О [3]:

A0( t ) =

A tF b

JN i

—

J

к

—г- sin (tot) = to2 | to2 J

A tF b

N 1 к

—

to ²

to g

sin ( to t ) .

Для определения максимального значения рассматриваемой погрешности представим амплитудное значение угла Δθ а скручивания при паразитных колебаниях, выразив при этом вынуждающую силу как произведение коэффициента жесткости k трубки при изгибе и статического смещения A B /2 в виде:

A0 а

A tF b

A rkA_H

B

N ^f 1 к

—

to ²

to 0

2 N 1 к

—

to2 i to0 J

где A B – амплитуда колебаний вокруг оси А-А; k – коэффициент жесткости трубки при изгибе вокруг оси А-А .

Модуль кручения N определяется как момент кручения U -образной трубки вокруг оси О-О , необходимый для ее поворота на угол в один радиан [3]. Исходя из этого, выразим модуль кручения N как отношение известного из (1) момента сил упругости, противодействующих силам Кориолиса, к углу скручивания θ :

A x ^f kr + c + c ³ J      kr ₊ c ₊ c 3     ,          .

N = —^к--- r—L ! _{= A} x---r—L = 2 r I kr + c + c 3 | .                (io)

0                A x        к r L J

2 r

Подставив (10) в (9), получим формулу определения амплитуды угла скручивания при паразитных колебаниях вокруг оси О-О в зависимости от коэффициентов жесткости деформируемых участков трубки:

A0 а

A rkA

B 2

Л 7      ° ^C 3 i 1 to

4 r kr + - + — 1₄

к r L Jk to 0

Вывод формулы определения погрешности от влияния паразитных колебаний. Для определения абсолютной погрешности от влияния паразитных колебаний приравняем амплитуду угла Δθ а скручивания при паразитных колебаниях к эквивалентному углу скручивания θ Q под действием сил Кориолиса при расходе Q m :

A0 a =0 Q .

Найдем зависимость угла скручивания θ от массового расхода Q m . Для этого воспользуемся формулой (1), преобразовав ее в зависимость смещения Δx от массового расхода:

к     4 Q„r to A„

A x =    --- B_

cc kr + - + — rL

Применив для упрощения дальнейших выкладок преобразование [5]

. _   А х

6 = sin 6 = —                              (14)

2r и подставив его в (13) в (14), найдем искомую зависимость угла θQ скручивания при действии сил Кориолиса:

_Q ^А х = 4 ^Q _m ^r to A b

Q r c c kr + - + — rL

•

± = 2 Q_m to A b

2r c c kr + - + — rL

.

Подстановкой (11) и (15) в (12) составим уравнение, приравняв угол скручивания трубки при паразитных колебаниях к эквивалентному углу скручивания при расходе Δ Q m , соответствующем абсолютной погрешности при паразитных колебаниях:

А rkA_H

B

л I , сс.

4 r I kr ++ —

V rL

= 2 А Q m to A b

• ²             c   c ^.

i - _ kr + - + — го2 I         r L

V ^to o 7

Решая уравнение относительно Δ Q m , получим формулу определения абсолютной погрешности от влияния паразитных колебаний:

А Q m

I C    C.

А rkA„ I kr +1--

B

V r L

А r

8 rroA_B I kr + c + c ³ I 1 B V r L

—

V

J

^ш о 7

r

•

k

•

8® I

V

—

?)

^ш о 7

Определим приведенную погрешность как отношение абсолютной погрешности к верхнему пределу измерения, выраженному функцией преобразования при Q max :

А r

•

r

k

-----------•

8 to

А Q

Y = ^m

Q max

¹ — ^I

V ^to o 7   ^{А r}

-------------:-- = ----- •

k

•

А 1 1 , с    с 3 I      r _n , с    c ₃ I ₁

— I k +— 2 +I 2 toА 1 I k +— 2 +I 1

4 V r rL у               V r rL 7

—

' 100% .

to to0

Преобразуем отношение коэффициентов жесткости, выразив их через упругие постоянные и моменты инерции сечений участков 1, 2 и 3:

k

cc k I . I — r2 rL

3 EJ p

2 L ³

( 3       2 I EJ

2 L ? ⁺ 2 r² ( 1 + ц ) J

,

1 + ² 1 L I ( 1 + ц )

3 V r 7

где µ – коэффициент Пуассона материала трубки.

Выполнив подстановку в (17) преобразованного отношения коэффициентов жесткости (18) и выражения временного интервала как отношения Δ t = φ max /ω , получим окончательное выражение для определения приведенной аддитивной погрешности, связанной с влиянием паразитных колебаний в системе без сопротивления движению:

А r 1

Y =------ r  2^max

•

1 + 2 1 L ^{| 2}

3 V r 7

•

- 100% .

to

¹      2

^to 0

Правый сомножитель в полученной формуле для колебательной системы без сопротивления движению равен отношению амплитуды угла Δθ а к статическому углу Δθ ст при постоянном значении силы F B :

АО а =    1    .

^АО ст 1 ю 2 .

¹ - ~2

В системе с трением это отношение учитывает также влияние сил сопротивления движению, выражающееся коэффициентом затухания β , и определяется по формуле [4]:

АО а

АО ст

to I

+ 4

<^Ю 0

£] ;tol к ^to 0 ) к ^to 0 )

Так как в механической колебательной системе всегда присутствуют силы сопротивления движению, то соответствующее выражение для приведенной погрешности измерения расхода от паразитных колебаний в системе с трением имеет вид:

Y =

r

А r   1

² Ф тах

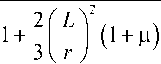
1 -к

to ²

to 0

+ 4

k^to o

to I

k^to 0

• 100% ,

где первый сомножитель правой части - относительное смещение точки возбуждения колебаний, второй сомножитель - коэффициент, учитывающий влияние угла сдвига фаз колебаний входного и выходного участков, третий сомножитель – относительная жесткость вибрационного преобразователя, четвертый сомножитель – соотношение динамической и статической амплитуд вибрационного преобразователя.

Исследование влияний составляющих погрешности. Параметром, образующим погрешность, является относительное смещение Δ r / r , которое зависит от смещения точки приложения вынуждающей силы от оси симметрии U -образной трубки и всегда присутствует в реальных конструкциях. Поскольку погрешность связана с относительным смещением линейной зависимостью, она может быть сведена к минимуму юстировкой положения возбудителя колебаний относительно оси симметрии О-О либо исключена из результата измерений схемотехническими или алгоритмическими методами.

Остальные параметры в уравнении (21) являются коэффициентами, влияющими на величину погрешности измерения расхода.

Влияние угла сдвига фаз колебаний входного и выходного участков. Угол сдвига фаз φ зависит от измеряемого расхода. Относительная погрешность связана со сдвигом фаз обратной зависимостью и достигает своего минимума при максимальном угле сдвига фаз, ограниченном сверху значением, при котором переменная величина ω А B cosω t изменяется в достаточно узких пределах, допустимых при аппроксимации постоянной величины скорости ω А B . Максимум погрешности достигается при минимальном значении угла сдвига фаз, ограниченного разрешающей способностью схемы выделения временного интервала между одинаковыми фазами колебаний входного и выходного участков трубки.

Влияние относительной жесткости зависит от соотношения размеров L и r . При длине участков L , превышающих длину плеча r в n раз, погрешность уменьшается приблизительно в (1+0,858 n ²) раз. Если r превышает длину L , то относительная жесткость трубки асимптотически приближается к единице, оказывая меньшее влияние на уменьшение погрешности.

Влияние соотношения динамической и статической амплитуд (20) на погрешность зависит от отношения частот ю/ю₀. При частоте собственных колебаний © о , намного превышающей частоту вынужденных колебаний ©, отношение амплитуд близко к единице и не оказывает влияния на погрешность. При приближении частоты вынужденных колебаний к частоте собственных колебаний отношение амплитуд увеличивается, вызывая увеличение погрешности. При равенстве частот ю=ю₀ отношение амплитуд резко возрастает, вызывая резкий рост погрешности, что связано с явлением резонанса колебаний. Для исключения явления резонанса отношение частот ю/ю₀ не должно превышать 0,2.

Заключение. Полученное выражение приведенной погрешности измерения массового расхода от паразитных колебаний U -образной трубки дает возможность рассчитывать ее значение при определении суммарной погрешности массового расходометра. Кроме того, полученная формула позволяет оптимизировать соотношение геометрических размеров U -образной трубки с целью снижения погрешности при проектировании расходомера.