Исследование влияния скорости воздушного потока на собственное аэродинамическое сопротивление ленточной подвески в аэродинамической трубе Т-102 ЦАГИ

Комплексное использование вычислительных и экспериментальных методов является наиболее актуальным способом получения аэродинамических характеристик (АДХ) летательных аппаратов (ЛА) на. сегодняшний день [1], [2], [3]. Так, эксперимент является основным источником данных, необходимых для валидации математических моделей [4], [5],

а расчетные методы, в свою очередь, могут служить инструментами решения задач методического обеспечения эксперимента, например, с помощью методов вычислительной аэродинамики [6], [7], [8]. В [9], [10], [11] определяется влияние границ потока на АДХ профиля крыла при испытаниях в АДТ малых скоростей с открытой рабочей частью. Влияние стенок на обтекание моделей в АДТ с закрытой рабочей частью исследуется в [12] и с перфорированной в [13], [14], [15]. Большое количество работ посвящено задаче исследования влияния поддерживающих устройств на результаты экспериментальных исследований: хвостовой [16], [17], [18], килевой [19] и других типов [20], [21] державок; ленточной подвески [22], [23]. Этой задаче, применительно к ленточной подвеске в АДТ Т-102 ЦАГИ, посвящена настоящая работа.

АДТ Т-102 предназначена для исследования аэродинамических характеристик моделей самолетов на режимах взлета, посадки и малых скоростей полета (рис. 1). Крепление модели в рабочей части аэродинамической трубы при использовании измерительной системы АВ-102 производится в трех точках. Эти точки образуют равнобедренный треугольник, основанием которого является поперечная (крыльевая) база L_z, а высотой - продольная база L_x (рис. 2). Поперечная база имеет размеры L_z = 0.25; 0.4; 0.6; 0.8; 1.0; 1.2; 1.5 м, а продольная L_x = 0.4; 0.6; 0.75; 0.9 м. Аэродинамические нагрузки посредством элементов подвески передаются на автоматические шестикомпонентные весы, смонтированные на раме вне воздушного потока. Поэтому результаты испытаний моделей в АДТ Т-102 при использовании измерительной системы АВ-102 содержат силы и моменты, действующие как на модель, так и на подвесное устройство, а значит, влияние последнего необходимо исключить из результатов испытаний путем внесения соответствующих поправок на аэродинамические силы и моменты подвески.

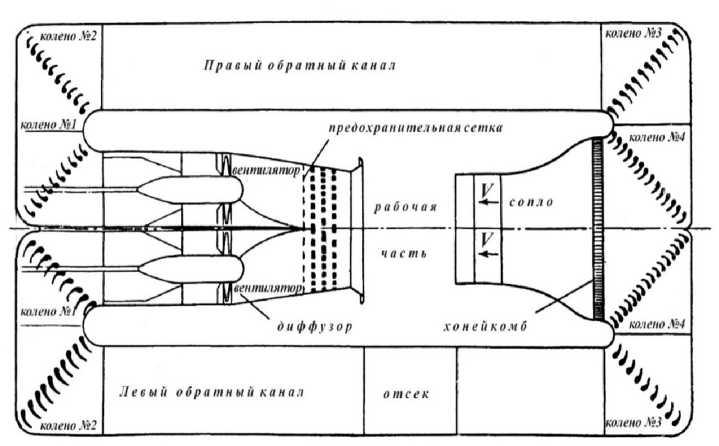
Рис. 1. Схема. АДТ Т-102

Методика, учета, влияния поддерживающих устройств на. результаты испытаний в АДТ Т-102 изложена, в [24]. Согласно этой методике, аэродинамические характеристики ленточной подвески определяются экспериментально по испытаниям подвески, на. которой вместо модели устанавливается профилированная распорка, (рис. 3), представляющая собой аэродинамическую модель прямого крыла с симметричным профилем. На распорках установлены кронштейны крепления к поперечной базе, охватывающие переднюю кромку. Крепление на продольных базах Lx обеспечивается через цилиндрическую державку, охватывающую заднюю кромку, на которой нанесена резьба для соединения с кронштейнами крепления различной длины. Испытания проводятся при скоростях потока, от 15 до 50 м/с при нулевом угле атаки. Процедура, определения АДХ выполняется каждый раз при замене подвески, выработавшей свой ресурс. Расхождение АДХ подвесок, выполненных по одним и тем же чертежам, объясняется как отступлениями в геометрии профиля при изготовлении лент [23], так и некоторой разницей в ориентировке лент подвески относительно весовых осей координат. Поправка на аэродинамические характеристики подвески вычисляется путем вычитания АДХ изолированной распорки из характеристик системы «распорка+подвеска». Для определения аэродинамических коэффициентов самих распорок проводились специальные испытания подвески с распоркой и той же подвески со штангой, закрытой обтекателем [24]. В результате этих исследований были получены силы, действующие на распорки в окрестности скорости 50 м/с, в которой и проводится основная масса весовых экспериментов на сегодняшний день.

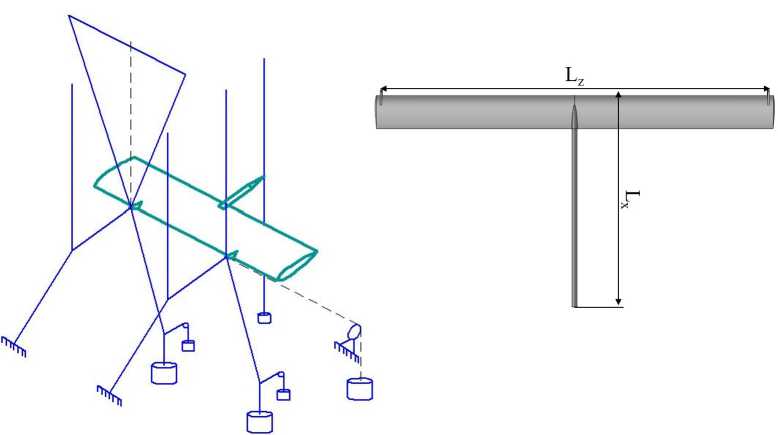
Рис. 2. Схема крепления распорки в АДТ Т-102 ЦАГИ при использовании измерительной системы

АВ-102

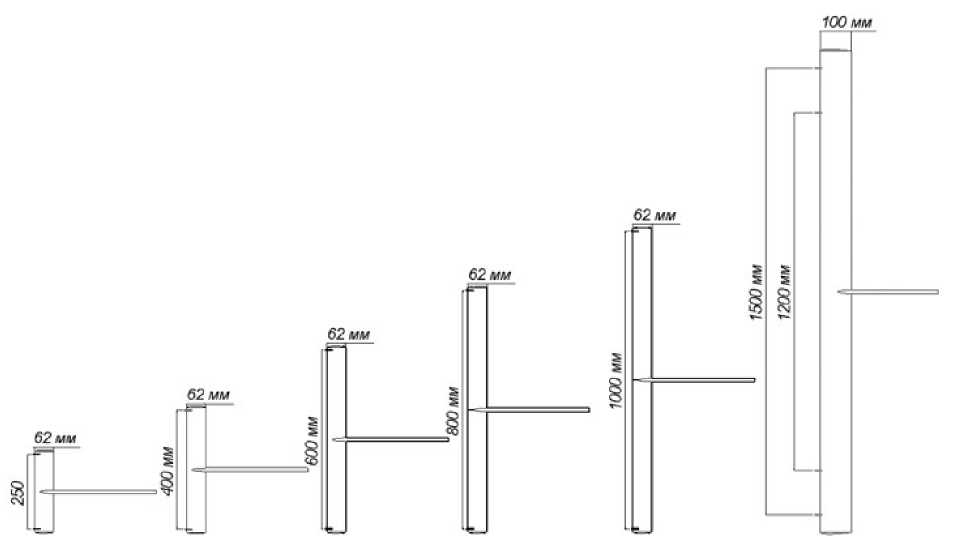
Рис. 3. Схемы исследуемых распорок

Бурное развитие малоразмерных ЛА [25], [26], [27], [28], [29], а также летательных аппаратов на солнечных батареях [30], [31], [32], [33], которые преимущественно используют малые скорости полета, приводит к необходимости обеспечивать экспериментальные исследования в диапазонах чисел Рейнольдса порядка Re 103... 105 (рис. 4). Соблюдение подобия по данному критерию возможно с помощью перехода на более низкие скорости воздушного потока в АДТ. В [34] была обнаружена неучтенная систематическая погрешность в опреде- лении аэродинамического сопротивления модели БЛА при переходе на меньшие скорости воздушного потока: V = 20, 25 м/с и обнаружено, что эта погрешность связана с существенным увеличением сопротивления распорок при уменьшении скорости воздушного потока. Было предложено ввести поправку в виде зависимости коэффициента аэродинамического сопротивления распорок от скорости воздушного потока (числа Рейнольдса), которая была принята одинаковой для всех распорок. Такой подход позволил получить приемлемые АДХ исследуемой модели [35]. Однако в расчете поправки [34] был принят профиль NACA0012 с толщиной задней кромки, равной измеренной на одной из распорок. В реальности при изготовлении распорок Lz = 0.25; 0.4; 0.6; 0.8; 1.0 за исходный был принят симметричный профиль В с относительной толщиной 12%. Его аэродинамические характеристики при Re = 1.7 • 105 были исследованы в работе [36]. Внешний осмотр распорок показал, что толщина задней кромки составляет около 1 мм, в то время как теоретическая форма профиля (рис. 5) имеет острую заднюю кромку. Кроме того, реальная геометрическая форма распорок неизбежно отличается от теоретической за счет погрешностей при изготовлении [37].

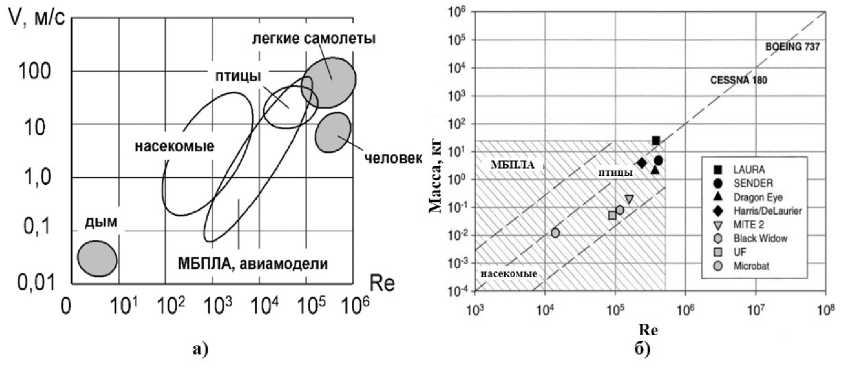
Рис. 4. Диапазон эксплуатационных чисел Рейнольдса, характерных для малоразмерных ЛА: а) [38], б) [39]

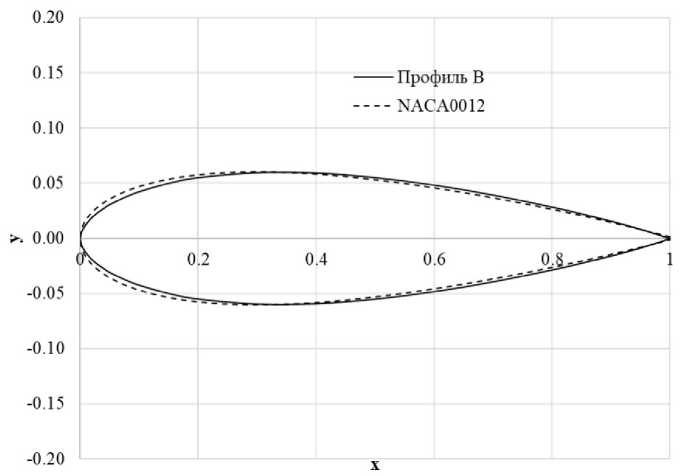
Рис. 5. Теоретическая форма, симметричного профиля В [36] и NACA0012

Целью настоящей работы является определение влияния скорости воздушного потока на собственное аэродинамическое сопротивление ленточной подвески в АДТ Т-102 ЦАРИ для внесения поправки в результаты эксперимента. Для определения величины поправки было предложено:

• 1)    построить математическую ЗП-модель распорок с помощью измерений координат точек на их поверхности;

• 2)    провести расчетные исследования влияния скорости воздушного потока на аэродинамическое сопротивление распорок с использованием полученной ЗП-модели.

2.    Измерения координат точек поверхностей распорок с помощью координатно-измерительной машины 3.    Автоматическая постобработка результатов измерений

Первая задача относится к обратному инжинирингу, который часто применяется в машиностроении [40], [41]. Для построения математических ЗП-моделей проводились измерения координат точек на поверхности контрольных сечений распорок с применением высокоточной координатно-измерительной машины (КИМ) LK G90-C. Измерения проводились при Т = 21 °C с точностью ±0.005 мм. Методика использования таких КИМ для оценки точности изготовления аэродинамических моделей отработана в ЦАГИ и описана в [42].

В качестве начального приближения строились ЗВ-модели с использованием фиксированного профиля по размаху, которые корректировались по результатам измерений. Количество профилей сечений плоскостью ХҮ в зависимости от размаха распорок составляло от 6 (для L_z = 0.25 м) до 34 (для L_z = 1.5 м). Для каждого сечения измерялись координаты 200 точек его профиля.

Постобработка результатов измерений была реализована в программе RasporkaParser и включала в себя:

• 1)    сортировку измеренных точек;

• 2)    вычисление пространственного положения каждого сечения относительно связанной с распоркой системы координат (СК);

• 3)    вычисление размерной хорды профиля каждого сечения;

• 4)    аппроксимацию относительных координат профиля;

• 5)    вывод результатов постобработки.

Пространственное положение профилей сечений определялось координатами точек в связанной с распоркой СК, находящихся на четверти местной хорды сечения и углами поворота связанных с профилями систем координат. Длина хорды вычислялась как разность величин максимальной и минимальной координаты х в связанной с профилем СК.

Предварительный анализ результатов измерений показал, что профили являются близкими к симметричным, как и теоретические, на основе которых были спроектированы распорки. Поэтому было предложено использовать полиномиальную зависимость как у симметричных профилей NACA [43], но более высокого порядка:

У = ±

^ о о Дж + ^ a_k х^к^

= ± ^ ^к х^Рк , к=0

^гД^е Рк={0.5, 1, 2, 3, 4, 5, 6, 7, 8}, к = 0..8; х и у - относительные координаты профиля, а_к - коэффициенты полинома.

Вычисление коэффициентов а^ производилось методом наименьших квадратов. Для этого решалась линейная система из 9 уравнений (n = 0...8):

'8

ЕЕак хрх? = Е Ых?, к=0  іі

...

* Е ЕакхРікхТ = Е ЫхГ, к=0  іі

...

ЕЕ ак х” ■. = Е 1»‘|хТ

.. к=0   іі где Хі и уі - результаты измерений координат точек профиля.

Пример аппроксимации приведен на рис. 6. Такой подход позволил получить среднеквадратичное отклонение (СКО) координаты у, не превышающее 0.13% (рис. 7).

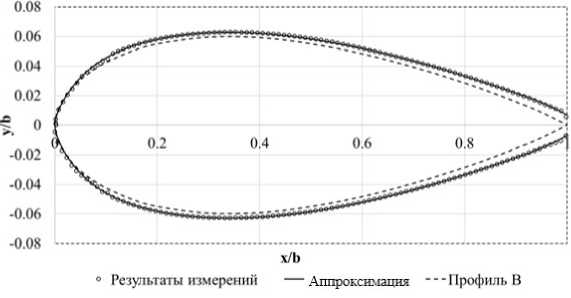
Рис. 6. Результаты постобработки одного из сечений в связанной с профилем системе координат

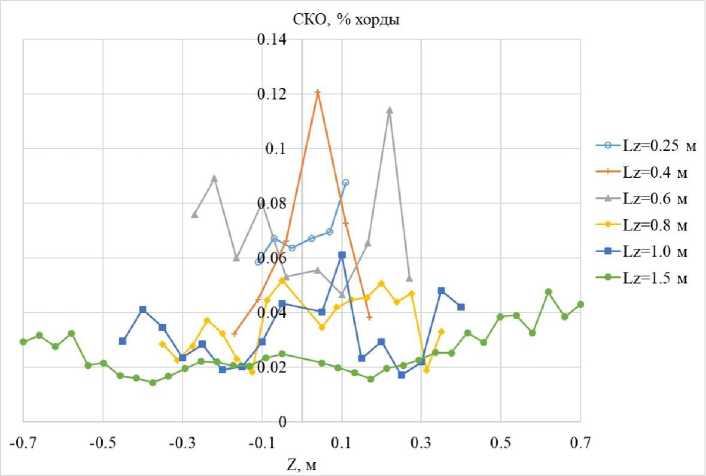
Рис. 7. СКО координаты у аппроксимации профилей сечений распорок от результатов измерений

4.    Результаты определения геометрических форм распорок

Результаты автоматической обработки данных измерений приведены на рис. 8-11. СКО геометрических параметров, приведенных на рис. 8 и 9, характеризуют погрешность изготовления распорок. Величина среднеквадратичного отклонения составляет 0.16... 0.7% длины хорды и 0.02... 0.12% относительной толщины профиля в зависимости от распорки. Наибольшие величины СКО характерны для распорки L_z = 0.6, а наименьшие для L_z = 1.5. На рис. 10 и 11 приведены параметры, характеризующие угол поперечного V и геометрическую крутку соответственно. Видно, что смещение сечений относительно корневой хорды не превышают 0.7 мм, а геометрическая крутка отдельных сечений может достигать 0.6° (распорка L_z = 0.8 м).

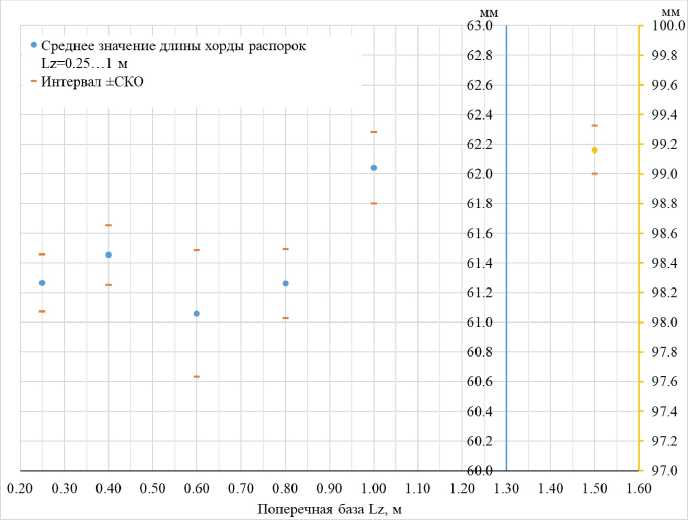
Рис. 8. Среднее значение длины хорды распорок

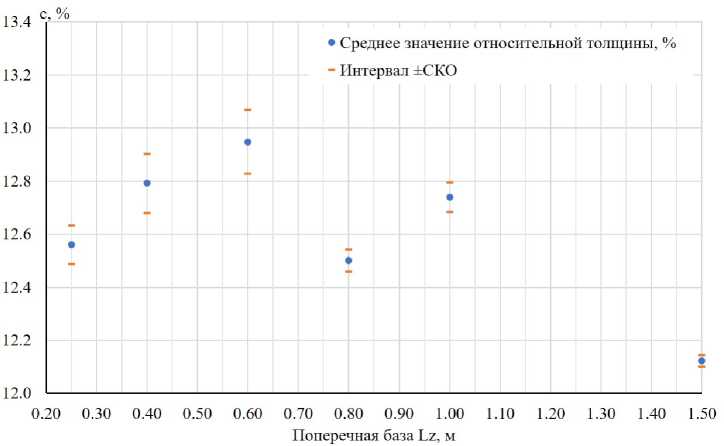
Рис. 9. Средние значения относительной толщины профилей распорок

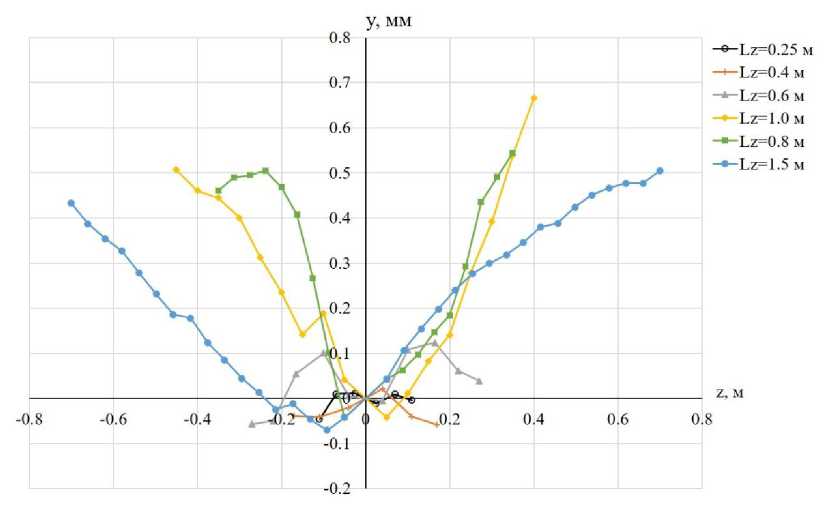
Рис. 10. Координаты точки 25% хорды сечений в связанной с распоркой СК

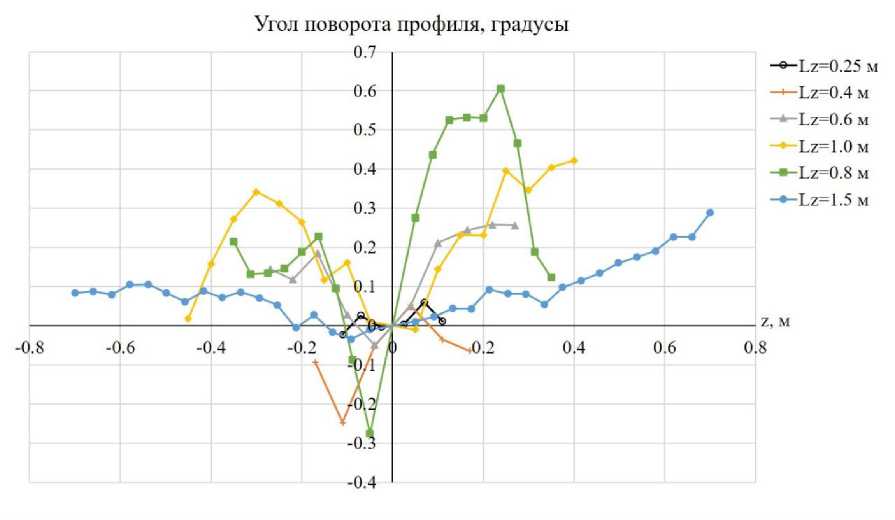
Рис. 11. Геометрическая крутка, относительно оси, проходящей через 25% корневой хорды

5.    Расчетные исследований АДХ распорок с использованием программы XFLR5

Расчет АДХ распорок производился в программе XFLR5 [44] методом вихревой решетки - VLM (Vortex Lattice Method). Вычисления производились при числе Маха М = 0, скоростях воздушного потока V = 10; 15; 20; 25; 30; 35; 40; 45; 50; 55 м/с, при а = 0° и 3 = 0°. Диапазон чисел Рейнольдса при указанных скоростях составлял Re = 0.4... 2.5-10⁵ для распорок L_z = 0.25; 0.4; 0.6; 0.8; 1.0 м и Re = 0.6... 4.1-10⁵ для распорки L_z = 1.5 м.

В программе XFLR5 используется модель «eNtr» ламинарно-турбулентного перехода (ЛТП). Величина А-фактора была вычислена по эмпирической зависимости [45], [46]:

A_tT = -8.43 - 2 . 41п( е ) .                                  (1)

В качестве исходных данных были приняты результаты измерения степени турбулентности продольной компоненты скорости воздушного потока е_п, полученные в АДТ Т-102 с помощью измерений термоанемометром в 1977 г. (рис. 12) под руководством Л. И. Илизаровой. Эти измерения показали, что:

• 1)    наличие модели в АДТ пренебрежимо слабо влияет на степень турбулентности;

• 2)    степень турбулентности слабо изменяется в диапазоне скоростей 20. .. 50 м/с;

• 3)    при 15 м/с степень турбулентности значительно больше, чем при остальных исследованных скоростях.

0.07 0.05 о.оз 0.01

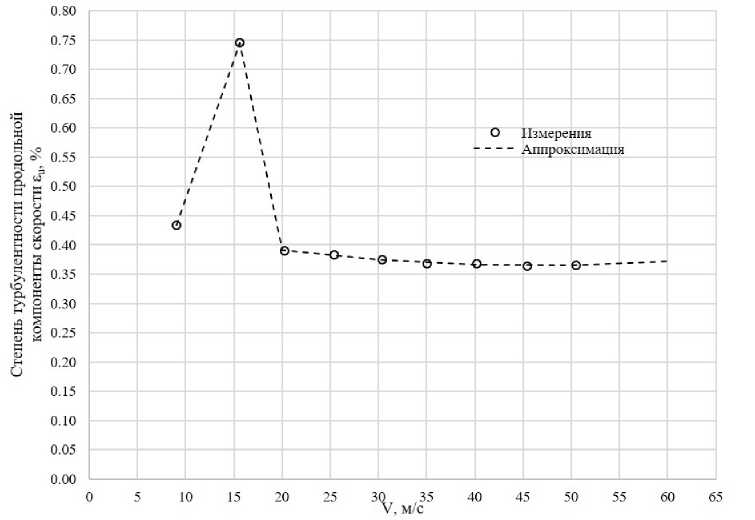
Рис. 12. Степень турбулентности АДТ Т-102

В диапазоне скоростей V = 20 ... 60 м/с для получения степени турбулентности использовалась аппроксимация квадратичной зависимостью, а при V < 20 м/с кусочно-линейная интерполяция. Величина А-фактора при таких значениях е в исследуемом диапазоне скоростей изменяется в пределах А _tT = 3.33... 5.04.

В методе VLM в качестве исходных данных для расчета АДХ крыла используются аэродинамические характеристики профилей сечений. Эти характеристики были получены с помощью программы XFOIL [47], [48], [49], которая интегрирована в XFLR5. Для исследования сходимости профильных характеристик в XFOIL были проведены расчеты профиля сечения Z = -0.25 мм, координаты которого были заданы с помощью п = 57, 113, 169, 225, 281 точек, что соответствовало нормированному количеству Һ = 225/п = 4.93, 2.49, 1.66, 1.25, 1. В качестве иллюстрации на рис. 13 приведены координаты профиля для самого грубого и самого мелкого шага точек. Результаты этих исследований для коэффициента сЖа и координаты точки ламинарно-турбулентного перехода xtT приведены на рис. 14. Они показывают, что уменьшение Һ (увеличение количества точек) приводит к незначительному влиянию на результат вычисления (АсЖао < 0-0001, Аж^г < 0.0055). Поэтому в расчетах использовалось описание профиля 57 точками (Һ = 2.22).

-0.01

-0.03

-0.05

-0.07

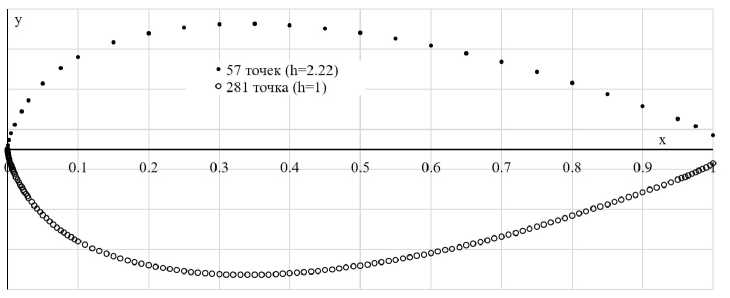
Рис. 13. Координаты профиля для исследования сходимости по сетке в XFLR5

Для валидации подходят данные работы [50], в которой рассматривается схожий тестовый случай. Авторами Counsil J.N.N. и Goni Boulama К. в диапазоне чисел Рейнольдса Re = 0.48... 2.5 105 для симметричного профиля NACA 0012 проведено сопоставление результатов расчета, полученных с помощью XFLR5 версии 6.02, других расчетных методов, а также экспериментальных данных. Характерной проблемой, которая усложняет расчетные исследования в данном диапазоне чисел Рейнольдса, является формирование ламинарного «пузыря» [38], [51], [52] - LSB (laminar-separation-bubble) [53], [54], [55], [56], который представляет собой локальный ламинарный отрыв потока с дальнейшим присоединением, вызванным ламинарно-турбулентным переходом на поверхности профиля (рис. 15). Интерес к исследованию LSB связан с тем, что его форма и размеры оказывают существенное влияние на аэродинамические характеристики несущих поверхностей [57], [58], изменяя их «эффективную» геометрию. Поэтому в [50] большое внимание уделено в том числе точности получения параметров ламинарного «пузыря». Counsil J.N.N. и Goni Boulama К. высоко оценивают результаты расчетов в программе XFLR5 с точки зрения точности при низких ресурсозатратах.

В отличие от настоящей работы, в [50] для вычисления N-фактора использовалась следующая зависимость:

Ж = 2.13 - 6.18 ln(e). (2)

На рис. 16 приведено сравнение N-фактора, полученного с помощью формул (1) и (2). Можно увидеть, что в диапазоне степеней турбулентности Ае = 0.02... 0.4% разница в величине Nr лежит в диапазоне AN_г = ±5%. Увеличение степени турбулентности е > 0.4% приводит к возрастанию AN. Так, при е = 1% величина AN составляет 23%. Между использованием зависимостей (1) и (2) и версиями XFLR5 6.02 и 6.58 не наблюдается существенных различий для тестовых случаев [50] (рис. 17-18).

6.    Профильные АДХ

На рис. 19 показаны графики зависимости коэффициента подъёмной силы и лобового сопротивления от скорости воздушного потока, вычисленные в программе XFLR5 для распорки L_z = 0.8 м, имеющей наибольшие величины погрешности геометрической крутки.

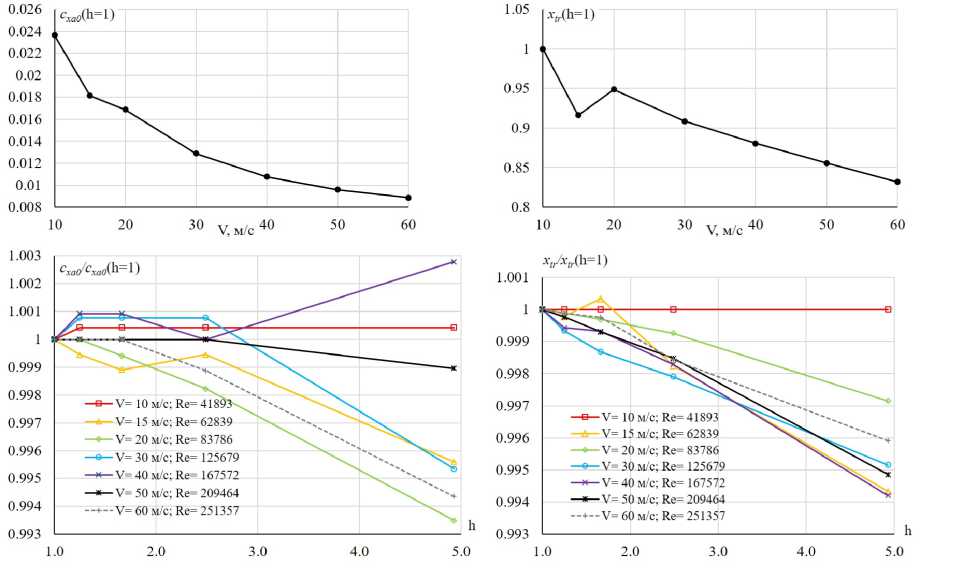
Рис. 14. Результаты исследования сходимости по количеству точек профиля в программе XFLR5

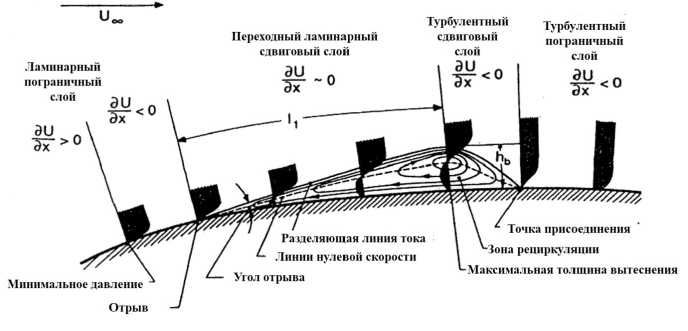
Рис. 15. Структура LSB [58]

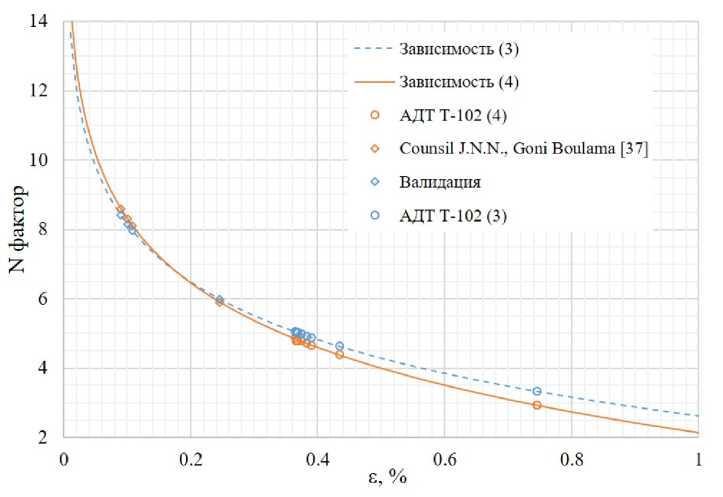
Рис. 16. Сравнение N_tr для зависимостей (1) и (2)

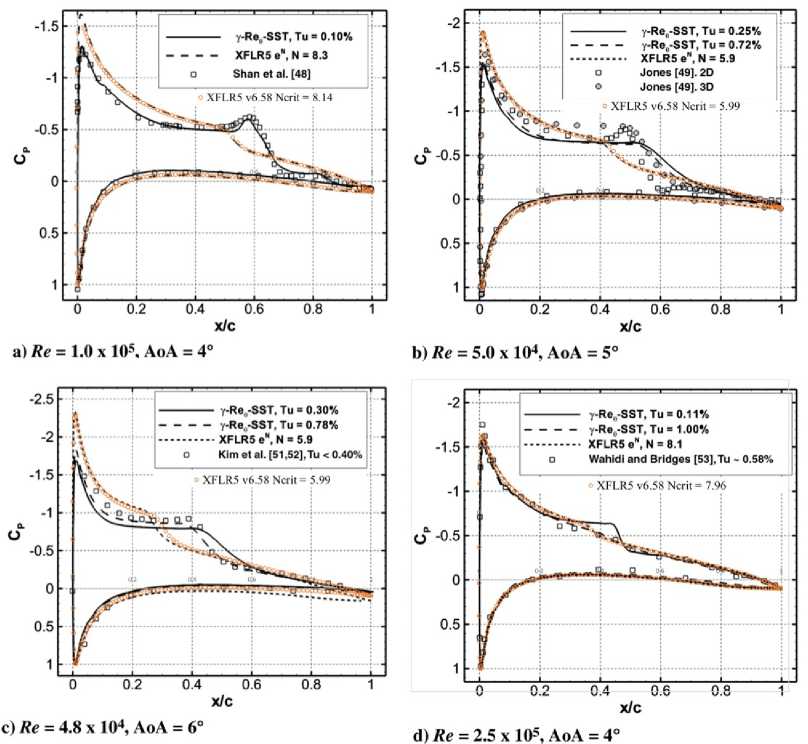
Рис. 17. Распределение коэффициента давления ср по хорде профиля

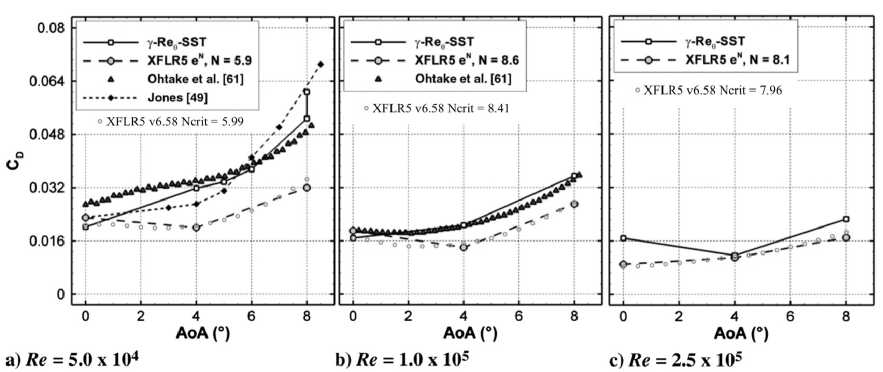
Рис. 18. Коэффициент лобового сопротивления cq

Для большей точности использовалось описание профиля, соответствующее нормированному количеству точек Һ = 4.93 (225 точек).

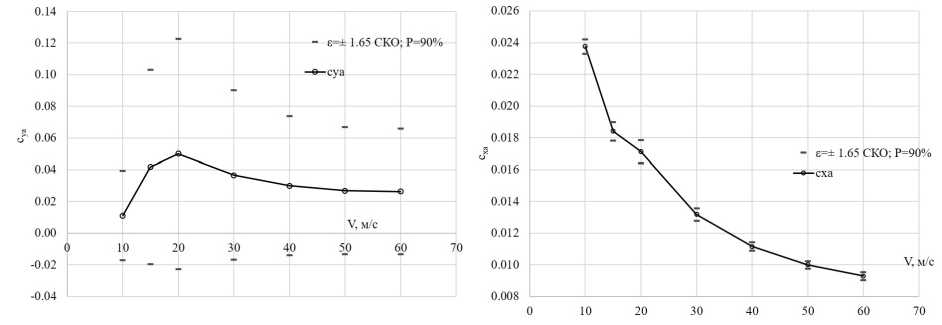
Рис. 19. Результаты осреднения расчетных значений сУа и сЖа распорок

Аэродинамические характеристики представлены в виде осредненных по 18 профилям значений и интервалов, соответствующих доверительной вероятности Р = 90% (±1.65 СКО), который характеризует отклонение от среднего. При расчёте учитывалось:

• 1)    изменение числа Рейнольдса, вызванное отличием хорды профилей;

• 2)    изменение угла атаки профиля, вызванное наличием погрешности в виде геометрической крутки (рис. 11) и различие в форме профиля (рис. 8-9).

7.    Расчетные исследования интегральных АДХ распорок

Погрешность изготовления распорки приводит к возникновению ненулевого коэффициента подъёмной силы, максимальное значение которого достигается при скорости воздушного потока V = 20 м/с. Анализ распределения коэффициента трения су по верхней поверхности профиля (рис. 20) показывает, что при V = 30 м/с и ж ^ 0.79. . . .0.9 формируется ламинарный «пузырь»: отрыв потока (су < 0, ж ~ 0.79) с дальнейшим ламинарнотурбулентным переходом (ж^_г ~ 0.89) и присоединением (ж ~ 0.9). Возникающая при этом зона отрывного «пузыря» увеличивается с уменьшением скорости воздушного потока и из всех исследованных режимов при 20 м/с имеет наибольшую длину (0.76 С ж С 0.97). Увеличение степени турбулентности в АДТ при V = 15 м/с приводит к более раннему ЛТП и уменьшению длины LSB по сравнению со скоростью V = 20 м/с (рис. 20). Наличие отрывного пузыря создает эффект, качественно схожий с увеличением кривизны профиля, и приводит к дополнительному увеличению с_Уа, с чем и связано наибольшее значение коэффициента подъемной силы при V = 20 м/с. При дальнейшем снижении скорости при 15 м/с переход происходит раньше за счет повышенной е_м, а при 10 м/с поток уже не присоединяется после отрыва, что приводит к потере части подъемной силы. Среднее значение точки ЛТП при этой скорости находится вблизи задней кромки (ж^_г = 0.95, рис. 20). Небольшое смещение вниз по потоку ж^_г за счет отклонений в геометрии может приводить к тому, что присоединения потока не произойдет и отрыв потока распространится на всю заднюю кромку (ж > 0.76). Эта высокая чувствительность к малым изменениям геометрии отражается в наибольшей величине отклонений при данной скорости от среднего для коэффициентов аэродинамических сил, которые составляют Дс_Уа = ±0.0051 (±145%) и Ас^ = ±0.0038 (±4.2%/.

Вычисления производились с учетом аэродинамической, геометрической крутки и местного угла «V». Кронштейны крепления и законцовки не моделировались. В качестве примера исходные данные для расчета распорки Д == 0.25 приведены на рис. 21.

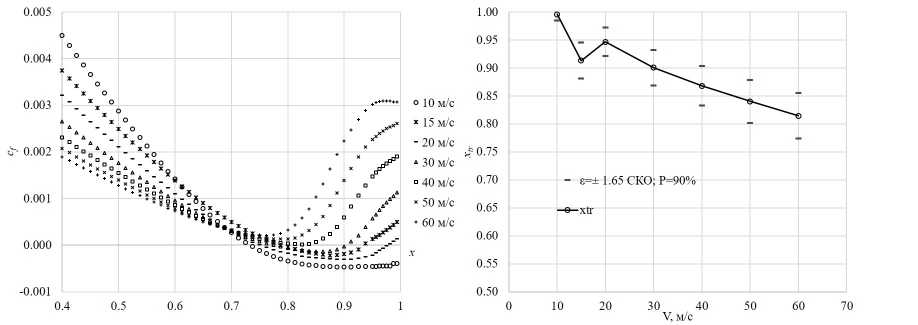
Рис. 20. Результаты осреднения распределения коэффициента трения су по хорде профиля и координаты ЛТП

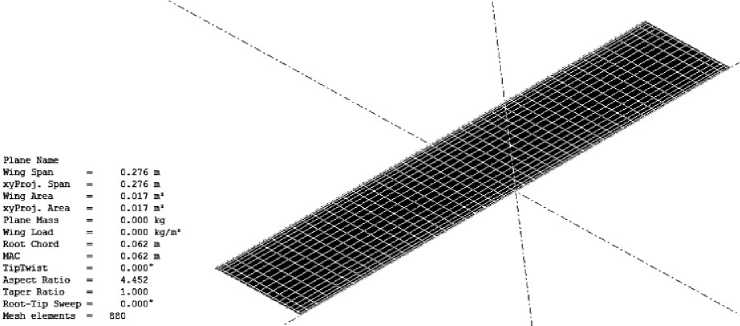
Рис. 21. Пример исходных данных в XFLR5

о Lz= 0.25

• □ Lz= 0.4

Д Lz= 0.6

x Lz=0.8

+ Lz= 1.0

• -^- Lz= 1.5

0.8 м

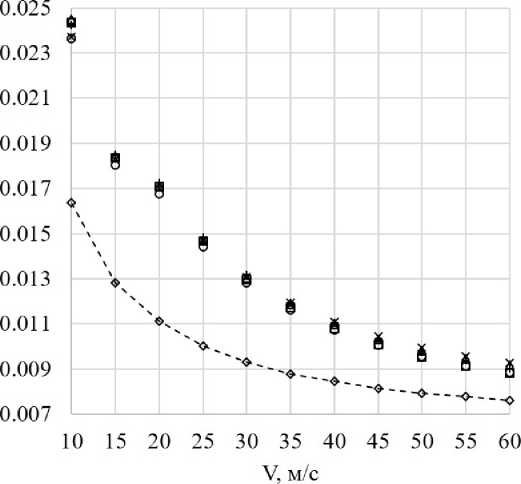
Рис. 22. Результаты расчетных исследований лобового сопротивления распорок с помощью XFLR5

Результаты расчетов аэродинамического сопротивления распорок при a = 0° приведены на рис. 22. Они показывают, что уменьшение скорости воздушного потока (числа Рейнольдса) вызывает рост коэффициента аэродинамического сопротивления распорок при a = 0°. Такое поведение с_Ха связано с тем, что толщина пограничного слоя увеличивается при уменьшении числа Рейнольдса. В качестве примера на рис. 23 приведены распределения толщины вытеснения (как характеристики толщины пограничного слоя) по хорде при исследуемых скоростях воздушного потока для профилей распорок L_z = 0.8 и L_z = 1.5 м. Видно, что при одинаковых скоростях, на профиле распорки L_z = 1.5 м пограничный слой тоньше за счет больших чисел Не, поэтому именно данная распорка обладает наименьшим коэффициентом аэродинамического сопротивления. Менее интенсивный рост коэффициента сопротивления с уменьшением скорости воздушного потока у распорки L_z = 1.5 м связан с более благоприятной формой профиля, благодаря чему отрывной «пузырь» формируется только при V = 10 м/с (cf < 0, 0.66 С ж СО.9), в то время как при сопоставимых числах Re на профиле L_z = 0.8 точка присоединения находится вблизи задней кромки профиля (рис. 24).

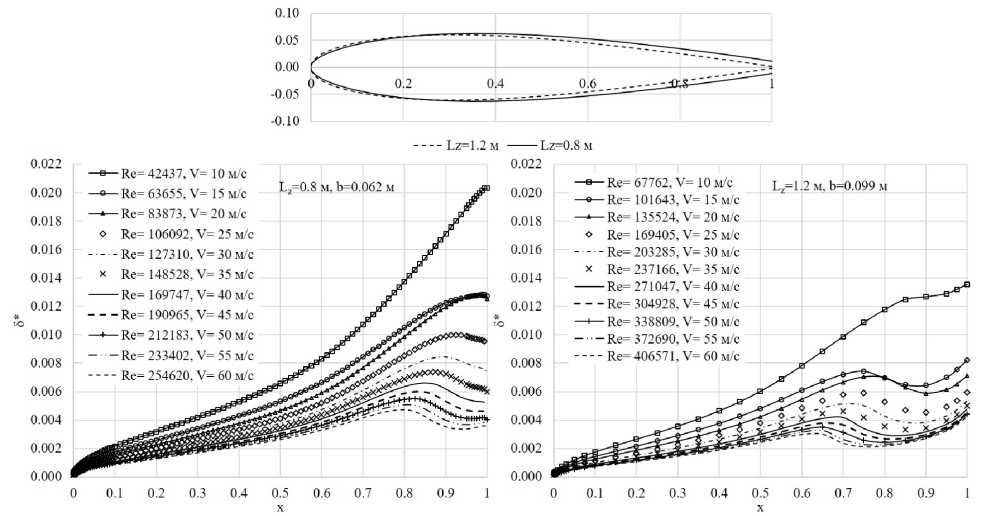
Рис. 23. Распределение толщины пограничного слоя по хорде профилей распорок Lz и Lz = 1.2 м

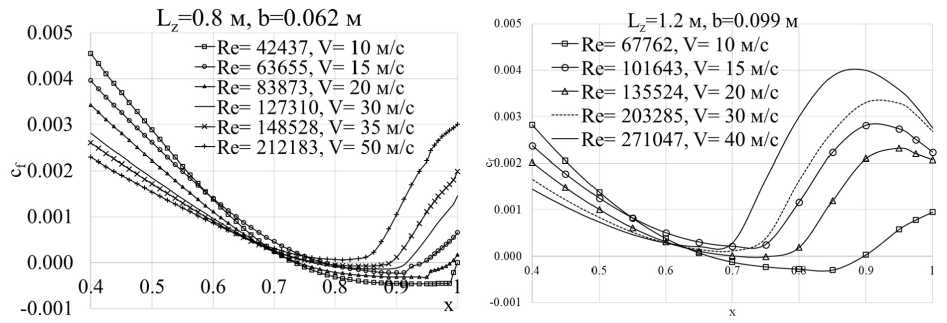
Рис. 24. Распределение коэффициента трения по хорде профилей распорок Lz = 0.8 ми Lz = 1.2 м

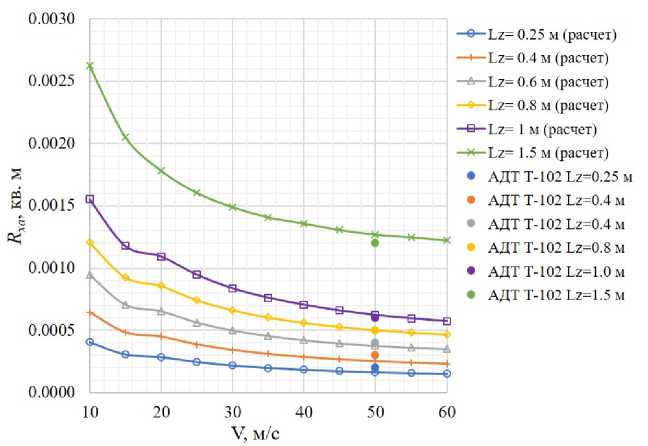
На практике для удобства вычисления поправки в АДТ вместо коэффициента лобового сопротивления распорки используется величина R_Xa, которая представляет собой отношение аэродинамической силы F_Xa к скоростному напору q:

Ғ

⁷_Ха — ""^— — с_ха — с_Ха S — [м ].

Значения ДХа распорок, полученные расчетным путем, в сравнении с данными, принятыми в АДТ для вычисления собственного сопротивления ленточной подвески, приведены на рис. 25. Видно, что /іД хорошо согласуются при скорости 50 м/с с данными АДТ. Размерная величина ошибки определения силы аэродинамического сопротивления распорки, которая является разностью между данными АДТ и результатами расчета, приведена на рис. 26. Возникновение экстремумов в данной зависимости определяется ростом скоростного напора с увеличением скорости воздушного потока и ростом коэффициента аэродинамического сопротивления с ее уменьшением. Максимальное значение ошибки лобового сопротивления для распорки Lz — 1.5 м достигается при заметно большей скорости воздушного потока, чем для остальных распорок. Это обусловлено существенными различиями в зависимости сха(У), вызванными разницей как в геометрии профиля, так и в реализуемом диапазоне чисел Рейнольдса.

Lz— 0.25 м (расчет)

Lz= 0.4 м (расчет) lz— 0.6 м (расчет) Lz= 0.8 м (расчет) Lz 1 м (расчет) Lz= 1.5 м (расчет) АДТ Т-102 Lz-0.25 м АДТ Т-102 Lz=0.4m АДТ Т-102 Lz=0.4m АДТ Т-102 Lz-0.8 м АДТ Т-102 Lz=1.0m АДТ Т-102 Lz-1.5 м

0.0030

0.0025

0.0020

“ 0.0015

Д

0.0010

0.0005

0.0000

30      40

V, м/с

Рис. 25. Значения ДХа распорок

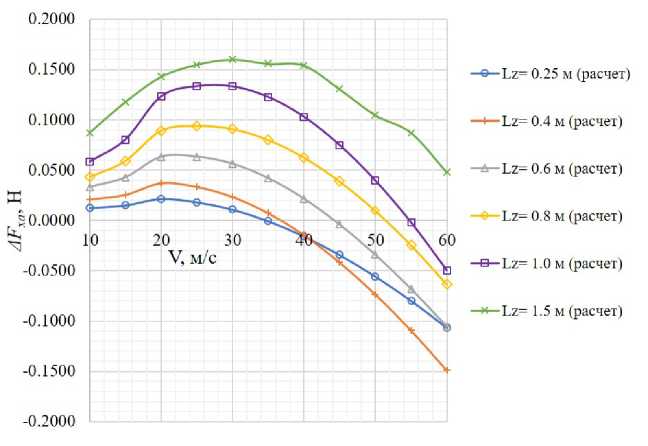
Рис. 26. Размерная величина, погрешности

В технических требованиях [59] указано, что площадь крыла моделей, предназначенных для испытаний в данной АДТ, не должна превышать S = 0.8 м². Следовательно, вычислив погрешность коэффициента лобового сопротивления относительно данной площади, получим нижнюю оценку систематической ошибки определения коэффициента с_Ха (рис. 27). Это означает, что такая систематическая погрешность Ас_Ха будет тем больше, чем меньше характерная площадь исследуемых моделей. Из рис. 27 видно, что при уменьшении скорости воздушного потока V ниже 25 м/с исследуемая погрешность становится существенной относительно требований [6] к точности получения экспериментальных данных на режимах взлета, а при V < 15 м/с и на режимах посадки.

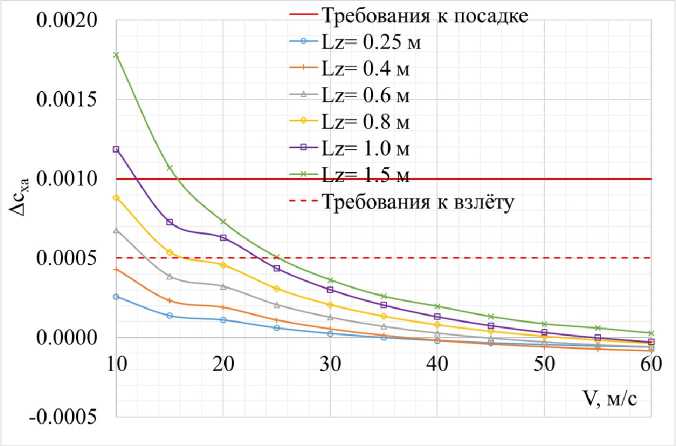
Рис. 27. Оценка минимальной систематической ошибки определения коэффициента сХа

8.    Рекомендации по использованию результатов

Полученную поправку рекомендуется использовать для увеличения точности измерений аэродинамических характеристик моделей малоразмерных ЛА (с характерной площадью значительно меньшей 0.8 м2) при скоростях воздушного потока V < 40 м/с на ленточной подвеске АВ-102 в АДТ Т-102 ЦАГИ. Уменьшение размеров моделей и снижение скорости воздушного потока требуют перехода к измерениям сравнительно малых аэродинамических нагрузок и создания соответствующих измерительных систем, рассчитанных на такие нагрузки. В этих условиях модели прямых крыльев с тщательно исследованными в настоящей работе их аэродинамическими характеристиками рекомендуется использовать в качестве эталонных для определения собственных АДХ ленточных подвесок новых измерительных систем.

Следует отметить, что в данной работе не исследовано дополнительное сопротивление, вызванное встроенными в распорку элементами крепления, которое может вносить существенный вклад в с_Ха распорок. Так, площадь омываемой поверхности цилиндрической державки в зависимости от базы L_x по отношению к площади омываемой поверхности распорки (рис. 28) может составлять от ~5% для распорки L_z = 1.5 м на базе L_x = 0.4 м до ~93% для распорки L_z = 0.25 м на базе L_x = 0.9 м. Учет этих факторов требует проведения дополнительных расчетных исследований более продвинутыми методами вычислительной аэродинамики.

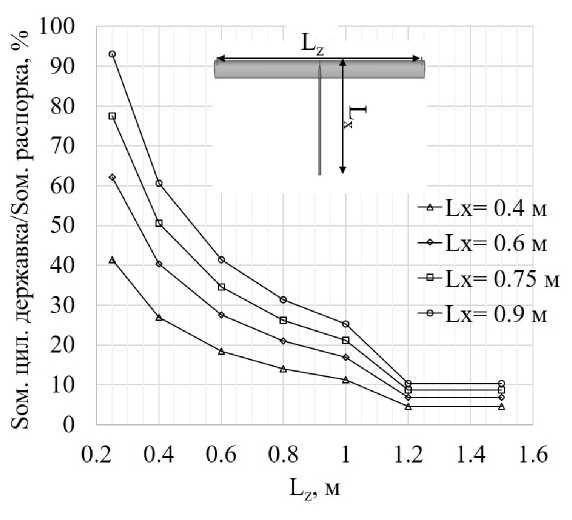
Рис. 28. Относительная площадь омываемой поверхности цилиндрической державки

9.    Заключение

Развитие малоразмерных летательных аппаратов на сегодняшний день требует расширения эксплуатационного диапазона промышленных АДТ в направлении уменьшения скорости воздушного потока и габаритных размеров испытываемых моделей. В настоящей работе исследована неисключённая систематическая погрешность определения АДХ моделей в АДТ Т-102 ЦАРИ, которая возникает при переходе к малым скоростям воздушного потока и увеличивается с уменьшением характерной площади исследуемых моделей.

Научная новизна состоит в использовании методов вычислительной аэродинамики в сочетании с автоматизированным определением геометрии моделей с помощью контрольноизмерительной машины для определения влияния скорости воздушного потока в АДТ на аэродинамическое сопротивление ленточной подвески. Исключение погрешности от этого влияния увеличивает точность получения экспериментальных АДХ моделей в АДТ.

Результаты работы рекомендуется использовать во всех дозвуковых АДТ, где проводятся испытания на ленточной подвеске.