Исследование влияния способа нагружения упругого элемента типа «беличьего колеса» на точность определения его жёсткости с помощью пакета «ANSYS»

Жильников Евгений Петрович, кандидат технических наук, профессор.

Барманов Ильдар Сергеевич, аспирант.

Бадыков Ренат Раисович, студент.

мо знать коэффициенты жёсткости опор ротора. Обычно коэффициент жёсткости определяется методами сопротивления материалов [1]. Однако наиболее точно значения коэффициента жёсткости можно получить методом конечных элементов с помощью пакета «ANSYS» [2].

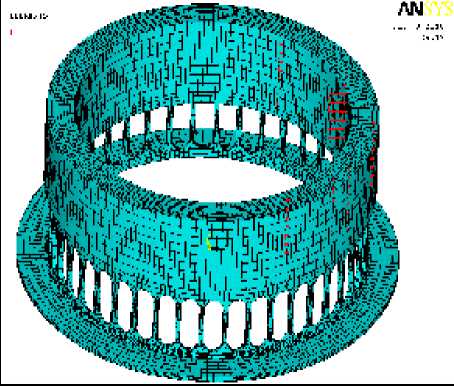
Для разбиения детали на конечные элементы необходимо выбрать размер, форму и тип конечного элемента, что влияет на точность вычислений, и задать свойства материала: модуль упругости, коэффициент Пуассона и плотность. Были выбраны два типа конечных элементов – Solid 45 и Shell 92. Разбиение объёма детали на элементы производим с помощью упорядоченной сетки. Закрепление детали осуществляем за фланец, ограничив его перемещение во всех направлениях.

Нагружение конструкции сосредоточенной силой F = 1000 Н первоначально производим в точку с внутренней стороны кольца и смотрим наибольшие перемещения в упругом элементе. Для проведения расчёта воспользуемся функцией решения (Main Menu – Solution – Solve -Current LS). Максимальные перемещения втулки составили 0,672·10^-4м (рис. 2,а).

Коэффициент жёсткости – это коэффициент пропорциональности между нагрузкой и перемещением, поэтому, поделив величину нагрузки на перемещение, получим коэффициент жёсткости упругого элемента равным 14,88·106 Н/м.

В результате наибольшие перемещения находятся в области приложения силы, где имеет место местная деформация (рис.2,б), что неудовлетворительно влияет на точность вычисления жёсткости.

Чтобы изучить влияние вида приложения нагрузки, прикладываем нагрузку той же величины, в виде распределённой по линии. При этом приложим её с внешней стороны и рассмотрим

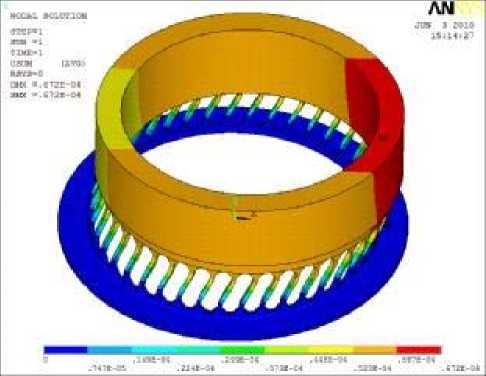
а)

Рис. 2. Деформация упругого элемента при нагружении сосредоточенной силой: а – общая деформация упругого элемента; б – местная деформация

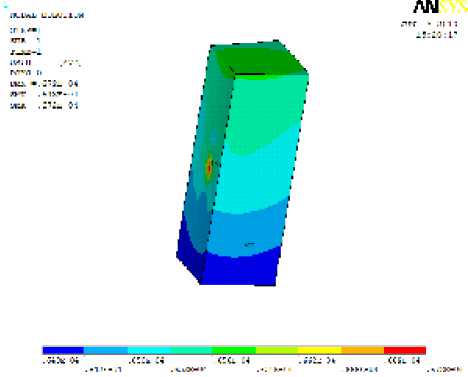
б)

перемещения посадочного кольца на диаметрально противоположной стороне. Коэффициент жесткости при этом получаем равным 19,57·106 Н/м, что на 31 % отличается от первого варианта расчёта.

Из рис. 3,б видно, что на общую деформацию оказывают влияние не только перемещения ба-лочек, но и деформация самого кольца в виде овализации.

Чтобы оценить влияние овализации на жёсткость конструкции, заменим кольцо на конце упругого элемента на сплошной диск, имитируя установку подшипника качения без зазора. В этом случае коэффициент жесткости получили равным 17,6·10 6 Н/м, что на 18 % отличается от первоначального расчёта и на 10 % от второго.

Однако в реальной конструкции нагрузка будет передаваться через тела качения в рассматриваемом случае через ролики и наружное кольцо подшипника качения на втулку упругой опоры.

Поэтому увеличим толщину кольца на величину наружной обоймы подшипника качения и приложим силу, распределяя её между телами качения роликового подшипника. Распределение нагрузки между телами качения роликового подшипника можно определить в виде [3]:

z

F r = E ( F b ■ cos ^^

i = 1

где F _r – радиальная нагрузка на подшипник, F_b – нагрузка на ролик, z – число тел качения.

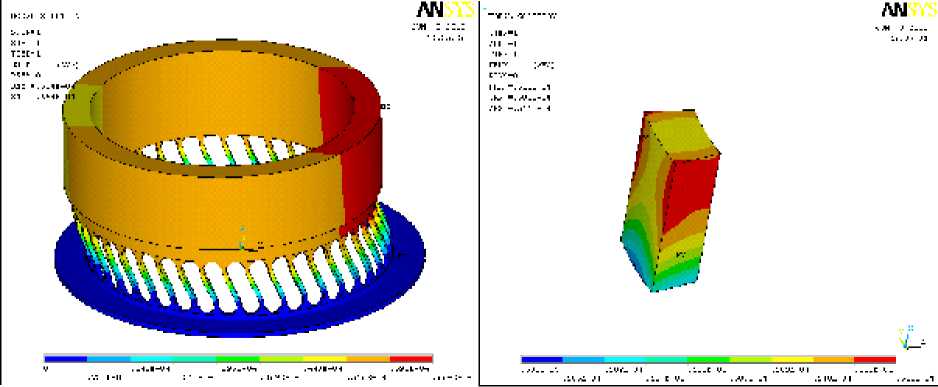
а)                                           б)

Рис. 3. Деформация упругого элемента при нагружении распределённой по линии нагрузкой: а – общая деформация упругого элемента; б – местная деформация

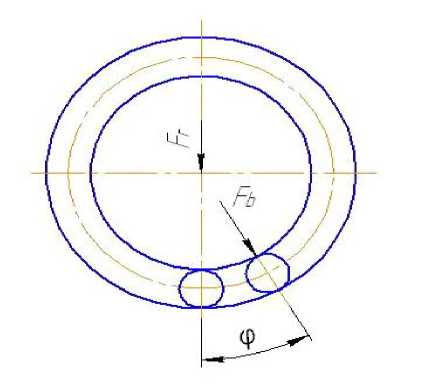
а)

Рис. 4. Нагружение упругого элемента через подшипник качения: а – распределение нагрузки между телами качения; б – приложение распределенной нагрузки

б)

а)                                                       б)

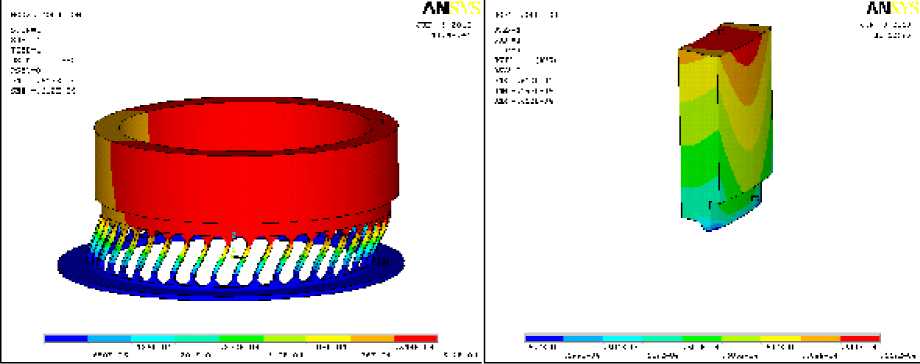
Рис. 5. Деформация упругого элемента при нагружении через подшипник: а – перемещения от распределенной нагрузки; б – перекос кольца

Значение максимальной нагрузки в контакте ролика с кольцом определяется по формуле [3]:

F _ f

b max                  ,

z где Fb max – максимальная нагрузка на ролик,

K = 4,6 – для роликовых подшипников.

Коэффициент жёсткости в этом случае равен 16,34·10 6 Н/м, что отличается на 9,8 % от первоначального значения и на 7 % от третьего варианта расчёта.

Последний способ приложения нагрузки наиболее достоверно отражает режим нагружения реальной конструкции. При этом перекос кольца невелик и составляет 1,5 мкм, а величина напряжений не превышает допустимые для материала используемого при изготовлении упругих элементов.

Исследования показали, что при расчёте жесткости деталей методом конечных элементов с помощью пакета «ANSYS» значение коэффициента жёсткости при различных способах нагружения может отличаться более чем на 30 %. В статье представлено сравнение результатов расчётов упругого элемента типа «беличьего колеса», и показано, что наиболее точные результаты расчётов можно получить при нагружении его распределённой нагрузкой через тела качения. Пакет «ANSYS» также предоставляет возможность получить результаты по напряженному состоянию в любой точке детали в соответствии с любой теорией прочности, а так же еще множество различных данных - например: форму поверхности, температурные поля и т.д., что весьма затруднительно, а порой невозможно получить с помощью методов сопротивления материалов.