Исследование влияния теплообмена на аэродинамические характеристики модели прямоугольного крыла при дозвуковых скоростях

Согласно теории влияния слабого теплообмена на сопротивление плоского тела [3], при нагревании поверхности тела, (тело отдаёт тепловую энергию в поток) его сопротивление трения уменьшается, а. при охлаждении увеличивается.

Коэффициент динамической (молекулярной) вязкости определяется по формуле Сазерленда [Sutherland]:

Д ₌ / Т \^3/2 Т^ + 110,4

. .       Т^      Т +110,4 '

Как видно, нагрев газа, приводит к увеличению динамической вязкости, так при температуре газа в набегающем потоке Тю = 255 К (-18 °C) и температуре у стенки Т = 353 К (+80 °C):    = 1, 26, охлаждение уменьшает динамическую вязкость, например, при Т = 193 К (-80 °C):     = 0, 79. Почему же при нагревании тела его сопротивление уменьшается?

Для объяснения этого факта, можно воспользоваться интегралом Крокко для стационарного течения (интеграл энергии для системы уравнений Эйлера): —       —

V х rot V = —Т •VS + VHo.

Области подвода, или стока, энергии являются источниками завихренности. Для упрощения рассматриваем адиабатический процесс: P(p^K = const, к = C_v/C_v. Тогда этот процесс будет происходить при постоянной энтропии, и V х rot V = VHo.

Охлаждение поверхности приводит к дополнительному порождению завихренности (вблизи верхней поверхности ш < 0, вблизи нижней поверхности сё > 0) и, следовательно, к индуцированию дополнительной скорости AV > 0, что обуславливает более напряженный профиль скорости в пограничном слое у стенки (рис. 1а) и больший коэффициент трения.

Нагрев поверхности также приводит к дополнительному порождению завихренности (вблизи верхней поверхности ш > 0, вблизи нижней сё < 0) и, следовательно, к индуцированию дополнительной скорости AV < 0, что обуславливает менее напряженный профиль скорости в пограничном слое у стенки (рис. 16), меньший градиент скорости и меньший коэффициент трения.

На рис. 2 приведены полученные в результате расчёта, профили скорости поперёк пограничного слоя на. задней кромке профиля П-185-12 при числе Маха, набегающего потока. М^ = 0,7 и угле атаки а = 2° в 3-х случаях: адиабатическая температура поверхности, температура всей поверхности равна -80 °C и +80 °C. Как видно, наибольшие градиенты скорости - на стенке у охлаждённой поверхности, наименьшие - у нагретой.

С целью подтверждения теоретических выводов и расчётных результатов, полученных на профиле, были проведены расчеты и эксперименты для модели прямоугольного крыла.

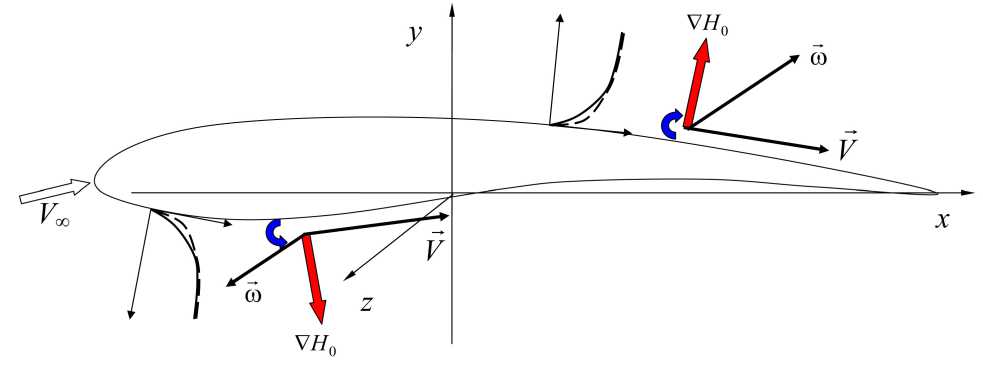
а) Охлаждение поверхности и повышение сопротивления

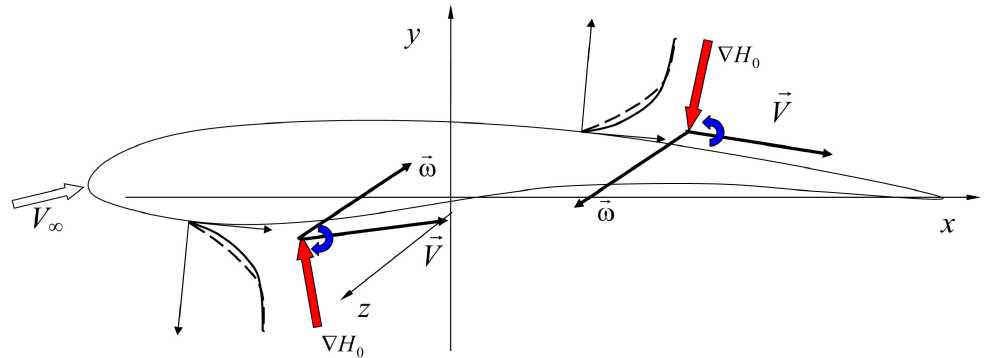
Ь) Нагрев поверхности и снижение сопротивления

Рис. 1

2.    Расчет

Расчетное исследование модели прямоугольного крыла с профилем NACA 23-021 проведено на основе трехмерной структурированной расчетной сетки 3,6 406 узлов в рамках краевой задачи для осредненных по Рейнольдсу уравнений Навье-Стокса. Задача решена с помощью компьютерного кода ANSYS CFX в стационарной постановке. Использована SST-модель турбулентности с фиксированным ламинарно-турбулентным переходом на расстоянии 5% от носка профиля при Re = 1,7406 (соответствующее число Рейнольдса перехода Re = 50). Взяты обычные граничные условия для такого рода задач [4]. Число Маха набегающего потока составляет М^ = 0,15, расчёт выполнен при углах атаки в диапазоне от 0 до 9° с шагом Aa = I⁰. Температура набегающего потока Т^ = 283 К. Модель крыла имеет хорду 0,4 м, размах 2 м, относительную толщину 21%. В предположении отсутствия скольжения потока исследовано обтекание половины крыла до плоскости симметрии. Первая ячейка расчётной сетки в пограничном слое имеет размер 10^-6 м.

Расчёты выполнены на компьютерном кластере факультета аэромеханики и летательной техники МФТИ производительностью 844 гигафлопс.

Поляры Суа (Сха), приведенные на рис. 3, демонстрируют изменения максимального аэродинамического качества под влиянием теплообмена. Нагретое крыло имеет наименьшее аэродинамическое качество, а крыло с нагретой нижней и охлажденной верхней поверхностями - наибольшее.

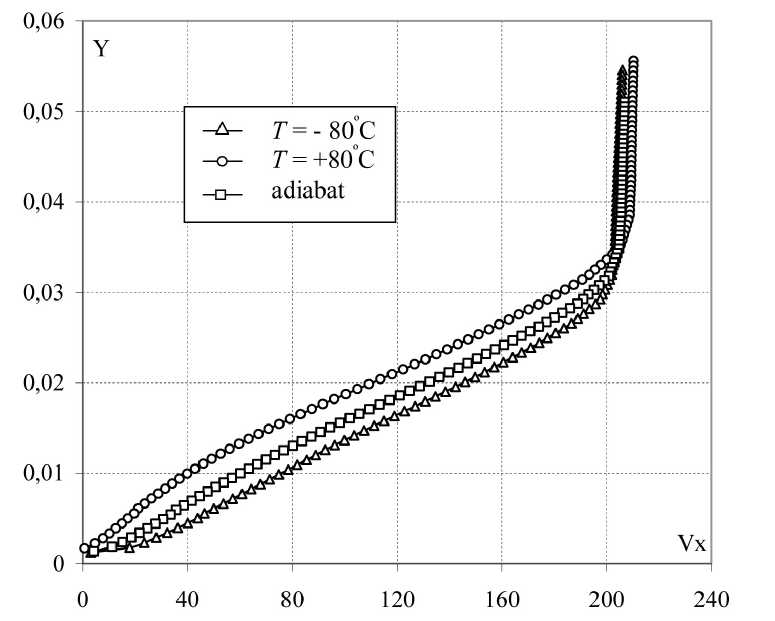
Рис. 2. Профили скорости поперёк пограничного слоя на задней кромке профиля крыла П-185-12

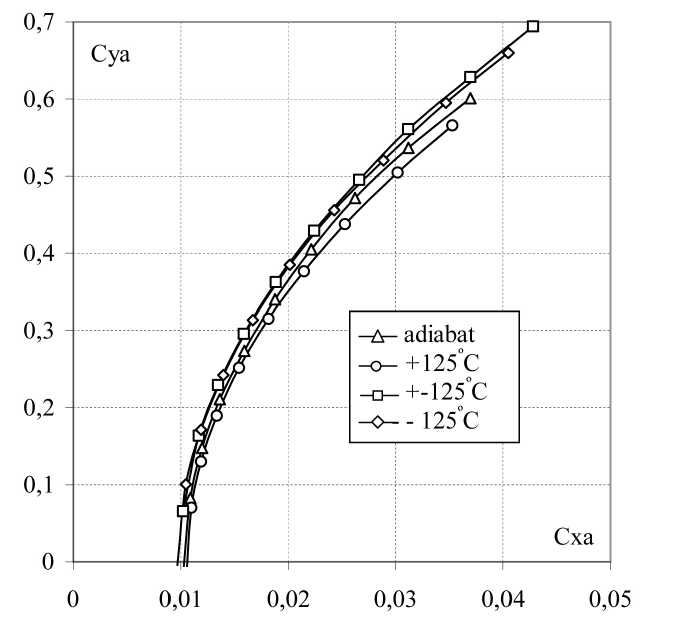
Рис. 3. Зависимости С _уа ( С_ха ) от температуры поверхности профиля

Графики аэродинамического качества ведут себя совершенно аналогично. Рис. 4 показывает, что в случае нагревания качество ухудшается, Ктах уменьшается на 4% (ДКтах = 0,7), а при одновременном нагревании и охлаждении Ктах увеличивается на 6%(ДКтах = 1).

Таким образом, результаты расчетов для крыла полностью подтверждают теорию влияния слабого теплообмена на аэродинамические характеристики профиля [2].

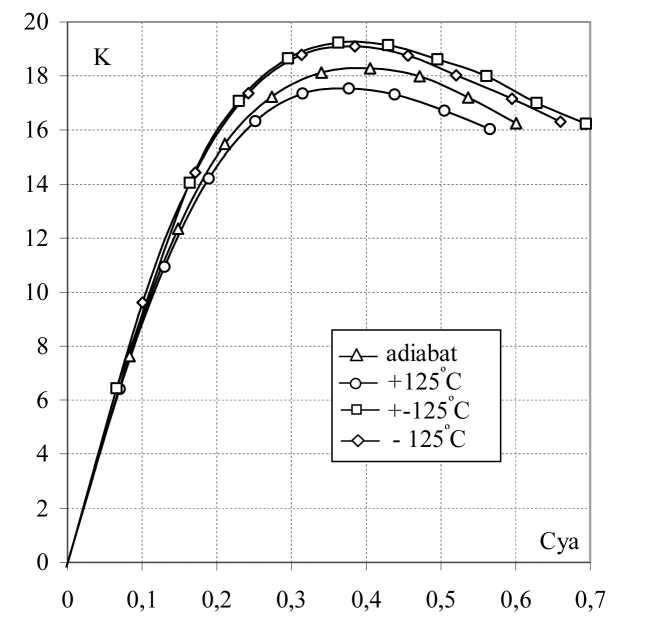
Рис. 4. Зависимости К( С_уа ) от температуры поверхности профиля

3.    Эксперимент

Весовые экспериментальные исследования влияния теплообмена модели проведены в дозвуковой аэродинамической трубе Т-102 ЦАГИ при скорости потока М^ = 0,15. Модель представляет собой цельнометаллическое прямоугольное крыло размахом А = 5 с относительной толщиной с = 21% и профилем NACA 23-021. Число Рейнольдса при испытаниях равнялось Re = 1,7406. На верхней и нижней поверхностях на расстоянии 5% от носка крыла были установлены стандартные турбулизаторы.

Модель испытывалась при начальной температуре поверхности центральной части крыла to ~ 125 °C. В процессе эксперимента модель охлаждалась потоком, и конечная температура поверхности составляла t_K0н ~ 90 °C. Температура набегающего потока при испытаниях равнялась t_BO3 ~ 10 °C.

Запланированный эксперимент с полностью охлажденной поверхностью модели с использованием «сухого льда» не удалось провести по причине большой влажности воздуха в рабочей части АДТ и моментального обледенения модели, поэтому для верификации расчёта использованы результаты эксперимента только в двух случаях: обычное и нагретое крыло.

На рис. 5-6 символ «АС» обозначает расчетные графики - пунктирные линии, а символ «ЕХ» обозначает экспериментальные результаты - сплошные линии.

Несмотря на небольшие различия между расчетом и экспериментом, согласование можно считать вполне удовлетворительным.

В соответствии с теорией на малых углах атаки из-за уменьшения сопротивления трения поляра крыла «+ 125 °C» сдвигается влево и вниз и максимальное аэродинамическое качество уменьшается (рис. 5), что получает подтверждение на рис. 6. Экспериментальные кривые ведут себя совершенно аналогично расчетным кривым. На каждом угле атаки аэродинамическое качество нагретого крыла меньше, чем у обычного крыла, а максимальное качество проигрывает на значение 0,6, что составляет 4% максимального аэродинамического качества адиабатического крыла.

4.    Выводы

Результаты расчетов качественно соответствуют результатам экспериментов, что подтверждают выводы работы [3].

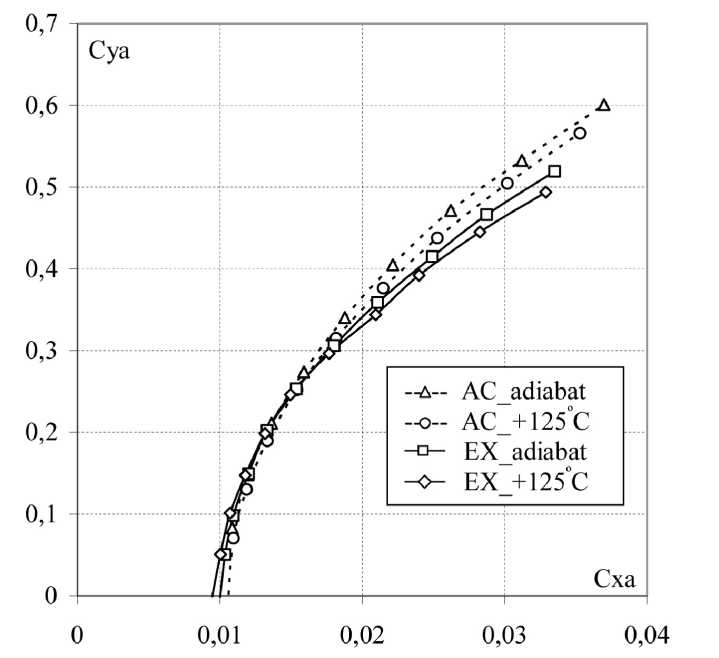
Рис. 5. Зависимости Суа (Сжа), полученные из расчета и эксперимента

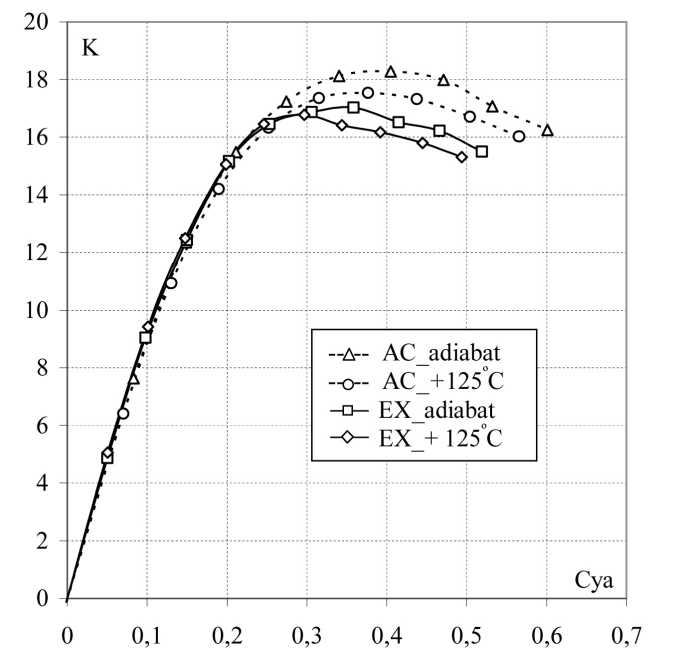
Рис. 6. Зависимости К(Суа), полученные из расчета и эксперимента

Можно утверждать, что при слабом теплообмене аэродинамические характеристики нагретого крыла хуже, аэродинамическое качество охлажденного крыла лучше, и самым лучшим вариантом организации теплообмена на поверхности крыла для улучшения его аэродинамических характеристик является одновременный нагрев нижней поверхности и охлаждение верхней.