Исследование влияния величины проводимости изоляции в месте повреждения на точность её определения косвенным методом

В настоящей работе, с учетом результатов исследований, проведенных в [1] расчеты выполняются для П-образной схемы замещения линии с отпайкой по методу узловых потенциалов (МУП).

Как и в работе [1] считается, что заданной является трехфазная цепь с симметричным источником ЭДС и симметричной нагрузкой, поэтому расчеты выполняются для схемы фазы А. Схема замещения фазы участка сети представлена на рисунке.

Расчеты выполняются с использованием данных двух цифровых моделей (ЦМ):

• -    одна ЦМ рассчитана в работе [1] для линии с отпайкой, имеющей П-образную схему замещения для симметричного режима,

• -    вторая ЦМ рассчитана в данной работе для случая ухудшения изоляции в фазе А при У_а1 = У₆₁ + 10Ке(У^) по методике, описанной в работе [1], здесь У_а1- проводимость изоляции в фазе А на первом участке;

• У _и- проводимость изоляции в фазе В на первом участке;

Y_sb- суммарная проводимость изоляции в фазе В, где Ь_ь=Ьх+Ьг+Ьз-.

• Y _b2- проводимость изоляции в фазе В на втором участке;

• У    ₆₃ - проводимость изоляции в фазе В на от-паечном участке.

Действительные значения измеряемых величин, полученные в цифровых моделях, используются при моделировании измерений напряжений и токов приборами класса 0,1 для 100 циклов изме-

П-образная схема замещения фазы участка сети

рений. Расчеты выполняются по методу узловых потенциалов для П-образной схемы замещения (см. рисунок) по трем вариантам уравнений цепи.

Вариант 1

В расчетах принимаем U_X=U_X;

U2=U2- е^^ ;U3=U3- eJ3mM, где ц/ = у2 + ЛУз = 3Десь V2 ~ начальная фаза напряжения U2 в конце второго участка; \р3 - начальная фаза напряжения U3 в конце отпаечной линии.

Так же, как и в работе [2] вводятся обозначения: I_X=I_V е"^№ ; 1'₂=1₂- е"^т ; /₃ = /₃ • е^-^³.

Данными цифровых моделей являются: Г,^,?и, v = V2 + М> где У - проводимость основной линии; ^ - проводимость отпаечной линии; т - коэффициент распределения проводимости или доля проводимости первого участка в основной линии.

Расчеты ведем по данным двух цифровых моделей отдельно.

Запишем уравнения по методу узловых потенциалов:

Ф1 =U_X;

Фг =й₂;

Фз = ^3S

Фо ' 5ю — Ф1' 1Ь1 — Фа ' 5)2 _ Фз ‘ 5>з = 0’

Z2           2          '     V 2 2’

.^(v) .6+j;

Z3          3          2

Из второго уравнения выразим напряжение в месте присоединения отпайки

.         m-YZx -

UO=UX.^^=^-IX-ZX и подставим в остальные уравнения системы. В результате получим:

-U L_u ^    ejW ■ —

21            22             2з

uxU^Mivz

и,. Ц-^iZi U-Z.

+ Ь

где 5п - ;      5)2 - —;      5>з -   ;

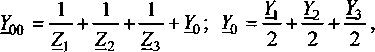
здесь Z_x - сопротивление первого участка

линии; Z2 - сопротивление второго участка линии; Z3 - сопротивление отпаечной линии.

Сделав замены согласно формул

—+ —+— = g ;    5 = 5 ⁺ ^ = получим.

21 2г 2з

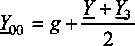
С учетом приведенных выше обозначений уравнения по методу узловых потенциалов запишутся в виде:

U^g^-u'-U^l

= 0;

2з

Z, 1 2      1

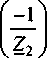
,еУКе(у) =0.

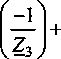
. gyJm(w) _ у

и выполним расчет данных уравнений в программе MathCAD.

Вариант 2

К полученным выше уравнениям дабавим дополнительные уравнения для токов Ло > Аг >  Аз ^в месте присоединения отпайки, записанные по законам Кирхгофа и Ома для трех участков линии. В результате получим уравнения:

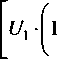
т-У-гЛ

2 J

-5-21

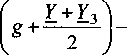
__и А__и е^) —__и e^j3mW ■ — = 0;

U_x J 1 +

m-YZ

-А -21

-1

2г >

и2 - — +

2з

+ А ,еУК=бР)=0;

U3-

-1

Z

— +^ +А -е»)=0; (2з 2J ³]

■ m-Y     (_

L---- U_x ■ 2 +

1      2           (

m-YZ

5 ■ 2i Ло - 0s

у ДХ-^-Y '2 ⁺    „

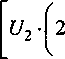
2 J 2

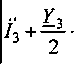
( Y -7 \   ,

U₃- 2 + ^=2- +/₃-Z₃

-/03 -0.

и выполним расчет данных уравнений в программе MathCAD.

Вариант 3

К полученным выше по 1-му варианту уравнениям введем дополнительные уравнения для напряжения [/0 в месте присоединения отпайки, записанные по законам Кирхгофа и Ома для трех участков линии. В результате получим уравнения:

^'Г ^'2     -¹

• g+---- -ц —

I 2 ) Z,

-U. •      — - U, ■ e^yJm(v) ■ — = 0:

^3

UvU + ^^M-ix-Zx

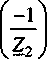
_eVRe(v) ₌ q.

UxW^Vix-Zx

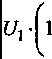
m Y Zx) ■

2    )

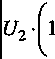
(l-m)YZ2

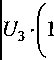
Гз^з)

2 J

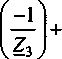
eyJm(v) = 0;

-^o=O;

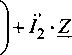
-Uo=O;

+ /3 Z3

-uo=o.

Все три варианта уравнений с данными двух цифровых моделей (симметричной и с ухудшением изоляции) решаются методом минимизации среднеквадратичной погрешности в программе MathCAD.

Результаты расчета погрешности определения суммарной проводимости изоляции по двум цифровым моделям для трех вариантов уравнений цепи приведены в табл. 1 и 2.

Из табл. 1 видно, что для симметричной цепи 3-й вариант с дополнительными уравнениями по напряжению дает большую погрешность в определении параметров изоляции. Это связано с тем, что напряжение в начале линии Ц и в месте присоединения отпайки U_o мало отличаются друг от друга, так как падение напряжения на первом участке с сопротивлением Z, незначительно. Дополнительные уравнения по напряжению накладывают в расчеты дополнительную погрешность, в результате чего увеличивается общая погрешность в определении параметров изоляции. Поэтому 3-й вариант расчетов с дополнительными уравнениями по напряжению для симметричной цепи при определении проводимости изоляции и места повреждения в дальнейших расчетах не рассматривается.

Данные погрешности из табл. 2 получились из-за того, что не учтено изменение коэффициента распределения проводимости т . В случае ухудшения изоляции коэффициент т не соответствует распределению проводимости по участкам сети. Поэтому необходимо выполнить перерасчет коэффициента распределения проводимости т по предполагаемым гипотезам повреждения участков сети.

В расчетах используем средние значения проводимостей, полученные при определении параметров по всем трем вариантам уравнений:

• -    в случае ухудшения изоляции

у _ ^япах ^^.ттш । ■ ®s max ®s min _ СОСД

• -    ₂ J ₂ — ср д-няя суммарная проводимость поврежденной фазы А;

Таблица 1

Погрешности определения суммарной проводимости изоляции (для симметричной ЦМ)

Варианты уравнений	Gs max, %	Gs min, %	Bs max, %	Bs min, %
1	33,293	-47,492	49,587	-45,116
2	13,351	-22,356	10,659	-24,089
3	67,358	-116,513	215,448	-70,421

Таблица 2

Погрешности определения суммарной проводимости изоляции (для ЦМ с ухудшением изоляции)

Варианты уравнений	Gs max, %	Gs min, %	Bs max, %	Bs min, %
1	7,770	4,338	348,277	209,274
2	44,067	28,542	32,795	17,588
3	46,266	6,990	123,921	-68,617

• -    в симметричном режиме

тл ^max ~*"^тт , ,:^лтах                _

Lsb -      2     " +       ~       - сред няя суммарная проводимость фазы В;

у₌ ^тах +^т^₊ ^^max+^min _ _{средняя} проводимость главной линии;

v ^»тах "*"^$min , • Д$max +-^тт

Ь = -----2----- ^J-----2----- ~ ^{Р Д}"

няя проводимость отпаечной линии;

АУ = Уга-У,6 - величина ухудшения суммарной проводимости изоляции.

Гипотеза 1

Предполагается ухудшение изоляции в фазе А на первом (головном) участке (1-0). Тогда для второго участка без повреждения величина проводимости У₂ =(1->и) У определяется по заданному коэффициенту распределения проводимости т .

На первом участке проводимость У, определяем с учетом ухудшения изоляции как ¥_х = У-У₂, где проводимость У определяется с учетом ухудшения изоляции как У = У⁷ + АУ, здесь У⁷ - среднее значение проводимости главной линии, рассчитанное выше. После этого выполняем перерасчет коэффициента распределения проводимости т —.

Далее выполняются расчеты по всем трем вариантам уравнений в программе MathCAD.

Гипотеза 2

Предполагается ухудшение изоляции в фазе А на втором участке (0-2). Тогда для первого участка без повреждения величина проводимости У] = т-¥ определяется по заданному коэффициенту распределения проводимости т.

На втором участке проводимость У2 определяем с учетом ухудшения изоляции как У2 = ¥-¥1, где проводимость У определяется с учетом ухудшения изоляции аналогично гипотезе 1 как У = У7 + АУ . Аналогично выполняем перерас чет коэффициента распределения проводимости

Далее выполняются расчеты по всем трем вариантам уравнений в программе MathCAD.

Гипотеза 3

Предполагается ухудшение изоляции в фазе А на третьем участке (0-3). Тогда для третьего участка величина проводимости Уз = Уз + АУ, где Уз - среднее значение проводимости отпаечной линии, рассчитанное выше.

Коэффициент распределения проводимости т сохранился.

Далее аналогично выполняются расчеты по всем трем вариантам уравнений методом минимизации среднеквадратичной погрешности в программе MathCAD.

Результаты расчета погрешности определения суммарной проводимости изоляции по трем гипотезам для трех вариантов уравнений цепи приведены в табл. 3.

Проанализируем результаты расчетов, представленные в табл. 3.

Вполне допустимые результаты расчетов по 1 варианту уравнений наблюдаются по гипотезе 1. Результаты расчета погрешностей по 2 и 3 гипотезам по некоторым суммарным проводимостям в сотни, тысячи раз превышают показатели по 1 гипотезе.

Результаты расчетов 2 варианта с дополнительными уравнениями по току дают хороший результат также по 1 гипотезе. Погрешности расчетов по 2 и 3 гипотезам превышают в десятки, сотни раз показатели суммарной проводимости по 1 гипотезе.

Результаты расчетов 3 варианта с дополнительными уравнениями по напряжению дают также лучший результат по 1 гипотезе по сравнению с гипотезами 2 и 3. Однако даже по 1 гипотезе наблюдается большая погрешность. Причина такой большой погрешности результатов расчета была отмечена выше, поэтому 3 вариант с дополнительными уравнениями по напряжению для случая ухудшения изоляции, также как и для симметрич-

Погрешности определения суммарной проводимости изоляции

Таблица 3

Варианты Гипотезы Gs max, % Gs min, % Bs max, % Bs min, % 1 1 4,684 -2,034 79,292 -30,833 2 13,904 -1309,841 5023,801 -104,958 3 7,770 4,338 348,277 209,274 2 1 2,550 -2,994 10,126 -18,781 2 -95,235 -95,680 -38,845 -43,600 3 -94,413 -114,012 46,750 -48,379 3 1 7,790 -13,072 128,889 -77,515 2 107,723 45,980 238,842 146,164 3 41,527 -235,192 1120,569 -70,380 ного режима, в дальнейших расчетах по определению проводимости изоляции и места повреждения не рассматривается.

Таким образом, анализ данных табл. 3 дает положительный результат по 1 гипотезе, что подтверждает наличие повреждения изоляции на первом участке цепи. Гипотезы 2 и 3 в дальнейших расчетах не рассматриваются.

Анализ полученных значений погрешностей определения суммарной проводимости изоляции, приведенных в табл. 3, показывает, что лучшими являются результаты по 2 варианту с дополнительными уравнениями по току. Это связано со значительным изменением токов в цепи за счет довольно существенных токов утечки на землю. Поэтому дополнительные уравнения по току дают большую точность в расчетах, тем самым, уменьшая величину погрешности определения проводимости изоляции.

На следующем этапе для гипотезы 1 уже для оставшихся двух вариантов уравнений выполняется уточнение параметров изоляции линии с отпайкой и перерасчет правильной гипотезы по не скольким приближениям. Расчеты уравнений выполняются в программе MathCAD.

Для 1 варианта уравнений выполнено шесть приближений, результаты приведены в табл. 4.

Результаты, приведенные в табл. 4 показывают, что 4-гб приближения практически не отличаются от 3-го приближения. Кроме того, погрешности расчетов меняются по случайному закону, и разница в погрешностях расчета определяется случайной погрешностью измерительных приборов, поэтому в дальнейших расчетах ограничиваемся тремя приближениями. Для проводимости третьего участка (отпаечной линии) получаем значения не совпадающие с действительными. Это связано с тем, что проводимость отпаечной линии на порядок меньше проводимости поврежденного участка.

Для 2 варианта с дополнительными уравнениями по току, с учетом изложенного выше, рассчитано три приближения, результаты приведены в табл. 5.

По данным табл. 5 можно отметить, что погрешности расчетов по определению проводимости изоляции в сравнении с данными табл. 4 уменьша-

Таблица4

Уточнение погрешности определения проводимости изоляции и величины ухудшения суммарной проводимости по участкам сети по 1 варианту уравнений для гипотезы 1

Приближения	1	2	3
АУ	0,00367+0,000158i	0,00360+0,0000236i	0,00359+0,00000555i
G шах, %	55,784	59,781	60,366
G min, %	-57,756	-57,172	-57,088
В шах, %	420,685	452,927	457,654
В min, %	-427,320	-422,740	-422,080
G3 max, %	1995,481	1975,698	1972,848
G3 min, %	-1966,970	-2111,870	-2133,120
ВЗ max, %	1078,294	1067,038	1065,417
ВЗ min, %	-1031,893	-1109,368	1065,417
Gs max, %	4,463	4,4292	4,424
Gs min, %	-5,511	-6,0261	-6,102
Bs max, %	74,551	73,852	73,752
Bs min, %	-63,507	-67,837	-68,468
Приближения	4	5	6
АУ	0,00359+0,00000292i	0,00359+0,00000253i	0,00359+0,00000247i
G max, %	60,453	60,466	60,467
G min, %	-57,076	-57,074	-57,074
В max, %	458,351	458,454	458,469
В min, %	-421,983	-421,969	-421,967
G3 max, %	1972,429	1972,368	1972,359
G3 min, %	-2136,253	-2136,715	-2136,783
B3 max, %	1065,179	1065,144	1065,139
B3 min, %	-1122,387	-1122,634	-1122,671
Gsmax,%	4,423	4,423	4,423
Gs min, %	-6,113	-6,115	-6,115
Bs max, %	73,737	73,735	73,734
Bs min, %	-68,561	-68,575	-68,577

■                                                    Таблица 5

Уточнение погрешности определения проводимости изоляции и величины ухудшения суммарной проводимости по участкам сети по 2 варианту уравнений для гипотезы 1

Приближения	1	2	3
АУ	0,0036+0,0000171 i	0,00356+0,0000188i	0,0036+0,0000395i
G max, %	5,073	5,115	5,113
G min, %	-2,987	-2,945	-2,957
В max, %	81,605	82,194	81,590
В min, %	-59,797	-59,307	-59,893
G3 max, %	113,757	112,696	113,530
G3 min, %	-184,572	-185,949	-185,107
B3 max, %	132,125	131,100	132,040
B3 min, %	-184,012	-185,169	-184,322
Gs max, %	0,872	0,833	0,942
Gs min, %	-3,460	-1,567	-1,253
Bs max, %	10,076	15,801	12,972
Bs min, %	-18,2786	-18,247	-18,497

Таблица 6

Погрешности определения проводимости изоляции и величина ухудшения суммарной проводимости по участкам сети по результатам проверки правильности программы

Варианты 1 2 АУ 0,00367+0,000158i 0,00360+0,000017 li G max, % 55,527 4,575 G min, % -53,933 -3,467 В max, % 418,072 76,049 В min, % -398,001 -64,205 G3 max, % 1863,986 124,318 G3 min, % -1960,548 -170,239 B3 max, % 1003,509 142,020 B3 min, % -1028,482 -172,274 Gs max,% 4,185 1,024 Gs min, % -5,565 -1,056 Bs max, % 69,168 8,954 Bs min, % -64,112 -11,403 ются, особенно для отпаечной линии. Порядок величины погрешности определяется правильно, но сами значения для отпаечной линии не соответствуют действительным по причине, указанной выше. Так как результаты данных табл. 5 практически близки друг другу, то достаточно уточнения по 1-му приближению, и дальнейшее уточнение расчетов не требуются; то же самое можно сказать о результатах расчета приведенных в табл. 4.

Поэтому для гипотезы 1 выполняется проверка правильности программы для двух вариантов уравнений цепи по первому приближению, с перерасчетом коэффициента распределения проводимости т по данным цифровой модели с ухудшением изоляции

^1+^2’ где Уа1 - проводимость на первом участке с ухудшением изоляции, Уа2 - проводимость на втором участке.

Расчеты уравнений выполняются в программе MathCAD. Результаты проверки правильности программы по расчету погрешности определения проводимости изоляции по участкам сети приведены в табл. 6.

Данные табл. 6 близки к результатам первого приближения по данным табл. 4 и 5. Это подтверждает правильность программы по расчету погрешности определения проводимости изоляции по участкам сети и дает возможность определения места повреждения участка линии, в зависимости от величины проводимости изоляции в месте повреждения.