Исследование внутривидовой конкуренции при разных схемах посадки деревьев

Институт комплексного анализа региональных проблем ДВО РАН, ул. Шолом-Алейхема 4, г. Биробиджан, 679016, e-mail: ,

При создании искусственных лесонасаждений необходимо увеличивать запас выращиваемой древесины. Одним из способов повысить продуктивность насаждений является минимизация внутривидовой конкуренции, которая усиливается в процессе роста древостоя и приводит к возникновению процессов самоизреживания. Показано, что процессы самоизреживания древостоя зависят как от начальной густоты насаждений, так и от взаимного расположения деревьев на участке, что в итоге определяет величину запаса древесины с заданными качественными характеристиками [2]. Чем выше начальная густота насаждений, тем раньше возникает процесс изреживания в силу того, что раньше происходит смыкание крон, усиливая напряженность конкурентных отношений. При этом одинаковое число деревьев можно расположить разными способами, что также влияет на распределение ресурсов и, соответственно, отмирание деревьев в результате конкуренции.

В связи с этим возникают задачи, направленные на исследование внутривидовой конку- ренции в зависимости от взаимного расположения деревьев и начальной густоты древостоя.

Для исследования процессов изреживания в зависимости от взаимного расположения деревьев использовали имитационную модель динамики древесных сообществ, в которой учитывается пространственное расположение каждого дерева, что позволяет легко имитировать различные схемы посадки [3].

Моделирование роста древостоя проводили для шахматной и прямоугольной схем посадки. Проведенные вычислительные эксперименты показали, что в случае одинаковой начальной густоты насаждений процесс самоизреживания древостоя при прямоугольной схеме посадки возникает раньше, чем при шахматной схеме посадки (рис. 1а). Таким образом, напряженность конкурентных отношений в первом случае оказывается выше. При ежегодном изъятии 1,5% деревьев в течение 60 лет процессы изреживания в обоих случаях не возникают (рис. 1б).

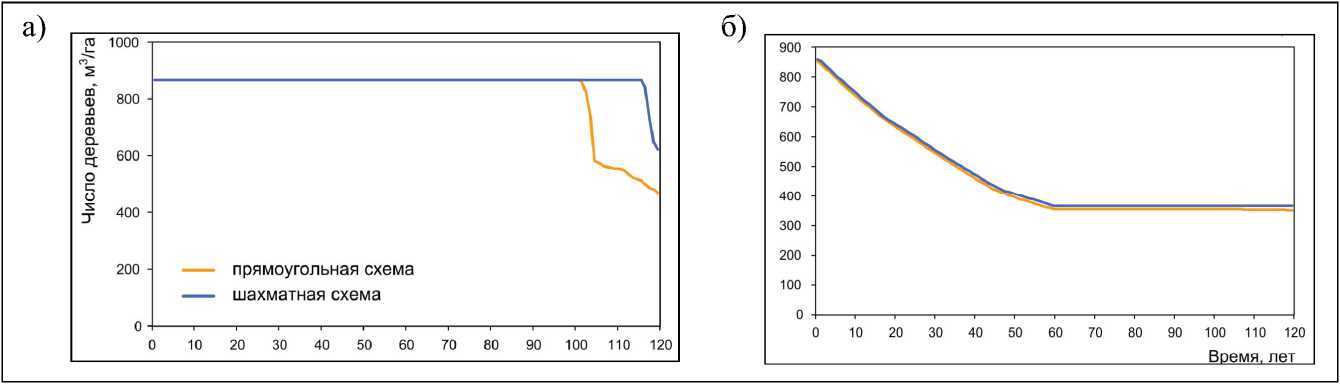
Рис. 1. Динамика численности древостоя для прямоугольной и шахматной схем посадки: а) без изъятия; б) при ежегодном изъятии деревьев в течение 60 лет

Fig 1. Dynamics of tree stand population for rectangular and checkerboard planting schemes: a) without removal; b) with annual removal of trees for 60 years

Далее производили оценку напряженности конкурентных отношений при таких схемах посадки. Деревья разделили на две группы по размеру диаметра ствола: «мелкие» и «крупные». В этом случае напряженность конкурентных отношений должна зависеть от расстояния между «мелкими» и «крупными» деревьями, а также от количества «крупных» деревьев вокруг «мелкого».

Для оценки частоты встречаемости «мелких» и «крупных» деревьев на определенном расстоянии друг от друга использовали кросс-корреляционную функцию [1]. Значения этой функции g .j (r) определяются с помощью среднего числа пар точек типа i и j, расположенных на расстоянии, меньшем r . Здесь i , j соответствуют «мелким» и «крупным» деревьям.

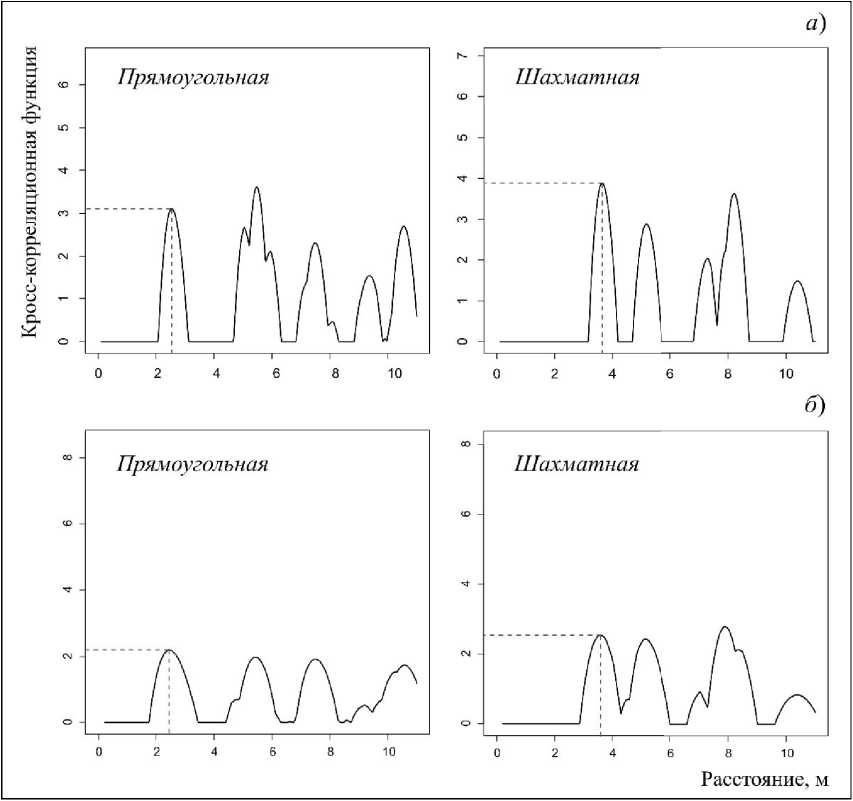
Рис. 2. Значения кросс-корреляционной функции для шахматной и прямоугольной схем посадки: а) без воздействия внешних факторов; б) при ежегодном изъятии деревьев в течение 60 лет

Fig. 2. Values of the cross-correlation function for a checkerboard and rectangular planting pattern: a) without the influence of external factors; b) with annual removal of trees for 60 years

Значения функции g_ij(r) показали, что для прямоугольной схемы посадки высокая частота встречаемости «мелких» и «крупных» деревьев наблюдается на расстоянии r = 2.2 м, для шахматной схемы посадки r = 3.8 м (рис. 2 а). При ежегодном изъятии 1,5% деревьев в течение 60 лет значения функции существенно снижаются (рис. 2 б). Таким образом, значение этой функции при анализе пространственных данных может служить пороговой величиной, ниже которой процессы из-реживания не происходят.