ИССЛЕДОВАНИЕ ВОЗМОЖНОСТЕЙ СОЗДАНИЯ СИСТЕМ СВЯЗИ ПОВЫШЕННОЙ ЭФФЕКТИВНОСТИ С ИСПОЛЬЗОВАНИЕМ НЕКЛАССИЧЕСКИХ ПОДХОДОВ

При проведении анализа состояния современных систем радиосвязи периодически встречаются работы, посвященные построению комплексов радиосвязи с использованием достаточно оригинальных подходов. Например, к подобным относятся работы [1; 2], в которых рассматриваются системы связи с обеспечением формирования импульсного сигнала с изменяющейся по заданному закону частотой вращения вектора поляризации. Утверждается, что применение подхода управления вектором поляризации электромагнитной волны позволит значительным образом улучшить характеристики всей системы в целом. В частности, такой подход позволяет:

– за счет эффекта самофокусировки поля существенно уменьшить габариты антенных устройств и организовать управление шириной диаграммы направленности в реальном масштабе времени. Кроме того, это позволит организовать канал активной обратной связи;

– на порядки повысить пропускную способность канала (скорость передачи информации);

– организовать электронное сканирование, что позволит обеспечить получение значительного количества пространственно-разнесенных каналов связи, т.е. работать одним наземным ком- плектом со значительным количеством абонентов в реальном масштабе времени при требуемой пропускной способности каждого канала;

– существенно повысить помехозащищенность линии и понизить вероятность ошибочного приема на бит информации;

– снизить зависимость качества передачи информации от характера движения абонента, погодных условий, рельефа местности;

– построение линии радиосвязи в указанном диапазоне позволит ограничиться твердотельной элементной базой и снизить себестоимость линии, особенно с учетом ее пространственной многоканальности.

Вышеуказанные преимущества таких систем связи обеспечиваются новым подходом к формированию пространственно-временной структуры электромагнитного поля (ЭМП) посредством управления его поляризационными характеристиками и возможности его применения для решения различных задач построения систем связи. Утверждается, что предложенный способ управления пространственно-временной структурой ЭМП позволит решать ряд актуальных задач организации многоканальной сверхскоростной высокозащищенной радиосвязи и систем передачи данных в воздушной, водной и земной приповерхностной средах.

Системы связи с использованием различных видов поляризации электромагнитных волн

Для предлагаемого способа необходимо соблюдение ряда условий:

– поляризация должна быть круговой;

– частота вращения вектора поляризации не должна зависеть от несущей, которая может оставаться неизменной;

– управление пространственно-временной структурой ЭМП реализуется путем перестройки частоты вращения вектора поляризации.

Утверждается, что в этом случае наряду с поперечной формируется также и продольная составляющая электрического поля. Вектор напряженности электрического поля наклоняется в сторону направления распространения волны. При этом угол наклона определяется скоростью перестройки и возрастает с ее увеличением. Фазовый фронт волны из плоского трансформируется в гиперболический, что приводит к сужению диаграммы направленности. Степень сужения диаграммы направленности увеличивается с ростом оптической плотности среды распространения. Авторы предлагают генерировать сигналы с вектором поляризации, который вращается с частотой, отличающейся от несущей, применяя метод балансно-амплитудной модуляции сигналов в неподвижных ортогональных излучателях. Согласно их утверждениям, электрическая составляющая электромагнитного поля, создаваемого описанным способом, являет- ся результатом суперпозиции двух ортогональных пространственных составляющих Ex и Ey :

Ex = cos ( Q t ) cos ( w t ) , Ey = sin ( Q t ) cos ( w t ) ,

где ω – несущая частота;

^Q - частота вращения (ротации) вектора поляризации электромагнитной волны круговой поляризации. При этом положим условие Ω < ω.

Преобразуем (1) с помощью известных формул для синуса и косинуса суммы и разности аргументов, получим (2):

Как следует из (2) при таком возбуждении диполей их поле излучения представляет собой суперпозицию двух волн с частотами w + Q и w- Q с левой и правой круговыми поляризациями соответственно, а не волну с вектором поляризации, вращающимся с частотой, независящей от частоты несущей.

Для исследования прохождения электромагнитных волн линейной и круговой поляризаций через слоистую неоднородную среду был разработан ряд микрополосковых антенн линейной поляризации, а также ряд микрополосковых антенн круговой поляризации. Неоднородная среда представляет собой 3 слоя материала с различными электрическими характеристиками. Схема эксперимента представлена на рисунке 1.

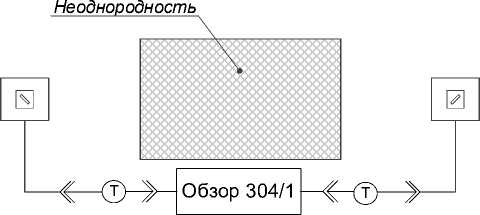
Рисунок 1. Схема измерения коэффициента прохождения

Были определены зависимости коэффициента прохождения (параметр S ₂₁) через неоднородную среду при зеркальном расположении антенн линейной и круговой поляризаций, а также зависимость коэффициента прохождения через неоднородную среду при ортогональном расположении антенны линейной поляризации (одна антенна повернута на 90º вокруг главной оси).

В результате эксперимента установлено, что коэффициент прохождения таких волн практически не отличается от коэффициента прохождения линейно поляризованных волн в условиях аналогичной среды.

Результаты проведенных испытаний подтвердили высокий уровень затухания радиоволн при прохождении через среды.

В результате эксперимента также установлено, что существенной зависимости затухания от вида поляризации не установлено.

Возможность организации радиосвязи в УВЧ – СВЧ диапазонах в условиях неоднородной среды за счет управления видом поляризации не подтвердилась.

cos ( Q + w ) t + cos ( Q-w ) t 1    ,      .    1    ,      \

Ex = cos (Qt) cos (w t) =------------------— = —cos (® + Q) t + —cos (®-Q) t,sin (Q + w) t + sin (Q-w) t 1              1Ey = sin (Qt) cos (w t) =------------------— = —sin (w + Q) t - —sin (w-Q) t =

= cos

(® + Q) t- 2

1      /            n

+ —cos ( w-Q ) t + — ,

Следует также отметить, что в работе [3] изложены материалы в области исследования технических решений систем связи с использованием различных поляризационных составляющих электромагнитных волн, которые, в свою очередь, не противоречат полученным результатам.

Возможности создания систем связи с использованием продольных волн

Проанализируем также возможности создания систем связи с использованием продольных волн [4–6], которым посвящено достаточно большое количество работ [7–18].

Для описания распространения электромагнитных волн в вакууме и их взаимодействия с материальными средами зачастую достаточно классической макроскопической электродинамики, основанной на уравнениях Максвелла и элементарных материальных соотношениях. В этом подходе среда характеризуется ключевыми параметрами, такими как диэлектрическая и магнитная проницаемость, а также электропроводность.

Современная электродинамика расширяет этот классический взгляд, вводя концепцию продольных волн через специальные материальные уравнения для сред с пространственной дисперсией [4; 5]. Параллельно развивается общая теория волн в электромагнитно-упругих средах [6]. В ряде исследований [7–9] предложены обобщенные уравнения электродинамики, включающие дополнительные потенциалы для описания продольных электромагнитных волн. Однако эти модели остаются гипотетическими и требуют экспериментального подтверждения.

За последние 25 лет появилось несколько экспериментальных работ [10–21], в которых сообщается о возбуждении продольных электромагнитных волн (TEM), обладающих свойствами, существенно отличающимися от традиционных электромагнитных волн. Однако основным недостатком таких исследований является отсутствие или недостаточная трактовка полученных результатов с позиции классической электродинамической теории, базирующейся на уравнениях Максвелла и простых материальных соотношениях.

Более подробный анализ упомянутых работ по продольным электромагнитным волнам с позиций классической электромагнитной теории приведен в [22].

Например, в работе [14] приведены результаты эксперимента, которые показывают наличие продольной компоненты электромагнитной волны, но не сами продольные электромагнитные волны, как показано в работе.

Анализ возможностей передачи радиосигналов в открытом пространстве с использованием продольных электромагнитных волн

Проанализируем возможности передачи сигналов с точки зрения классической электродинамики.

Запишем уравнения Максвелла в дифференциальной форме [23]:

rot H = jros'aE + je, rot II = - j гоц aH - jm.

Здесь E - вектор комплексной амплитуды напряженности электрического поля, В/м;

H - вектор комплексной амплитуды напряженности магнитного поля, А/м;

^s a = ^s a

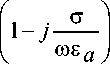
комплексная диэлек-

трическая проницаемость среды;

s _a - диэлектрическая проницаемость среды, Ф/м для вакуума;

^s 0 =

- 9

36 п

, Ф/м;

Ц _a - магнитная проницаемость среды, Гн/м для вакуума;

.      -7

ц 0 = 4 л- 10 , Гн/м;

ст - удельная объемная проводимость среды, См/м;

j ^e – вектор комплексной амплитуды объемной плотности электрического тока, А/м^2;

j ^m – вектор комплексной амплитуды объемной плотности стороннего магнитного тока, В/м^2;

Сторонний магнитный ток является фиктивной величиной, поскольку магнитных зарядов в природе не существует. Однако введение этого понятия позволяет упростить целый ряд расчетов.

Для решения уравнений Максвелла обычно вводят два вспомогательных векторных поля:

1 e векторный потенциал электрических токов A и векторный потенциал магнитных токов A m . Векторы электромагнитного поля Е и H определяются через эти вспомогательные векторы следующим образом:

Е = - i юц _a A ^e А --graddiv A ^e - rot A m ,

i ®e'^

H = — i ®e'aA m А ---—graddiv A m + rot A ^e .

i юц ^

При подстановке (4) в (3) получаются следу- ющие векторные неоднородные уравнения Гельмгольца относительно векторных потенциалов:

^      ^     ^

A A e + k ² A e =- j e ,

^      ^     ^

AAm + k2 Am =-jm, где:

A A = grad div A - rot rot A , k = ®4 ^e' a И a .

Таким образом, интегрирование уравнений Максвелла сводится к нахождению решений векторных неоднородных уравнений (5).

При расчете ЭМ полей излучающих систем с известным распределением возбуждающих электрических и магнитных токов j^{e ,} m ( x'yy ', z ') обычно используется ряд стандартных упрощающих предположений. Первое из них состоит в том, что излучающая система исследуемой антенны располагается в неограниченном однородном пространстве. В этом случае векторный потенциал в произвольной точке наблюдения P ( x , y , z ) определяется выражением:

A e , m ( x , y , z ) = -1- J Г , m ( x ‘ , У ‘ , z ') exp ^ — ikr ) dV , (6) 4 n r

V где r = ^( x - x') 2 +(y - y') 2 +(z - z') 2 - расстояние между точками наблюдения P (x, y, z) и интегрирования Q(x',y', z');

V – объем, занимаемый токами излучающей системы.

Выражение (6) представляет собой строгое решение векторных неоднородных уравнений Гельмгольца (5). Оно является единственным, поскольку удовлетворяет условию на бесконечности и имеет всюду конечную величину. Последующая подстановка (6) в (4) позволяет определить векторы полей E и H i для любой точки пространства.

В теории антенн приходится прибегать к дальнейшим упрощающим предположениям, связанным с разбиением окружающего антенну пространства на дальнюю, промежуточную и ближнюю зоны.

Введем сферическую систему координат R , 0 , Ф , центр О которой помещен внутри излучающей системы (рисунок 2). Точки Q ( x ', y ', z ') и P ( x , y , z ) будут изображать соответственно текущую точку интегрирования внутри излучающей системы и точку наблюдения в окружающей однородной среде. Расстояние r , входящее в показатель экспоненты и в знаменатель подынтегрального выражения (6) равно:

r = QP = 4R ² + R '² - 2 RR ' cos a ,       (7)

где α – угол между направлениями OQ и OP .

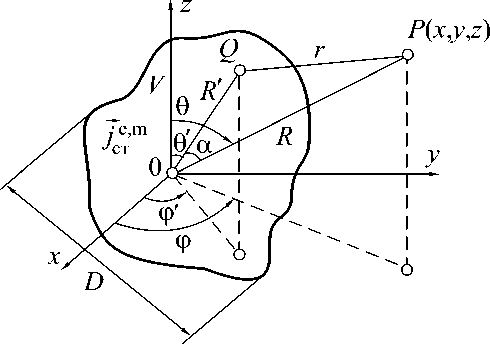
Рисунок 2. К расчету ЭМП излучающих систем

Если R >  R' , т.е. точка наблюдения P находится на достаточном удалении от объема V , занятого токами излучающей системы, то расстояние r можно представить в виде ряда по возрастающим степеням отношения R'/R (8).

D П R'         R'2 а 2 \ r = R 1--cos a +--- 1 - cos a +

R       2 R⁷

+---cosa(1 - cos2 a +...

2 R ³

Пусть R » R' , что соответствует наиболее важной для теории антенн дальней зоне. При этом в формуле (6) возможны следующие упрощения:

• 1.    Величина r в знаменателе принимается равной R , т.е. полагается, что r = R. Таким образом, множитель 1/ R можно вынести из-под знака интеграла.

• 2.    Величина r в мнимом показателе экспоненты подынтегральной функции полагается равной:

r « R - R ' cos a . (9)

Это означает, что лучи, проведенные в точку наблюдения дальней зоны из начала координат и из текущей точки интегрирования в объеме V , считаются параллельными (рисунок 3). Добавок R' cos _a к величине R носит название разности хода лучей, учитывающей запаздывание сферических волн, приходящих в бесконечно удаленную точку наблюдения P от двух элементарных источников, располагающихся в начале координат и в текущей точке интегрирования Q ( x ', y ', z ') .

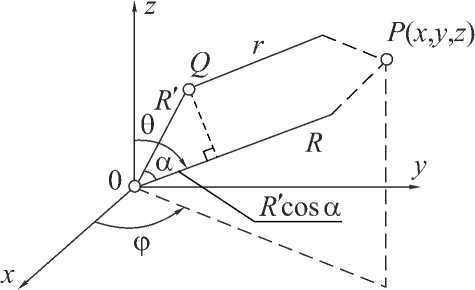
Рисунок 3. К расчету разности хода лучей

1    8 A r

R sin 0 8ф

—

R8R(RA ф)

^— 1 8

+1 ф R 8R(RA0)

+

——

8 a r —

Подставляя (13) в с учетом (14) и пренебрегая членами, имеющими радиальную зависимость 1 R ² и 1 R ³ в соответствии с определением дальней зоны, после ряда тождественных преобразований получаем:

В расчетном соотношении разность хода

R' cos а представляет собой проекцию вектора:

^   —

R' = ixR ' sin 0' cos ф' + iyR ' sin 0' sin ф' +

—*

——          ——           ——

^{—           —     —      —}

+ izR cos 0 = ixx + iyy + izz

— Е 0 =	- i 2 п X	— e    — Z a A 0» + A ф»	— ; H ф	= E 0 . Zc
— Е ф =	- i 2 п X	— e    — m Z a A ф» A 0»	— ; H 0	= - E — ф = Zc ’	(15)

Er = 0; Hr = 0,

на направление единичного вектора, исходящего из начала координат в точку наблюдения:

R —   —               —               —

— = i _x sin 0 cos ф+ iy sin 0 sin ф + i _z cos 0 . (11)

Скалярно умножая векторы (10) и (11), находим явные выражения для разности хода:

R' cos a = x’ sin 0 cos ф + y’ sin 0 sin ф + z' cos 0 = = R '[ sin 0 sin 0' cos ( ф - ф' ) + cos 0 cos 0'].

Использование сформулированных выше упрощений пп. 1 и 2 в формуле (6) приводит к асимптотической формуле для векторного потенциала в дальней зоне:

A»’ m (R, 0, ф)=                 (13)

= —P^-—- j j ^{e ,} m ( x ', y ', z ') exp ( ikR' cos a ) dV .

^П V

Для перехода от векторных потенциалов A m m ( R , 0 , ф ) к векторам полей E — и H в дальней зоне необходимо выполнить операции, предписываемые соотношениями (4). Основные формулы векторного анализа в сферической системе координат имеют следующий вид (14):

f = div A = X—( r ² a_r ) +

R ² 8 R^[     R’

1     8                1    ⁸ A ф

+--(sin0A0) +--,

R sin 0 80^v          R sin 0 8ф

, j— grad div A = grad f = iRh

^R 8 R

j  j rot A = iR

f ₊ ^j      f ,

R 80 ф R sin 0 8ф

R sin 0

—(sin0A } 80[

—

8 A 0

8ф

+

где Z^ = ц ^ ^ /е ^ - волновое сопротивление среды; 1 - длина волны в среде, т.е. X = Xо/ уЩл ; X 0 - длина волны в вакууме;

е и ц - относительные диэлектрическая и магнитная проницаемости.

Заключение

По результатам исследования можно сделать следующие выводы.

• 1.    Поле излучения, сформированное системой связи с обеспечением формирования импульсного сигнала с изменяющейся по заданному закону частотой вращения вектора поляризации, представляет собой суперпозицию двух волн с левой и правой круговыми поляризациями соответственно, а не волну с вектором поляризации, вращающимся с частотой, независящей от частоты несущей.

• 2.    В результате эксперимента установлено, что коэффициент прохождения волн с круговой поляризацией через неоднородную среду практически не отличается от коэффициента прохождения линейно поляризованных волн в условиях аналогичной среды. При этом, результаты проведенных испытаний подтвердили высокий уровень затухания радиоволн при прохождении через среды. Также установлено, что существенной зависимости затухания от вида поляризации не установлено. Возможность организации радиосвязи повышенной эффективности в УВЧ – СВЧ диапазонах в условиях неоднородной среды за счет управления видом поляризации не подтвердилась.

• 3.    ЭМВ с продольными составляющими вектора E и H в свободном пространстве существуют, однако эти продольные составляющие убывают пропорционально 1 R ³ , в то вре-

мя как их поперечные составляющие убывают пропорционально 1/ R . Никакими уникальными свойствами такие волны не обладают. Создание систем связи с обеспечением формирования продольных электромагнитных волн нецелесообразно вследствие их быстрого затухания.