Исследование возможности использования гранично-ранговых кодов в криптографии ГПТ

В настоящее время безопасность сети является одним из важнейших аспектов в процессе обмена, информацией. Были предприняты различные меры для борьбы с угрозами безопасности информации. Криптография является одним из методов, который позволяет осуществлять безопасную передачу данных без потери конфиденциальности и целостности. На основе распределения ключей, криптосистема, подразделяется на. два. основных типа: криптосистема, с симметричным ключом и криптосистема, с асимметричным ключом.

Существует множество классификаций алгоритмов шифрования, но чаще всего используется классификация ключей. Симметричная криптосистема, или криптосистема с секретным ключом, использует один и тот же ключ как для шифрования, так и для расшифрования. Асимметричная криптосистема, или криптосистема, с открытым ключом, разработана, таким образом, что ключ, используемый в процессе шифрования, отличается от ключа, используемого в процессе расшифровки.

Асимметричные криптосистемы также известны как криптосистемы с открытым ключом (РКС); характеризуются тем, что ключ, используемый в процессе шифрования, отличается от ключа, используемого в процессе расшифровки. Эта система намного более безопасна, чем симметричная криптосистема, когда, шифровщик не может расшифровать шифрованные данные с помощью чужого открытого ключа. Фактически это является главным преимуществом криптосистемы. Рисунок 1 описывает криптосистему с открытым ключом [1].

«Московский физико-технический институт (национальный исследовательский университет)», 2019

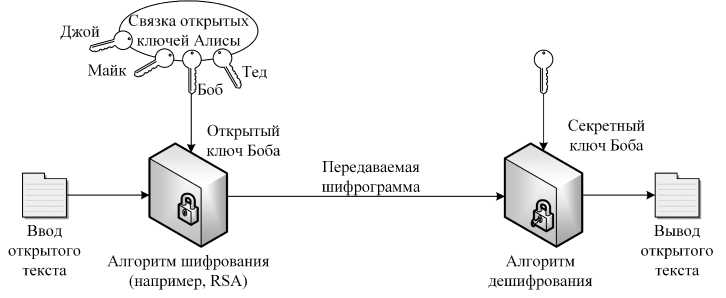
Рис. 1. Криптосистема с открытым ключом

Статья организована следующим образом. В разделе 2 обсуждены задачи кодирования для метрических пространств с гранично-ранговой и ранговой метриками. В разделе 3 приведены криптосистемы ГИТ и их варианты. Здесь обсуждены также различные виды атак в системе ГИТ.

2.    Метрики и коды

Для заданного множества X мы говорим, что X является метрическим пространством, если оно оснащено специальной функцией d ( x,y ) которая может вычислять расстояние между любыми двумя точками x,y из X. В частности, d должен удовлетворять аксиомам метрики. Сейчас наша цель - рассмотреть и сравнить коды в гранично-ранговой и ранговой метрике.

2.1.    Гранично-ранговая метрика

• Э.М. Габидулиным [2], [3] были введены граничные коды, исправляющие ошибки решетчатой конфигурации. Коды могут исправить ошибочные строки и столбцы.

0 ... 0

Let GF ( q ) - базовое конечное поле, a GF ( q^т ) - его расширение степени т. Пространство векторов GF ( q^т ) ^т длины т снабдим ранговой весовой функцией: ранговый вес вектора 9 = ( 91 92 ... 9_т ) С GF ( q^т ) ^т равен максимальному числу координат, линейно независимых над базовым полем.

Линейное пространство матриц над полем GF ( q ) с размерами т х п обозначается GF ( q ) ^тхп. Оно состоит из матриц

«1,1		«1,2     .	• .    «1,п
	«2,1 • • •	«2,2    . •                   • • •	. .    «2 ,п • •                       • •                 •	, « i,j С GF ( q )
м =
	\ «т, 1	« т, 2   .	. .  « т,п/

Определение 1. Гранично-ранговая метрика над GF(q ). Граничный ранг x над q определяется как p(x\q ) = p(A\q ). Граничный ранг для A, обозначаемый p(A) равен минимальному числу линий (строк и столбцов), в которых содержатся все ненулевые элементы матрицы A над GF(q ).

Функция p(A) удовлетворяет всем аксиомам нормы [4]:

( 0 ... 0 \

• 3) | p( A i) - p( A 2) | <  p( A i + A 2) <  p( A i) + p( A 2).

Максимальный граничный ранг, очевидно, равен

D = max | A| = тіп(т, п )

Определение 2. Гранично-ранговое расстояние. Пусть A i и A 2 - два кодовых слова длины п с элементами из GF ( q ^m) Расстоянием между матрицами A i и A 2 называется граничный ранг их разности:

d( A i, A 2) = p( A i — A 2).

Код С, имеющий длину п, к информационных символов и минимальное граничноранговое расстояние d, называется линейным гранично-ранговым кодом С\т х п, k,d\

Параметры С \ т х n,k,d \ гранично-ранговых кодов

• 1)    Длина кодового вектора - п. Размер соответствующей кодовой матрицы - т х п.

• 2)    Число кодовых векторов или кодовых матриц - q^k.

• 3)    Минимальное кодовое расстояние - d.

• 4)    Код позволяет исправлять ошибки, граничный ранг которых равен или меньше t = \(d — 1)/2\.

Произвольный набор (т х п)-матриц кода С = {Ci, C2,..., См } называется кодом с .мощностью М.

Обозначим код С \ п х n,M,d \ с числом кодовых матриц М и гранично-ранговым кодовым расстоянием dTR = d. Задача кодирования состоит в выборе кода с максимальным значением М при заданном расстоянии dTR = d.

Следующая лемма описывает верхнюю границу типа синглтона для мощности кода М.

Лемма 1. Пусти существует код С\п х п, М, d\. Тогда logq М      d — 1 _ d — 1

< 11

• п ²         Р тах         п

Пусть F_n - сопровождающая матрица, примитивного многочлена, степени п (ем. (2)). Запишем порождающую матрицу кода МГРР С_s+i\n х п, (п — s)п, s + 1\ в систематическом виде C_s+i:

⎛ x0 ⎞ xn—s—i

• ^x0^Fn ^{+ х}1^ҒП⁺ • • • ⁺ xn—s—iF^{n S}

  Fn

  
  

  0   1   0

  0   0   1

  
  
  
  

  /0  fi

2.2.    Ранговая метрика

.. / n — i)

Ранговое расстояние было введено Э.М. Габидулиным в 1985 году [5].

Let GF ( q^ - базовое конечное поле, a GF ( q^m^ - его расширение степени т. Пространство векторов GF ( q^m ) ^m длины т снабдим ранговой весовой функцией: ранговый вес вектора 9 = ( 91 92 ... 9_m) € GF ( q m ^m равен максимальному числу координат, линейно независимых над базовым полем.

Ранг матрицы Rk ( M ) определяется как максимальное число линейно независимых над GF ( q ) строк (или столбцов).

Ранговая норма матрицы (или ранговый вес матрицы) определяется как ее ранг:

N ( M ) = Rk ( M ).

Линейный векторный ранговый [т, k,d]-кoд над GF(q^m^ — это к-мерное подпространство пространства векторов GF ( q^m ) ^m с ранговым расстоянием d. Число векторов в к-мерном подпространстве равно q^mk.

Из границы синглтона следует к < т — d + 1.

Если достигается знак равенства, то код называется кодом с максимальным ранговым расстоянием (МРР-кодом).

Линейный код задается порождающей матрицей G размера к х п и ранга к либо проверочной матрицей Н размера ( п — к ) х п и ранга п — к такой, что

GH^Т = 0.

Конструкции векторных ранговых [п, к, d] МРР-кодов:

Hd-1 = Һ1 Һ1 F һ2       . . . һ2      .. h2   .. һп һп һП , ... «1- ...    ... ht-  .. ... qd-2 һп Gk = 91 91 q2 91 92       ... 92    ... 12 9і        ... 9п 9п 12 9П ,                                          (3) ... qk-1 91 ...    ... qk-1 9-2             ... ... qk-1 9П   J где элементы 91,92,... ,дп из GF(qm) линейно независимы над GF(q).

2.3.    Вывод

Видно, что ранговый код и гранично-ранговый код имеют много общего, поскольку оба являются линейными кодами.

Результаты исследования показывают существенные различия между граничноранговой метрикой и ранговой метрикой и дают понимание, что гранично-ранговая метрика больше подходит для исправления ошибок решетчатой конфигурации.

3.    Система ГПТ

Первоначальная система ГПТ с открытым ключом предложена Э.М. Габидулиным, А. В. Парамоновым, О. В. Третьяковым в 1991 году [6].

Первоначальная система ГПТ

Эта система предложена в [6], а ее вариант - в [7].

Открытый текст - это любой к-вектор m = (m_i, m2, ..., m k ) ,m_i Е GF ( q^pi = 1, 2,... , к.

Открытый ключ - это к х п матрица

GCT = S(G + X), где матрица. G имеет вид (3).

S - невырожденная к х к перемешивают пая матрица.. X - случайная к х п мат рица, называемая укрывающей или искажающей матрицей. Она. должна, иметь ранг r( X | GF(q)) = ti < t, где ti - параметр проектирования.

Секретный ключ - это матрицы S , G , Хи (неявно) быстрый алгоритм декодирования МРР кода.

Шифрование: пусть m - открытый текст. Тогда шифротекст задается соотношением c = mGcr + e = mSG + (mSX + e), где e - искусственна я ошибка ранга t2 = t — ti или меньше. Эта ошибка должна выбираться случайно.

Расшифрование: легальный пользователь, получивший шифротекст, применяет к c быстрый алгоритм декодирования и получает вектор mS. Затем он умножает этот вектор справа на матрицу S ^{- 1} и восстанавливавт открытый текст m. Для любого открытого текста m верно псу>авепство r ( mSX + e | GF ( q )) <  r ( mSX | GF ( q )) + r ( e | GF ( q )) <  t1 + ( t — t1 ) = t. поэтому пользователь всегда, восстанавливает открытый текст правильно.

В этой системе размер открытого ключа в битах равен кпN log2 q, а информационная скорость - к/п.

Модификация системы ГПТ

Открытый ключ - это матрица

G open = S ([ O G ] + [ X i X 2 ]) P .

Здесь

S - невырожденная квадратная матрица порядка к с элементами из расширенного поля GF(qⁿ) выбранная случайно. Это строчный скремблер;

О к х т матрица, состоящая из нулевых элементов;

G - порождающая матрица МРР кода вида (3) с порождающим вектором g:

Xi - некоторая к х т матрица, свойства которой мы обсудим ниже. Это первая искажающая матрица;

X 2 - к х п матрица такая, что r( X 2|GF(q)) = ti. Это вторая искажающая матрица;

P - невырожденная матрица порядка п + т с элементами из базового поля GF ( q). Это столбцевой скремблер.

Невырожденная матрица P не только перемешивает столбцы матрицы G, но и перемешивает их со столбцами искажающей матрицы Xi. Это усиливает криптостойкость системы по отношению к структурным атакам.

Шифрование: пусть m - информационный к-вектор (открытый текст). Тогда шифротекст вычисляется как c = mG open + e, где e - вектор ікжуеетвеішвіх ошибок ранга t2 = t — ti = [(п — к)/2] — ti.

Расшифрование: после получения шифротекста c легальный пользователь вычисляет с‘ = (с!,с2,..., <+т) = cP-i = mS([O G] + [Xi X2]) + eP-i.

Из вектора с‘ он извлекает подвектор c" = (ск+1,ск+2,..., с'п+к) = mSG + mX2 + e", где e" - подвектор eP-1. Следовательно, r(e‘‘IGF(q) < t2. Отсюда следует (принимая во внимание. что r(mX2|GF(q)) < t1) r(mX2 + e‘‘|GF(q)) < t1 +t2 = t.

Применяя к вектору c ’’ быстрый алгоритм декодирования, легальный пользователь на ходит вектор mS и открытый текст как вектор m

3.1.    Атаки в системе ГПТ

В работах [8] Гибсон разработал две структурные атаки для криптосистемы ГПТ и доказал, что наборы параметров, предложенные в [6] и [7], небезопасны. Недостатком атак Гибсона является то, что они имеют экспоненциальное время выполнения, если секретный ключ тщательно выбран. Для противостояния атакам Гибсона было предпринято несколько попыток изменить криптосистему ГПТ, но большинство из этих вариантов опираются на предположения о безопасности, очень похожие на те, что были в первоначальном предложении (см. [9]).

В работе [10] Р. Овербек построил новую структурную атаку на криптосистему ГПТ. В отличие от атак Гибсона, она имеет полиномиальное время выполнения, полностью разрушает первоначальную криптосистему ГПТ из [6] и применима к предложенным до сих пор вариантам ГПТ vl, v2, v3.

В работе [11] был представлен другой вариант ГПТ, основанный на надлежащем выборе матрицы скремблера столбцов над полем расширения. Этот вариант защищен от всех известных атак.

4.    Заключение

Рассмотрена криптосистема ГПТ с первоначальной системой и столбцевым скремблером. Показана эквивалентность различных представлений криптосистемы по отношению к криптоанализу, а также показана общая форма открытого ключа для криптоанализа. Показано, что существует возможность применения гранично-ранговых кодов в криптосистеме.