Исследование возможности применения генетических алгоритмов для реализации криптоанализа блочных криптосистем

Введение. В настоящее время при разработке компьютерных технологий, обеспечивающих информационную безопасность и защиту информации, широкое применение находят криптографические методы защиты. Для решения задач криптоанализа, относящихся к классу NP -полных, в последние годы применяются алгоритмы, основанные на природных системах. К ним относятся методы моделирования отжига, генетические алгоритмы (ГА), эволюционные методы, алгоритмы роевого интеллекта и т.д. В моделях и алгоритмах эволюционных вычислений ключевым элементом является построение начальной модели и правил, по которым она может изменяться (эволюционировать). В течение последних лет были предложены разнообразные схемы эволюционных вычислений, в т.ч. генетический алгоритм, генетическое программирование, эволюционные стратегии, эволюционное программирование.

В работе [1] рассматривались задачи криптоанализа и приведены результаты криптоанализа классических симметричных криптографических алгоритмов с использованием методов эволюционной оптимизации и генетического поиска для симметричных шифров перестановок, а также для реализации шифров простой и многоалфавитной замены. Среди обзорных работ, посвященных описанию методов и перспектив развития криптоанализа, следует отметить [2–4], в которых описаны универсальные методы (метод полного перебора, атака по ключам, частотный анализ, метод Полларда), методы криптоанализа симметричных (статистический метод, метод дифференциального анализа, метод линейного анализа) и асимметричных (задача дискретного логарифмирования, задача факторизации) криптосистем, а также новый вид криптоанализа — атаки по побочным каналам. В работе [2] также приводится краткое изложение новых технологий, связанных с использованием ГА, нейронных сетей и квантовых компьютеров.

Криптоанализ асимметричных алгоритмов шифрования описан в [4–6], где представлен ГА для решения задачи определения вариантов разложения заданного числа N на множители и ГА разложения заданного числа на два взаимно простых сомножителя, а также алгоритм нахождения простого делителя числа. В работе [7] представлены алгоритмы муравьиных и пчелиных колоний для разложения составных чисел на множители путем определения делителя числа с заданной точностью в заданном интервале. Описание алгоритма «пчелиных колоний» для реализации криптоанализа шифров перестановки, и сведение его к классической задаче о назначениях приведено в [8]. Метод криптоанализа блочного алгоритма. Таким образом, возникает вопрос о возможности применения биоинспирированных методов для криптоанализа современных блочных алгоритмов шифрования, т.к. переход к блочному шифрованию открывает дополнительные возможности для повышения стойкости криптоалгоритмов. Одним из приемов при шифровании является многократная, состоящая из нескольких циклов, обработка одного блока открытого текста. Основные принципы построения блочных шифров, структура алгоритмов блочного шифрования (схема Фейстеля) описаны, например, в [3].

Отличительной особенностью применения биоинспирированных методов криптоанализа (в частности, ГА) является возможность использования самого алгоритма шифрования (или расшифрования) в качестве целевой функции для оценки пригодности ключа, определенного с помощью генетических операций. Поэтому можно утверждать, что при использовании ГА процесс определения секретного ключа (например, при криптоанализе второго типа) зависит не столько от сложности шифрующих преобразований, сколько от самого биоинспирированного метода, который должен обеспечивать достаточное разнообразие генерации ключей. В этой связи задача исследования возможности применения биоинспирированных алгоритмов для криптоанализа блочных криптосистем является, несомненно, актуальной.

Рассмотрим организацию криптоанализа блочных методов с использованием ГА на примере представителя блочных шифров — стандарта DES.

Заметим, что важным свойством как блочных методов, так и ГА, является их внутренний параллелизм, основные модели параллельных ГА (глобальный параллельный ГА, островная модель, клеточный ГА) приведены в [1]. В этой связи для разработки криптоанализа данного алгоритма с помощью эволюционного подхода рассмотрим вначале процесс параллельной реализации составляющих его этапов. Исходя из непосредственного описания алгоритма, можно выделить следующие основные параллельно выполняемые этапы:

• -    параллельная обработка 64-битовых блоков шифртекста;

• -    параллельная обработка восьми 6-битовых блоков B … B ;

• -    параллельная обработка блоков C и D и формирование ключей K .

С использованием этих очевидных преобразований схема одного цикла алгоритма представлена на рис. 1 [9].

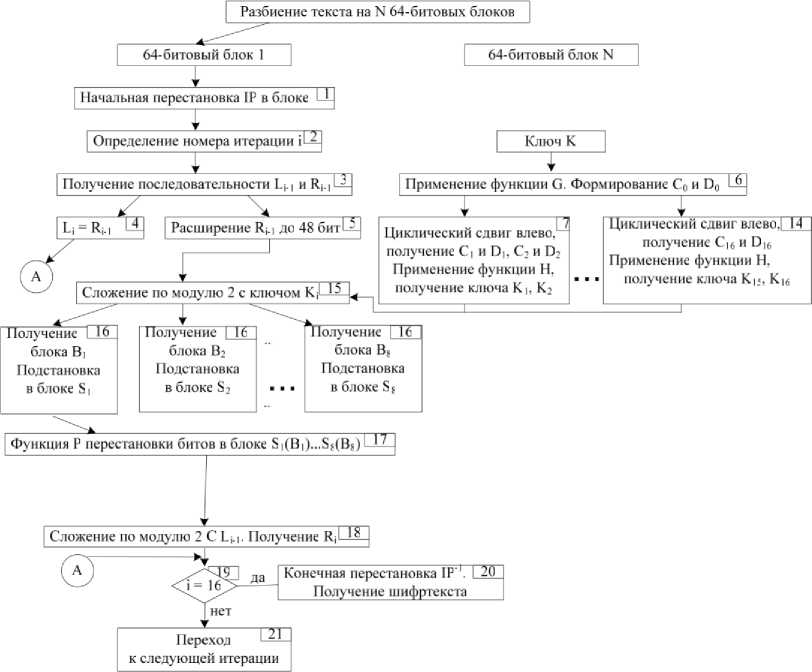
Рис. 1. Структурная схема цикла алгоритма DES

Для дальнейшего определения множества независимых операторов, допускающих параллельное выполнение, используются методы, описанные в [10, 11].

Построим информационно-логическую граф-схему G = ( Х , U) алгоритма DES, где множество Х вершин соответствует множеству операторов алгоритма, множество U дуг состоит из дуг, определяющих связи по управлению (двойная линия) и по информации (одинарная линия). Граф-схема алгоритма позволяет представить и проанализировать как общую структуру алгоритма, так и связи между отдельными операторами, и показана на рис. 2.

Для данного графа введем в рассмотрение матрицу следования S . Элемент S ( ij ) = * , если существует связь по управлению ( j' ^ i ) и S ( ij ) = 1, если существует связь по информации ( j' ^ i ).

Используя алгоритм нахождения транзитивных связей, получим матрицу S T [10, 11]. Далее введем в рассмотрение матрицу L логической несовместимости операторов, используя алгоритм, также приведенный в [10, 11]. Для объединения информации о логической несовместимости операторов и их информационно-логической связи откажемся от ориентированности графа G и построим матрицу S T ', полагая ( i , j ) = ( j' , i ) = 1.

На матрицу S T ' наложим матрицу L , определив значение каждого элемента по правилам дизъюнкции. Получим матрицу независимости M , по нулевым элементам которой в строке (пробелам) можно указать множество тех операторов, каждый из которых может быть выполнен параллельно с оператором, соответствующим номеру строки. Структуры матриц S , S T , L , S T ', М приведены в [9].

Таким образом, на основе построенной параллельной схемы алгоритма представим метод криптоаналитической атаки второго типа, т.е. при наличии известного текста и шифртекста требуется определить ключ K , используемый для шифрования, с целью дешифрования других сообщений, зашифрованных тем же ключом.

Поскольку секретность DES полностью определяется ключом, задачей эволюционного поиска является генерация популяции ключей и оценка их оптимальности с последующим применением стандартного набора генетических операций. То есть применение генетического поиска непосредственным образом для проведения криптоаналитической атаки второго типа при заданных 64-битовых блоках исходного текста и шифртекста можно представить структурной схемой, ГА показанной на рис. 3 (на схеме K j : i — номер индивидуума в популяции, j — номер варианта, используемого на j -й итерации).

Информатика, вычислительная техника и управление

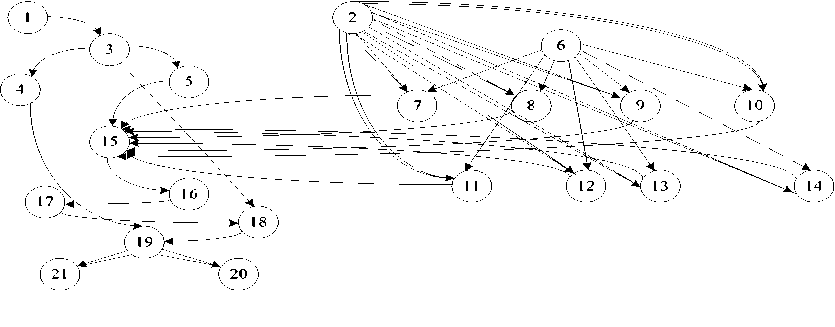
Рис. 2. Информационно-логическая граф-схема алгоритма DES

Как видно из схемы (рис. 3), после формирования начальной популяции ключей производится оценка их пригодности (определение целевой функции), т.е. проверка, насколько полученный с их помощью шифртекст совпадает с известным. После оценки производится селекция индивидуумов популяции для проведения множества генетических операций и получения множества потомков, далее полученная расширенная популяция подвергается дальнейшему оцениванию. Процесс заканчивается, когда прекращается эволюционирование популяции, либо когда исчерпан заданный временной ресурс (пройдено заданное количество генераций).

Следовательно, если сформирована популяция из P индивидуумов, то время работы алгоритма T составит T = Pt , где t — время оценки одного индивидуума (варианта ключа).

При значительном объеме популяции для определения функции пригодности индивидуумов можно использовать эффективный принцип организации специализированных вычислений — принцип конвейера [12]. Общая схема реализации потока операций на последовательном конвейере и описание процесса реализации представлены в [9].

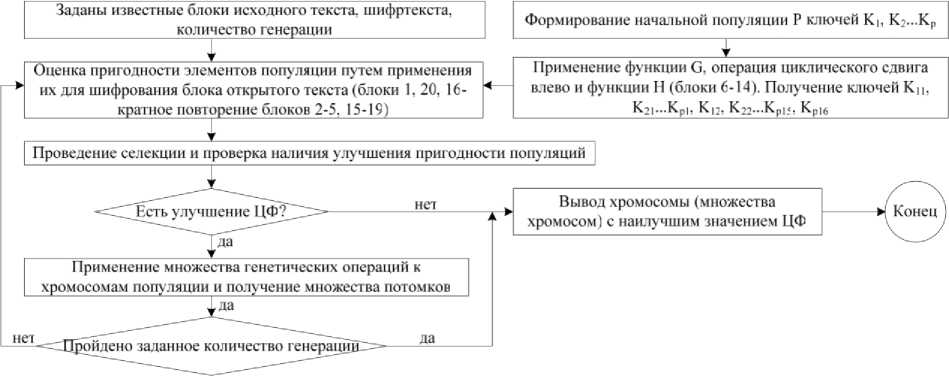
Рис. 3. Структурная схема генетического алгоритма

Таким образом, после разработки параллельной схемы реализации криптоанализа актуальной является задача: для алгоритма шифрования, используемого для оценки пригодности элементов популяции ключей, на основе построенного информационно-логического графа G и для заданного времени Т зад найти необходимое наименьшее число процессоров однородной вычислительной системы и план выполнения операторов на них. Для решения этой задачи также использовались методы, изложенные в [10, 11], а ее решение представлено в [13]. При этом на основе визуальной методики [11] получена минимальная оценка числа процессоров n =2 при критическом пути в графе G Т _кр=24, заданном времени Т _зад= Т _кр и показано, что эта оценка является минимальной, а также определен план выполнения операторов.

На основе построенной параллельной схемы алгоритма разработан метод криптоаналитической атаки второго типа. Алгоритм и его программная реализация включают следующие этапы:

• 1.    Генерация популяции ключей по 64 бита (размер определяется экспериментально).

• 2.    Оценка каждого элемента (ключа) популяции (блок CheckQuality).

• 3.    Сортировка ключей по степени пригодности (блок QualitySolutionSort).

• 4.    Проведение генетических операций (кроссинговер 80%, мутация и инверсия 0,05%).

• 5.    Оценка расширенной популяции.

• 6.    Сокращение популяции на 20% путем отсечения самых худших индивидуумов.

• 7.    Возврат к 3.

Процесс заканчивается либо по истечении временного ресурса, либо по достижении оптимального или квазиоптимального варианта ключа.

Экспериментальные результаты. Приведем описание некоторых экспериментальных результатов, полученных при реализации ГА криптоанализа, проводимого с использованием процессора CORE I5-2400. Результаты для двух серий экспериментов представлены в таблицах 1, 2. При реализации эксперимента задавались следующие параметры: размер начальной популяции — 1000; количество итераций — 100; норма мутации и инверсии — 0,05; тип кроссинговера — простой двухточечный.

Таблица 1

Результаты сходимости ГА криптоанализа при 1 генерации

0	1000	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5
1	1800	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5
4	5372	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5
5	7735	25,0	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5
8	23094	25,0	25,0	25,0	25,0	25,0	25,0	25,0	25,0	25,0	25,0
17	614816	37,5	37,5	25,0	25,0	25,0	25,0	25,0	25,0	25,0	25,0
18	885334	37,5	37,5	37,5	37,5	37,5	37,5	37,5	25,0	25,0	25,0
20	1835828	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5
22	3806771	50,0	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5
23	5481748	50,0	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5
25	11366950	50,0	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5
30	23681145	62,5	50,0	50,0	50,0	50,0	50,0	37,5	37,5	37,5	37,5

В 1 столбце таблиц показан номер итерации, во 2 столбце — количество хромосом, подвергнувшихся мутации и инверсии, столбцы с 3 по 12 значение процента для 10 лучших хромосом популяции, определяющего совпадение полученного текста с исходным. Как видно из таблицы, на 25 генерации наилучшая хромосома обеспечивает совпадение полученного текста с исходным на 50%, на 30 генерации — на 62,5%.

Таблица 2

Результаты сходимости ГА криптоанализа при 2 генерации

0	1000	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5
1	1800	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5
4	5372	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5
5	7735	25,0	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5	12,5
8	23094	25,0	25,0	25,0	25,0	25,0	25,0	25,0	25,0	25,0	25,0
15	294570	37,5	37,5	37,5	25,0	25,0	25,0	25,0	25,0	25,0	25,0
16	423775	50,0	37,5	37,5	37,5	37,5	25,0	25,0	25,0	25,0	25,0
17	614816	50,0	37,5	37,5	37,5	37,5	37,5	25,0	25,0	25,0	25,0
18	877847	50,0	37,5	37,5	37,5	37,5	37,5	25,0	25,0	25,0	25,0
20	1818165	50,0	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5
21	2618158	50,0	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5	37,5
25	11360920	50,0	50,0	50,0	37,5	37,5	37,5	37,5	37,5	37,5	37,5
30	23681145	62,5	62.5	50,0	50,0	50,0	50,0	37,5	37,5	37,5	37,5

Время реализации алгоритма для получения квазиоптимального ключа составило при одноточечном кроссинговере (мутации и инверсии 5%) 53 мин., при кроссинговере по маске 29 мин., при двухточечном кроссинговере 55 мин., что значительно меньше временных затрат при реализации дифференциального криптоанализа, приведенного в [14].

Информатика, вычислительная техника и управление

Приведем результаты эксперимента по определению квазиоптимального ключа, обеспечивающего максимальное совпадение полученного текста с исходным. В качестве исходного был использован следующий текст: «я_вас_любил:_любовь_еще,_быть_может,_в_душе_моей_угасла_не_совсем;_но_пусть_она_вас_больше_не_тревожи

т;_я_не_хочу_печалить_вас_ничем.___»

При реализации алгоритма криптоанализа путем разбиения исходного текста на 8-буквенные блоки и использовании параллельного вычислительного процесса был определен квазиоптимальный ключ, обеспечивающий получение следующего текста:

«я*в*с*любил***юб*вь*еще**б*ть_*оже***в_д*ше*м*ей_**асла*не**овс*м*_н*_*ус*ь*о*а_в*с*бол**е_н*_т*ев*

ж*т;*я*н**хочу_п*ч*л*т*_ва*

**че*.  *»

Как можно заметить, полученный текст достаточно близок к исходному (совпадение в пределах 62,5%), содержит осмысленные слова (хочу, любил) или почти осмысленные (т*ев*ж*т, п*ч*л*т), из чего следует, что процесс расшифрования (например, при использовании ГА для криптоанализа первого типа) может быть доведен до конца вручную (аналогично тексту, полученного при использовании квазиоптимального ключа в ГА, описанном в [15]).

При втором эксперименте в качестве исходного был использован следующий текст:

«жил_старик_со_своею_старухой_у_самого_синего_моря;_они_жили_в_ветхой_землянке_ровно_тридцать_лет_и_три _года._старик_ловил_неводом_рыбу,_старуха_пряла_свою_пряжу._раз_он_в_море_закинул_невод,_-_пришел_невод_с_одною_тиной.____»

При реализации алгоритма криптоанализа и использовании параллельного вычислительного процесса был определен квазиоптимальный ключ, обеспечивающий получение следующего текста:

«жи*_с*а*и*_с*_сво*ю_*т*ру*ой_у_с**ог*_си*е*о_мо*я**о*и_**ли_в_в*тхо**з*мля*к*_р*вн**три**ат**лет*и_тр и***да.*с*а*и*_лов*л*н*в*до*_рыб*,**та*уха**ряла*с**ю_*ряж*._р*з*о*_в*мор**зак***л_н*вод*_*_***шел_**во д_с**дною*т*ной*__**»

Таким образом, при размере начальной популяции N=1000 был определен квазиоптимальный ключ, что свидетельствует о возможности экспериментального выбора параметров ГА. При экспериментальной реализации использовались простой одноточечный кроссинговер, кроссинговер по маске, двухточечный кроссинговер с нормой 80%, простая точковая мутация с нормой 5%. В процессе реализации ГА после формирования множества потомков и проведения генетических операций использовался элитный отбор для доведения размера популяции до исходного состояния. В случае, если при реализации алгоритма криптоанализа был определен квазиоптимальный ключ, обеспечивающий совпадение полученного текста с исходным на 62,5% и более, результат криптоанализа считался достигнутым.

Заключение. Описано применение ГА для реализации криптоанализа блочных криптосистем, приведены результаты эксперимента при реализации криптоанализа второго типа алгоритма DES на основе параллельной схемы его реализации. Временные затраты алгоритма не превосходят временных затрат при реализации известных методов криптоанализа. Как показали результаты эксперимента, полученные результаты по определению оптимального ключа (при криптоанализе второго типа) в общем случае в значительной степени зависят от длины исходного текста, что может привести к эффективному использованию вычислительных систем, допускающих параллельную обработку информации (в частности, многопроцессорных систем класса SIMD).