Исследование возможности снижения коррупции в России на основе математических многофакторных моделей

Antipin I. В., Volodina Y. I. Research of the possibility of reducing corruption in Russia based on mathematical multi–factor models. System Analysis in Science and Education, 2020;(4):1–9(In Russ). Available from: DOI: 10.37005/2071-9612-2020-4-1-9.

В настоящее время существует проблема глобального и системного характера – коррупция. Сущность данной проблемы выражается в том, что сегодня коррупция угрожает всей национальной безопасности РФ. Также она не дает нормально развивать гражданское общество и институты демократии нашего государства, строит значительные препятствия для осуществления гражданами России своих конституционных прав в области социальной сферы, образования и науки, медицины и здравоохранения, имущественных отношений и пр.

Коррупциогенность в РФ создает угрозу стабильности в обществе, ухудшает экономическую стабильность экономики, негативно сказывается на благосостоянии населения, портит имидж страны на международной арене. Для эффективной борьбы требуется подготовка компетентных кадров на административные должности, улучшение эффективности работы государственных и муниципальных аппаратов [1].

• 1.    Актуальность темы

В современном российском обществе коррупция приобрела очень важное место. Даже при том, что наблюдаются некий спад ее проявления в последние 10 лет, но большая часть отечественной экономики все еще не может выйти из серой зоны. Поэтому наблюдается торможение большинства значимых процессов, которые относятся к гос. расходам (гос. закупки или строительство гос. объектов).

Стоит отметить, что, по данным общественных опросов, гражданам нашего государства, зачастую, проще привыкнуть или закрыть глаза на коррупцию. Поэтому народ уже не приравнивает ее ко злу, а даже наоборот, в некоторых ситуациях принимает ее как должное в современном интеграционном обществе. Большая часть современной молодежи на первое место ставит карьеру, то есть стремление скорейшего занятия высшей должности, для последующего обеспечения комфортной и беззаботной жизни. Аморальные и нелегальные средства достижения поставленной цели сегодня допускаются обществом, и даже в некоторой степени оправдываются [2].

Кроме этого, коррупционные преступления становиться причиной снижения экономического роста РФ. Финансовые потери от коррупции к началу 2008 года составляли порядка 1 трлн. рублей [3]. Ухудшение международного имиджа страны может привести к экономической и социальной изоляции РФ.

Так, в качестве административно-правовых методов против коррупционных действий выступают следующие [4]:

• -    система своевременного представления информации об имуществе государственного служащего, его доходах, а также имущественных обязательствах;

• -    административные запреты, которые напрямую взаимосвязаны с установленным режимом государственной гражданской службы, а также методы искоренения конфликтных ситуаций, которые возникают на почве интересов на государственной службе;

• -    при проявлении конфликта интересов – скорейшее отстранение от работы и занимаемой должности государственного служащего;

• -    замена должности государственной службы на конкурсной основе, а также определенный регламент должностей и обязанностей работника;

• -    своевременная аттестация государственных служащих, выявление примерного перечня для прохождения этапов карьерной лестницы, а также награждение и поощрение работников за соответствующие заслуги на занимаемой должности;

• -    формирование и использование кадрового резерва в рамках осуществления гражданской службы;

• -    для поступления на службу успешное преодоление вступительных испытаний, с учетом достаточного выбора кандидатов, претендующих на соответствующую должность.

• 2.    Выбор модели

• 3.    Расчет по модели

Для объективного результата прогноза степени коррупционных правонарушений в статье применяется экстраполяция математической модели, которая формируется из аналитических данных по размеру и количеству подобных правонарушений в предыдущие периоды. Такой способ прогнозирования имеет преимущество перед оценками экспертов, так как он отличается тем, что на выходе можно получить полноценный количественный прогноз.

Изучение аналитических данных позволяет не только определить уровень коррупционных правонарушений, но и рассматривается как основа для экономических и социальных механизмов, для которых моделирование требует использования математических моделей последующих типов: авторегрессий, многомерных линейных зависимостей. Предлагается также рассмотреть модели в пространстве состояний [5].

Стоит отметить, что именно линейные многофакторные модели и модели в пространстве состояния – особенно подходят для той задачи, которая подлежит решению в процессе осуществления моделирования [6].

Прогнозирование, которое производится по математической многофакторной модели содержит в себе большое количество различных аспектов, которые оказывают разного рода влияние на выбор типа модели, а также критерии такой модели, ее формирование, анализ результата, определение вероятности получения эффективного прогнозирования, и дальнейшая экстраполяция полученной в процессе исследования модели.

Из доступных временных рядов необходимо выделить неуправляемые и управляемые элементы [7]:

• -    количество цифровых (электронный) гос. услуг, шт.;

• -    средняя заработная плата административного аппарата, руб.;

• -    процент занятости населения в предпринимательстве.

Выбор факторов обусловлен тем, что рост коррупционных преступлений связан с предпринимательской активностью в стране, а также с ростом чиновнического аппарата.

Далее необходимо произвести выбор типа и способа построения модели выявления уровня коррупционной преступности, представленные в таблице 1. Критерием является динамика понижения уровня преступлений.

Таблица 1. Отбор факторов (управляемых и неуправляемых)

Год	2007	2008	2009	2010	2011	2012
Динамика снижения преступлений коррупционной направленности, %	3,41	3,49	3,54	3,57	3,58	3,95
Количество цифровых (электронных) гос. услуг, шт.	132	182	185	219	223	752
Средняя заработная плата административного аппарата, руб.	250530	276550	372162	344358	312398	384640
% занятости населения в предпринимательстве	22,7	21,8	21,9	23,5	23,4	21,1

Таблица 1. окончание

Год	2013	2014	2015	2016	2017	2018	2019
Динамика снижения преступлений коррупционной направленности, %	3,85	3,12	3,95	3,42	3,56	4,6	3,86
Количество цифровых (электронных) гос. услуг, шт.	760	1263	1235	2803	2864	2906	2813
Средняя заработная плата административного аппарата, руб.	396530	320354	286504	276860	256840	268640	289301
% занятости населения в предпринимательстве	20,2	20,3	21,3	23,2	14,3	18,3	19,3

Так, необходимо обеспечивать своевременное исключение всех факторов, на которых приходятся наименьшие показатели корреляции, рассчитанные на основании рассматриваемого критерия. Рассчитаем показатель корреляции по исследуемым переменным x и y [8]:

_    Z(x i -x)*(y i -y)

xy  ТЖ-Ху^Су-у)2, где Xi - показатель рассматриваемого фактора x; yi - показатель рассматриваемого фактора у; х -среднее арифметическое для рассматриваемого фактора x, у - среднее арифметическое для рассматриваемого фактора y.

Для расчета среднего арифметического для переменной х следует использовать формулу, приведенную ниже:

Х = -Ук-1Хк.

Получили, что по каждому из рассматриваемых факторов необходимо устранить показатель граждан, имеющих отношение к предпринимательству, поскольку корреляция по результатам расчетов была –0,31.

Следующим этапом следует в целях устранения оказания влияния со стороны размерности, нормировать критерии и факторы, для чего необходимо использовать следующую формулу:

У(0 =

y(t)  Ут1п

,

У тах ^— У тт

где Ут- = miny(t).

Все учитываемые факторы необходимо нормировать по такой же схеме. Приведем формулы, на основании которых можно рассчитать нормативные значения для критериев и факторов. При этом, в приведенных формулах не будем учитывать значение тильды, для упрощения.

Для построения показателей ЛММ динамики коррупции в Российской Федерации в течение периода с 2007 – 2019 г. следующим образом [9]:

уЮ = a0 + Xa.i *xt(t), где: a0, ai – коэффициенты модели; xi(t) – значение фактора.

Следующим шагом является произведение расчета определения всех коэффициентов, для грамотного и объективного исключения квадратичного отклонения результатов по выбранным переменным:

S = S(y(t) - ypac4(t))2 ^ min, где S – среднее квадратичное отклонение (СКО); yрасч(t) – расчетное значение критерия y.

Эту операцию можно минимизировать через программу – мастер поиск решения в Excel [10]. На основании таких расчетов получились следующие показатели: ЛММ: a0 = 0,132, a1 = 0,125, a2 = 0,257, а квадратичная погрешность аппроксимации линейной многофакторной модели в результате расчетов оказалась S = 0,266.

Дальнейшим шагом следует оценить все модели, для определения возможности их использования в нашем случае. Авторегрессии разных порядков имеют вид:

y(t) = «о + E"-i a * y(tH), где: N – порядок авторегрессии первого, второго или третьего уровня; a0, aj – коэффициенты авторегрессии.

В результате, оценили коэффициенты и значимость модели через программу MS Excel , и получили следующие результаты:

Авторегрессия первого порядка: a 0 = 0,086, a 1 = 1,03; погрешность аппроксимации (квадратичная) составляет 0,27.

Авторегрессия второго порядка: a 0 = 0,07, a 1 = 0,998, a 2 = 0,32; погрешность аппроксимации (квадратичная) составляет 0,12.

Авторегрессия третьего порядка: a 0 = 0,197, a 1 = 0,12, a 2 = 0,1897, a 3 = 1,24; погрешность аппроксимации (квадратичная) составляет 0,21.

Так, максимальная погрешность не дает возможности применения такой модели, что свидетельствует об оказании влияния на механизм большого количества разного рода факторов [11].

Далее необходимо рассмотреть МПС, представленную в виде формул, приведенных ниже:

x(t ; ) = a + В * x * (t i-1 ), y(t t ) = c + d* x(t ; ), где: B – матрица перехода; d – вектор выхода.

Результаты

a = (0,054;-0,612)T,

1,672  -0,05684

(1,0435   0,2045 .

c = 0,3654,

d = (-0,0864; -0,8564)T, где квадратичная ошибка аппроксимации составляет S = 0,066, была получена при использовании мастера поиск решения Excel.

Таким образом, особенно точно и правильно характеризует динамические показатели коррупции в Российской Федерации только МПС, что вытекает из проведенного выше анализа графиков моделей. Именно МПС имеет самый незначительный уровень отклонений, как и ЛММ, которая показала невысокое значение ошибки аппроксимации (рис. 1).

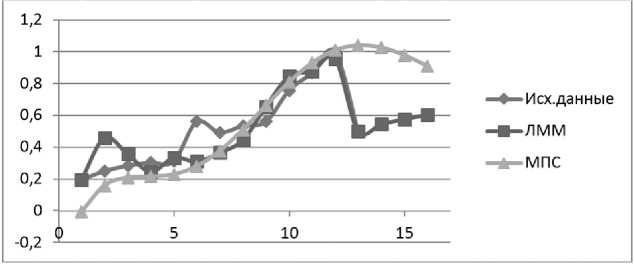
Рис. 1. Графики вариации исходов

Основной задачей исследования считаем выработку решений, имеющих непосредственную связь с разработкой соответствующих мероприятий для понижения степени проявления коррупционных преступлений в Российской Федерации, то есть особое внимание необходимо уделить именно прогнозам, получаемым посредством использования уже выбранных моделей (ЛММ, авторегрессия разныхпорядков, модель в пространстве состояний – МПС). В этой связи будем применять метод пост-прогноза: он помогает определить реакции системы по факторам. В результате данный метод можно использовать в том числе для проверки горизонта (таблицы 2-4) [12].

Таблица 2. Пост-прогноз ЛММ (2017-2019 гг.)

2007	2008	2009	2010	2011	2012	2013
0,095	0,148	0,17	0,185	0,246	0,345	0,32

Таблица 2, окончание

2014	2015	2016	2017	2018	2019
0,55	0,63	0,701	0,805	0,989	1,05

Таблица 3. Пост-прогноз МПС (2017-2019 гг.)

2007	2008	2009	2010	2011	2012	2013
0,21	0,21	0,20	0,198	0,189	0,210	0,408

Таблица 3, окончание

2014	2015	2016	2017	2018	2019
0,57	0,70	0,81	0,90	0,98	1,06

Таблица 4. Ошибки пост-прогноза (ЛММ, МПС в период 2017-2019 гг.)

Модель	Постпрогноз на 1 год	2 год	3год
Линейная многофакторная модель	8,22%	0,07%	9,65%
Модель в пространстве состояний	6,65%	0,79%	5,54%

Модель в пространстве состояний на основе расчетов в представленных таблицах имеет очень низкий уровень ошибок среди других моделей, что указывает на необходимость его использования в более углубленном будущем исследовании. Пост-прогнозный горизонт берется за 2017-2019 гг., так как такой период принято рассчитывать для точного расчета. Так необходимо осуществить прогноз развития механизма в системе влияние неуправляемого фактора (x 1 – число электронных государственных услуг).

Следующая формула характеризует ЛММ из-за изменения неуправляемого фактора [13]:

х = a+b*t, где: x – значение фактора от времени t; a, b – основные коэффициенты модели.

В результате анализа получили следующие результаты: а = –265,7, b = 0,087; погрешность аппроксимации (квадратичная) составляет 0,057.

Для подсчета авторегрессии любого порядка использовали следующую формулу:

N

x(tj) = a₀ +

^ a * x(tHy ы

Авторегрессия первого порядка: a 0 = 0,06, a 1 = 1,07; погрешность аппроксимации (квадратичная) составляет 0,09.

Авторегрессия второго порядка: a 0 = 0,08, a 1 = 0,33, a 2 = 0,84; погрешность аппроксимации (квадратичная) составляет 0,09.

Авторегрессия третьего порядка: a 0 = 0,08; a 1 = 1,19, a 2 = 0,51, a 3 = –0,74; погрешность аппроксимации (квадратичная) составляет 0,003.

Стоит отметить, что авторегрессия третьего порядка имеет самый низкий показатель погрешности аппроксимации для неуправляемого фактора x 1 .

В таблице произведено прогнозирование преступлений, связанных с коррупцией в период 20202022 гг. МПС, при спрогнозированных авторегрессий 3 порядка: управляемых ( x 2 – среднее значение зарплаты) факторах и неуправляемых ( x 1 – количество цифровых гос. услуг) (таблица 5).

Таблица 5. Прогноз факторов, 2020-2022 гг.

	2020	2021	2022
x 1	1,04	1,13	1,25
x 2	1,04	1,07	1,09
y расч	1,04	1,32	1,13

Были рассчитаны прогнозы на основе неконтролируемого фактора x 1 , при этом необходимо учитывать вариативность тренда фактора развития на ±5% отклонения от нормы (таблица 6, рис. 2).

Таблица 6. Прогноз x1±5%

Дельта фактора	x 1 -5%	x 1 +0%	x 1 +5%
Реакция	1,16	1,17	1,109

Как видим, в таблицах значение фактора сокращается (который не подлежит управлению), то есть x 1 на 5% представляет собой наименее благоприятный вариант, что обусловлено снижением уровня развития на 1,98%.

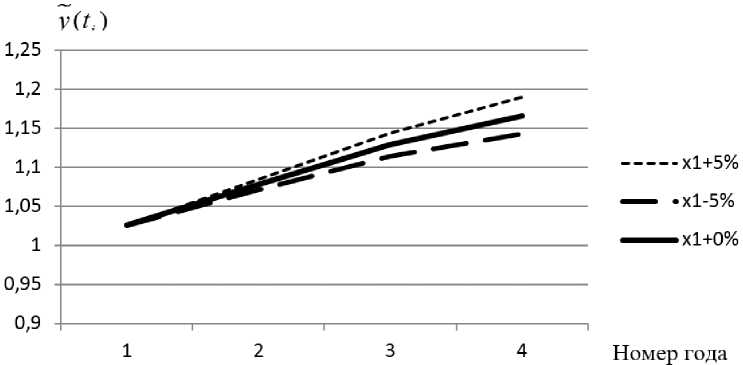
Рис. 2. Прогноз развития механизма с 2020 года по 2022 год при разных показателях x 1

Смена главного управляемого коэффициента ЛПР поможет провести анализ допустимого изменения отрицательного воздействия фактора на механизм. Сменим управляемый фактор (x 2 количество административного аппарата) на +5 процентов. Далее найдем размер оказываемого на гармоничное положение системы влияние, которое рассчитано по наиболее неблагоприятному сценарию, который не поддается управлению x 1 – 5% (таблица 7, рис. 3).

Таблица 7. Снижения влияния неблагоприятных факторов (не поддающие управлению), вероятный сценарий

	x 2 – 5%	x 2 + 0%	x 2 + 5%
x 1 – 5%	1,186546	1,17456	1,19787

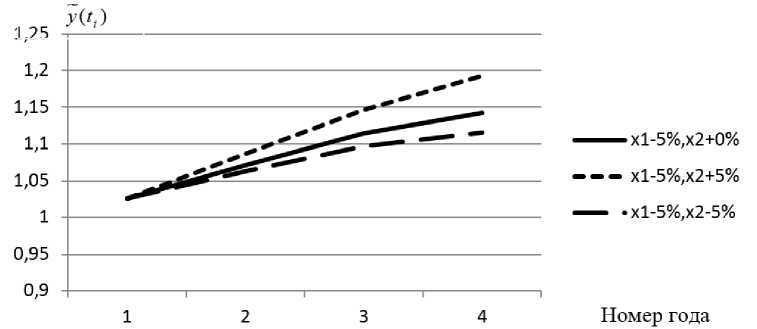
Рис. 3. Варианты значений при х 1 ± 5%

Заключение

Так, коррупция является особенно явной, проявляется она во всех отраслях деятельности современного постиндустриального общества. Уровень коррупционных преступлений постоянно имеет риск своего возрастания, это можно увидеть из данных официальной статистки Российской Федерации. Об этом говорят и данные расчетов, которые производятся при помощи математического моделирования. При позитивном развитии сценария, когда все отрицательные факторы перестанут сдавливать систему, то возможно, что рост коррумпированности будет постепенно снижаться. При развитии неуправляемых факторов настоящее положение системы может кардинально измениться.

Стоит также отметить, что активные действия и современные разработки противодействия коррупции относятся к различным категориям, таким как экономической, политической, психологической, социологической и юридической. Разработки в области математического моделирования позволят повлиять на ход борьбы с коррупцией в РФ.

Коррупция в корне меняет всю систему предложения и спроса в экономической области, оказывает негативное воздействие на социально-экономическое формирование инноваций, пытается исключить предпринимательскую активность и приводит к монополизации рынка. Поэтому противодействия коррупции помогут понизить размер ущерба и степень влияния на геополитическую конкурентоспособность и социально-экономическое развитие Российской Федерации.

Большинство математических моделей зачастую никак не сопоставляются со статистикой. Однако при помощи математического анализа можно намного эффективнее, точнее спрогнозировать ущерб, нанесенный коррупционными преступлениями.

Так проведя анализ в данной работе, можно сказать, что при отрицательном варианте развития неуправляемого фактора x 1 , что отражается в снижении электронных услуг на 5%, динамический размер снижения уровня преступлений, связанных с коррупцией, будет понижаться. Если же своевременно производить регулирование управляемого фактора x 2 , то данное положение вполне возможно исправить. При росте этого фактора на 5% динамика коррупции возрастет на 2,65 %, а если же произвести понижение x 2 , то динамика снизится на 2,4%. Но при повышении числа электронных услуг динамика снижения преступлений коррупционной направленности может, без учета регулирования фактора, поддающегося управлению, вырасти до значения равного 1,12%, что будет достигнуто без учета роста заработной платы административного аппарата в государстве.