Исследование возможности "захвата" начальной фазы колебаний передатчика генератором с жестким возбуждением методом имитационного моделирования

• 1.    Введение

  Среди удачных попыток сохранить преимущества некогерентных радиолокационных систем и в то же время сохранить качество обработки когерентного сигнала можно указать способ обработки пачки некогерентных импульсов, используемый в псевдокогерентных РЛС ( Финкельштейн , 1973). В этих системах применяется некогерентный зондирующий сигнал с запоминанием начальной фазы каждого излученного импульса, что позволяет при приеме отраженного сигнала исключить влияние случайной начальной фазы и сохранить только те фазовые сдвиги, которые происходят за счет движения цели. Запоминание начальной фазы осуществляют в аналоговом виде посредством стабильных опорных гармонических колебаний, заполняющих почти весь промежуток между импульсами, причем начальная фаза этим колебаниям навязывается каждый раз импульсом передатчика. Принятые сигналы сравнивают по фазе с опорным колебанием с помощью фазового детектора.

• 2.    Исследование возможности "захвата" начальной фазы колебаний передатчика генератором с жестким возбуждением

Проблема заключается в том, что получение опорного напряжения путем фазирования требует высокой стабильности частоты колебаний когерентного гетеродина. При этом точность фазирования тем выше, чем ниже добротность его контура, а для высокой стабильности требуется увеличение добротности пропорционально частоте генератора ( Дудлевич и др. , 1964).

Одним из способов решения данной проблемы может быть перевод когерентного гетеродина и фазового детектора на низкую промежуточную частоту и нахождение требуемой добротности колебательного контура гетеродина, при котором соблюдается точность фазирования и стабильность частоты колебаний.

Исследование возможности запоминания ("захвата") начальной фазы колебаний передатчика генератором с жестким возбуждением выполнено методом имитационного моделирования в приложении Simulink среды Matlab.

В ходе выполнения исследования был смоделирован генератор с жестким возбуждением (ГЖВ), осуществляющий запоминание начальной фазы передатчика в аналоговой форме. В имитационную модель также включены блоки формирования сигналов запуска и остановки ("гашения"). Функциональная схема ГЖВ, реализованная в имитационной модели показана на рис. 1.

Коммутационный блок 1 предназначен для пропускания импульса "гашения" генератора в момент окончания очередного такта локации. Блок 3 служит для непосредственной подстройки стабильного гетеродина на частоту тракта ПЧ.

При запуске генератора "пролезающим" импульсом, генератор возбуждается на частоте импульса с захватом фазы колебания и после прекращения воздействия запускающего импульса генерирует колебания на частоте собственного колебательного контура. Для доказательства возможности захвата частоты рассмотрим баланс фаз в автогенераторе под действием внешней ЭДС в предположении, что частота внешней ЭДС отлична от резонансной частоты контура. При этом амплитуду сигнала будем считать настолько малой, что все основные параметры автоколебания останутся такими же, как и в отсутствие внешнего воздействия. Иными словами, влияние внешнего воздействия проявляется только в изменении фазовых соотношений в автогенераторе.

Кривенко О.И. Исследование возможности "захвата" начальной фазы…

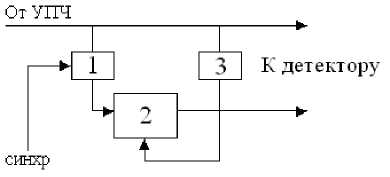
Рис. 1. Схема имитационной модели ГЖВ.

• 1    – коммутационный блок;

• 2    – стабильный гетеродин, настроенный на промежуточную частоту приемника;

• 3    – автоматическая подстройка частоты гетеродина

До включения источника внешней ЭДС эти соотношения характеризуются векторной диаграммой, показанной на рис. 2а. Ток I ₁ в фазе с напряжением U_БЭ = U_ОС , а напряжение U _K в фазе с током I ₁.

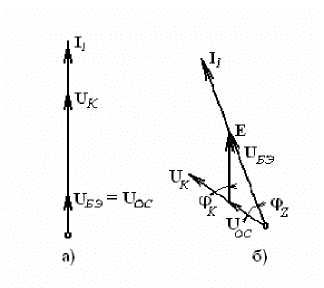
Рис. 2. Векторные диаграммы напряжений и тока в генераторе: а – без внешнего воздействия; б – в режиме захвата частоты

Исходная фаза тока I 1 выбрана произвольно, так как в автогенераторе фаза автоколебания зависит от начальных условий запуска. После включения внешней ЭДС e ( t ) = E cos ωt (начальная фаза θ приравнена нулю) и установления стационарного режима диаграмма примет вид, показанный на рис. 2б. При построении этой диаграммы учтены следующие условия:

• 1)    между током I ₁ и напряжением U _K имеется фазовый сдвиг φ Z , зависящий от расстройки контура по отношению к генерируемой частоте ω . Принимая для определенности, что ω < ω ρ , где ω_ρ – собственная частота резонансного контура, приходим к выводу, что вектор U _К должен опережать вектор I ₁ на угол

φ z = arctg [(2( ω – ω p ) Q )/ ω p ], (1) где Q – добротность контура;

• 2)    ток I ₁ находится в фазе с результирующим напряжением U _БЭ;

• 3)    напряжение обратной связи U_ОС , индуктивно связанное с напряжением контура U_K , не

зависит от частоты. Поэтому направления векторов U_ОС и U_К совпадают.

Из диаграммы видно, что нарушение фазового баланса автогенератора в коллекторной цепи на угол ϕZ (в сторону опережения) из-за расстройки колебательного контура (при ω < ωρ) компенсируется тем, что в цепи база – эмиттер результирующее напряжение UБЭ сдвинуто на угол φZ в сторону отставания относительно UОС.

Когда ω > ωρ, фазовый сдвиг в коллекторной цепи является запаздывающим, а в цепи база – эмиттер – опережающим.

Из условий 2) и 3), а также непосредственно из диаграммы на рис. 2б вытекает следующее равенство:

sin φ z = E (sin φ k / U БЭ ),                                         (2)

где ϕ К – фазовый сдвиг между Ε и U K .

Итак, если режим захватывания действительно существует, то одновременно выполняются равенства (1) и (2).

Используя оговоренное условие малости Ε по сравнению с UОС, можно считать UБЭ = UОС, sin φz = φz = (E/UБЭ) sin φk = (E/UОС) sin φk.

Малость угла φ z позволяет также и в выражении (1) заменить тангенс его аргументом:

tg φ z = φ z = 2( ω – ω p )( Q / ω p ).

Приравнивая правые части последних двух выражений, приходим к следующему важному соотношению:

2( ω – ω ρ )/ ω ρ = ( E / U OC ) sin φ κ (1/ Q ).                                     (3)

Из этого соотношения следует, что при заданной разности частот ω и ω Р сдвиг фазы напряжения U _K относительно синхронизирующего колебания равен ( Бойко и др. , 2004):

φ k = arcsin [{2( ω – ω p ) Q / ω p }/( E / U ОС )].

Следовательно, при совпадении частот ω и ω Р сдвиг фазы напряжения U К относительно синхронизирующего Е равен нулю. Имеет место захват фазы синхронизирующего колебания. После возбуждения генератор генерирует колебания с постоянной частотой и амплитудой в течение одного периода излучения импульса. После окончания периода необходимо предусмотреть "гашение" генератора, чтобы со следующим импульсом запустить его с нужной частотой и фазой.

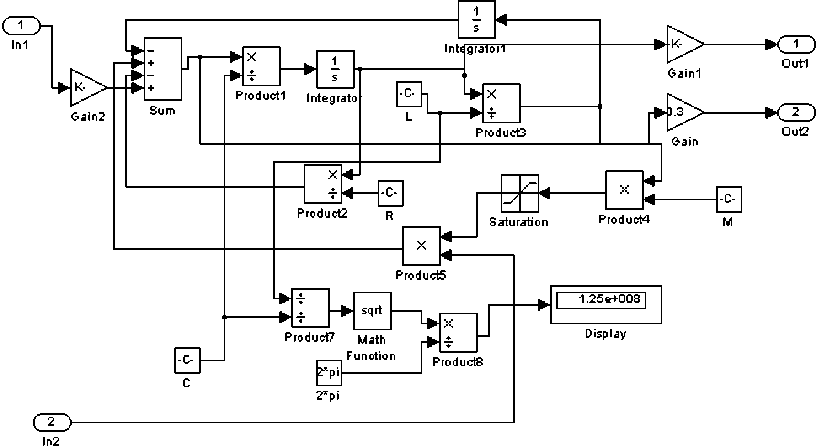
Рис. 3. Имитационная модель генератора с жестким возбуждением в среде Matlab

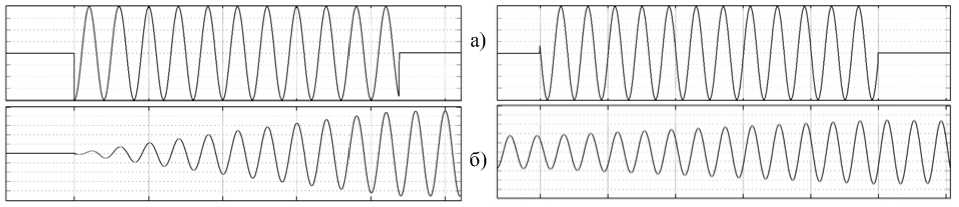
Рис. 4. "Захват" фазы ждущего генератора      Рис. 5. "Захват" фазы запущенного генератора

а) – "пролезающий" импульс; б) – собственные колебания ГЖВ

Теоретически факт "захвата" фазы синхронизирующего колебания вполне доказуем. Данный процесс можно исследовать на имитационной модели. На рис. 3 изображена блок-схема имитационной модели генератора со ждущим возбуждением. Схема имитационной модели полностью адекватна принципиальной электрической схеме генератора.

Вход 1 предназначен для запускающего импульса, вход 2 – для "гасящего", выход 1 – прямой, выход 2 – инверсный. На рис. 4 отображен процесс захвата фазы ГЖВ (б) "пролезающим" в тракт ПЧ импульсом (а), в случае заглушенного генератора. На рис. 5 изображен процесс "навязывания" начальной фазы работающему генератору.

3. Заключение

В условиях набирающей силу тенденции максимального приближения обработки сигналов к апертуре антенны цифровой подход для запоминания начальной фазы становится неприемлемым. В связи с этим продуктивным является путь поиска аналогового решения поставленной задачи и, как показывают исследования, такой путь вполне может быть найден. Следующим шагом данного исследования будет схемотехническая визуализация данного эксперимента, очевидно, представленная в программном пакете OrCAD 9.2. В лабораторных условиях сложно, дорого и нецелесообразно проводить исследования в твердотельном исполнении в то время как существуют столь мощные программные продукты. Однако при промышленном подходе к изготовлению модели нынешний уровень технологии вполне позволяет рассчитывать на высокую точность её реализации.