Исследование возникновения цикличности в экономических системах на основе построения модели однопродуктовой экономики

Для иллюстрациисущности и изучения неустойчивого равновесия экономических систем нами построенадинамическая модель однопродуктовой экономики, для которой характерны в период дискретного времени t ₀ начальная

непосредственно на его численность в

предшествующий момент времени t , а также на

условный агрегат

численность населения N ₀ и начальный запас

f1 - pF 1

V     R . )

задача которого

единственного ресурса

^R 0 .

Экономика

характеризуется ограниченным объемом мощностей

ресурсного воспроизводства

S.

Воспроизводство

численности населения описывается в модели с помощью коэффициента r .

Система дифференциальных уравнений (1) воспроизводит основные параметры динамики экономической системы.

<

dN

---= rN x 1

dt t

^^^^^^^е

pN )

V R )

dR

= Sh - N, p dt            ^t

где (выход

h – коэффициент воспроизводства ресурса ресурса в расчете на единицу мощности

ресурсного воспроизводства S );

p – коэффициент потребления ресурса (расход

ресурса в расчете на 1 чел. населения N_{t ).}

Если обратить внимание на уравнение, дифференциально описывающее движение численности населения экономической системы, то его логика базируется на произведении коэффициента воспроизводства численности населения r

ограничивать прирост населения в случае создания условий дефицита ресурса. Изменение ресурса прописано в модели с помощью разницы произведенного и потребленного ресурса в период

времени t .

Простота предложенной для иллюстрации интересующих нас процессов модели, безусловно, не соответствует условиям функционирования современной экономики, в особенности, ее однопродуктовость. Однако в полной мере модель

сохраняет основополагающие принципы экономической динамики, а в нашем узко прикладном аспекте – дает дополнительные преимущества за счет исключения усложняющих ее параметров.

В рамках имитации экономической системы присвоим исходные значения ряду переменных модели в довольно условном виде : N 0 = 100 ;

R0 = 100; S = 100; h = 0,8; p = 0,8.

На первом этапе введем в качестве начального условия нулевой коэффициент воспроизводства численности населения ( Г = 0 ). Система, находящаяся в равновесии, продолжает его сохранять на протяжении всего перспективного горизонта (рис. 1), а первоначальные параметры численности населения и объема ресурса остались неизменными.

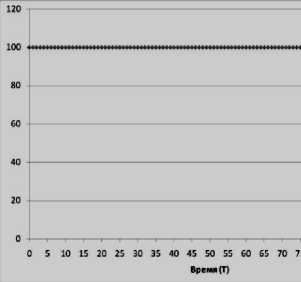
Рисунок 1 – Динамика численности населения N_t и объема ресурса R t (при h = p = 0,8 и Г = 0 )

На втором этапе увеличим реалистичность модели, приблизив ее к условиям существования человеческого    общества,    выраженным в биологическом инстинкте размножения популяции. Для этих целей примем коэффициент воспроизводства численности населения равным 0,05 (r = 0,05 ). Интерпретация данного коэффициента означает, что прирост численности населения в экономической системе в периоде t+1 по сравнению с периодом t составит 5%. Принимая во внимание, что объем мощностей ресурсного воспроизводства S ограничен, а выход ресурса в расчете на единицу мощности неизменен, с увеличением размера человеческой популяции объем доступного для потребления обществом ресурса начнет сокращаться, что приведет, в свою очередь, к сокращению численности населения, начиная с периода t, когда будет испытываться дефицит ресурса. Взаимообусловленная динамика производных dN и dt dR объясняет механизм цикличности (рис. 2) в dt изменениях численности населения и доступных ресурсах.

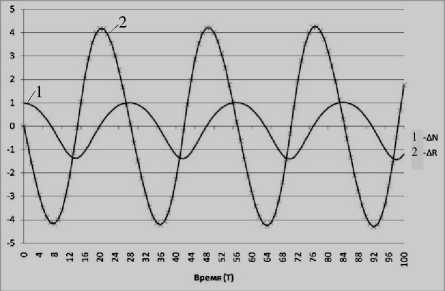
Рисунок 2 – Динамика изменения численности населения

AN t и объема ресурса AR t (при h = p = 0,8 и r = 0,05 )

Безусловно, данную модель можно сопоставить исторически разве что с периодом экономики первобытного общества по причине ее простоты. Тем не менее , благодаря ее характеристикам нам становится очевидна сущность всей экономической цикличности, лежащая в основе и современных экономических систем.

Если обратить внимание, на рисунок 3, на котором описаны состояния экономической системы при 5% приросте численности населения, то становится очевидной неустойчивость в равновесии экономических систем. Постоянные изменения численности нарушают пропорциональность между потребностями и ресурсами. Фактически с учетом целого ряда видоизменений и трансформаций причины цикличности неизменны и в современной экономике.

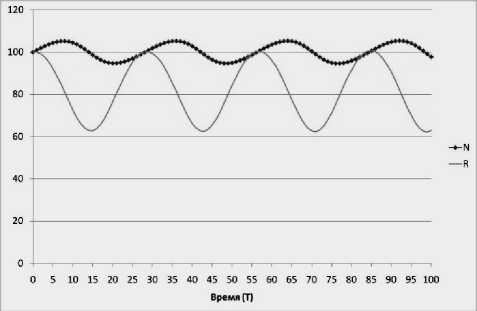
Рисунок 3 – Динамика численности населения N_t и объема ресурса R t (при h = p = 0,8 и Г = 0,05 )

Поведение системы, описанное на рис. 3, очень схоже с ситуацией мальтузианской ловушки, типичной и периодически повторяющейся для доиндустриальных обществ, в результате которой рост населения, в конечном счете, обгоняет рост производства продуктов питания (ресурса). Поэтому в долгосрочной перспективе не происходит ни роста производства продуктов питания на душу населения, ни улучшения условий существования подавляющего большинства населения, а напротив — оно остается на уровне, близком к уровню голодного выживания [1].

К настоящему времени большинству человеческих обществ удалось выйти из мальтузианской ловушки (исключение пока составляют некоторые общества третьего мира, прежде всего в Тропической Африке).

«Мальтузианской ловушкой» ( Malthusian trap ) это явление названо потому, что оно было впервые замечено и достаточно строго описано Томасом Робертом Мальтусом, известным английским демографом и экономистом в 1798 г. в своем классическом труде «О росте народонаселения» («Essay on the Principle of Population»). Он впервые обратил внимание на тот факт, что численность популяции растет по экспоненте (в геометрической прогрессии), в то время как производство продуктов питания растет со временем линейно (в арифметической прогрессии), из чего сделал справедливый вывод, что рано или поздно экспонента обязательно "обгонит" линейную функцию, и наступит голод [3].

На основании этих выводов Мальтус говорит о необходимости ввести ограничения на рождаемость, в особенности для беднейших слоев общества. Экономический пессимизм, следующий из прогнозов предложенной им модели, в основу которой положен анализ эмпирических данных о росте населения в американских колониях, Мальтус противопоставлял модным в начале IXX века оптимистическим идеям гуманистов: Ж ана - Ж ака Руссо, Уильяма Годвина и других, предсказывающих человечеству грядущее счастье и процветание. Можно говорить о том, что Мальтус был первым ученым-алармистом, который на основании результатов моделирования "бил тревогу" и предупреждал человечество об опасности следования развитию по используемым ранее сценариям прогресса [4].

Во второй половине 20 века такую алармистскую роль сыграли работы Римского клуба ( TheClubofRome ), и в первую очередь "модель глобального роста" Дж. Форрестера [1], который применил разработанную им методику моделирования на ЭВМ к мировой проблематике . Результаты исследования были опубликованы в книге «Мировая динамика» (1971), в ней говорилось, что дальнейшее развитие человечества на физически ограниченной планете Земля приведет к экологической катастрофе в 20-х годах следующего столетия [7].

С резкой критикой мальтузианства выступал К. Маркс [4], подчеркивая, что хотя между уровнем развития производительных сил и темпом роста народонаселения в различных общественноэкономических формациях нет точного соответствия, данные исторических наук свидетельствуют о детерминации роста народонаселения развитием способа производства. Так, в условиях относительно медленного развития, характерного для феодального способа развития производства и темпы прироста народонаселения, как правило, являются замедленными. Напротив, быстрое развитие капиталистического способа производства, основанного на машинной индустрии, стимулирует ускоренный рост народонаселения.

Маркс показал, что абстрактного закона населения не существует, что каждому общественному строю свойственны особые, имеющие исторический характер, законы населения. Однако, как мы можем судить, какими бы оскорбительными эпитетами Маркс не наделял мальтузианство, критика сосредоточена, главным образом, на неэтичных мерах ограничения численности эксплуатируемого класса, то есть выводах, сделанных Мальтусом, а не на самой модели.

Г.Ю. Ризниченко [4] отмечает, что обсуждению важности вывода Мальтуса для популяционной динамики Дарвин посвятил несколько страниц своего дневника, указывая, что поскольку ни одна популяция не размножается до бесконечности, должны существовать факторы, препятствующие такому неограниченному размножению. Среди этих факторов может быть нехватка ресурса (продовольствия), вызывающая конкуренцию внутри популяции за ресурс, хищничество, конкуренция c другими видами. Результатом является замедление скорости роста популяции и выход ее численности на стационарный уровень.

Положения теории Мальтуса нашли широкое отражение в математической модели Лотке -

Вольтерра, которая с 30-х годов ХХ столетия применяется в физике, химии, медицине, демографии и биологии. Эта модель обрисовывает в биологии численные взаимосвязи в классических системах «хищник – жертва».Модель Лотки – Вольтерра – модель межвидовой конкуренции, названная в честь её авторов, которые предложили модельные уравнения независимо друг от друга (Лотка, 1925; Вольтерра, 1926) [5].

В математической форме предложенная система имеет следующий вид:

dx ,     „ .

— = (a - ву) dt dy                ,

— = (-у + Sx ) у

I dt

где x - количество жертв ;

• y - количество хищников ;

• t - время ;

• a ,    в , у и S - коэффициенты , отражающие взаимодействия между видами .

Рассматриваемая         нами         система дифференциальных уравнений (1) модели однопродуктовой экономики при некоторых допущениях вполне вписывается в параметры классической системы Лотки - Вольтерра «хищник-жертва» (2), что становится предпосылкой для модернизации изучаемой модели.

Применительно к доиндустриальным обществам теория Мальтуса продемонстрировала свою высокую объясняющую способность , однако для эффективного объяснения динамики современных обществ она нуждается в самых серьёзных модификациях . Мальтус не учел влияния НТП на развитие производительных сил и производственных отношений , выразившееся в увеличении доступных для общества продуктов .

Конструктивная составляющая критики К . Маркса в отношении мальтузианства подчеркивала именно игнорирование темпов роста производительности труда , как результата НТП , которые росли с переходом на каждую новую социально экономическую формацию . В связи с логикой данных рассуждений рассматриваемая нами модель была расширена НТП - составляющей – показателем скорости роста коэффициента воспроизводства ресурса ( v_h ), который представляет собой отношение выхода ресурса в расчете на единицу мощности ресурсного воспроизводства в каждом последующем периоде по отношению к предыдущему :

h vh = 4+1.            (3)

ht

На этом этапе исследования мы позволили себе в модели величину vh не менять на протяжении всего моделируемого ряда динамики. Мы пошли на данное допущение, между тем, сознавая, что в исторической действительности развитие производительных сил и производственных отношений протекает с определенным ускорением. К моделированию ускорения НТП вернемся на следующих этапах, а пока обратим внимание, на изменение динамики системы с вводом дополнительного параметра научно-технического прогресса vh . Система приняла следующий вид:

dN

= rNt x dt pN,)

.

R , )

dR

= Sh t v h ^- N , p , dt

Введем допущение, при котором v h = 0,01, что означает 1% прирост выхода ресурса в расчете на единицу мощности ресурсного воспроизводства ( S )в каждом последующем периоде , ₊ 1 по отношению к предыдущему t . Исследование динамики изменения численности населения AN_t и объема ресурса AR_t (рис. 4) дает понимание о сохранении цикличных колебаний в экономической системе.

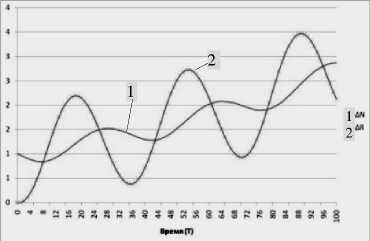
Рисунок 4 – Динамика изменения численности населения ^N t и объема ресурса AR , (при h = p = 0,8 ; r = 0,05 ; v h = 0,01)

Однако характер изменений численности населения и объема ресурса уже носит по сравнению с моделью без влияния фактора НТП свойство возрастания с изменением времени.

Примечательно, что экономика демонстрирует устойчивый рост с течением времени t , выражающийся в увеличении численности населения и объема ресурса для удовлетворения его потребностей (рис. 5).

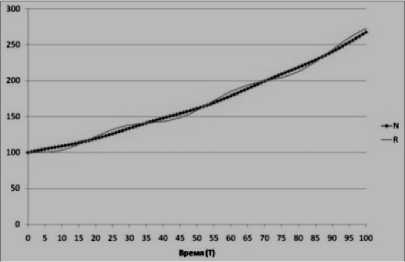
Рисунок 5 – Динамика численности населения N_t и объема ресурса R_t (при h = p = 0,8 ; Г = 0,05 ; v h = 0,01 )

Построенные фазовые портреты траекторий изменения численности населения и объема ресурсов в координатах времени t и t + 1 (рис. 6) отражают затухание колебаний в системе под воздействием научно-технического прогресса, что позволяет говорить о приобретенной динамической устойчивости системы. Интерпретируя на повседневный язык полученные результаты, мы можем провести аналогию с ездой на велосипеде . До тех пор, пока крутятся педали, велосипедист может не опасаться падения. Точно так и в рамках изучаемой однопродуктовой экономики – пока действует НТП, система пребывает в состоянии динамической устойчивости, которое позволяет восстанавливать теряемое стационарном состоянии равновесие . Неслучайно, устойчивость экономики связывают именно с экономическим ростом, который в условиях ограниченности ресурсов следует связывать только с фактором научно-технического прогресса.

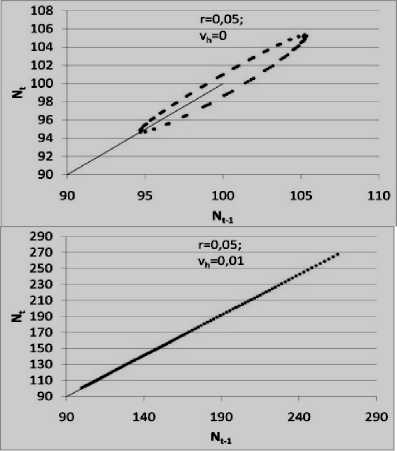
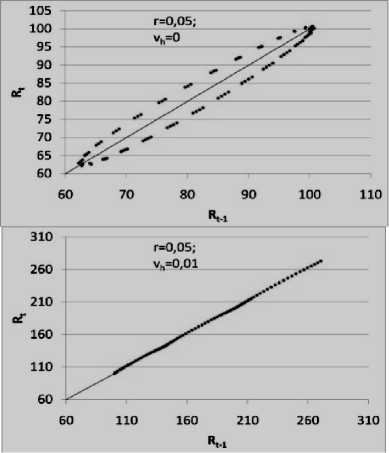
Рисунок 6 – Фазовые портреты траекторий изменения численности населения и объема ресурсов в координатах времени t и t + 1

Снижение амплитуды колебаний связано с нормализацией показателя ресурсообеспеченности (R/N), который определяется как средний объем ресурса в расчете на каждого индивидуума общества (рис. 7б). В то же время, на рис. 7а отражена динамика увеличивающихся колебаний ресурсообеспеченности, что свидетельствует о наступлении некоторого момента времени t , когда уровень обеспеченности ресурсом индивидуумов в экономике достигнет минимально критического уровня, что,в конечном счете, приведет к гибели всего населения в условиях отсутствия НТП. Ведь для субъектов экономики индивидуальная угроза цикличности заключается именно в кризисных явлениях, и именно НТП является фактором снижения колебательных процессов. Таким образом, научно-технический прогресс индуцирован потребностью общества вернуть равновесие в экономическую систему, а никак не наоборот.

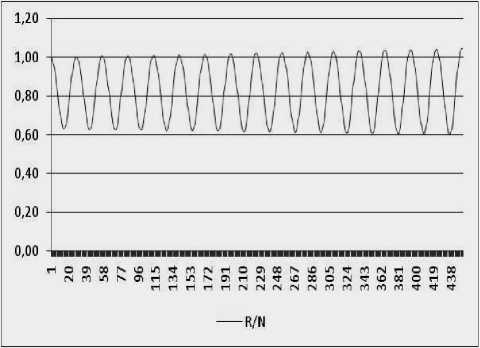
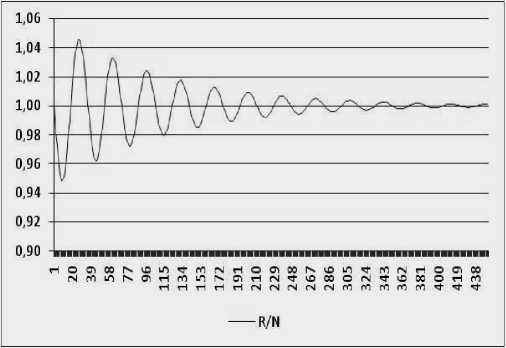
а) v h = 0

б) vh = 0,01

Рисунок 7 – Динамика колебаний показателя ресурсообеспеченности ( R/N ): а) при отсутствии фактора НТП; б) при воздействии НТП

Фазовые портреты изменения доступного для потребления объема ресурса в координатах ресурсообеспеченности и темпа прироста запасов (рис. 8) свидетельствуют, что введенный нами в модель однопродуктовой экономики фактор НТП позволяет вывести систему на новый устойчивый аттрактор, чего не удается сделать в отсутствии НТП . На рис. 8а видно, что траектория движения направлена наружу от центра устойчивого состояния с увеличением радиуса, а на рис. 8б – демонстрируется обратное движение к достижению аттрактора – в центр спирали.

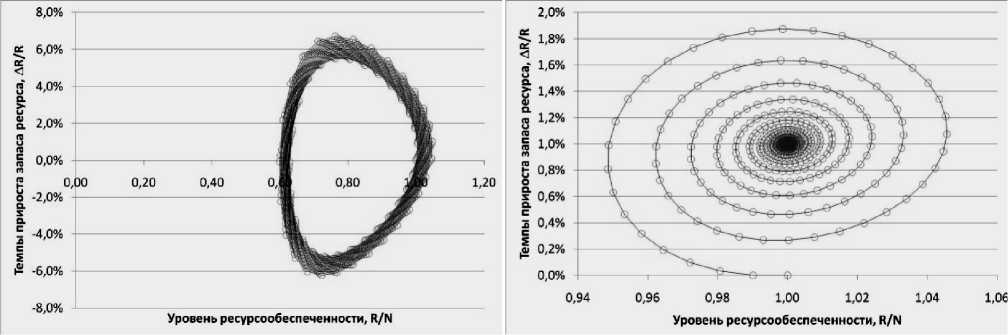
а) v_h = 0

• б)    v h = 0,01

Рисунок 8 – Фазовые портреты траектории изменения доступного для потребления объема ресурса в однопродуктовой экономике в координатах ресурсообеспеченности и темпа прироста запасов а) при отсутствии фактора НТП ; б) при воздействии НТП

Исследуя закономерности в траекториях однопродуктовой экономики, мы проследили ее поведение при изменении коэффициента воспроизводства численности населения r от 0,1 до 0,4 при отсутствии фактора НТП ( v_h = 0 ) (рис. 9).

Данное наблюдение позволило установить, что с ростом значений r частота и амплитуда циклических колебаний усиливалась, что дает основание полагать о снижении устойчивости при увеличении темпов расширения популяции.

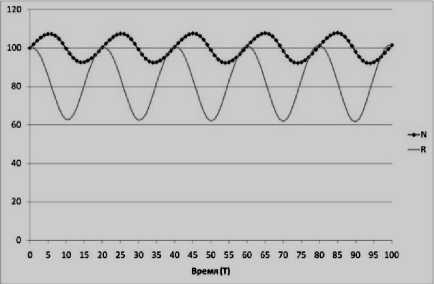
r = 0,1

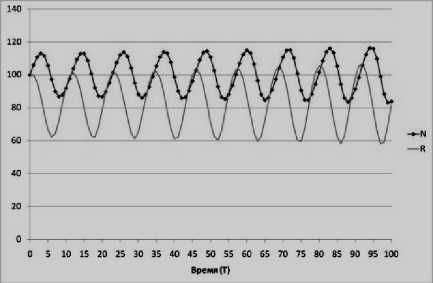
r = 0,3

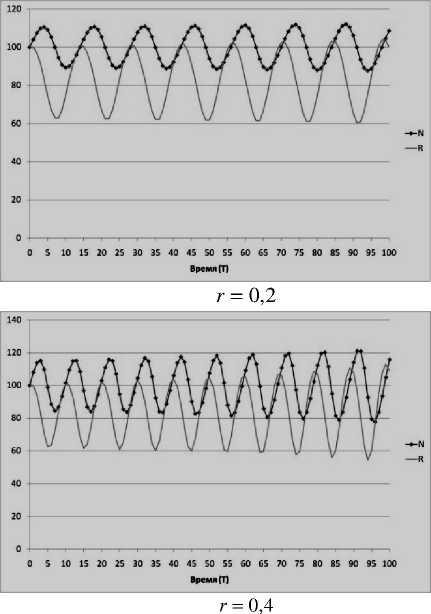
Рисунок 9 – Динамика численности населения N_t и объема ресурса R_t при различных значениях r

В данном случае мы рассматриваем фактор экстенсивного роста потребностей общества за счет увеличения численности его индивидуумов. Однако в реальных экономических системах, в особенности, современных, наблюдается сокращение численности населения при росте совокупного объема потребностей.

Для анализа воспользуемся пирамидой потребностей, разработанной А. Маслоу (рис. 10).

Развитие производительных сил ведет к тому, что достигается увеличение количественного потребления на душу населения, когда превышается некий условный уровень, то появляются новые потребности уже более высокого уровня (движение от основания пирамиды вверх). Их реализация формирует новую систему ценностей и, в конечном счете, переориентирует спрос на новые товары (ресурсы).

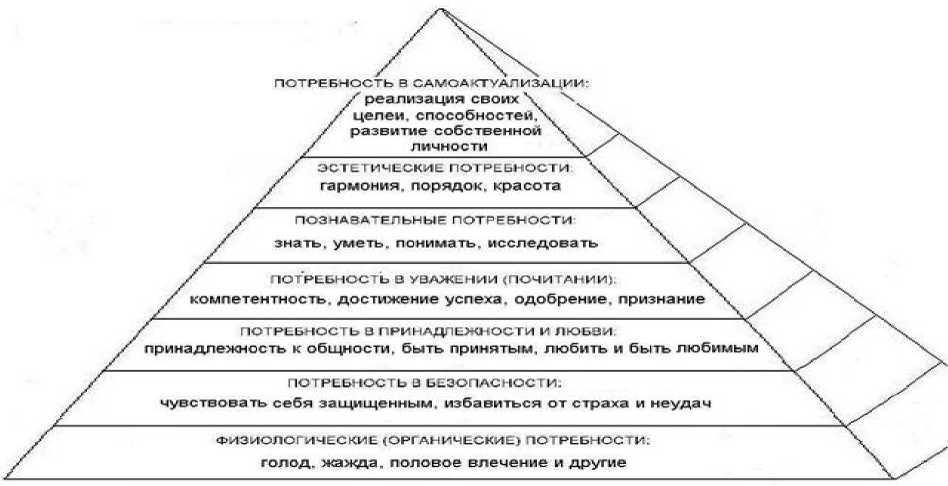
Рисунок 10 – Пирамида потребностей (А. Маслоу)

Попробуем в рамках модели однопродуктовой экономики сделать допущение, позволяющее считать, что отсутствует верхняя граница потребления ресурса индивидуумом. Это обусловлена тем, что в рамках многопродуктовой модели потребление ресурса по достижению определенного уровня насыщения переходит к другому. В однопродуктовой же модели будем считать, что рост потребностей нелимитирован ничем, кроме скорости изменения коэффициента потребления ресурса (vp ), который представляет собой отношение объема потребления ресурса отдельным индивидуумом общества в каждом последующем предыдущему:

vp периоде по отношению к

pt

При этом модель принимает следующий вид (рис. 11):

dN = rN x f l - N J dt t I R J .

dR = Shv - Np dt

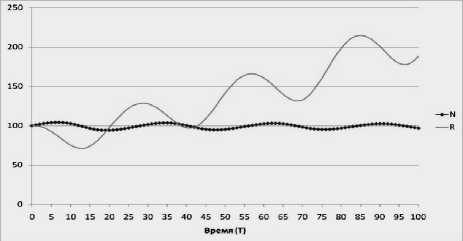
Рисунок 11 – Динамика численности населения N_t и объема ресурса R_t (при h = p = 0,8 ; r = 0,05 ; v h = v _p = 0,01 )

Цикличность, как имманентное свойство экономических систем, будет сопровождать их на любом этапе развития, поскольку в основе формирования диспропорций между потребностями и ресурсами лежит социально-биологическая природа существования человечества.