Исследование вынужденных колебаний линейной системы с двумя степенями свободы и малым параметром методом Ляпунова-Шмидта

В работе [5] приведено исследование периодических решений одной линейной неоднородной системы второго порядка с малым линейным возмущением. В работе [6] проведено исследование вынужденных колебаний одной линейной системы двух связанных осцилляторов с малым параметром.

В настоящей работе исследуются вынужденные колебания линейной системы с двумя степенями свободы и малым параметром при условии, что на систему действует внешняя периодическая сила с двумя соизмеримыми частотами.

Математическая модель вынужденных колебаний системы с двумя степенями свободы и малым параметром. Рассмотрим математическую модель вынужденных колебания системы с двумя степенями свободы в виде [7]

(? i +n 2 Q i -KQ₂ = FM, I Q 2 +n²₂Q₂-KQ i = F₂(t),

где n2 и n2 — парциальные частоты, К > 0, функции Fi(t) и F2(t) имеют вид Fi(t) = Гц sin(wit + би) + т-12 sin(w2t +

F1(t) = Г21 sin(^it + 021) + Г22 sin(«2t + где rks, 0ks, шк £ R, k,s = 1, 2, ш2 = аы±, a £ Z. Обозначим T = —.

S

Исследуем вынужденные колебания системы (1), когда параметры системы мало отклоняются от заданных значений и две частоты вынужденных колебаний совпадают с двумя частотами собственных колебаний (случай резонанса). В этом случае, система (1) с учетом малого параметра будет иметь вид fQi + (n1 + £dn)qi + (—K+sdi2)q2 = Fi(t), I q2 + (-K + Edn^qi + (n1+ed12)q1 = F2(t),

Где d_ks £ R, k,s = 1,2, e - малый вещественный параметр. Заметим, что система (1)

получается из системы (3), если положить E = 0.

Сформулируем задачу для системы (3): при достаточно малых вещественных E найти

T -периодическое решение q_i(t,E), q₂(t,E) системы (3), удовлетворяющее условию q_i(t,0) = Q_i(t), q₂(t,0~) = Q₂(t), где Q_i(t), Q₂(t) есть T -периодическое решение системы (1).

Периодичность решения Q_i(t), Q₂(t) системы (1) достигается за счет подбора амплитуд r_ks и начальных фаз 0 k _S в формуле (2) для периодических функций F_i(t) и F₂(t).

Представление математической модели в виде системы обыкновенных дифференциальных уравнений в нормальной форме. Делая в системе (3) замену

X i = q i , X 2 = q i => X i = X 2 ,

X3 = q2, X4 = q2 => X3 = X4, получим систему обыкновенных дифференциальных уравнений в нормальной форме dx

~7~ = (Bq — EBi)x — f (t), dt где х £ R4,

b„ = (

0 —n i 0 К

0 К

—n 2

0 ^di,i 0 ^d2,i

0 ^di,2 0 ^d2,2

'f^'"'}

J     ——FM/

Системе (1) соответствует неоднородная линейная система обыкновенных дифференциальных уравнений в нормальной форме dz

-^ = B_oz-f ⁽ t)

В этом случае задача, сформулированная для систем (1) и (3), перейдет в задачу для систем (5) и (6) в следующем виде: при достаточно малых вещественных г найти T —периодическое решение x(t,E) системы (5), удовлетворяющее условию x(t, 0) = z(t), где z(t) является T —периодическим решением системы (6).

В дальнейшем систему (5) будем называть возмущенной системой, а систему (6) – невозмущенной.

Вычисление периодического решения возмущенной системы методом Ляпунова-Шмидта. В работе [1] приведено решение поставленной задачи методом Ляпунова-Шмидта. Периодическое решение возмущенной системы будем вычислять с помощью разработанного на основе метода Ляпунова-Шмидта алгоритма в математическом пакете Maple.

Для иллюстрации разработанного алгоритма в пакете Maple выберем параметры системы (5) следующим образом:

^ 1 — 3, ^ 2 — 9, ^ 1 — ^2 — 45, К — 36, du —  2, d 22 — 2, d i2 — d2i — 0.

Собственные значения матрицы В₀ при выбранных значениях параметров равны Л 1, ₂ — ±3i,     Х₃ ,4 — ±91.

Поскольку для системы (6) частоты собственных колебаний совпадают с частотами вынужденных колебаний, то для система (6), а значит и системы (1) имеет место случай резонанса. В этом случае Г — -П и задача сводится к нахождению 2П —периодического решения системы (5).

Вычислим обобщенный жорданов набор оператора dx Ъо—Вох-А-dt по формулам

Во^ — 0, ®0^П — В^'Л                   (7)

где j = 2, р_к, к — Си .

Согласно методу Эйлера, решения уравнений (7), будем искать в виде

Vk ) — и^е^,                                    ⁽⁸⁾

где Х.Е R, и(р Е R 4 .

Подставляя формулы (8) в уравнения (7), получим следующие элементы обобщенных жордановых цепочек оператора В₀

^i1)^^) = el3t

"3^

1 l

— \17

( l \ " 54

4s I,

0 /

-

^ ⁽¹⁾ (t) = e^l9t

А 1

—

/ "—\

I     1 ⁶ 2 I

, <р2 ^{2) (}о = ^{е 1}И 18

0 0

.

Здесь число и длины жордановых цепочек равны п = 2, р 1 = р₂ = 2, соответственно.

Элементы обобщенных жордановых цепочек сопряженного оператора  30, удовлетворяющих условию биортогонализации, имеют вид

^ ⁽¹⁾ = e^3lt

,

^ ⁽¹⁾ = e ^9lt

Коэффициенты c_k j в разложении искомого периодического решения вычислим по

формулам

T ckj = W,^^ = ^ J (fW'Vk^tydt, 0

k,j = 1,2 .

Учитывая формулы (11) и (12), получим

27r 11 e^iS11  1 27r₁₂e

iS12

,

^С 12 =

3^ 12 6

,

81г₂₁е^1в 21

^c21 =     2

-

81г₂₂е^1в 22

,

9r₂₂e^ie 22

c?2 =--;----

²²          4

.

Для того, чтобы система (6) имела

T -периодическое решение, необходимо и

достаточно, чтобы c ,, = 0 и c₂₁ = 0 [1],

что эквивалентно следующим условиям,

соответственно,

^r₁₁e ^l0 1 ¹ + r₁₂e ^ie 12 = 0, r₂₁e^ie 21 —r₂₂e^ie 22 = 0.

Решения уравнений (14) и (15) можно записать в параметрической форме, соответственно,

711 = 712 = 71, 011 = 01 012 = 01 + ^, r21 = r22 = r2, $21 = $2 $22 = $2, где ’к, $к, к = 1,2, - произвольные вещественные параметры.

После подстановки формул (16) и (17) в выражения (13), получим „            3r₁e^1S1            _п             9r₂e¹⁰²

^С11 = °,  ^С 12 =    7    ,  ^С 21 = °, ^С 22 =       7   .

4                              4

Тогда при г ^ 0 вычисляя величины ^_к по формулам (3.3) из работы [1], получим 3r₁e ^{t0 1}              9r_?e¹⁰²

^ 1 =“' ^{? 2} =4Т

Дополнительное слагаемое у(г), входящее в -L —периодическое решение системы (5)

и принадлежащие к дополнению корневого пространства, имеет вид

y(t, г) =

( ^— MF+M’^¹¹¹^ ⁺ $ ■ '  318 2 ‘б’^{? n 9}' ⁺ $ 2 ))

^— 128^{г +} 12 ^r 1 ^{Cos (3t +} $ 1 ) ^{— (}4!^г—■ 1) ’ 2 ^{C0S (9t +} $ 2 ) -2Р²—2’ 1 ^S1n(3t + $ 1 ) + _2г 2 ^г_— 2 ^r 2 ^{S1n (9t +} $ 2 ) — 223—2r 1 cos⁽3^f + $ 1 ) + 2Р⁹—2’ 2^ (9t + $ 2 )

—

—

—

—

—

—

—

—

.

\

/

Таким образом, подставляя формулы (9), (10), (18) и (19) в выражение (3.4) из работы

[1], получим -L - периодическое решение системы (5)

x(t, г) =

I — ^r 1 sin(3t + $ 1 )

— — r 1 cos⁽3t + $ 1 )

2г         _

—

—

— r 2 Sin(9t + $ 2 ) \

;9-r 2 COS⁽9t + $ 2 ) ²1^г        .        ..

.

—

\—

— r 1 s1n(3t + $ 1 ) + —T 2 sin(9t + $ 2 ) r 1 cos(3t + $ 1 ) + ^r 2 cos(9t + $ 2 ) /

2г                  2г               '

Построение графиков компонент периодического решения и фазовых траекторий системы (3). Учитывая замену (4) из формулу (21), получим qi(t, г) = — ^r sin(3t + ej —-^^ш^С + $2), 2г                2г q2(t,г) = — 71r1s1n(3t + $1) +;1r2s1n(9t + $2). 2г                2г

Для построения графиков компонент решений и фазовых траекторий системы (3) выберем следующие наборы параметров:

1) ’ 1 = 0,5; ’ 2 = 0,3; $ 1 = 0; $ 2 = 0;

• 2)    ’ = 0,5; r₂ = 0,3; $_г = 0; $₂

• 3)    ’ = 0,5; r₂ = 0,3; $_г = 0; $₂

2L 5'

4n

I

;

.

решения и фазовых траекторий системы (3) при различных значениях параметра г.

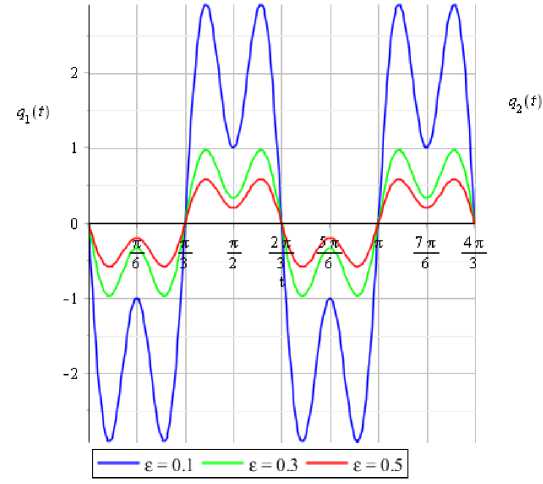
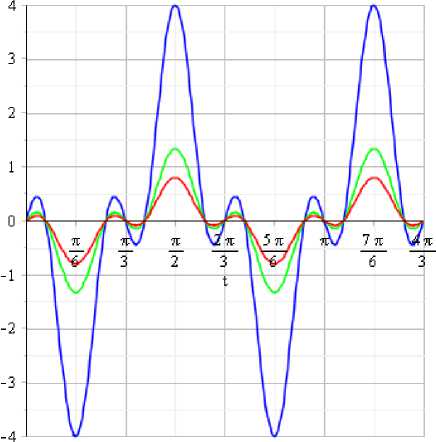
-----£ = 0.1 -----£ = 0.3-----£ = 0.5

а) q i (t^)                                          б) ? 2 (t, г).

Рис. 1. Графики компонент а) q 1 (t, г) и б) q₂(t, г) 2^ — периодического решения

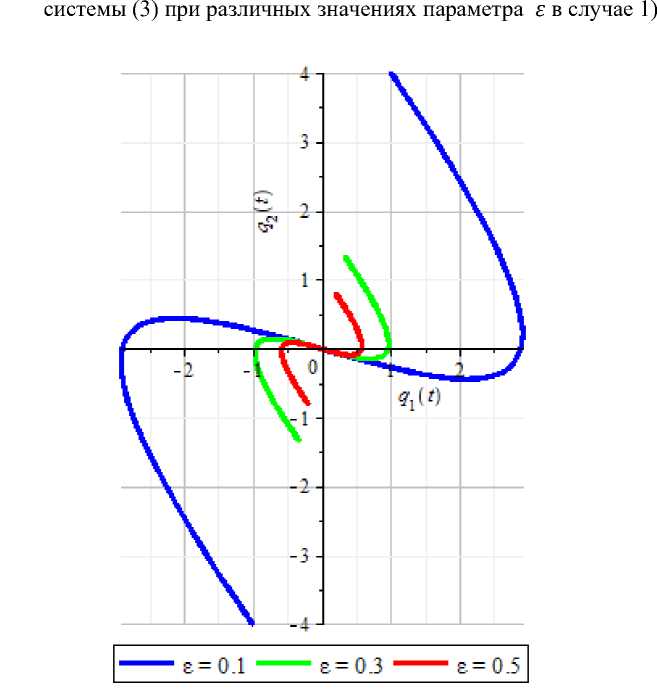
Рис. 2. График фазовой траектории системы (3)

в конфигурационном пространстве Oq 1 q₂ при различных г в случае 1).

решения и фазовых траекторий системы (3) при различных значениях параметра г.

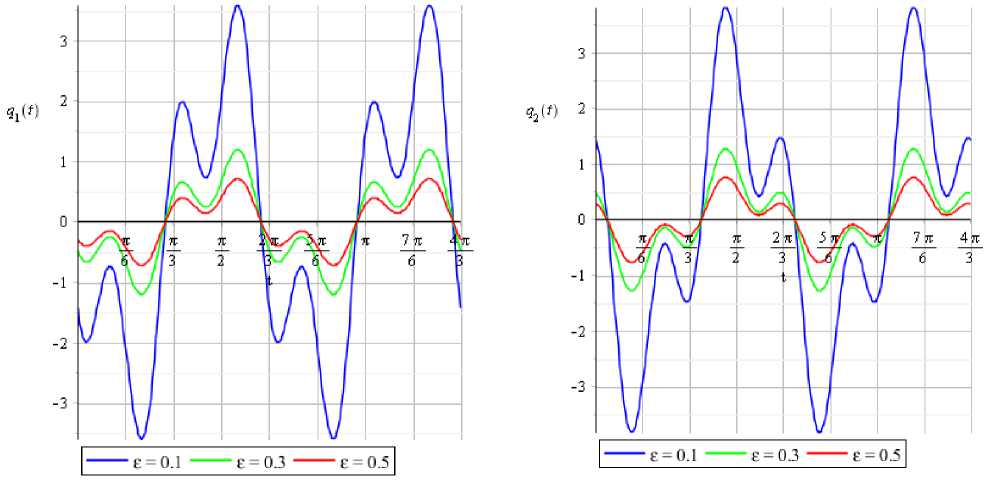
а) q^t^;                                    б) q 2 (t,г').

Рис. 3. Графики компонент а) q 1 (t, г) и б) q₂(t, г) 2^ — периодического решения системы (3) при различных значениях параметра г в случае 2).

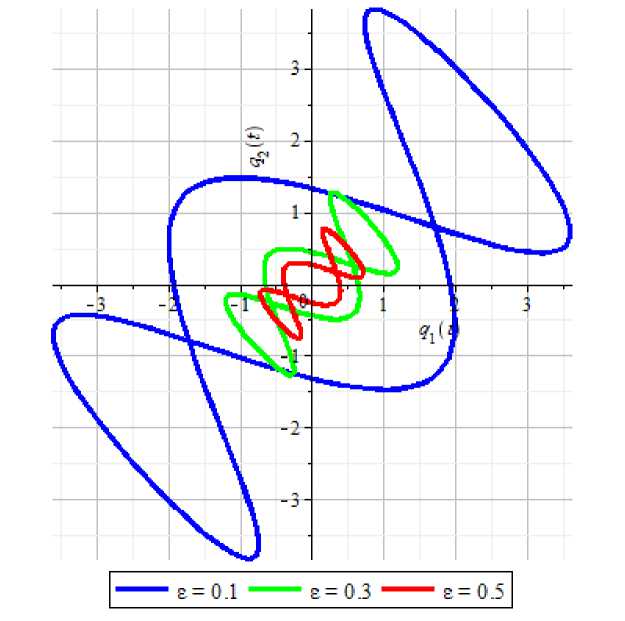
Рис. 4. График фазовой траектории системы (3)

в конфигурационном пространстве Oq 1 q₂ при различных г в случае 2).

решения и фазовых траекторий системы (3) при различных значениях параметра г.

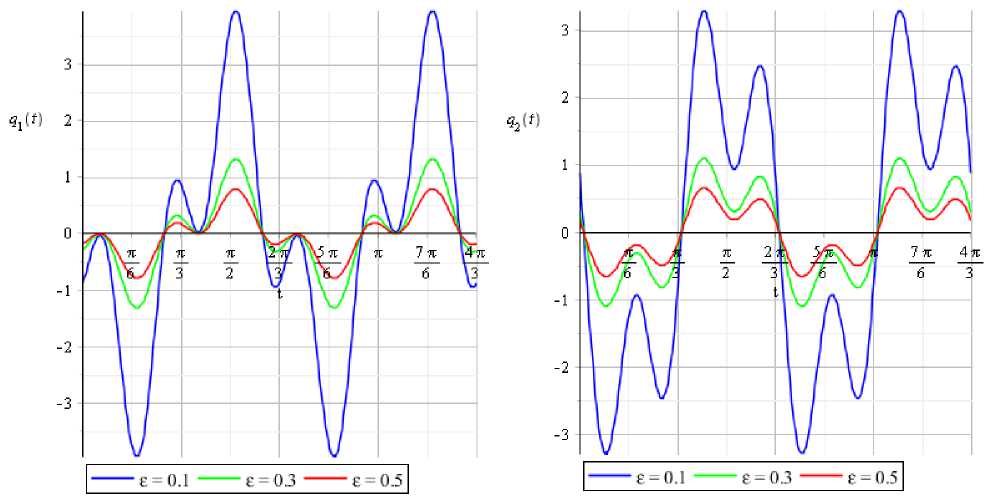
а) q^t^;                                    б) q 2 (t,г').

Рис. 5. Графики компонент а) q 1 (t, г) и б) q₂(t, г) 2^ — периодического решения системы (3) при различных значениях параметра г в случае 3).

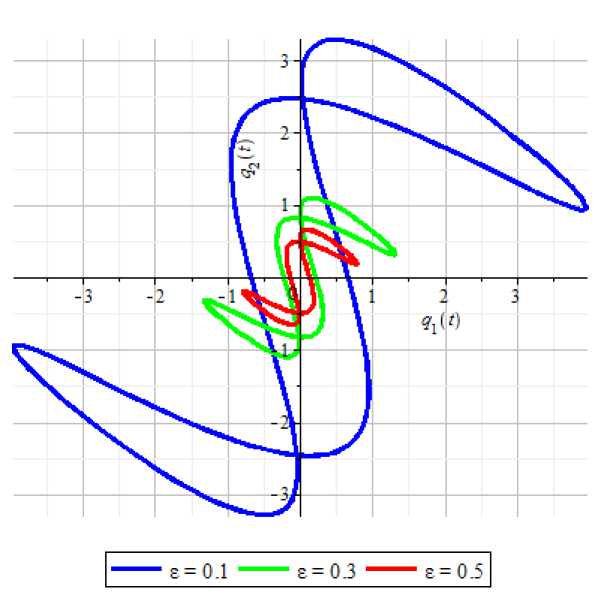
Рис. 6. График фазовой траектории системы ( 3)

в конфигурационном пространстве Oq 1 q₂ при различных г в случае 3).

Заключение. Из формулы (21) следует, что каждая компонента —— периодического решения системы (3) имеют полюс первого порядка в точке £ = 0 и зависит от тех же начальных фаз 6_ks и амплитуд r_ks, что и периодические функции F^t) и F_—(t).