Математическая модель системы двух связанных осцилляторов с малым параметром. Рассмотрим математическую модель вынужденных колебаний двух связанных осцилляторов [7] с малым параметром т^ + (Сц + гd11)q1 + (С12 + гd12)q2 = F^t),

n^h + (С12 + sd12)q1 + (С22 + гd22)q2 = F2(t), где q1 и q2 - обобщенные координаты системы двух связанных осцилляторов; г - малый вещественный параметр; F1(t), F2(t) - внешние силы, изменяющиеся по закону

F1(t) = r1 sin(wt + 91),  F2(t)=r2 sin(wt + 92), здесь r1> 0, r2 > 0, 91, 92, ш E R.

Будем предполагать, что для параметров т^ С^, dij E R, i < j, i,j = 1,2, системы (1) и достаточно малого г справедливы неравенства mi > 0, Си + гСц > 0, (Сц + гСц)^ + гd22') - (С12 + гС^)2 > 0.

Выполняя замену координат

(х1 {х з

= q 1 f = q 2 ^i

х 2 = х 1 = q 1 . х 4 = х з = q2 ’

в системе (1), запишем ее в векторной форме

Сх

А-Г = (8о — гВ1)х- f(t), dt где х = со1оп(х1,х2,х3,х4),

А =

I 0 т1  0   0 \      R|

I 0  0  10 1’    В0I

\0   0   0 т2/\

m 2

^С 12

-1 0

0 0

^С 12

^С 22

-0’}

В 1 = (

0 ^d 11 0 ^d 12

0 ^d 1,2 0 ^d 22

),   f(t) = J^r1i,n^

/               \Г2 sin(ut + 92)/

2 sin(^t

На основании результатов работы [5] исследуем вынужденные колебания системы (2) в математическом пакете Maple при следующих значениях параметров т1 = т2 = 1,    С11 = С22 = 5,    С12 = 4,    d11 = —2, d22 = 2,    d12 = 0.

При выбранных значениях параметров матрица В0  имеет следующие собственные значения

2 1,2 = ±ⁱ,      ^ 3,4 = ±³ⁱ.

Тогда возможны два случая возникновения резонанса: 1) ы = 1; 2) ы = 3.

Следовательно, согласно [5], в случае 1) Т = 2п, а 1 = 1, а₂ = 3, а в случае 2) Т = ^—р, а 1 = 3.

Ставится задача [1]: при достаточно малых вещественных г найти Т-периодические решения x(t,s) уравнения (2), удовлетворяющее условию x(t,0)=z(t), где z(t) является Т -периодическим решением уравнения

A^d_t=B „ z-fm.

–

В дальнейшем систему (2) будем называть возмущенной системой, а систему (3) невозмущенной системой.

Обобщенные жордановы наборы, удовлетворяющие условию биортогональности.

Элементы фР, ф Р , к = 1,п, j = 1,P^s обобщенных жордановых цепочек оператора

d

B0 = B0-A- и его сопряженного

d

B* = B*+A*- определяются по формулам [5]

В_оф р = 0,

В ^ ф¹ = 0,

В^ = В^-Р в^К = ВФ^. k,s = 1,п,

,

j = 2,Pk, l=2SPS,

где B l - матрица, сопряженная к В 1 .

Полагая

Ф Р = ppe ^- ,   ф р

= Upe^,

где фр, и^ Е С^ из формул (4) вычислим

• 1)    в случае ы = 1: п = 2, р 1 = р₂ = 2,

  Ф⁽¹⁾ = e^3lt

  
  

  IР

  -1

  
  

  , ф^2- = e^3lt

  
  

  (—6} — -2 vJ

  
  

  , y - ¹ =e^l

  
  
  

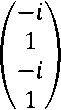
  , yf² = e^l

  
  

  ( -^ 2 W

  
  

  ,

  
  

  РЗ = e^3lt ( 3Pi² = e^3lt

  
  

  —2

  
  

  , ^⁽⁽¹⁾=e^l ‘ ([)

  
  

  ,  p ^ ²^ = e^lt

  
  

  = e

  
  

  ^— 2 UI

  
  

• 2)    в случае w = 3: п = 1, p 1 = 2,

  р⁽¹⁾ = e^3lt

  
  

  (ц

  ^—1

  
  

  , ( 1 ²⁾ = e^3lt

  
  

  IA

  
  

  —

  
  

  2 . ^p( = e^3U

  
  
  
  

  (!)

  
  

  , p⁽²⁾ = e^3it

  
  

  — 2 Vi)

  
  

  .

  
  

Непосредственной проверкой убеждаемся, что обобщенные жордановы наборы в случаях 1) и 2) удовлетворяют условиям биортогональности [5]

« Zk^? »= S ks S ji , ₇(^j) — п ,А Р к+ ^- ~Г1

Zk  = B1(k      '

« (kkrP »= Sksfy.

j = 2,pk,     l = 2,ps, где  3ks , 3ji - символы Кронекера,

«^.p1»^^^^ 0

yY = B^™ k,s = 1,п.

«(№

,

т

»=^/ (pk^.Y^tyidt,

где <•;> - скалярное произведение векторов.

Нахождение коэффициентов в разложении искомого обобщенному жорданову набору. Согласно [5] вычислим периодического решения возмущенной системы по формуле т периодического решения по коэффициенты в разложении

9kj = «f,Pkj)>^ = 1/ (f(t),ipkJ\t))dt, к = 1,п, j = 1,pk . 0

Заметим, что для того, чтобы невозмущенная система (3) имела T -периодические решения необходимо и достаточно, чтобы 9 k1 = 0, к = 1,п.

Рассмотрим случай 1) w = 1. Имеем

911 = 0 .     912 = °,

921 = i(—r1ele1 + r2eie2),

_ 1 ^22 = 4.

Если —г^^¹ + r₂e^² = 0, то 9₂₁ = 0 и система (3) имеет семейство 2тт-периодических решений. В частности, это условие выполняется при r 1 = r₂ = 1 и 6 1 = 6₂ = \

Рассмотрим случай 2) w = 3. Имеем

3 11 = 3i(r 1 e^ld1 +r 2 e^l02), g^ =—^-

Если (r1eie1 + r2eie2) = 0, то g11 = 0 и система (3) имеет семейство -^--периодических решений. Это условие выполняется, например, при r1 = r2 = 1, 01 = 0 и 62 = п.

Нахождение дополнительного линейного слагаемого. Дополнительное линейное слагаемое, входящее в периодическое решение возмущенной системы и принадлежащее к дополнению корневого пространства, имеет вид

y(t,£) = elMtb + e~lwtb, где b Е С4 находится из системы линейных алгебраических уравнений

(

B₀ — £B 1 +Re(S) wA — Im(S) уНе^Х _eRe(h)\

—шА + Im(S)   B₀ — £B 1 + Re(S) Ilm(b))  Ilmhh))'

-

Здесь h = colon(0,r₁e^iei,0,r₂e¹⁰²),

S -(2 х 2) — матрица , элементы которой

вычисляются по формулам

П

S = ^k,

к=1

₇ ⁽¹⁾ _ р ^(Pfc)

^z k   = ^в 1 9 к ,

1 ^Sk~T) o

т ^z k ¹⁾c^t)y /( ¹⁾c^t)dt,

(1) У к

_

= B^,

_ к = 1,п.

Решая систему (5) в случае ш = 1, получим /  (2£ + 1) sin t\

4(£ 2 — 1)  '

(2£ + 1)cost

-

y⁽t, £) =

4(£- — 1) £ sin t

— 277^71

£ cos t к —2(£2 — 1) /

,

y(t,0) =

/ sin cost

к

4 0

.

Решая систему (5) в случае w = 3, получим

y⁽t, £) =

/  (2£ — 1)cos3t\

4(£ 2 — 1)   '

3(2£ — 1)sin2t

4(£ 2 — 1)

£ cos 3t

,

y(t,0) =

-

2(£ 2

-

cos 3t

(-  4

3sin3t

к —

3с sin 3t

2(£ 2

-

/

к 0  /

Периодические решения возмущенной и невозмущенной систем. C использованием математического пакета Maple методом Ляпунова-Шмидта [5] построены следующие периодические решения возмущенной и невозмущенной систем.

Единственное T -периодическое решение системы (2) имеет вид [5]

n ^{P k}

X(t,£) = ^^^^ (^ ki ^ k ⁷⁾ + 41<й⁷⁾) +y(t,c), k=1 ; = 1

где ^k1 определяются из равенств fki = —^(^ki + fe£ + fee2 + - + 9kpkcPk 1),    k = 1,n.

Семейство T -периодических решений системы (3), имеет вид [5]

X(t, 0) = xt) = £ c k [? k“ + ?“] + xt, 0),

k=1

• 1)    Случай to = 1. По формулам (6) и (7) найдем 2тт-периодические решения систем (2) и (3), соответственно,

  X(t,£) =

  
  
  
  

  -

  
  

  к

  
  

  cos t

  
  

  2с sin t ~2£~ cos t

  
  

  _-

  
  
  
  

  ,     ^^(t) =

  
  

  - c 1 sin 3t — 2c₂ sin t + - cos t \

  
  

  2с sint “2Т /

  
  

  к

  
  

  2c, cos 3t — 2c? cos t — -sin t

  ^{1              2}         4

  - c 1 sin 3t + 2c₂ sin t

  2c 1 cos 3t + 2c₂ cos t

  
  

  ■

  
  

  /

  
  

• 2)    Случай to = 3. Учитывая формулы (6) и (7), найдем ^-периодические решения систем

• (2) и (3), соответственно,

  X(t, с) =

  
  

  / sin 3t

  — 2с

  3 cos 3t

  2с sin 3t

  
  

  _-

  
  

  _-

  
  
  
  

  ,     ^^(t) =

  
  

  / — c 1 sin 3t —

  
  

  2e

  3 sin 3t

  к   2с^- /

  
  

  2c 1 cos 3t —

  
  

  к

  
  

  - sin 3t\ 4

  - cos 3t

  
  

  - c 1 sin 3t 2c 1 cos 3t

  
  

  ■

  
  

  /

  
  

Построение графиков компонент периодических решений возмущенной системы.

Учитывая, что обобщенным координатам q 1 и q₂, соответствуют компоненты X 1 (t, г) и x₃(t,£) периодического решения возмущенной системы (2), приведем графики этих компонент при различных £ в случаях 1) ш = 1 и 2) ш = 3.

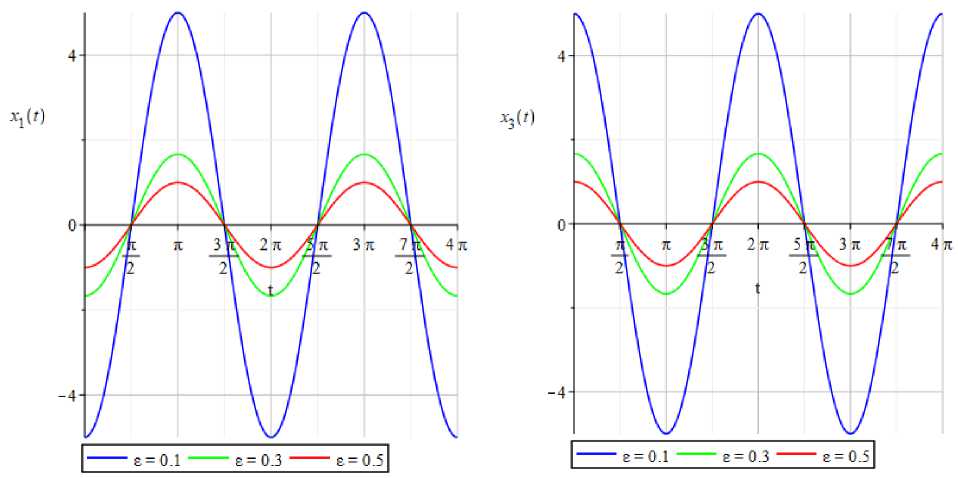
а) X^t^);                                     б) X 3

Рис. 1. Графики компонент а) X 1 (t, г) и б) x₃(t, г) 2я-периодических решений

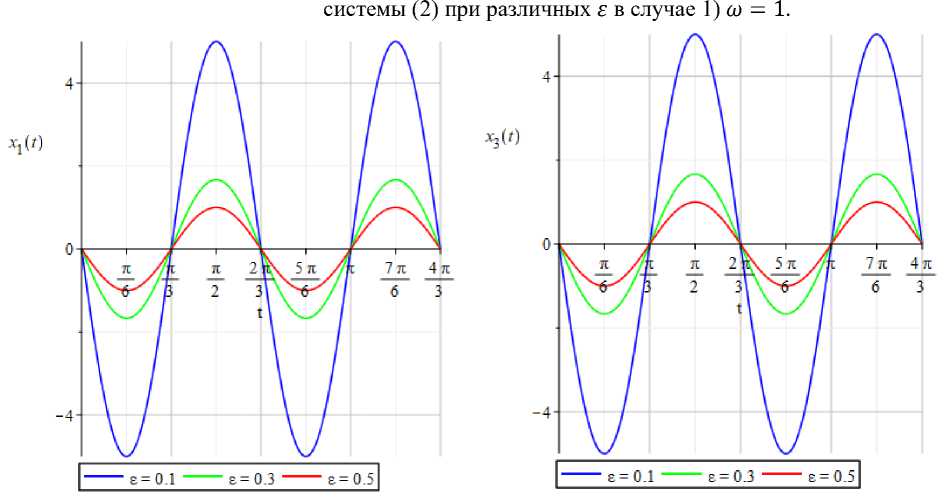
а) X 1 (t, г);

б) X3(t, г);

Рис. 2. Графики компонент а) X1(t, г) и б) x3(t, г) —-периодических решений системы (2) при различных г в случае 2) ш = 3.

Построение графиков проекций фазовых траекторий возмущенной и невозмущенной систем. Приведем графики проекций фазовых траекторий возмущенной и невозмущенной систем (2) и (3).

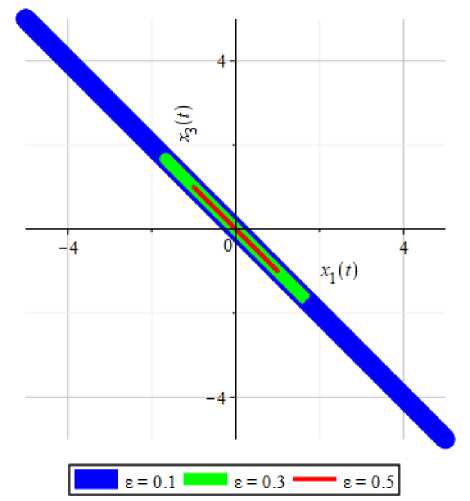
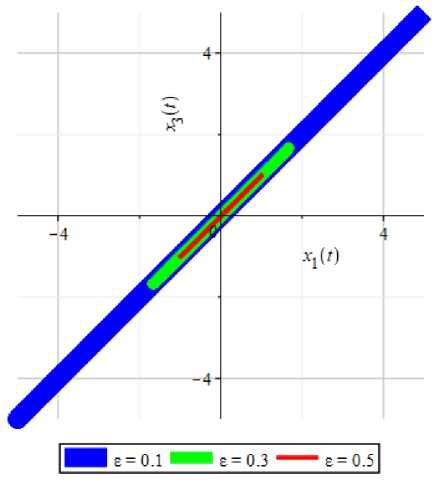
a) to = 1

б) to = 3

Рис. 3. Графики проекций фазовых траекторий на плоскость (Хр х3) возмущенной системы (2) при различных г в случае а) to = 1 и б) to = 3.

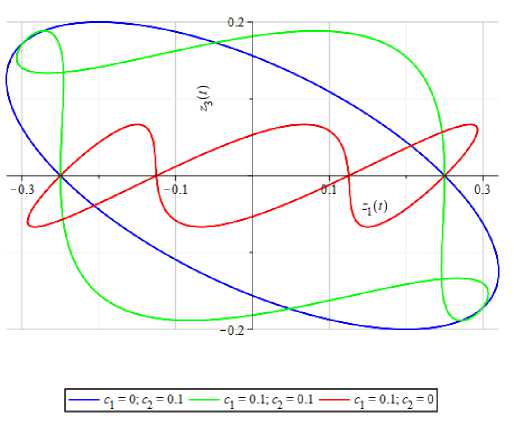
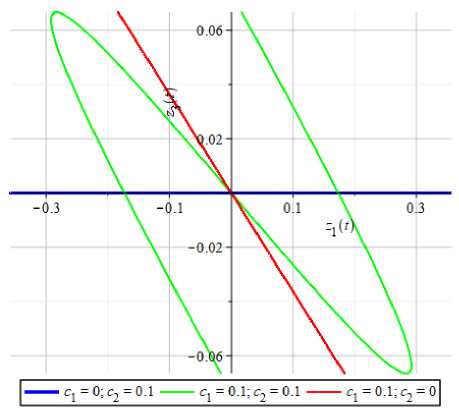
а) to = 1

• б)    to = 3

Рис 4. Графики проекций фазовых траекторий на плоскость (z1,z3) невозмущенной системы (3) при различных г в случае а) to = 1 и б) to = 3.

Заключение. Из формул (4) и (5) следует, что периодические решения x(t,s) возмущенной системы (2) в случаях 1) w = 1 и 2) w = 3 имеют полюс первого порядка в точке £ = 0, и, следовательно, при е ^ 0 не стремятся к соответствующим решениям z(t) невозмущенной системы (3). Наличие полюса первого порядка обуславливается тем, что коэффициенты д₂₂ в случае 1) w = 1 и д₁₂ в случае 2) w = 3 отличны от нуля.