Исследование взаимодействия водорода с границами зерен в α-FE

Благодаря своей низкой стоимости и высоким механическим свойствам, сталь является одним из наиболее важных и широко используемых металлических материалов. Дефекты и примеси играют в ней важную роль, поскольку они могут как улучшать, так и ухудшать эксплуатационные качества стали. Многочисленные исследования показывают, что границы зерен (ГЗ) являются активным элементом дефектной структуры материалов. ГЗ представляет собой плоский дефект атомной структуры. Благодаря природе этого дефекта, связь между отдельными атомами на границе зерна меняется по сравнению со связью в регулярной кристаллической решетке [1]. Из-за формирования в области контакта зерен специфической структуры отличной от структуры совершенного кристалла, свойства границ могут быть иными, чем у объема. Структура ГЗ может быть определена с помощью экспериментальных методов, таких как метод просвечивающей электронной микроскопии высокого разрешения и рентгенодифракционный метод. Тем не менее, достаточно трудно получить точные данные термодинамических величин на границе раздела. Поэтому неэмпирические квантово-механические методы, основанные на теории функционала плотности, являются наиболее подходящим инструментом для получения достоверной количественной информации о структуре ГЗ и энергии на электронном уровне.

Известно, что водород оказывает значительное влияние на физические и механические свойства железа и сплавов на его основе [2, 3]. Это явление называется водородное охрупчивание (ВО) [4], и на сегодняшний день до сих пор не полностью изучено. Самые популярные теории, которые пы- таются объяснить ВО являются теория индуцированной водородом атомной декогезии (HEDE – hydrogen-enhanced decohesion [5] и механизм водородного усиления локальной пластичности (HELP – hydrogen-enhanced localized plasticity) [6]. В этой статье акцент делается на рассмотрении первого механизма. Основная идея модели HEDE предполагает, что растворенный водород уменьшает силу, необходимую для разделения кристаллов вдоль кристаллографических поверхностей, таких как границы зерен или межфазные границы, и, соответственно, уменьшает энергию для образования поверхности раскола и, таким образом, способствует образованию трещин.

Теоретические исследования взаимодействия водорода с границами зерен ОЦК-железа все еще ограничены определенными типами границ. Граница Σ3(111) достаточно хорошо изучена. В рамках теории функционала плотности было проведено моделирование взаимодействия водорода с Σ3(111) в железе [7–10]. Эти результаты показали, что водород является сильным охрупчивате-лем для данной границы. Есть несколько работ посвященных исследованию Σ5(310) [11–13], которые свидетельствуют о захвате атома водорода междоузлиями. Моделирование взаимодействия водорода с границей Σ5(210) выполнено лишь в одной работе [14] и недостаточно подробно. В связи со всем вышесказанным, целью данной работы является изучение взаимодействия водорода с границами зерен Σ5, а также с целью тестирования расчетной схемы с одной из наиболее изученных ГЗ – Σ3(111). В этой работе, структурные, электронные и магнитные свойства этих ГЗ были исследованы с помощью программного пакета WIEN2k.

Методика

Б ыл и в ыбраны три гра ни ц ы з е ре н на кл о на Σ3(111), Σ5(210) и Σ5(310). Г ра ни ц а Σ3(111) явля етс я на и бол е е ча с то изуча ем ой и м ож е т ра с с мат р и в а ть с я в ка че с т в е м оде льной с исте м ы [7 –10]. Граница Σ5(310) и м ее т н из к ую эне рг ию форм ирования в ОЦК- ж е л е з е [12]. Не с м отря на то, что Σ5(210) ме не е изуче на , дан на я гра н ица ин те ре с на из-з а в з аим ного с дв ига од н ого з е рна относ ител ьно другого, который создает а с им м е трию в сис те м е . П оэтом у е е м ож но ис по л ь з ов а ть как м оде л ь д л я ас им м е тричны х гра н иц н ак лона в ж е л е з е .

Построение суперячеек границ зерен наклона осуществлялось с помощью модели решетки совпадающих узлов (РСУ) [1]. РСУ обычно характеризуется величиной Σ, которая равна обратной доле совпадающих узлов. В случае границ зерен Σ5(210) и Σ5(310) соприкасающиеся решетки ОЦК-железа поворачивались друг относительно друга вокруг общей оси [001] примерно на 53,1 и 36,9°, соответственно, а плоскости (210) и (310) определялись в качестве плоскостей границ зерен. Аналогичным образом, была построена граница зерна Σ3(111). В этом случае осуществлялся поворот вокруг общей оси [110] примерно на угол 70,53°, а плоскость (111) использовалась как плоскость границы зерна. Модели межзеренных границ Σ5(210), Σ5(310) и Σ3(111) представляют собой элементарные ячейки из 40, 40 и 48 атомов, соответственно (рис. 1). Дальнейшее увеличение размера суперячейки приводит к незначительным изменениям ее энергии формирования (порядка 0,01 Дж/м2). Следовательно, размер этих систем является достаточным для моделирования взаимодействия водорода с границами зерен.

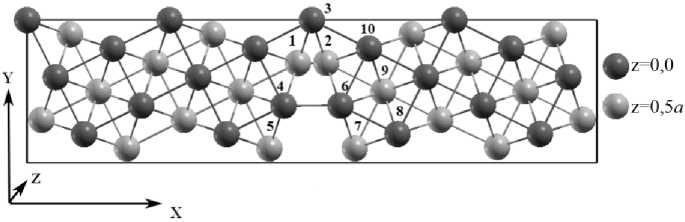
а)

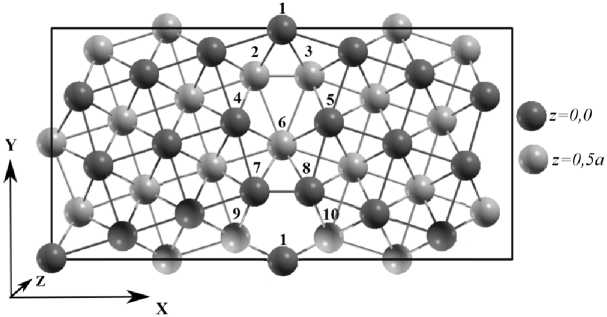
б)

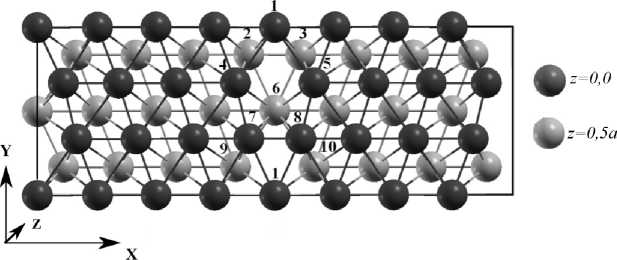
в)

Рис. 1. Схематическое изображения границы зерна α -железа: а) Σ5(210); б) Σ5(310); в) Σ3(111)

Две половины ячейки из-за периодичности, по существу, представляют собой два «зерна» и две границы. Суперячейка свободной поверхности (СП) моделируется путем замены одной из половинок ячейки (зерна) вакуумом в 10–12 Å. Таким образом, СП представляет собой 20 (для Σ5(210) и Σ5(310)) или 24 (для Σ3(111)) атома отделенных от соседней ячейки вакуумом в 10–12 Å в направлении оси x .

Все вычисления проводились в рамках теории функционала плотности полнопотенциальным методом линеаризованных присоединенных плоских волн (FP LAPW) [15] с учетом обобщенного градиентного приближения (GGA’96) [16] в программном пакете WIEN2k [17]. При интегрировании в обратном пространстве и вычислении электронной плотности использовалась схема Монхор-ста– Пака [18] с сеткой 8 × 4 × 1 k -точек зоны Бриллюэна для Σ5(210) и Σ5(310), и 6 × 4 × 2 k -точек для Σ3(111). Дальнейшее увеличение k -точек приводит к несущественным изменениям полной энергии систем, не более чем на 0,01 эВ. Радиус МТ-сферы R mt был равен 2,0 а.е. и 0,7 а.е. для железа и водорода, соответственно, K max = 5,0 а.е.^-1, E cut =–7 Рб (340 эВ) [19]. Размерности суперячеек ГЗ ( a , b , c ) для Σ5(210), Σ5(310) и Σ3(111) были (4 5 a , 5 a , a ), (2 10 a , 10 a , a ) и (4 3 a , 6 a , 2 a ) соответственно, а плоскости ГЗ были перпендикулярны оси x . Здесь a является постоянной решетки ОЦК-железа. Для Σ3(111) был найден равновесный параметр решетки равный 2,84 Å, а для Σ5(210) и Σ5(310) – 2,847 Å, эти значения находятся в хорошем согласии с экспериментальными данными 2,86 Å [20]. Таким образом, суперячейки имели следующую площадь границ зерен 18,12, 25,63 и 27,94 Ų/ячейку для Σ5(210), Σ5(310) и Σ3(111), соответственно.

Релаксация структуры проводилась следующим образом. Для каждого типа ГЗ, построенного как описано выше, была оптимизирована длина суперячейки как вдоль, так и по направлению нормали к границе, для того чтобы удалить в су-перячейке возникшие при образовании межзеренной границы напряжения. После этого проводилась основная релаксация положений отдельных атомов в суперячейке в соответствии с силами Хеллмана – Фейнмана до тех пор, пока результирующая сила на каждом атоме не превышала 0,01 эВ/Å. Эти параметры обеспечивают погрешность результатов расчетов не более 0,01 эВ.

При исследовании межмолекулярного взаимодействия и механических свойств ГЗ энергию её формирования определяют двумя способами:

• 1)    согласно термодинамической теории Райса и Вана [21]:

Y f = E gb ^{- 2} E fs [эВ/атом], (1) где E gb – полная энергия ГЗ; Е fs – полная энергия СП;

• 2)    в рамках подхода ab initio Y gb = E gb - E bulk , [Дж/м²],

  
  

где E gb – полная энергия границы зерна; E bulk – полная энергия объемного кристалла, который имеет тот же объем и форму суперячейки, как у границы зерна; S – площадь поперечного сечения суперячейки.

Следует отметить, что отрицательное значение энергии формирования y _f, определяемой формулой (1), соответствует уменьшению свободной энергии системы за счет ликвидации двух поверхностей, т. е. этот процесс является энергетически выгодным.

Влияние водорода на свойства границы зерна можно описать с помощью трёх количественных характеристик:

• 1)    энергия растворения:

A E = E gb - E _g b - 2 E H , (3)

где Egb – полная энергия суперячейки без примеси, EgHb – полная энергия такой же суперячейки с водородом, E – энергия молекулы H2 в вакууме.

H2

Отрицательный знак энергии растворения говорит о том, что водород легко растворяется на границе зерна;

• 2)    энергия когезии, величина которой указывает либо на усиление (отрицательное значение), либо на ослабление межмолекулярной связи на ГЗ в присутствии примеси:

A E в = E gH - E gb + E f _s - E H , (4) где E _fs – полная энергия суперячейки свободной поверхности Fe, а E _f ^H _s – полная энергия супер-ячейки свободной поверхности с одним атомом H;

• 3)    энергия связи водорода с границей зерна:

E gm = E gbb - E gb + E bulk - E Hulk , (5) где E _bulk – полная энергия соизмеримой объемной суперячейки Fe, а E _b ^H _ulk – полная энергия этой су-перячейки с одним атомом водорода в междоузлие.

Результаты

Во время моделирования возникла проблема из-за достаточно близкого расположения атомов 1 и 2 (рис. 1, а) для угла наклона 53,1°. Как отмечено выше, в данном пакете реализован метод LAPW, в котором пространство ячейки разбивается на не-перекрывающиеся атомные сферы и междоузель-ную область. Это разбиение соответствует разделению остовных и валентных состояний электронов. При близком расположении атомов во избежание перекрывания остовных электронов приходится выбирать слишком маленький параметр Rmt, что ведет к искажению кристаллического потен- циала и программой не допускается. Поэтому было необходимо определить оптимальный жесткий сдвиг одного зерна относительно другого, что позволило бы увеличить параметр Rmt до разумного значения. Сдвиг осуществлялся по направлениям осей x (для увеличения Rmt) и y (для уменьшения пустого пространства на границе зерна, образовавшегося в результате разориентировки зерен). Вдоль направления оси x был сделан жесткий сдвиг 0,2–0,5 Å с шагом 0,1 Å, а вдоль y – 0,2–0,8 Å с шагом 0,2 Å. Был построен график зависимости энергии формирования границы зерна (по формуле (1)) от жесткого сдвига (рис. 2). Было получено, что минимальной энергии формирования границы зерна отвечает конфигурация со сдвигами 0,4 Å по оси x и 0,6 Å по оси y.

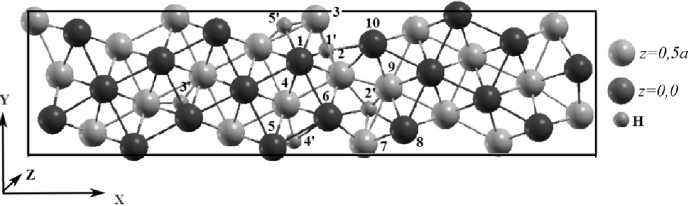
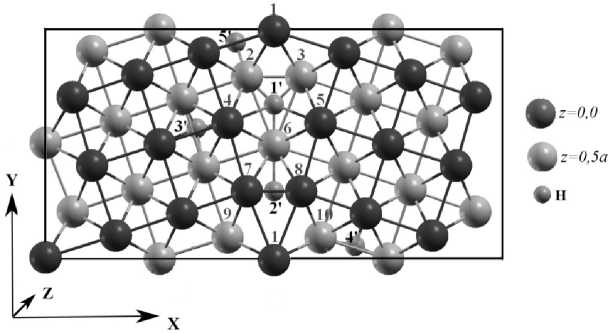
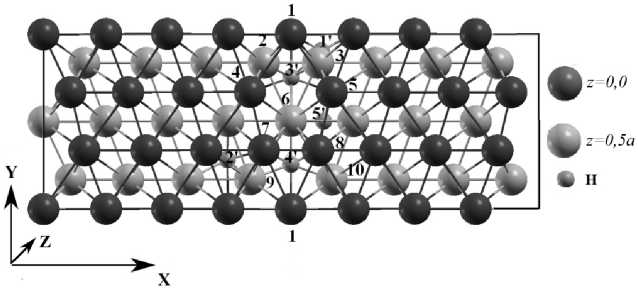
При ис с ле дов ан ии гр а ни ц зере н Σ 5(310) и Σ 3 (11 1) н ео б ход и м о сть же с тк о г о с д ви га о дн ог о зерна относительно другого о тсу тс тво в ала. Дл я к ажд ой и з г р а ни ц б ы л а в ыпо лне на о пти ми за ци я геоме т р и и пр и по с т о я н ном об ъеме. И таки м об ра з ом, б ы л и н ай д ен ы о пт и ма ль н ые ко н ф игу р ации систем. В к аждо й гран и це зер н а б ы л и и с сле д ов а ны 5 по з и ц ий а тома вод оро д а ( рис . 3) . В таблице представлен ы э не р ге тиче с к ие хара к т е р ис тики взаи м о д е йс т в и я во д ор ода с г ран ицами зерен.

Результаты показывают, что абсолютные значения энергии образования границы зерна (1) Σ3(111) по порядку величины согласуется с другими данными [22]. Энергия формирования границ зерен γgb (2) для Σ5(210), Σ5(310) и Σ3(111) равны 1,83, 1,44 и 1,46 Дж/м2, что хорошо согласуется с ранее полученными результатами в рамках теории функционала плотности [11, 22, 23]. Кроме того энергия для Σ5(310) ниже, чем для Σ3(111), что также подтверждается как в методе теории функционала плотности, так и в методе молекулярной статистике [23]. Экспериментальные значения, представленные в [24, 25], составляют 0,77 и 0,985 Дж/м2. Эти значения приблизительно в 1,5–2,0 раза меньше чем наш результат, вероятно, это связано с тем, что они являются средними значениями для границ зерен, встречающихся в железе, и не относятся к определенным разориентировкам границ.

Отрицательный знак энергии растворения (3) говорит о том, что водород легко растворяется на границе зерна. Аналогичные результаты были получены и в других теоретических работах [10, 11, 13]. А положительное значение энергии когезии (4) указывает на то, что водород ослабляет межмолекулярную связь на границе зерна [8]. Во всех случаях, три границы зерна, Σ5(310), Σ5(210) и Σ3(111), действуют как ловушки для водорода с энергией захвата 0,43; 0,81 и 0,39 эВ, соответственно. Эти значения находятся в хорошем согласии, как с другими теоретическими результатами [9, 11, 14] так и с экспериментальными значениями [26]. Вероятно, пустоты на границе создают похожую ситуацию для водорода, как и вакансии внутри объема, для которых энергия захвата составляет 0,60 эВ [27]. Отметим, что полученное нами значение энергии связи для случая ГЗ Σ 5(210) существенно ближе к данным эксперимента, чем заниженная величина, приведенная в работе [14]. Возможно, это связано с недостаточно хорошим выбором в [14] жесткого сдвига одного зерна относительно другого и использованием кода ASED-MO, точность которого не слишком высока. На энергию захвата атома водорода влияет не только объем (с увеличением объема увеличивается энергия), но также и асимметрия структуры.

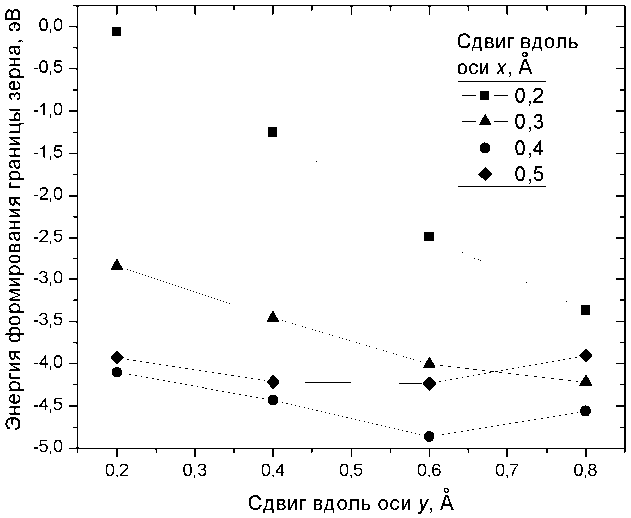
Рис. 2. График зависимости энергии формирования границы зерна от жесткого сдвига

а)

б)

в)

Рис. 3. Схематическое изображение положений атома водорода на границе зерна: a) Σ5(210) – оптимальное положение 2 ′ ; б) Σ5(310) – оптимальное положение 2 ′ ;

в) Σ3(111) – оптимальное положение 4 ′

Энергетические характеристики границ зерен

	Д а нн ая ра бот а			Другие результаты			Эксп.
	Σ5(310)	Σ 5(210)	Σ3(111)	Σ5(310)	Σ5(210)	Σ3(111)
γ f (1), эВ/ат	–5,77	– 5, 24	–4,19	–	–	–3,27 [22]	–
γ gb (2), Дж/м2	1,44	1 , 83	1,46	1,48 [23], 1,53 [11]	2 [22]	1,52 [23]	0,77 [24], 0,985 [25]
Δ E (3), эВ	–0,1	– 0, 48	–0,1	–0,13 [11], –0,14 [13]	–	–0,19 [10]	–
Δ E B (4), эВ	0,68	0 , 07	0,41	–	–	0,31 [8]	–
E gbbinH (5), эВ	0,43	0 , 81	0,39	0,4 [11]	0,13 [14]	0,49 [9]	0,51 [26]

Заключение

Были выполнены неэмпирические расчеты энергии формирования границ зерен и атомных конфигураций Σ5(310), Σ5(210) и Σ3(111) с и без водорода. Результаты для энергии формирования границ зерен находятся в согласии с существующими данными. Границы зерен Σ5(310), Σ5(210) и Σ3(111) могут выступать в качестве ловушек для водорода с энергией захвата 0,43; 0,81 и 0,39 эВ соответственно. Энергия связи для Σ5(310) и Σ3(111) меньше энергии захвата вакансией, в то время как в случае с Σ5(210) она становится выше. Возможно, что такая особенность ГЗ Σ5(210) связана с асимметричной конфигурацией атомов.

Исследование поддержано грантом Российского научного фонда №16-19-10252.