Исследование взаимосвязи между параметрами строения ткани и ее защитной способностью при прорезании

DOI:

При проектировании оптимальных структур защитных тканей на основе высокопрочных и высокомодульных нитей, предназначенных, в первую очередь, для изготовления мягкой бронезащиты или противопро-кольной и противопорезной экипировки и спецодежды, необходимо иметь четкие представления о механизмах разрушения тканей с заданными параметрами строения при воздействии поражающих элементов определенной формы и с определенной скоростью/энергией.

Основной проблемой создания эффективных средств индивидуальной защиты от различных поражающих воздействий является проблема неполной реализации механических свойств высокопрочных и высокомодульных нитей в составе изделия.

Причинами неполной реализации свойств нитей в составе изделий или в отдельных слоях текстильных полотен, являются, во-первых, снижение механических свойств высокопрочных и высокомодульных нитей по переходам ткацкого производства, во-вторых, особенности строения ткани: переплетение нитей основы и утка, степень изгиба нитей в элементе ткани, длина основных и уточных перекрытий, степень закрепления и связность ткани.

Задача проектирования оптимальных структур тканей, защищающих от ударных, колющих и режущих воздействий осложняется многофакторностью механизма взаимодействия поражающих элементов (скорость воздействия, тип индентора) с тканью (Elgohary, 2024). Отсутствие научно обоснованного представления о механизме взаимодействия поражающего элемента и текстильных материалов различных структур, приводит к тому, что задача повышения эффективности защиты решается в каждом конкретном случае методом проб и ошибок.

При анализе литературных источников, посвященных вопросам оценки эффективности защитных текстильных материалов, было установлено, что существует два противоречащих друг другу подхода к выбору защитных тканей.

По мнению некоторых исследователей (Elgohary, 2024; Sadegh & Cavallaro, 2012;

Исследователями (Григорян, Кобылкин, Маринин и Чистяков, 2008; Харченко и Ермоленко, 2013; Харченко, 2014; Харченко, 2005) считается, что нити в ткани должны иметь возможность вытягиваться и раздвигаться, что должно привести к большим затратам энергии на преодоление сил трения, это позволяет более эффективно и раньше тормозить поражающий элемент.

Перечислим основные составляющие механизма взаимодействия поражающего элемента с текстильными защитными структурами, известные из многочисленных экспериментальных исследований Е.Ф. Харченко (Харченко и Ермоленко, 2013; Харченко, 2014; Харченко, 2005). Во-первых, происходит частичное или полное разрушение волокон в результате поперечного сжатия, во-вторых, разрушение волокон растягивающими нагрузками, в-третьих, происходит вытягивание нитей из структуры ткани, в-четвертых, имеет место раздвижка систем нитей, сопровождающаяся трением проникающего поражающего элемента о края образующегося отверстия. Таким образом, сделан вывод о том, что максимальная доля энергии поражающего элемента (40–50 %) поглощается именно за счет фрикционной составляющей при вытягивании и раздвижке нитей, а не за счет их растяжения, приводящего к непосредственному разрыву. Поэтому можно сделать вывод о том, что при проектировании защитных тканей важно получить оптимальное сочетание между усилием вытягивания нитей, раздвижкой систем нитей и прочностью отдельных нитей.

Также стоит отметить, что современные тенденции проектирования и применения защитных тканей на основе арамидных нитей направлены на широкое внедрение так называемых 3D тканей (многослойные ткани с различным способом соединения слоев). По мнению целого ряда авторитетных исследователей (Kumar et al., 2016; Grechukhin, Seliverstov & Rudovskiy, 2017; Рудовский и Гречухин, 2025; Abtew et al., 2020; Abtew et al., 2018) использование 3D тканей позволяет повысить защитные свойства бронепакетов. Однако остается не исследованным вопрос о реализации свойств нитей в данных структурах, их повреждаемости в процессе ткачества и способности вытягиваться и раздвигаться под действием ударных нагрузок.

Таким образом, цель данной работы заключалась в изучении особенностей деформирования защитных тканей различных структур при низкоскоростном внедрении индентора в виде ножа и установлении взаимосвязи между параметрами строения ткани и особенностями ее деформирования.

Аналитическая часть

В качестве объекта исследования выбрана арамидная ткань с поверхностной плотностью порядка 160 г/м2, изготовленная на рапирном станке из комплексных нитей Руслан 29,4 текс с использованием различных вариантов переплетений.

Опишем геометрию структурного элемента изготовленных вариантов ткани. Для этого рассмотрим ткань в свободном состоянии, т. е. при отсутствии внешних нагрузок. Нить, изогнутая при тканеформировании, стремится восстановить свою прямолинейную форму, что приводит к возникновению усилий, действующих в области контакта перекрещивающихся нитей. Результирующей распределенных сил выступает сила, являющаяся следствием взаимодействия двух соприкасающихся нитей.

Определим длину осевой линии упругой нити l на участке 01 (рисунок 1), а также угол φ между осью нити

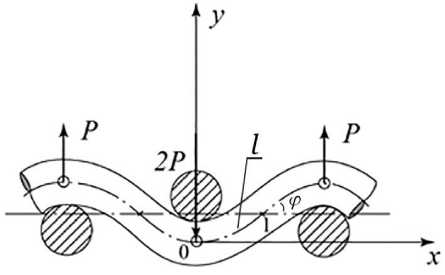
Рисунок 1 – Изгиб консольной упругой нити в структурном элементе ткани на участке 01 Figure 1 – Bending of the cantilever elastic thread in the structural element of the fabric on Site 01

и нейтральной линией в точке 1, эллиптические параметры k и α ₀ (модуль эллиптического интеграла и его амплитуда, соответственно), уработки нитей основы и утка, и величины силы давления основы на уток и утка на основу P .

Приведем систему уравнений для определения четырех неизвестных l , k , α ₀ , P согласно методике, изложенной в [(Попов, 1986; Щербаков и Скуланова, 2008; Щербаков, 2011):

F(k) — F(a₀) = co , к sin a₀ = ^2 ,

^=1—;[Е(к) —Ffa.)], ^- = 2ksinao .(1)

l01         w                       ^01

Принятые обозначения:

F(ao) = Cvi-Xn^ E(a0) = S^^-^srfada, “ = № F(v = h=m•

Поясним некоторые принятые обозначения. Индексом 0 будем обозначать величину в недеформирован-ном состоянии, индекс 1 относится к нити основы, индекс 2 к нити утка. Для определения длины участка 01 (координаты x₁ и x₂ ) необходимо воспользоваться следующими выражениями:

xt = Ь^ и хг=^ ,(3)

14  24

где l0 = — _ ly = _y — геометрическая плотность по "o основе и утку, мм; Po и Py – фактическая плотность по основе и утку, нить/мм; Ro и Ry – раппорт по основе и утку.

Для определения координат y₁ и y₂ разделим высоты волн изгиба основы h_o и утка h_y , определенные из микросрезов ткани, пополам:

ho        hy

У1 = т ^и У2 = 7 ,

где h_o и h_y – высоты волн изгиба основы и утка в ткани, мм.

Теперь, зная координаты x и y для случая основных и уточных нитей, и зная, жесткость арамидной нити Руслан 29,4 текс при изгибе H = 3,1 cН·мм² (жесткость при изгибе определена в соответствие с методикой (Егоров, 2010)) легко построить решение системы (1) с учетом (2) в среде MathCAD.

Определив длину осевой линии нити основы и утка можно вычислить их уработку:

a₀ = ^-^ • 100 и a_v = ^ 02 -^ 2 • 100 .   (5)

^ 01                 ⁷       ^ 02

Зная эллиптические модули, определим угол наклона касательной в концевой точке для недеформирован-ного состояния:

p₀₁ = 2arcsin ^ i — “ и p₀₂ = 2arcsin k₂ — ^ . (6)

В таблице 1 представлены результаты расчета геометрических параметров элементарной ячейки для арамидных тканей различных переплетений.

Из таблицы 1 следует, что для рассмотренной ткани полотняного переплетения наблюдаются колоссальные значения силы взаимодействия нитей. В высокоплотной ткани полотняного переплетения, где нити основы имеют изгиб гораздо больше, чем нити утка (порядок фазы строения, ПФС = 8) - рисунок 2, давление утка на основу составляет P 1 = 102,5 сН, а давление основы на уток Р₂ = 17,сН, т. е. в 6 раз меньше. Это с одной стороны обеспечивает структуре ткани монолитность, но с другой стороны приводит ткань в состояние с ярко выраженной анизотропией свойств.

Для ткани переплетения саржа 3/3, напротив, наблюдается случай равенства нагрузок, действующих со стороны основы на уток и со стороны утка на основу, равенство уработок нитей ПФС = 5 (рисунок 3), что свидетельствует об однородности свойств по основе и утку.

Для более полного понимания факта анизотропии свойств защитных тканей необходимо обратиться к теории двухосного растяжения и расчету прочности ткани с учетом параметров ее строения и свойств нитей основы и утка. Теория двухосного растяжения ткани и методика расчета прочности ткани приводятся в соответствие с положениями, разработанными проф. Kawabata S. (Kawabata, Niwa, and Kawai, 1973) и проф. В.П. Щербаковым (Щербаков, 2011; Щербаков и Скуланова, 2008).

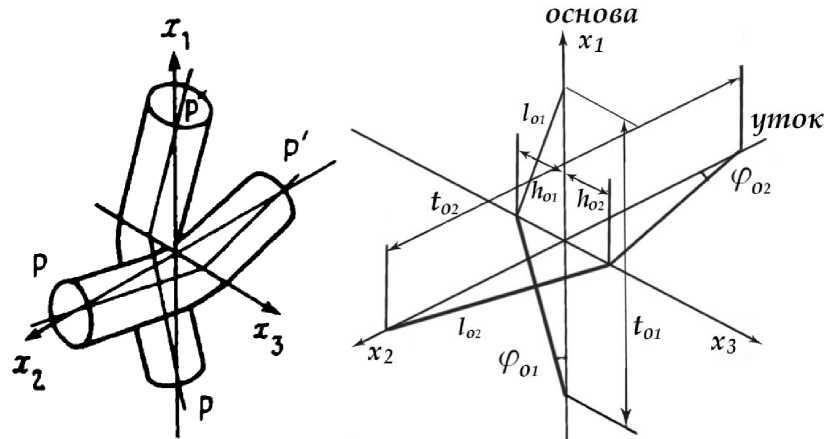
Рассмотрим ткань под действием растягивающих нагрузок, направленных вдоль нитей основы (ось х 1 ) и утка (ось х₂ ), полагая нерастяжимость оси нити. Тогда, натяжение нити, возникающее при деформировании ткани, распрямляет изогнутую нить. Реальная структура ткани заменяется моделью, в которой оси нитей основы и утка представлены прямыми линиями с точкой перегиба в месте пересечения нитей (рисунок 4).

Рассмотрим двухосное растяжение вдоль осей х 1 и х₂ . Обозначим шаг или длину структурного элемента вдоль основы (ось х 1 ) через t₀₁ , а вдоль оси х₂ через t₀₂ . Длина структурного элемента связана с плотностью нитей в ткани и раппортом ткани:

^ 01 =^ ^{И f} 02 = ^ . ⁽⁷⁾

Г у г₀

Таблица 1 – Значения геометрических параметров элементарной ячейки арамидных тканей различных структур

Table 1 – Values of geometric parameters of the unit cell of aramid fabrics of various structures

Переплетение ткани	Эллиптические параметры				Длина осевой линии, мм		Сила взаимодействия, сН		Углы наклона нити к нейтральной линии, град.		Уработка нитей, %
	k 1	k 2	α01	α02	l01	l02	P 1	P 2	φ01	φ02	a o	a y
Полотняное	0,90	0,75	0,90	1,24	0,22	0,20	102,5	17,0	39,5	6,6	12,5	0,4
Саржа 1/5	0,82	0,81	1,04	1,06	0,49	0,55	9,2	6,2	20,7	18,0	3,5	2,6
Саржа 3/3	0,77	0,77	1,16	1,16	0,54	0,61	3,8	3,0	10,9	10,7	1,0	0,9
Репс уточный 3/3	0,73	0,81	1,30	1,07	0,20	0,57	11,3	5,7	4,5	17,7	0,2	2,5
Рогожка 3/3	0,76	0,78	1,19	1,14	0,63	0,56	2,4	4,0	9,3	12,5	0,7	1,3
Атлас шестиремизный	0,79	0,76	1,10	1,20	0,59	0,60	4,4	2,4	14,7	8,5	1,8	0,6

a вдоль основы (along warp thread)

б (b)

вдоль утка (along weft thread)

Рисунок 2 – Микросрезы ткани полотняного переплетения

Figure 2 – Cross section of plain weave fabric

a вдоль основы (along warp thread)

б (b)

вдоль утка (along weft thread)

Рисунок 3 – Микросрезы ткани переплетения саржа 3/3

Figure 3 – Cross section of 3/3 twill fabric

На границах ткани действует растягивающая сила f_i ( i = 1, 2). Если на длину ткани приходится n_i нитей, то на конце одной нити по оси x_i действует сила F_i = f_i / n_i (рисунок 5). При растяжении ткани по обеим осям в нитях возникает натяжение T_fi , связанное с силой, действующей на ткань:

F_i = T_ficos

i

, (8)

где φ_i – угол между осью нити и нейтральной линией структуры в деформированном состоянии.

При моделировании растяжения ткани полагается, что расстояния между нитью основы и утка на линии их контакта сохраняются постоянными при условии неизменных поперечных размеров нитей:

ℎ₁ + ℎ₂ = ℎ₀₁ + ℎ₀₂ .            (9)

В деформированном состоянии также должно выполняться следующее уравнение равновесия для сжимающих сил основы и утка:

^F c i = ^F c 2 .                  (10)

б (b)

a

Рисунок 4 – Модель структурного элемента ткани (а) и расчетная схема (б)

Figure 4 – The model of the structural element (a) of the fabric and the design scheme (b)

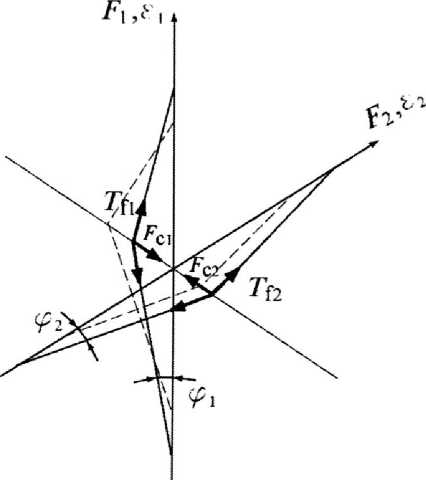
Рисунок 4 – Модель силового взаимодействия основы и утка в элементе ткани

Figure 5 – Model of force interaction of warp and weft in a fabric element

Натяжение арамидной нити определяется ее деформацией в соответствие со степенной зависимостью вида σ(ε) = E · ε^b , параметры E и b легко определить на основании кривых деформирования нити, тогда натяжение нити в Ньютонах равно:

^Tfi = ^Efi -^ fi

,

Y i

где T_i – линейная плотность нити основы или утка, текс; γ_i – плотность нити, г/см³; E_fi и b_i – параметры степенной функции, описывающей кривую растяжения нити, E_fi в ГПа, b_i – безразмерный параметр; ε_fi – предельная деформация нити для случая расчетов прочности ткани.

Деформация ткани ε_i связана с деформацией нити ε_fi зависимостью:

^E fi ~Г ^l0i

—

1 =

' ^ +(1 + E i ) ^L0i

^ oi

—

1 .     (12)

Здесь длина осевой линии нити в недеформирован-ном состоянии l_0i уже определена ранее при решении системы уравнений (1). Длина нити l_0i подвергается

растяжению/распрямлению при нагружении ткани. Далее при начальной длине нити l_0i и шаге структурного элемента t_0i определяется расстояние между нейтральной линией структуры PP’ и осью нити вдоль х₃ в точке перегиба:

^hoi —

sin(l oi ) • l oi 2

Нить утка находится в равновесии под действием сил натяжения T_f2 и реакции N нити основы, направленной по оси х₃ в точке контакта нитей основы и утка. На нить основы действует реакция нити утка N’ , равная по модулю и направленная противоположно силе N . Обе реакции уравновешиваются силами давления нитей друг на друга, которые сжимают нити и вызывают смещение обеих систем нитей по оси х₃ (рисунок 5). В деформированном состоянии имеем h₂ = h₀₁ + h₀₂ – h₁ . Сжимающая сила связана с натяжением нити соотношением F_сi = 2T_fisin(φ_i) , где:

*(„) =        ^        -       ^2>l/t“      . (14)

Jv + p^’     ■. i   .

Из уравнения равновесия (10) и соотношения (12) получим выражение для определения неизвестных:

Сила, растягивающая ткань:

F t = T_fi cosQpd . (17)

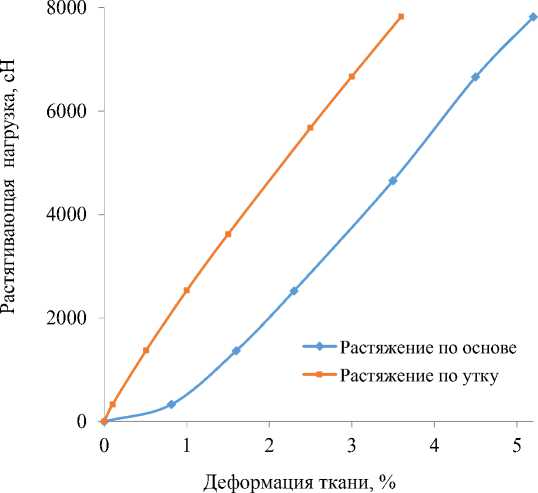
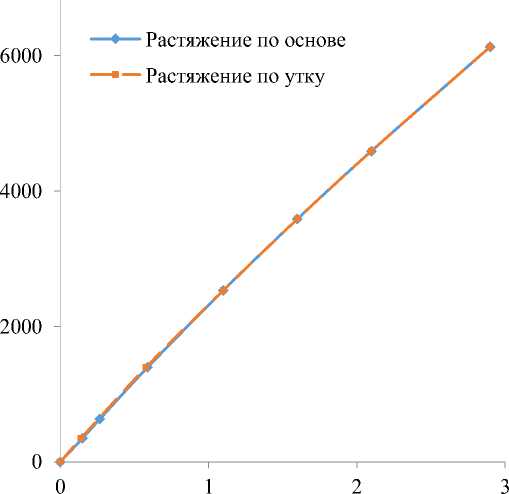
Теперь смоделируем кривые деформирования тканей (из расчета на одну нить). На рисунке 6 представлены расчетные кривые растяжения для основы и утка в ткани полотняного переплетения (неравнодеформа-тивное поведение ткани), а на рисунке 7 представлены расчетные кривые растяжения для основы и утка в ткани саржевого переплетения (равнодеформативное поведение ткани).

При растяжении по основе в ткани полотняного переплетения, порядок фазы строения которой равен 8, на начальном участке кривой наблюдается распрямление сильно изогнутой основы, и только после распрямления изогнутой основы начинается ее непосредственное деформирование. Прямолинейная нить утка в ткани полотняного переплетения начинает деформироваться сразу. В ткани саржевого переплетения характер деформирования основы и утка совпадает, значит, эта структура удовлетворяет условию равнодеформативно-сти (Бова и др., 1999).

Таким образом, предложенное описание растяжения и предельного состояния тканей различных переплетений методами структурной механики позволяет объяснить механизм явлений при деформировании и

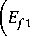
£f1 yJ

⁴^ 1Ао1

'^f + d + E i )² ' ^t01 ⁷

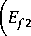
^2 Y 2 )

4(Л о1 + h o2 - h i )/t o2

2⁽^ oi + h o2 - ^t 02

^} + (1 + £ 2 ) 2

Если цель расчета, например, определение прочности ткани в направлении основы, то необходимо задать предельную деформацию нити основы ε_f1 , характеристики нитей ( E_fi , b_i , T_i , γ_i ), структурные параметры в недеформированном состоянии ( h₀₁ , h₀₂ , t₀₁ , t₀₂ ) и положить, что деформация ткани по утку отсутствует ε₂ = 0. После этого необходимо решить (15) относительно ε₁ , h₁ и ε_f2 .

Далее для расчета прочности ткани вычисляем по формуле (11) натяжение нити основы с учетом:

J   ^2hi

i = arctg I              I .

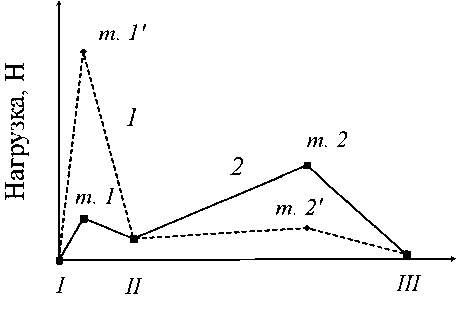
L (1 + Ei)M

нагружении ткани, что имеет принципиальное значение при проектировании защитных тканей с заданными свойствами.

Экспериментальные исследования и обсуждение результатов

Определим основные стадии разрушения тканей при низкоскоростном внедрении индентора в виде двухстороннего ножа и установим влияние степени фиксации (усилия вытягивания) нитей и их способности раздвигаться на устойчивость при прорезании.

Способность ткани сопротивляться внедрению индентора на медленной скорости является, так же, как и способность нитей вытягиваться из ткани, косвенным показателем, по которому можно судить о ее эффек-

Рисунок 6 – Кривые деформирования ткани полотняного переплетения Figure 6 – Deformation curves of plain weave fabric

Деформация ткани, %

Рисунок 7 – Кривые деформирования ткани саржевого переплетения с равной степенью изгиба основы и утка Figure 7 – Deformation curves of twill weave fabric with equal degree of warp and weft bending

тивности в реальных условиях эксплуатации. Однако, преимущество испытаний, проводимых при медленной скорости внедрения, заключается в том, что становится возможным подробно изучить все стадии разрушения, которое сопровождается одновременно разрывом нитей, их раздвижкой и вытягиванием из ткани.

Предложено характеризовать способность ткани сопротивляться внедрению индентора, во-первых, пиковой нагрузкой, при которой структура ткани перестает сопротивляться проникновению, во-вторых, работой деформирования ткани от момента контакта с ней индентора до момента его полного проникновения и беспрепятственного движения, приведенной к массе пробы.

В качестве индентора был выбран двухсторонний нож (тип S1 по стандарту NIJ 0115.00). Испытания по прорезанию предложено проводить на приборе Instron серии 4411 при скорости движения ножа 500 мм/мин. По результатам испытаний строятся диаграммы деформирования ткани.

Испытания проводились таким образом, чтобы лезвие ножа было ориентировано под углом 90 град. к ткани вдоль нитей основы или утка. Это позволяет выявить неоднородность свойств ткани вдоль систем нитей и проверить выполняется ли условие ее равнодеформа-тивности.

В таблице 2 представлены результаты испытаний по прорезанию одного слоя ткани двухсторонним ножом. При внедрении ножа записывались диаграммы деформирования ткани, рассмотрев полученные диаграммы, были выделены основные стадии деформирования ткани и характерные точки с пиковой нагрузкой – рисунок 8: 1 – закрепление нити больше разрывной на- грузки; 2 – закрепление нити меньше разрывной нагрузки, имеет место вытягивание и раздвижка.

Участок I-II. Преодоление сил трения между системами нитей, в зависимости от степени закрепления нитей в ткани наблюдается два случая: 1) если силы трения между нитями велики, то происходит разрыв нитей (точка № 1']; 2) в обратном случае нити начинают вытягиваться и раздвигаться. На диаграмме наблюдается пиковая точка № 1.

Участок II-III. Происходит движение лезвия через образовавшееся отверстие, при этом также наблюдается два случая поведения ткани: 1) если силы трения между нитями велики, то режущая кромка ножа постепенно разрушает нити, 2) в обратном случае нити, смещаются друг относительно друга, не разрушаются, но оказывают сопротивление перемещению ножа за счет трения о них его режущей кромки. На диаграмме появляется пиковая точка № 2, положение которой обусловлено конструкцией индентора (длиной режущей части лезвия).

Отметим, что положение точки № 1, как и точки начала участка II-III, связано со степенью изгиба нитей в ткани, чем больше уработка какой либо из систем нитей, тем дальше в левую сторону будут смещаться данные точки. На рисунке 8 в качестве допущения приняты одинаковые уработки нитей для рассматриваемых случаев поведения ткани.

Установлено, что наибольшая нагрузка при прорезании ткани ножом (точка № 1'] наблюдается для полотняного переплетения, а наименьшая для рогожки 3/3, остальные переплетения показали промежуточные значения. Наибольшая нагрузка при движении лезвия через образовавшееся отверстие (точка № 2], которое

Таблица 2 – Показатели, характеризующие способность ткани сопротивляться внедрению ножа

Table 2 – Indicators characterizing the ability of the fabric to resist the introduction of a knife

Переплетение ткани	Пиковая нагрузка на участке I-II, Н		Пиковая нагрузка на участке II-III, Н		Деформация при разрушении, мм		Работа внедрения, Дж/г
Вдоль системы:	Осн.	Ут.	Осн.	Ут.	Осн.	Ут.	Осн.	Ут.
Полотняное	238,75	232,40	78,70	99,85	10,05	18,92	13,17	17,57
Рогожка 3/3	33,55	49,25	77,25	94,90	5,36	7,33	8,86	10,79
Репс уточный 3/3	101,45	62,50	91,95	143,55	6,49	4,85	12,42	16,84
Саржа 1/5	62,00	67,85	150,75	117,45	9,68	9,89	15,53	13,48
Саржа 3/3	83,75	63,15	140,70	93,70	7,03	6,83	15,76	12,22
Атлас шестиремизный	78,00	67,40	155,65	124,45	6,84	6,32	16,94	12,47

сопровождается вытягиванием и раздвижкой нитей, наблюдается для ткани переплетения атлас, а наименьшая для рогожки 3/3 и полотняного переплетения.

Наибольшая работа внедрения вдоль основы наблюдается для ткани переплетения атлас, а вдоль утка для полотняного переплетения. Самые низкие значения

Перемещение индентора, мм

Рисунок 8 – Общий вид диаграмм деформирования ткани при внедрении индентора в виде ножа Figure 8 – General view of tissue deformation diagrams during the introduction of an indenter in the form of a knife работы внедрения характерны для ткани переплетения рогожка 3/3. Стоит отметить, что для большинства образцов свойственна анизотропия работы деформирования в зависимости от направления нитей.

Таким образом, можно отметить, что, несмотря на различный характер деформирования образцов тканей их работа может совпадать, так в среднем работа деформирования для всех тканей кроме рогожки 3/3 составляет от 14 до 15,4 Дж/г.

На рисунке 9 показаны особенности разрушения ткани полотняного и саржевого переплетений. Из данных таблицы 2 и рисунка 9 видно, что в зависимости от переплетения нитей ткань по разному сопротивляется внедрению индентора. Так, в случае полотняного переплетения наблюдаются наивысшие значения пиковой нагрузки в точке № 1’, происходит массовый разрыв нитей, и после этого структура ткани перестает оказывать существенное сопротивление движению индентора, который разрезает нити своей кромкой. На участке II-III нагрузка остается практически постоянной. Для других видов переплетений характерна ситуация, когда лезвие достаточно легко проникает в ткань, раздвигая и вытягивая нити, но при его дальнейшем продвижении совершается работа по преодолению сил трения между не разрушенными нитями, наблюдается рост нагрузки до абсолютного максимума на участке II-III (точка № 2).

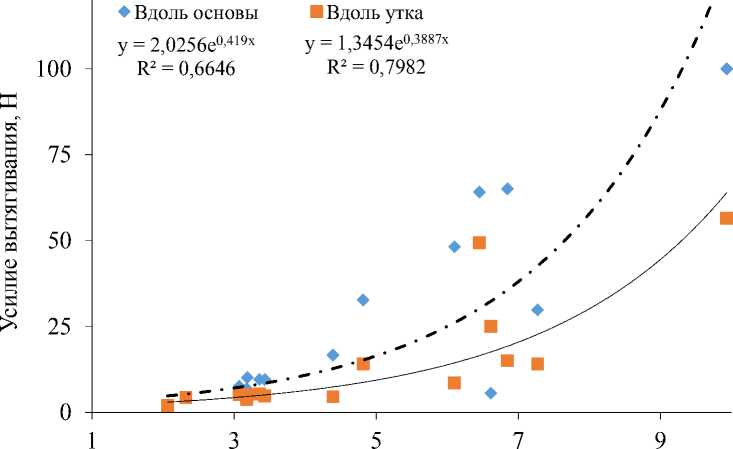
полотняное переплетение plain weave fabric саржевое переплетение twill fabric

Рисунок 9 – Внедрение ножа в арамидную ткань, выработанную различными переплетениями

Figure 9 – The introduction of the knife into the aramid fabric produced by various weaves

Очевидно, что степень закрепления нитей в ткани зависит от геометрических параметров ее строения, таких как высота волны изгиба нити, соотношение высот волн изгиба основы и утка, диаметров нитей в ткани с учетом смятия. В таблице 3 представлены значения высот волн изгиба основы и утка, размеры диаметров нитей по горизонтали с учетом смятия в ткани, а также значения усилий вытягивания и раздвигающей нагрузки систем нитей.

Геометрические параметры строения исследуемой арамидной ткани определялись на основе микросрезов вдоль основы и утка. Испытания по определению раздвигающей нагрузки проведены на приборе РТ-2 по ГОСТ 29104-91. Для определения усилия вытягивания использовалась соответствующая методика АО «ЦНИИСМ», в соответствие с которой с одного конца полоски ткани 25х250 мм делается бахрома длиной 50 мм, из бахромы выбирается 2 нити, так чтобы расстояние между ними и от краев образца было одинаковым. Свободный конец каждой нити заклеивают в клемму, состоящую из двух полосок плотной бумаги размером 40х7 мм. Испытания по вытягиванию двух нитей проводятся на разрывной машине Statigraph L фирмы Textechno, скорость нагружения 200 мм/мин.

Из данных таблицы 3 следует, что для образцов ткани полотняного переплетения и репса уточного 3/3 наблюдается ситуация, когда нити одной из систем имеют изгиб существенно больший, чем нити противоположной системы. В ткани полотняного переплетения основа имеет изгиб больше, чем уток, а в ткани репс уточный 3/3 наблюдается обратная ситуация. При этом для ткани полотняного переплетения характерно большее смятие нитей основы по горизонтали, а для репса уточного 3/3 – утка.

Построим зависимость усилия вытягивания нитей из различных арамидных тканей от коэффициента связности переплетения (рисунок 10). Коэффициент связности нитей в переплетении определяется по известной фор- муле:

_c = ^Po ^ Р у • ^T cp.

10 3 •F

,

где P_o и P_y – плотности ткани по основе и утку, нитей/ см; T - средняя линейная плотность основы и утка, текс; F – коэффициент переплетения, характеризующий степень его «рыхлости».

Коэффициент переплетения определяется по формуле:

F = 2 -R^ R_y ,            (19)

t o + t y

Таблица 3 – Значения показателей, характеризующих параметры строения и степень закрепления нитей в тканях различных структур

Table 3 – Values of indicators characterizing the parameters of the structure and the degree of fixation of threads in the tissues of various structures

Переплетение ткани	Диаметр нити в ткани, мм*		Высота изгиба нити, мм		ПФС	Усилие вытягивания нити, Н		Раздвигающая нагрузка, Н
Вдоль системы:	Осн.	Ут.	Осн.	Ут.	-	Осн.	Ут.	Осн.	Ут.
Полотняное	0,516	0,270	0,190	0,030	7,91	Более 100	56,52	Более 100	Более 100
Рогожка 3/3	0,350	0,341	0,136	0,163	4,64	6,89	3,78	14,4	13,7
Репс уточный 3/3	0,274	0,440	0,021	0,233	1,66	5,59	25,06	Более 100	16,7
Саржа 1/5	0,395	0,395	0,231	0,229	5,02	16,67	4,58	43,1	24,2
Саржа 3/3	0,406	0,412	0,137	0,151	4,81	9,56	4,82	27,2	22,3
Атлас шестиремизный	0,392	0,385	0,200	0,119	6,02	10,16	5,09	35,0	77,2

Примечание: * – диаметр нити с учетом горизонтального смятия.

где R_o и R_y – раппорт ткани по основе и утку; t_o и t_y – число связей по направлению основы и утка в раппорте переплетения, считается по вершинам связей.

Стоит обратить внимание на то, что коэффициент связности имеет ограниченную область использования, так как он не учитывает крутку нитей, их сырьевой состав и коэффициент трения, предполагает использование простых (главных, производных от главных, мелкоузорчатых) переплетений, примерное равенство соотношений плотностей нитей по основе и утку, и их линейных плотностей. Однако в рамках проводимого исследования эти допущения могут быть приняты.

Установлено, что с увеличением коэффициента связности наблюдается экспоненциальный рост усилия вытягивания нитей основы и утка из ткани. Полученный вывод вполне согласуется с данными по расчетным значениям силового взаимодействия нитей в местах их контакта.

В заключении необходимо ответить на вопрос о том, как влияют параметры строения ткани на характер ее деформирования при внедрении ножа. Итак, установлено, что для большинства рассмотренных структур защитных тканей наблюдается два случая деформирования при внедрении ножа.

Первый случай назовем «упругое разрушение», он наблюдается тогда, когда силы взаимодействия между нитями основы и утка слишком велики и происходит их массовый разрыв на начальном этапе внедрения индентора, а далее незначительная часть энергии затрачивается при трении индентора о края образовавшегося отверстия.

Второй случай назовем «вязкое разрушение», он наблюдается тогда, когда нити основы и утка имеют слабое закрепление в структуре ткани, на начальном этапе внедрения индентора нити начинают вытягиваться и раздвигаться, а не разрушаться, индентор легко образует входное отверстие, но по мере его продвижения затрачивается значительная часть энергии на вытягивание и раздвижку систем нитей.

Для того чтобы оценить какой случай деформирования ткани будет наблюдаться в каждом конкретном случае необходимо ввести понятие «степени упругости разрушения» – К_e .

Коэффициент связности

Рисунок 10 – Зависимость усилия вытягивания нитей от коэффициента связности переплетения Figure 10 – The dependence of the pulling force of the threads on the coefficient of connectivity of the weave

Определим степень упругости разрушения ткани при прорезании как отношение пиковой нагрузки на участке I-II к пиковой нагрузке на участке II-III. Если К_e < 1, а нагрузка в точке 2 больше нагрузки в точке 1, то разрушение ткани считается вязким, энергия будет затрачиваться в основном на вытягивание и раздвижку нитей. Если К_e > 1, а нагрузка в точке 1 больше нагрузки в точке 2, то разрушение ткани считается упругим, энергия будет затрачиваться в основном на разрыв нитей на начальном этапе внедрения, вытягивание и раздвижка затруднены из-за высокой степени закрепления нитей.

Вывод, важный с точки зрения проектирования тканей с заданным характером разрушения, заключается в том, что с приближением коэффициента связности к значению 5 коэффициент степени упругости разрушения становится больше 1 ( К_e > 1). Таким образом, для получения структуры ткани с максимальной прочностью при прорезании или проколе, необходимо получить коэффициент связности больший либо равный 5. Для структур, где необходимо реализовать «вязкое» разрушение (например, ткани для противоосколочной защиты) коэффициент связности переплетения должен быть меньше 5, а предпочтительно, находиться в пределах от 2 до 3,5.

Выводы

• 1)    практическая значимость работы заключается в том, что зная коэффициент связности ткани и параметры силового взаимодействия в месте пересечения основы и утка, становится возможным прогнозировать степень закрепления нитей в ткани и характер ее разрушения при взаимодействии с поражающим элементом;

• 2)    в рамках проведенной работы установлено, что ткань полотняного переплетения обладает наивысшей защитной способностью при прорезании ножом, это обусловлено монолитностью структуры ткани (достигнуты максимальные значения силы взаимодействия между нитями основы и утка), что позволяет исключить подвижность нитей;

• 3)    установлено, что разработанная ткань полотняного переплетения обладает анизотропией свойств в направлении основы и утка, которая возникает вследствие максимального изгиба основы и минимального изгиба утка, что не позволяет реализовать свойства систем нитей в одинаковой степени;

• 4)    установлено, что ткани переплетения саржа 3/3 и неправильный шестиремизный атлас имеют одинаковый изгиб основы и утка, удовлетворяют условию рав-нодеформативности, и тем самым имеют преимущества при изготовлении защитных изделий.