Исследование взаимосвязи толщины лесной подстилки и лесотаксационных характеристик с помощью методов машинного обучения

Лесная подстилка представляет собой напочвенное образование, формирующееся под пологом леса в результате ежегодного поступления на поверхность почвы продуктов опада, древесных остатков и отмерших мелких корней растений с последующим разложением органического вещества (минерализацией) [1–3]. Подстилка формирует перегнойно-аккумулятивный (дерновый) слой почвы, оказывает большое влияние на почвенные процессы и развитие леса, так как в ней накапливаются элементы питания растений, образуются перегнойные вещества, поступающие в нижележащие почвенные слои; она предохраняет почву от размыва (эрозии) и механического уплотнения. От мощности лесной подстилки, её состава, влажности, особенностей минерализации и гумификации органического вещества зависит плодородие, а также водно-воздушный режим лесных почв [3, 4]. Классификация лесных подстилок по функциональным признакам остаётся спорным вопросом. Одни исследователи рассматривают лесную подстилку как генетический горизонт лесных почв, а другие – как самостоятельное напочвенное образование в лесном биогеоценозе. В ряде работ показано, что лесная подстилка является одновременно подсистемой как почвенного покрова, так и фитоценоза (типа леса) [5]. Основатель лесной типологии В.Н. Сукачёв и авторитетные учёные в области лесного почвоведения, С.В. Зонн и Л.О. Карпачевский [6–8], считают подстилку особым, в определённой степени независимым, компонентом лесного биогеоценоза. В нашем исследовании лесная подстилка рассматривается также как компонент лесного фитоценоза, функционально связанный с условиями местопроизрастания, древесной породой и её таксационными характеристиками, живым напочвенным покровом. По нашему убеждению, созвучному с Т.М. Ильиной и А.П. Сапожниковым [9], свойства лесной подстилки определяются характеристиками древостоя и условиями местопроизрастания.

Основные характеристики лесной подстилки – мощность (толщина), плотность, состав и запас.

Мощность (толщина) лесной подстилки крайне изменчива. Она обусловлена составом и строением древостоя, связана с микрорельефом, зависит от богатства и влажности лесорастительных условий, принадлежности к типу леса и мозаичности живого напочвенного покрова [10, 11]. Предпринятые исследования поиска взаимосвязи лесной подстилки и таксационных характеристик древостоя выявили следующие закономерности. Толщина (мощность) лесной подстилки положительно связана с возрастом древостоя [12, 13]. В силу того что точность измерения толщины (мощности) подстилки относительно невысока, более надёжной характеристикой считается её запас [8, 14, 15]. Однако, как показывают результаты исследований, и этот показатель крайне вариативен в зависимости от географических условий, видового состава лесообразующих пород, возраста и ярусности насаждения, сомкнутости лесного полога, развития живого напочвенного покрова. Даже в опытах с многократной повторностью сбора образцов на пробных площадях в лесах европейской части России коэффициент вариации составляет более 0,4 [8, 14]. Запасы органического вещества в подстилке, как и её мощность, положительно связаны с возрастом древостоя: по мере его увеличения растёт количество опада и, соответственно, масса подстилки [8, 13, 16]. Возрастание доли хвойных пород в составе насаждений, продуцирующих плотный опад с затруднённой аэрацией, способствует снижению скорости его разложения и увеличению запасов подстилки [16]. В хвойно-широколиственных лесах выявлена отрицательная корреляция запаса подстилки с биомассой дождевых червей: увеличение биомассы червей приводит к снижению запаса органического вещества в подстилке из-за возрастания скорости разложения растительного опада [16]. Вместе с тем связь массы подстилки с наличием определённых древесных пород в составе насаждений неоднозначна. Одна и та же древесная порода в разных условиях может оказывать различное влияние на характер разложения лесной подстилки, так как процесс её формирования и трансформации зависит от взаимодействия многих факторов. По наблюдениям, лесная подстилка под одной и той же породой может состоять из растительных остатков разной степени разложения [4].

За рубежом показатели, характеризующие лесную подстилку, получают при масштабных работах по оценке почв в рамках национальных инвентаризаций лесов (НИЛ) или специальных проектов и программ. При ведении НИЛ в многолесных странах для определения характеристик подстилки осуществляют измерение её толщины (мощности), сбор образцов на пробных площадях, взвешивание в лабораторных условиях для определения объёмной плотности и химический анализ образцов [17]. Подобные измерения лесной подстилки выполняют в ходе почвенных обследований на подвыборке пробных площадей НИЛ США, Канады, Финляндии, Швеции [18–22]. В странах Европейского Союза и географически тяготеющих к ним данные о лесной подстилке и почвах собирают в рамках программы мониторинга лесов ICP-Forests1, в которой участвуют 42 страны2. Во многих странах мира из-за отсутствия системы мониторинга лесных почв данных о характеристиках лесной подстилки нет [23].

На практике на пробных площадях НИЛ сбор данных о подстилке для последующего определения запасов биомассы осуществляют методом разнообразных по форме шаблонов площадью около 0,5 м2. Отбор проб лесной подстилки сопровождается одновременным измерением её толщины. Количество отобранных образцов подстилки, как правило, не менее 10–15 на пробной площади. Отбор образцов для относительно мощной подстилки (более 5 см) проводится по слоям. Вся собранная биомасса хорошо перемешивается и взвешивается во влажном состоянии, затем, после высушивания в сушильном шкафу, в сухом – для определения условной плотности подстилки. После оценки массы лесной подстилки по слоям определённой мощности (см) рассчитывают уравнение регрессии зависимости мощности лесной подстилки и массы на единицу площади от условий местопроизрастания, лесотаксационных и климатических характеристик [24].

В нашей стране параметры лесной подстилки, как правило, оценивают при проведении натурных обследований почв и включают в описание почвенных разрезов [8, 25]. Фундаментальные и прикладные научные исследования лесных подстилок и их роли в биогеохимических процессах выполняют научные подразделения РАН, специализирующиеся на изучении почв: ФИЦ Почвенный институт имени В.В. Докучаева, Почвенный факультет МГУ имени М.В. Ломоносова, Институт биологии Коми НЦ УрО РАН, Институт физико-химических и биологических проблем почвоведения РАН (ИФХИБПП РАН), Институт леса Карельского научного центра РАН, Институт леса им. В.Н. Сукачева СО РАН, Центр по проблемам экологии продуктивности лесов РАН (ЦЭПЛ РАН) и другие [8, 10, 11, 26–34]. Несмотря на длительные углублённые исследования и усилия многих научных коллективов, в силу вариативности характеристик лесных подстилок при многообразии последних на территории страны, экспериментальных работ и аналитических обобщений для оценки параметров лесной подстилки и запасов органического вещества этого углеродного пула ещё крайне недостаточно.

Масштабные по территориальному охвату и методически однотипные измерения лесной подстилки выполняют на постоянных пробных площадях (ППП) государственной инвентаризации лесов (ГИЛ) [35]. Для этого за границей пробной площади делают одну прикопку глубиной 30–50 см. Устанавливают наличие или отсутствие лесной подстилки. При наличии лесной подстилки измеряют её мощность на прикопке. По мощности подстилку относят к одной из семи категорий интервальной шкалы: 0–1 см; 1,1–2,0; 2,1–3,0; 3,1–4,0; 4,1–5,0; 5,1–6,0 см; более 6,0 см. Помимо измерения толщины подстилки, устанавливают её тип согласно принятой в лесном почвоведении типологии: мор, модер, мулль. При последующей обработке в итоговых данных приводят распределение площади лесных земель объекта инвентаризации, занятой лесной подстилкой определённой мощности и определённого типа. Сводные результаты публикуют в составе Аналитического обзора по субъектам Российской Федерации (1- и 2-й циклы ГИЛ) или лесным районам (1-й цикл).

Цель исследования – поиск зависимости толщины лесной подстилки от лесотаксационных характеристик на подеревном уровне, соответствующем парцеллярному строению биогеоценоза, с использованием современных методов математического моделирования. Данные для моделирования собраны в ходе полевых работ. Полевые исследования в методическом плане схожи с практикой сбора образцов подстилки в ходе НИЛ зарубежных стран – выполнены в многократной повторности методом малых шаблонов (30^30 см в плане) на ППП ГИЛ. В нашем исследовании, в отличие от методики ГИЛ, мощность подстилки – не интервальная величина, а количественная мера в единицах (см). Полевые работы ограничены измерением толщины подстилки. Оценка плотности подстилки и содержания органического вещества не проводилась из-за отсутствия лабораторного оборудования для взвешивания и химического анализа образцов.

Рабочая гипотеза: мощность подстилки связана с древесной породой, т. е. с составом опада, зависит от богатства и влажности почв – принадлежности к определённому типу лесорастительных условий (ТЛУ), обусловлена вариативностью таксационных характеристик – возрастом деревьев, размером крон, высотой и диаметром деревьев. Мощность подстилки – недостаточно изученный параметр, точных методов измерений для него не существует, а оценки в ряде случаев субъективны [8, 14]. Для определения таких параметров предпочтительны регрессионные модели особого рода, включающие обучение на наборе переменных, отбор переменных по их вкладу в прогнозную модель, проверку модели на контрольной выборке и расчёт прогнозируемого показателя в результате реализации модели. Современные алгоритмы машинного обучения позволяют построить модели регрессионной зависимости параметров подстилки не только от количественных показателей, но и с учётом качественных, номинальных показателей: ТЛУ, класс бонитета, древесной породы. Важно заметить, что набор параметров, включаемых в модель, напрямую связан с пространственным уровнем моделирования. В нашем случае – это подеревный уровень учёта с соответствующими таксационными параметрами, т.е. парцеллярный уровень строения биогеоценоза. Моделирование на другом пространственном уровне, например повыдельном, предположительно может включать и другой набор параметров.

Материалы и методы исследования

Измерения толщины подстилки проведены на территории Валдайского района Новгородской обл. в 2024 г. на 13-ти ППП (рис. 1). На этих же ППП в ходе ГИЛ 2-го цикла производственной бригадой «Севзаплеспроект» филиала ФГБУ «Ро-слесинфорг» определены полевым измерительным комплексом (ПИК ГИЛ) таксационные показатели деревьев, а затем рассчитаны сводные, агрегированные по ППП. Подеревные и средние таксационные характеристики, а также координатная привязка ППП для нашего исследования предоставлены ФГБУ «Рослесинфорг». Координатная привязка ППП использована для создания пространственной основы с локализацией ППП и базы данных, включающей измеренные параметры подстилки, а также лесотаксационные показатели паспорта ППП, предусмотренные Регламентом ГИЛ 2-го цикла [35].

Обследованные ППП совмещены по координатам с типологическими единицами почв в стандартной классификации цифровой карты Почвенного института имени В.В. Докучаева и базой данных Единого государственного реестра почвенных ресурсов России3 [36]. Таким образом осуществлена привязка ППП к типам почв в стандартной классификации почвенной карты

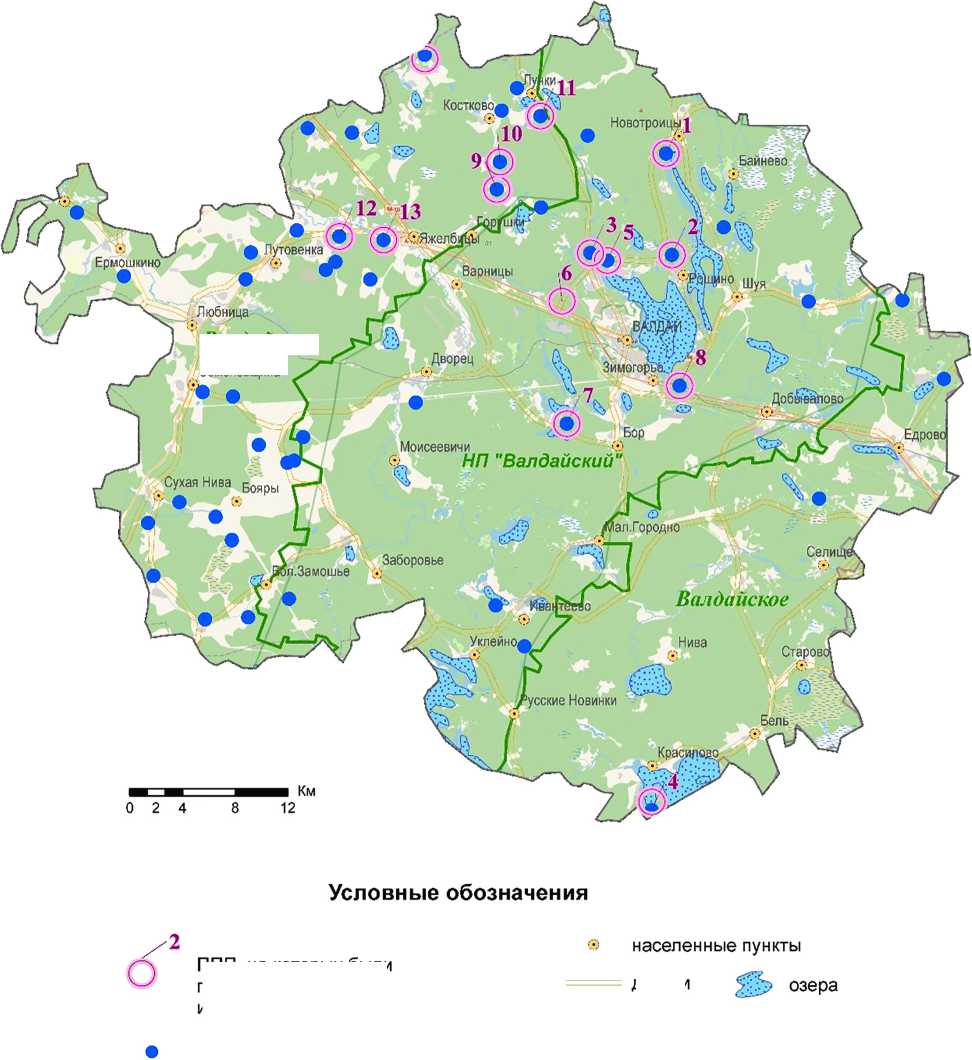
ППП 2 цикл ГИЛ

Валдайское

Семеновщина

ППП, на которых были проведены полевые измерения лесной подстилки

дороги ijJ административные границы

£^Р границы лесничеств и ООПТ

Рис. 1. Расположение ППП ГИЛ 2-го цикла с измеренными параметрами подстилки в ходе полевых работ. Валдайский район, Новгородская обл.

масштаба 1 : 2 500 000, что позволяет увязать измеренный параметр подстилки с распространёнными типологическими единицами почв на территории объекта работ. По принадлежности к типологическим единицам пять ППП приходятся на дерново-подзолистые иллювиально-железистые почвы, семь – на дерново-подзолистые преимущественно мелко- и неглубокоподзолистые и одна – на подзолы иллювиально-железистые (подзолы иллювиально малогумусовые) (рис. 2).

В границах обследованных ППП доминируют следующие древесные породы: сосна, ель, берёза, осина, лиственница (рис. 3).

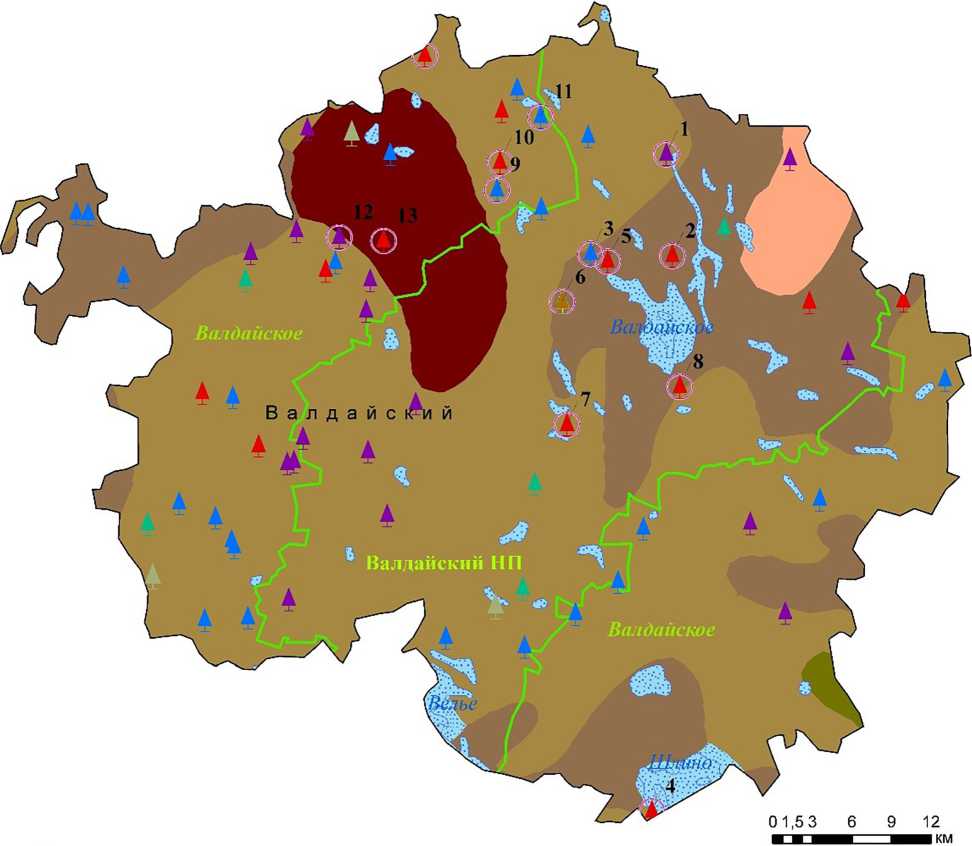
Почвы

(Единый государственный реестр почвенных ресурсов России)

Дерново-подзолистые преимущественно мелко- и неглубокоподзолистые f Дерново-подзолистые иллювиально-железистые

Дерново-подзолистые остаточно-карбонатные

| Подзолы иллювиально-железистые (подзолы иллювиально-малогумусовые)

[ Торфяные болотные верховые

Озера

Преобладающая порода на ППП

4 Сосна ,Т Лиственница А Осина

4 Ель    4 Береза           Ольха

ППП, на которых были проведены полевые измерения лесной подстилки границы лесничеств и ООПТ административные границы

Рис. 2. Геопривязка ППП к типам почв стандартной классификации цифровой почвенной карты масштаба 1 : 2 500 000. Валдайский район, Новгородская обл.

Классы бонитета представлены следующими категориями – Iб, Iа, I, II, III и IV. Наиболее репрезентативны измерения толщины подстилки в I и II классах бонитета – по 80 измерений (рис. 4).

В лесоучётных работах стандартно придерживаются классификации лесорастительных условий П.С. Погребняка [37, 38]. В нашем исследовании группы типов местообитаний по плодородию почвы – трофотопы – обозначены буквами латинского алфавита: A, B, C, D; для каждого из них на основе растительности напочвенного покрова выделено 6 типов увлажнения (гигрото-пов) – от сухих до очень влажных, обозначенных арабскими цифрами (0, 1, 2, 3, 4, 5). Объём выборки полевых измерений мощности подстилки с дифференциацией по типам лесорастительных условий (ТЛУ) проиллюстрирован рис. 5.

Наиболее представительная по объёму выборка из 120 измерений (шесть ППП) собрана для типа лесорастительных условий С2 – судубравы/ сурамени свежие (мезофильные). Заметим, что этот тип местообитаний наиболее характерен для лесов Валдайского района в целом. К ТЛУ В2 приурочено 60 измерений, 40 образцов собраны на ППП в ТЛУ А2 и по 20 – в С4 и А5.

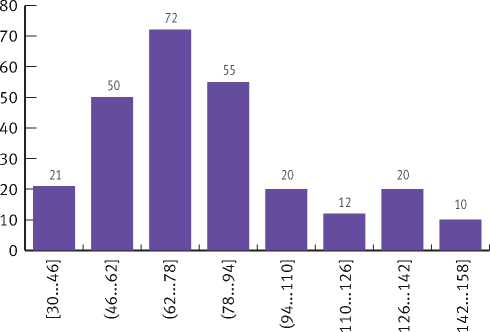
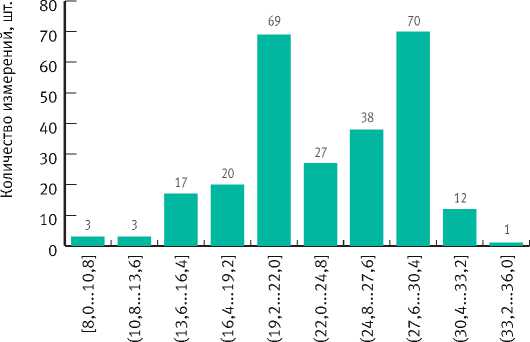
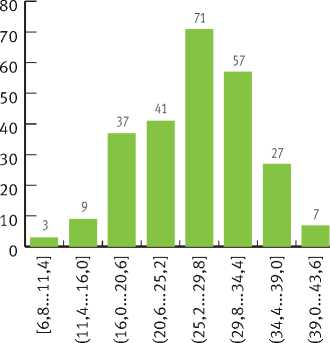
Возраст деревьев варьирует от 30 до 154 лет (в среднем – 79 лет), высота – от 8 до 33,7 м (в среднем – 23,9 м), диаметр на высоте 1,3 м – от 6,8 до 58,1 см (в среднем – 28,1 см), максимальный диаметр крон – от 1,8 до 11,6 м (в среднем – 4,4 м). Баланс выборочных измерений мощности подстилки по интервалам лесотаксационных показателей приведён на рис. 6.

В основу методики полевых измерений положены Методические рекомендации по определению запасов лесной подстилки при лесовод-ственных исследованиях [15]. Чтобы собрать достаточную по объёму выборку на ППП и исследовать вариации мощности лесной подстилки по площади ППП, исполнители отдали предпочтение «методу малых шаблонов». Этот способ считается статистически надёжным, так как на одной пробной площади отбирают достаточный объём образцов для её характеристики [8, 14].

Согласно Методическим рекомендациям ВНИИЛМ (1979), важно правильно организовать

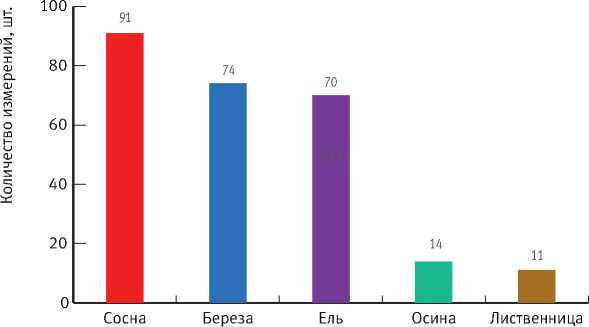
Рис. 3. Распределение числа выборочных измерений мощности подстилки по древесным породам

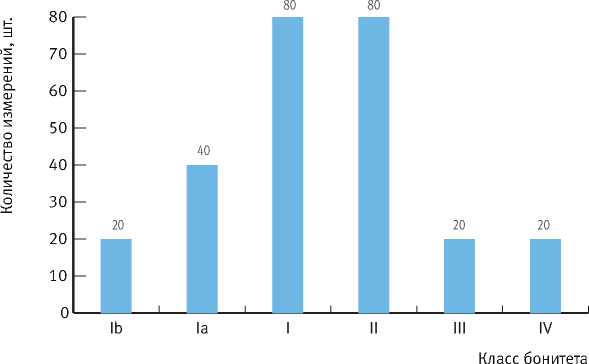
Рис. 4. Распределение числа выборочных измерений мощности подстилки по классам бонитета

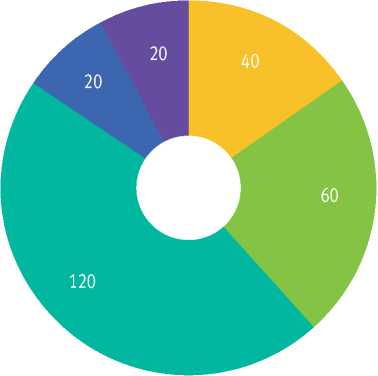
Рис. 5. Распределение числа выборочных измерений мощности подстилки по типам лесорастительных условий

а

б

Количество измерений, шт.                               Количество измерений, шт.

Диапазоны возраста, лет

Диапазоны высот, м

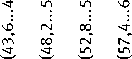
Дапазоны диаметра, см

Диапазоны диаметра крон, м

Рис. 6. Гистограмма частот выборочных измерений мощности подстилки с группировкой по диапазонам переменных: а ) возраст, лет; б ) высота, м; в ) диаметр на высоте 1,3 м, см; г) максимальный диаметр крон, м

отбор образцов в границах пробной площади. На пробной площади их нужно отбирать в 20-кратной повторности, в силу того что характеристики подстилки сильно варьируют. Такая повторность позволяет получить погрешность оценки параметров подстилки до ±10% [8, 14]. Для правильного отбора индивидуальных образцов подстилок рекомендуется располагать прикопки в пределах пробных площадей равномерно. На круговых пробных площадях – по двум перпендикулярным диаметрам через каждые 2,5–3,0 м. Согласно Регламенту ГИЛ, ППП представляет собой круг площадью 0,05 га и радиусом 12,62 м. Руководствуясь Методическими рекомендациями [15], исполнители закладывали 4 прикопки (пробы) от центра ППП в направлении на север (С) на расстоянии 3 м друг от друга. Далее по 4 прикопки в направлении на В, Ю, З. Еще 4 размещали в направлении на СВ, ЮЗ, ЮВ, СЗ у границ пробной площади. Таким образом, полевые замеры толщины подстилки выполняли на 20 прикопках, равномерно размещённых и охватывающих всю площадь ППП. Глубина прикопки – 30 см.

На прикопке отбирали образец подстилки по шаблону квадратной формы размером ~ 30x30 см. Шаблон накладывали на поверхность подстилки и вырезали по периметру. Мощность (толщину) слоя подстилки (в см)

измеряли от верхней «плоскости» до нижней границы подстилки, исключая листья, ветки и древесные остатки над основной плоскостью. Результаты измерений мощности подстилки заносили в полевую ведомость. В ведомости полевых описаний ППП указывали: расстояние прикопки от центра ППП, место расположения прикопки (между кронами деревьев или около ствола), древесную породу в месте расположения прикопки, фактические виды растительности живого напочвенного покрова, тип почвы по цифровой основе Почвенного института им. В.В. Докучаева и Единого государственного реестра почвенных ресурсов. Всего для статистической обработки на 13-ти ППП объем выборки составил 260 полевых измерений.

Для статистического анализа и построения моделей использованы полученные на прикопках данные по мощности (толщине) подстилки и лесотаксационные показатели на подеревном уровне, определённые с помощью полевого измерительного комплекса (ПИК) ГИЛ4 (рис. 7), а также качественные характеристики, внесённые в паспорт ППП: тип леса, тип лесорастительных условий, класс бонитета и древесная порода.

Зависимая (целевая) переменная в моделях – мощность подстилки (толщина), независимые переменные – ТЛУ, древесная порода, класс бонитета, высота, возраст древесной породы, максимальная ширина кроны древесной породы, диаметр ствола древесной породы на высоте 1,3 м.

Массив собранных данных обработан для получения стандартных описательных статистик. Для поиска связи целевой (зависимой) переменной – мощности подстилки – с лесотаксационными показателями использованы

а

б

Рис. 7. Маркировка деревьев на ППП ( а ) и измерение таксационных характеристик ПИК ГИЛ (б)

наиболее типичные алгоритмы машинного обучения. Экспериментально опробовано 7 таких алгоритмов: нейросетевая регрессия, регуляризованная линейная регрессия, регрессия методом бустинга, метод дерева решений, метод случайного леса (Random Forest), метод опорных векторов и метод K-ближайших соседей. Расчёт статистических характеристик и моделирование выполнены в программном пакете с открытым исходным кодом JASP версия 0.18.3 [39].

Задача моделей машинного обучения – прогноз целевого показателя на основе набора входных переменных. Алгоритм машинного обучения реализуется поэтапно: 1) обучение модели на выборке определённого объема; 2) выбор модели для прогнозирования целевого показателя; 3) тестирование модели на независимой выборке. На заключительном этапе исследователь отбирает адекватную модель по метрикам её качества и интерпретирует. Для отбора оптимальной модели использованы следующие критерии (метрики) качества, типичные для регрессионного анализа5, реализованного в машинном обучении [40]:

/ средняя абсолютная ошибка (Mean Absolute Error – MAE);

^ средний квадрат отклонения, или среднеквадратическая ошибка (Mean Squared Error – MSE);

^ корень квадратный из среднеквадратической ошибки, имеющий размерность исходных данных (RMSE);

^ средняя абсолютная ошибка/средний модуль отклонения (Mean Absolute Error – MAE / Mean Absolute Deviation – MAD) (MAE/MAD);

^ относительная ошибка на объектах оценки или средний процент отклонения, % (Mean Absolute Percent Error – MAPE);

^ коэффициент детерминации - доля дисперсии, объяснённая моделью в общей дисперсии целевой переменной ( R ²).

Описание опробованных алгоритмов можно найти в специальной литературе [40, 41].

Основное условие использования регрессионных моделей в машинном обучении – непрерывность целевого показателя – в нашем исследовании соблюдена.

Результаты моделирования мощности подстилки и обсуждение

Статистический анализ данных полевых измерений

На начальном этапе, предваряющем моделирование, целесообразно вычислить описательные статистики целевой (зависимой) переменной (табл. 1).

Таблица 1. Сводные статистические характеристики толщины (мощности) подстилки по итогам полевых работ. Валдайский район, Новгородская обл.

Описательная статистика           Значение

Объём выборки	260
Медиана	2,00
Медианное абсолютное отклонение (MAD)*	1,00
Робастное медианное абсолютное отклонение (MAD)	1,48
Межквартильный размах (IQR)**	2,50
Среднее	2,98
Стандартное отклонение	2,52
Дисперсия	6,32
Асимметрия	1,82
Эксцесс	3,09
Коэффициент вариации	0,84
Минимум	0,50
Максимум	12,00

*Аналог стандартного отклонения для медианы.

**Аналог дисперсии для медианы.

Нужно заметить, что статистический ряд целевой переменной не подчиняется закону нормального распределения. Асимметрия положительная. В таком случае усреднённую величину показателя характеризует медиана. Медиана в сочетании с медианным абсолютным отклонением (MAD) и межквартильным размахом (IQR) считается оптимальной оценкой статистического ряда при небольшом объёме выборки и наличии выбросов данных [42, 43]. Медианное абсолютное отклонение является аналогом стандартного отклонения среднего, а межквартильный размах – аналогом дисперсии для медианы, статистически надёжным и устойчивым к выбросам данных. Малое значение межквартильного размаха предполагает, что данные согласованы, большое – свидетельствует о большом разбросе данных и их высокой изменчивости. Результаты статистического анализа измеренной мощности (толщины) подстилки на ППП показывают, что в среднем толщина лесной подстилки (медиана) составляет 2,0±1,0 см (см. табл. 1). Показатель существенно варьирует: коэффициент вариации – 0,84, что свидетельствует о неоднородности выборки.

Разнообразие лесной подстилки по мощности связывают с различиями лесорастительных условий – богатством и влажностью почв [8, 14, 44], а в границах обследуемой площади – с изменчивостью влажности, микрорельефом, местоположением отобранного образца (расположение у ствола (под кроной) или в межкроновом пространстве) [14]. Для поиска связи характеристик подстилки с типами лесорастительных условий выполнена группировка ППП с отобранными образцами лесной подстилки по ТЛУ. Сводные статистические показатели мощности подстилки с группировкой по ТЛУ приведены в табл. 2. Напомним, что усреднённую величину мощности характеризует медиана.

Наибольшая по мощности лесная подстилка чаще встречается в борах ультрагигрофильных (мокрых) А5 – 10,0±1,0 см, далее в порядке убывания мощности: боры свежие (мезофильные) А2 – 4,0±1,5 см; субори свежие (мезофильные) В2 – 2,0±1,0 см и судубравы/сурамени свежие (мезофильные) С2 – 2,0±1,0 см; судубравы/су-рамени сырые (гигрофильные) С4 – 1,25±0,5 см (см. табл. 2). Группировка выборочных измерений по ТЛУ существенно снизила коэффициент вариации мощности: с 0,84 в общей выборке по 260 измерениям (см. табл. 1) до 0,21–0,56 с группировкой по ТЛУ (см. табл. 2).

Таблица 2. Мощность подстилки, см, с группировкой по ТЛУ по результатам обследования 13-ти ППП.

Сводные статистические характеристики. Валдайский район, Новгородская обл.

Описательная статистика	Мощность подстилки, см
	Тип лесорастительных условий
	A 2	B 2	C 2	С 4	A 5
Объём выборки	40	60	120	20	20
Медиана	4,0	2,0	2,0	1,25	10,0
Медианное абсолютное отклонение*	1,5	1,0	1,0	0,5	1,0
Межквартильный размах**	2,5	1,5	1,5	1,0	2,3
Среднее	4,60	2,25	1,95	1,43	9,65
Стандартная ошибка среднего	±0,27	±0,18	±0,09	±0,18	±0,46
Стандартное отклонение	1,70	1,14	1,09	0,78	2,06
Дисперсия	2,90	1,29	1,18	0,61	4,24
Асимметрия	0,25	0,67	0,96	0,73	-1,32
Эксцесс	-0,42	0,22	0,95	-0,23	1,52
Коэффициент вариации	0,37	0,55	0,56	0,55	0,21

*Аналог стандартного отклонения для медианы.

**Аналог дисперсии для медианы.

Таблица 3. Мощность подстилки, см, в зависимости от местоположения пробы – в межкроновом пространстве или у ствола дерева – с группировкой переменных по группам пород. ТЛУ С₂. Валдайский район, Новгородская обл.

Статистический показатель	Группа древесных пород
	Хвойные		Лиственные
	Мощность подстилки в зависимости от местоположения
	межкроновое пространство	у ствола	межкроновое пространство	у ствола
Объём выборки	39	23	37	21
Медиана	2,5	2,5	1,0	1,0
Медианное абсолютное отклонение*	0,5	0,5	0,0	0,5
Межквартильный размах**	1,0	1,3	0,5	0,5
Среднее	2,6	2,8	1,2	1,2
Стандартное отклонение	0,7	1,2	0,6	0,6
Дисперсия	0,6	1,4	0,4	0,4
Асимметрия	0,49	1,34	2,8	1,3
Эксцесс	-0,49	1,21	11,7	2,6
Коэффициент вариации	0,29	0,41	0,54	0,50

*Аналог стандартного отклонения для медианы.

**Аналог дисперсии для медианы.

В ходе стационарных наблюдений за мощностью подстилки выявлена следующая закономерность её распределения по площади пробы: максимум накопления – у ствола (под кроной) и минимум – в межкроновом пространстве или на границе крон [8]. Эта закономерность подтверждена недавними исследованиями в Волжско-Камском заповеднике, где в приствольной зоне сосны и липы запасы в среднем 1,3–2,3 раза выше, чем в межкроновой зоне [13]. Логично предположить, что такая закономерность будет наблюдаться в более сложной комбинации, обусловленной составом пород, и, как следствие, разнообразием опада и условий для его разложения (минерализации), опосредованно диагностируемых по ТЛУ (табл. 3). Наибольший объём выборки (120 измерений) приходится на характерный для объекта полевых работ ТЛУ – С2. В составе древесных пород этого ТЛУ доминируют ель, сосна, берёза и осина. Измерения мощности подстилки у ствола (под кроной) и в межкроновом пространстве по древесным породам не сбалансированы по количеству наблюдений, т.е. выборки различаются по объёму. На примере

ТЛУ С2 рассмотрим описательные статистики по группам древесных пород: хвойным и лиственным (см. табл. 3).

Медианы толщины подстилки для групп древесных пород в зависимости от местоположения пробы в сходных ТЛУ не отличаются (см. табл. 3): у хвойных деревьев в межкроновом пространстве и у ствола – 2,5±0,5 см, у лиственных в межкроновом пространстве и у ствола – 1,0±0,5 см. Изменчивость отдельных значений относительно медианы (межквартильный размах) у хвойных деревьев больше у ствола – 1,3, в межкроновом пространстве – 1,0, а у лиственных одинакова – 0,5 у ствола и в межкроновом пространстве. Дальнейший поиск различий мощности подстилки в зависимости от местоположения на площади пробы с помощью непараметрических критериев корреляции теряет смысл.

Гипотеза о том, что в приствольной части мощность подстилки больше, чем в межкроновом пространстве, не подтверждена нашими исследованиями. Возможно, для более основательного суждения об изменчивости мощности подстилки по мере удаления от ствола к периферии требуется сбалансированная выборка большего объёма с широким спектром ТЛУ и древесных пород, проведение многолетних наблюдений, поскольку мощность подстилки сильно варьирует не только в пространстве, но и в течение года и по годам. Амплитуда колебаний опада, связанная с погодными условиями в течение года и по годам, влияет на количество опада, скорость его разложения, мощность подстилки и её запас.

Распространено утверждение о связи характеристик подстилки с классификационными единицами почв и их характеристиками, которое сформировано на основе результатов полевых почвенных обследований по описаниям почвенных разрезов. Для поиска связи между мощностью подстилки и почв выполнена группировка измеренной мощности по видам почв: дерново-подзолистые преимущественно мелко-и неглубокоподзолистые (140 измерений) и дерново-подзолистые иллювиально-железистые (100 измерений). Для определения значимых различий между медианами двух выборок используем ранговый непараметрический U-критерий Манна Уитни (табл. 4).

Оценка различий мощности подстилки по видам почв по критерию Манна Уитни показывает, что различия в группах имеют случайный характер и статистически недостоверны. Медианы мощности для обоих видов почв не различаются – 2,0±1,0. Критерий Манна Уитни существенно выше критического значения (0,173) при уровне доверительной вероятности 0,95. Ранговая бисериальная корреляция, как мера величины различий, мала – -0,102. Различия, если и есть, то настолько невелики, что не имеют практического значения. Несмотря на ограниченный набор экспериментальных данных в выборках, наши исследования опровергают вероятность статистически значимых различий мощности подстилки по видам почв.

Результаты математического моделирования зависимости мощности подстилки от лесотаксационных характеристик на подеревном уровне (уровне парцелл)

Характеристики лесной подстилки недостаточно изучены, они крайне вариативны, закономерности и взаимосвязи с компонентами биогеоценоза, как правило, установлены по выборочным

Таблица 4. Распределение мощности подстилки и оценка статистически значимых различий мощности по видам почв. Валдайский район, Новгородская обл.

Описательная статистика	Мощность подстилки, см
	Вид почв
	дерново-подзолистые иллювиально-железистые	дерново-подзолистые преимущественно мелко- и неглубокоподзолистые
Объем выборки	100	140
Медиана	2,0	2,0
Медианное абсолютное отклонение*	1,0	1,0
Межквартильный размах**	2,0	3,0
Среднее	2,5	3,4
Стандартное отклонение	1,7	3,0
Коэффициент вариации	0,7	0,9
Критерий Манна Уитни	6 283,0
Ранговая бисериальная корреляция	-0,102

*Аналог стандартного отклонения для медианы.

**Аналог дисперсии для медианы.

измерениям недостаточного объёма. Для статистического анализа трудно сформировать сбалансированную выборку по компонентам биогеоценоза и таксационным показателям фитоценоза. Точных методов измерений для ряда параметров подстилки, в частности её мощности, не существует, или они не поддаются стандартизации. Свойства подстилки крайне вариативны в пространстве и во времени – по сезонам года и годам. Концептуальные построения относительно того, считать ли подстилку независимым компонентом фитоценоза или генетическим подгоризонтом почв, противоречивы и нечётко сформулированы. Данные полевых измерений содержат экстремумы, и стандартные параметрические методы не годятся для оценки таких переменных. В подобных ситуациях прибегают к использованию экспертных систем и методов машинного обучения.

В отличие от традиционных статистических процедур, регрессия строится ансамблем моделей, которые пошагово «приспосабливаются» к данным, т.е. на каждой последующей итерации модель исправляет ошибки предыдущей [40, 41, 45].

В нашем исследовании для моделирования мощности лесной подстилки опробованы следующие алгоритмы машинного обучения: нейросетевая регрессия, регуляризованная линейная регрессия, регрессия методом бустинга, методом дерева решений, методом случайного леса (Random Forest), методом опорных векторов и методом K-ближайших соседей (табл. 5). Во всех экспериментах модель обучалась (train) на выборке из 166 измерений, отбиралась для моделирования переменной (validation) по выборке из 42 измерений, оценивалась (test) на части выборки из 54 измерений.

Таблица 5. Результаты моделирования мощности подстилки с помощью алгоритмов машинного обучения. Валдайский район, Новгородская обл.

Модель	Критерий качества модели		Значимость отдельных	Ранжирование	Ранг модели по
	Критерий	Значение	признаков в модели	признаков по значимости, %	набору критериев качества
Регрессия методом бустинга	MSE	2,31	ТЛУ	46,3	4
	MSE (scaled)	0,21	Возраст	25,1
	RMSE	1,52	Древесная порода	23,5
	MAE / MAD	1,10	Класс бонитета	3,5
	MAPE	36,30	Высота	1,1
	R2	0,79	Максимальная ширина кроны	0,5
			Диаметр*	0,0
Регрессия методом дерева решений	MSE	0,60	Класс бонитета	43,5	2
	MSE (scaled)	0,12	Возраст	32,9
	RMSE	0,77	Древесная порода	9,6
	MAE / MAD	0,60	Высота	8,3
	MAPE	34,20	Диаметр*	2,7
	R2	0,89	ТЛУ	1,8
			Максимальная ширина кроны	1,2
Нейросетевая регрессия	MSE	0,90	Максимальная ширина кроны	23,0	2
	MSE (scaled)	0,10	Диаметр*	22,0
	RMSE	0,95	Высота	20,0
	MAE / MAD	0,73	Класс бонитета	18,0
	MAPE	34,40	Возраст	17,0
	R2	0,90	Без древесной породы и ТЛУ	-

Окончание табл. 5

Модель	Критерий качества модели		Значимость отдельных	Ранжирование	Ранг модели по
	Критерий	Значение	признаков в модели	признаков по значимости, %	набору критериев качества
Регрессия методом случайного леса	MSE	1,68	ТЛУ	27,0	3
	MSE (scaled)	0,24	Древесная порода	22,1
	RMSE	1,30	Класс бонитета	19,4
	MAE / MAD	0,87	Возраст	10,9
	MAPE	29,72	Диаметр	8,4
	R2	0,77	Максимальная ширина кроны	7,4
			Высота	4,8
Регуляризованная линейная регрессия	MSE	2,20	ТЛУ	20,0	5
	MSE (scaled)	0,42	Высота	19,0
	RMSE	1,49	Возраст	18,0
	MAE / MAD	1,11	Диаметр	16,0
	MAPE	36,40	Класс бонитета	14,0
	R2	0,62	Максимальная ширина кроны	13,0
			Без древесной породы	-
Регрессия методом опорных векторов	MSE	1,15	Древесная порода	16,9	1
	MSE (scaled)	0,14	ТЛУ	16,3
	RMSE	1,07	Класс бонитета	15,1
	MAE / MAD	0,76	Высота	14,0
	MAPE	29,70	Возраст	13,5
	R2	0,86	Диаметр	12,3
			Максимальная ширина кроны	11,9
Регрессия методом K-ближайших соседей	MSE	0,94	Возраст	16,5	1
	MSE (scaled)	0,15	Высота	16,1
	RMSE	0,97	Диаметр	15,2
	MAE / MAD	0,61	Древесная порода	14,9
	MAPE	21,95	ТЛУ	13,3
	R2	0,85	Максимальная ширина кроны	12,4
			Класс бонитета	11,6

*Диаметр на высоте 1,3 м.

Нужно заметить, что некоторые из использованных нами алгоритмов, например такие, как нейросетевая и регуляризированная линейная регрессия, работают только с количественными переменными. В этом случае в модель включена опосредованная количественная характеристика класса бонитета [46] по таблицам хода роста [47] – средняя высота древесной породы в возрасте спелости, для хвойных пород – в возрасте 100 лет, для лиственных – 50 лет.

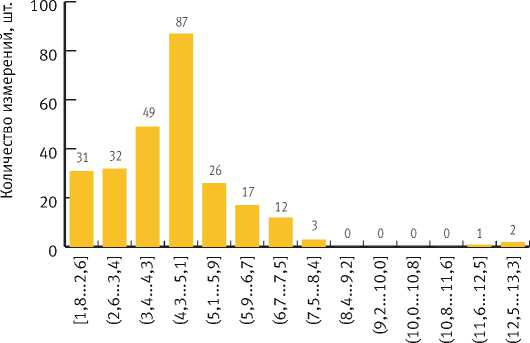
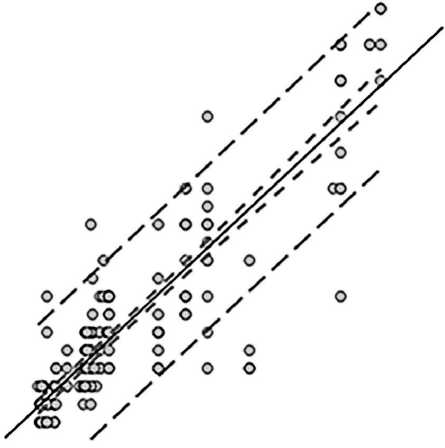
Выбор оптимальной модели для прогнозирования мощности подстилки проводился по набору метрик (критериев) качества модели и коэффициенту детерминации (R2). Коэффициент детерминации показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Модели с коэффициентом детерминации больше 0,8 считают хорошими [42, 43]. По величине коэффициента детерминации (R2) наилучшей моделью можно считать нейросетевую (0,90), далее следуют регрессия методом опорных векторов (0,86) и регрессия методом K-ближайших соседей (0,85) (см. табл. 5).

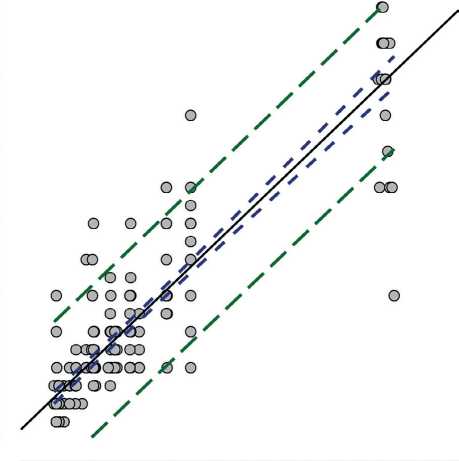
По набору метрик качества модели – ошибок опробования модели на тестовой выборке, в частности минимальной относительной ошибке прогнозирования моделью целевой переменной (средний процент отклонения – MAPE) (см. табл. 5), – наилучшей можно признать регрессию методом K-ближайших соседей ≈22%, регрессии методом опорных векторов и методом «случайного леса» дают отклонение модели в среднем – 29,7% каждая. Считая метрики качества и коэффициент детерминации равнозначными для оценки прогнозирования целевой переменной, модели ранжированы по эффективности от 1 – оптимальные модели до 5 – менее эффективные (см. табл. 5). По эффективности модели распределились в такой последовательности: 1) регрессия методом K-ближайших соседей и методом опорных векторов, 2) регрессия методом дерева решений и нейросетевая регрессия, 3) регрессия методом «случайного леса»; 4) регрессия методом бустинга и 5) регуляризованная линейная регрессия. Наиболее эффективные по метрикам качества и коэффициенту детерминации модели позволяют получить устойчивые прогнозные значения мощности подстилки по таксационным характеристикам, не смещённые и с приемлемой ошибкой при уровне доверительной вероятности 0,95 (рис. 8).

Рассчитанный наиболее эффективной моделью K-ближайших соседей показатель мощности подстилки соотнесён по координатам с местоположением образцов в границах ППП. Методами геостатистического моделирования в программной среде ГИС выполнена пространственная интерполяция модельных значений показателя для разных ТЛУ (рис. 9). Пространственная модель наглядно показывает изменчивость мощности подстилки в границах ППП, отнесённых к разным ТЛУ – B2, A2, С2 и A5. Основным фактором, обусловливающим изменчивость, служит микрорельеф.

Сходные модели для описания характеристик подстилки, построенные методами машинного обучения на выборках различного объёма, рассмотрены в работах [23, 48]. В работе [24]

а

б

Фактическая толщина подстилки, см

(-----------------JJJJJJ

0246810 12

Смоделированная толщина подстилки, см

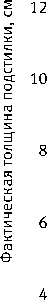
810      12

Смоделированная толщина подстилки, см

Рис. 8. Толщина подстилки, рассчитанная регрессионными моделями, методом К -ближайших соседей ( а ) и методом опорных векторов ( б ), и её соответствие фактическим измерениям

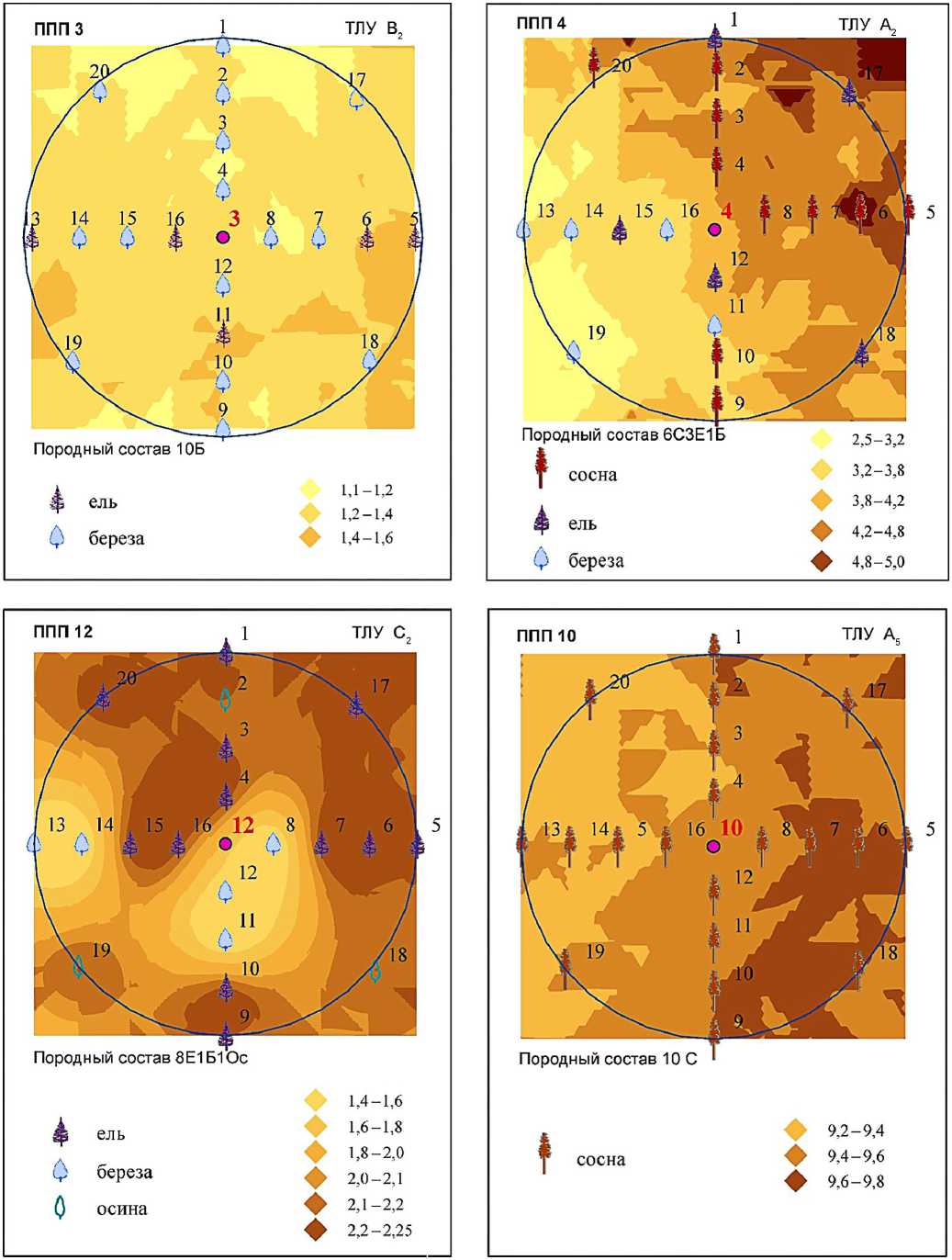
Рис. 9. Пространственная интерполяция прогнозного показателя – мощности подстилки, рассчитанного регрессионной моделью методом К-ближайших соседей для оценки запаса углерода в лесной подстилке по данным НИЛ на национальном уровне наиболее эффективной признана регрессионная модель методом случайного леса. В другом исследовании для моделирования углеродных параметров лесных экосистем, в частности запаса в лесной подстилке, отдано предпочтение методу K-ближайших соседей [48].

Выводы

По выборке полевых измерений мощности подстилки объёмом 260 образцов проверены рабочие гипотезы связи:

/ с типами лесорастительных условий (местообитаний);

^ с местоположением в пристволовой части деревьев или межкроновом пространстве для сходных по богатству и влажности почв условий местопроизрастания и доминирующих древесных пород, т.е. с учётом парцеллярной структуры фитоценоза;

^ с наиболее распространёнными видами почв.

Установлены различия средней мощности подстилки по типам лесорастительных условий, представленным на объекте полевых работ. Для более основательного суждения требуется выборка б о льшего объёма с б о льшим набором ТЛУ.

На примере наиболее представительного ТЛУ С2 – судубравы/сурамени свежие (мезофильные) – проверена гипотеза о связи мощности подстилки с её местоположением – в приствольной части или в межкроновом пространстве деревьев – по группам древесных пород (хвойным и лиственным). Гипотеза о том, что в приствольной части мощность и запас подстилки больше, чем в межкроновом пространстве, нашими исследованиями не подтверждена.

Статистическая оценка различий мощности подстилки по наиболее представительным на объекте исследований видам почв – дерново-подзолистым иллювиально-железистым и дерново-подзолистым преимущественно мелко- и неглубокоподзолистым – показала, что различия мощности носят случайный характер и статистически недостоверны. Проведённые исследования опровергают вероятность статистически значимых различий мощности подстилки по видам почв, различающихся по интенсивности проявления почвообразовательного подзолистого процесса.

Подтверждена гипотеза о связи мощности подстилки с таксационными характеристиками на подеревном уровне, соответствующем парцеллярному строению биогеоценоза. Алгоритмы машинного обучения дают хорошие результаты моделирования мощности подстилки с помощью регрессионной модели по набору количественных и качественных показателей: тип лесорастительных условий, древесная порода, класс бонитета, высота, возраст древесной породы, максимальная ширина кроны дерева, диаметр ствола на высоте 1,3 м. Оптимальными, исходя из совокупности критериев качества и коэффициента детерминации, оказались модели, построенные методом K-ближайших соседей и методом опорных векторов. Доля дисперсии, объяснённая моделями, в общей дисперсии целевой переменной составляет ≈ 0,86, а ошибка прогнозирования мощности подстилки – от 22 (K-ближайших соседей) до 29% (метод опорных векторов).

Обнадёживающие результаты проведённого исследования продемонстрировали эффективность использования методов машинного обучения для построения моделей показателей, для которых не существует точных методов измерения и отличающихся крайней вариативностью в пространстве и во времени.