Исследование задачи кручения упругих тонкостенных стержней с помощью метода интерполяции по коэффициенту формы области

Ранее были разработаны различные приближенные методы расчета призматических тонкостенных стержней на кручение. Среди них можно отметить работы Гулканяна Н.О., Канторовича Л.В., Мительмана Л.М., Лейбензона Л.С. [1-4] и др. В этих работах даны различные приближенные формулы для определения жесткости при кручении стержня. Рассмотрим известное решение задачи кручения тонкостенного призматического стержня произвольного сечения, данное Н.Х. Арутюняном [5]:

4 Q 2

I _к

ds

∫

Г h ( s )

где Q - площадь области, ограниченной средней линией г поперечного сечения, h ( s ) -толщина сечения h как функция переменной s , s – координата, отсчитываемая вдоль дуги средней линии сечения Г от некоторой ее точки (рис. 1).

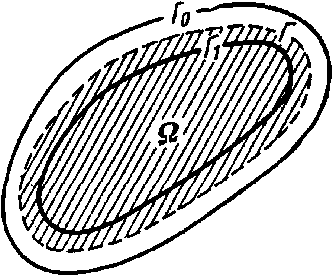
Рисунок 1 – Поперечное сечение произвольного тонкостенного стержня

Для тонкостенных стержней с одинаковой толщиной стенки ( δ = const) уравнение (1) принимает простой вид:

4⋅А02⋅δ

Iк =

L 0

где, для рассматриваемого нами случая, A 0 - площадь фигуры, ограниченной замкнутой линией L₀ , проведенной посредине стенки сечения; δ – толщина стенки сечения.

Преобразуем выражение (2) следующим образом:

I _к

4⋅А0 ⋅δ  L0  4⋅A0   2   2  L0  4⋅A02

=     ⋅         ⋅L ⋅δ =     ⋅⋅

L0      δ   L40    0 δ

где A ≈ L0 ⋅ δ - площадь поперечного сечения тонкостенного стержня. С учетом этого соотношения приведенная геометрическая жесткость кручения ( iк = Ак2 ) будет определяться по

формуле:

iк = δ

4 ⋅ A 0² _⋅

.

В работе [6] представлена зависимость поперечного сечения стержня :

коэффициента формы от площади и периметра

Kf

L 0

^, 2 ⋅ A 0

(5),

которое обращается в равенство для многоугольников, все стороны которых касаются вписанной окружности.

Подставляя неравенство (5) в уравнение (4), получим :

L 1 i ≥ ⁰ ⋅        .

k _{δ K} 2 _f

Рассмотрим вопросы, связанные с кручением тонкостенного стержня с сечение в виде прямоугольника (рис. 2).

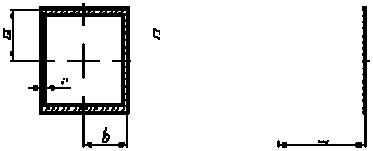
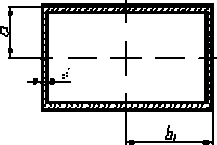
Рисунок 2 – Тонкостенный стержень с сечением в виде прямоугольника

Данные для некоторых сечений в виде тонкостенного прямоугольника представлены в таблице 1.

Таблица 1 – Значения приведенной геометрической жесткости для сечений в виде тонкостенных стержней с сечением в виде прямоугольников

Характеристика сечения	a/b=1	a/b=2	a/b=3	a/b=4
K f	8	10	13.333	17
1/ Kf	0.125	0.1	0.075	0.059
Ik , м 4	0.2	0.53	0.9	1.28
A , м 2	0.2	0.3	0.4	0.5
i k , (4)	5	5.926	5.625	5.12
ik , МКЭ	5.05	6.072	5.732	5.222
Разница , %	0.99	2.4	1.87	1.95

На основании данных, полученных методом конечных элементов (МКЭ), с помощью метода интерполяции по коэффициенту формы (МИКФ) получена аппроксимирующая функция, позволяющая получить значение приведенной геометрической жесткости при i < a / ь < 4 :

ik

3.886 + 473.209 ■

- 25513.223 ■

Kf k f J

Kf k f J

Данная зависимость помогает найти значение приведенной геометрической жесткости для любого соотношения сторон из указанного интервала.

Графическая иллюстрация полученной зависимости представлена на рисунке 3.

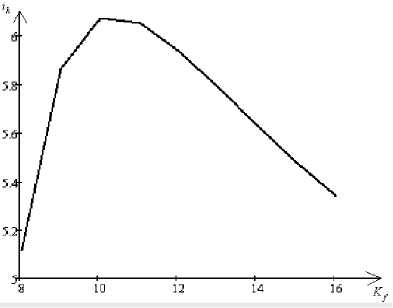
Рисунок 3 – Зависимость приведенной геометрической жесткости от величины коэффициента формы для сечений в виде тонкостенных прямоугольников

Оценим точность определения приведенной геометрической жесткости с помощью коэффициента формы (табл. 2).

Таблица 2 – Сравнение результатов , полученных с помощью коэффициента формы , с результатами , полученными МКЭ для сечений в виде тонкостенных прямоугольников

Характеристика сечения	a/b=1	a/b=2	a/b=3	a/b=4
K f	8	10	13.333	17
ik , (6)	5.022	5.879	5.678	5.222
i k , (7)	5.051	6.067	5.741	5.218
Разница , %	0.57	3.1	1.1	0.01

Полученная погрешность свидетельствует о высокой точности предложенного приема.

Похожие зависимости получаются при исследовании кручения тонкостенных стержней в виде эллипса.

Рассмотрим вопросы, связанные с кручением тонкостенного стержня с сечение в виде эллипса (рис. 4).

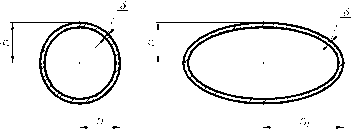
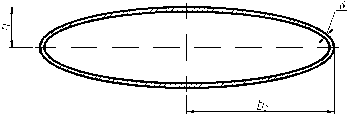
Рисунок 4 – Тонкостенный стержень с сечением в виде эллипса

Данные для некоторых сечений в виде тонкостенного эллипса представлены в таблице 3.

Таблица 3 – Значения приведенной геометрической жесткости для сечений в виде тонкостенных стержней с сечением в виде эллипсов

Характеристика сечения	a/b=1	a/b=2	a/b=3	a/b=4
K f	6.28	7.854	10.472	13.352
1/ Kf	0.1592	0.1273	0.095	0.0749
Ik , м 4	0.157	0.407	0.665	0.92
A , м 2	0.157	0.236	0.314	0.393
i k , (4)	6.366	7.34	6.734	5.968
ik , МКЭ	6.409	7.349	6.745	6.001
Разница, %	0.67	0.12	0.16	0.55

На основании данных, полученных МКЭ, с помощью МИКФ получена аппроксимирующая функция, позволяющая получить значение приведенной геометрической жесткости при i <  a / ь <  4 :

ik

4.23 + 382.83 ■

- 11715.706 ■

Kf k f J

Kf k f J

Данная зависимость помогает найти значение приведенной геометрической жесткости для любого соотношения осей из указанного интервала.

Графическая иллюстрация полученной зависимости представлена на рисунке 5.

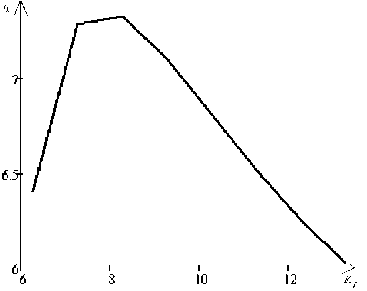
Рисунок 5 – Зависимость приведенной геометрической жесткости от величины коэффициента формы для тонкостенных эллипсов

Оценим точность определения приведенной геометрической жесткости с помощью коэффициента формы (табл. 4).

Таблица 4 – Сравнение результатов , полученных с помощью коэффициента формы , с результатами , полученными МКЭ для сечений в виде тонкостенных эллипсов

Характеристика сечения	a/b=1	a/b=2	a/b=3	a/b=4
K f	6.28	7.854	10.472	13.352
i k , (6)	6.403	7.324	6.779	6.054
i k , (8)	6.405	7.357	6.747	5.988
Разница , %	0.03	0.45	0.47	1.1

Полученная погрешность свидетельствует о высокой точности предложенного приема.

Отметим также, что при отношении a / b ≥ 4 , рассматриваемый профиль вырождается, и рассмотрение таких фигур осуществляется с помощью балочных функций.

Таким образом, предлагаемая методика позволяет перевести сложную математическую задачу в разряд инженерных при многовариантном проектировании.

Выводы

• 1.    Анализируя приведенные выше данные, можно отметить, что использование метода интерполяции по коэффициенту формы справедливо не только для односвязных, но и двусвязных областей. Ранее использование МИКФ к задачам такого рода не применялась .

• 2.    Использование МИКФ в задаче кручения, связанной с тонкостенной двусвязной областью, дает погрешность, не превышающую, в нашем случае, 3.2%, что свидетельствует о высокой точности предложенного приема и хороших перспективах использования МИКФ для подобных задач такого рода.